基于远离中心线的打点分布设计判异准则

闻学颖, 孙 维

(大连海洋大学 应用技术学院, 辽宁 大连 116300)

基于远离中心线的打点分布设计判异准则

闻学颖, 孙 维

(大连海洋大学 应用技术学院, 辽宁 大连 116300)

介绍了生产过程稳定与异常的基本概念,指出了稳定与异常的本质区别在于质量特性服从某一分布是否出现变化和控制图上是否呈现随机分布。异常的一种形式是样本打点超出控制限,这种情况的判异可由休哈特的著名判异准则“一点出限即判为异常”来解决;另一种形式的异常是样本打点没有超出控制限,但在控制域内呈现出单调排列、连续多个样本点上下交替变动以及样本点相对于中心线波动较大等打点分布不随机的现象。对于打点分布呈现出不随机的过程异常的判断问题,则选择相对于中心线波动较大的样本打点分布,设计相应的生产过程判异准则。

质量管理; 控制图; 判异准则; 设计

0 引 言

一般情况下,若一个生产过程中的质量特性是计量质量特性,则可以认为该质量特性是服从正态分布的[1]。如果在此过程中质量特性分布状况没有变化,就称该生产过程是处于可控制的稳定状态。

以X表示某稳定的生产过程中的计量质量特性,设X～N(μ,σ2),易知X具有取值偏向于μ附近的倾向,因此对于X的样本来说,必定是在X=μ附近一定范围内围绕X=μ随机分布的。否则意味着生产过程在一定程度上受到了系统因素的影响,可以认为生产过程出现了异常。

1 稳定与异常

根据统计原理建立控制图见图1,解决生产过程稳定与异常的判断[1-5]。控制图横轴表示样本序号,纵轴表示样本值。

1.1过程稳定

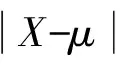
依据该判异准则,对一个打点出界即判为异常,则在逻辑上存在着误判的风险。即当X～N(μ,σ2)没有变化时,由于随机因素的影响,使得打点也可能出界。此时若按该准则判为异常,就是一种误判,其概率为0.002 7。这种误判是以真为假的误判,在数理统计上称为第1类错误。我们当然可以减小显著性水平使得出现以真为假的误判概率降低。但这却增大了所谓的以假为真误判的发生概率。对于后一种误判称为第2类错误。椐经验,按3σ原理构造的控制图,相应的两类错误造成的总损失最小,即α0=0.002 7是适宜的。

虽然控制图与假设检验的原理相同,但它们二者所选用的显著性水平的差异却是很大。假设检验选用的显著水平通常是控制图的几倍甚至几十倍。依据休哈特的“一点出界即判为异常”的判异准则,发生误判的机会增加了。为此通常把显著性水平取的相对小一些,尽管使犯第一类错误的概率大为降低,却导致犯第二类错误的机会增加,常常会出现鱼目混珠、漏发警报的现象。为此需要利用已建立的质量系统稳定或异常判断准则对控制图中打点的分布状况进行甄别[5],以便对质量过程的稳定与异常做出正确的判断。理论上说,样本的打点在控制图中的分布形式是多样的,判断系统异常的准则必定也是各异的。

1.2过程异常

如果一个生产过程中出现下列情况,即质量特性的样本打点要么超出控制限,要么于控制限内不是围绕中心线X=μ随机分布,则生产过程都是异常的。

2 过程异常判断准则的设计

2.1远离中心线打点的概率分布

设n个样本打点落在控制限内,且没有落在C区内,其分布如图1。样本打点分布有偏离均值的倾向,故应怀疑此控制图可能是系统因素作用的结果。

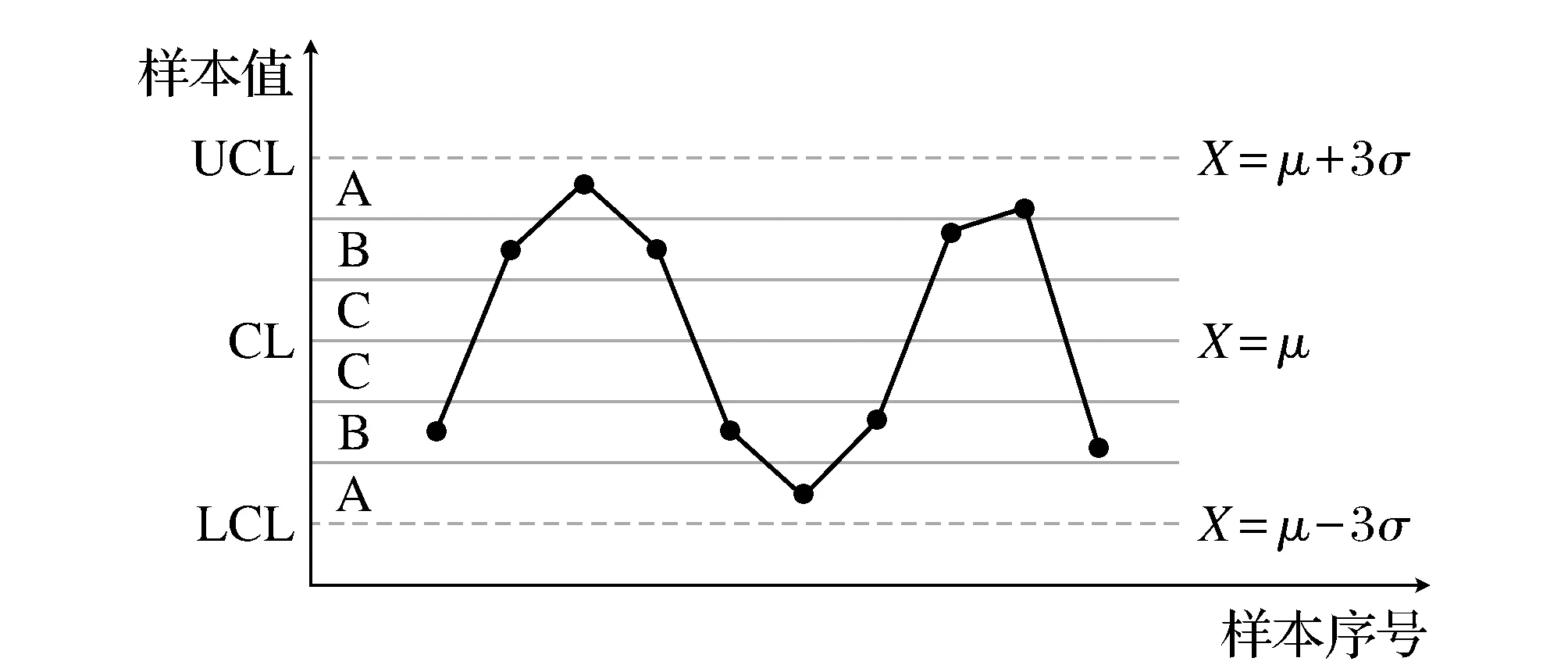
图1 控制图示例

设X～N(μ,σ2),打点落在A+B区域内概率为

现设有n个样本打点,其中有k个落在A+B区域内。那么k就服从以n,0.314 7为参数的二项分布[6],即k～B(n,0.314 7),记

P(n,k)=P(n个打点中有k个落在A+B内)

则有

严格意义上说,当n个样本打点限定落在控制限内,则n个样本打点落在A+B区域内的点数k便不再服从上述的二项分布。但由于X～N(μ,σ2),故打点落在控制限以外属小概率事件,因而可认为k～B(n,0.314 7),即仍有

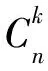
以Pn(k)表示“落在控制限内的n个打点中至少有k个位于A+B内”的概率,即

易知Pn(k)是k的减函数,且最小值为Pn(n)=P(n,n)=0.314 7n。

考虑到控制图的显著性水平α0=0.002 7,故有方程0.314 7n=0.002 7,解之n=5.115 8,取整n=5。现考虑从n=5开始,利用式(1),式(2)设计生产过程的判异准则。

2.2连续n个打点落在控制限内

当n=5,由式(1)可得

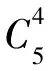
由于0.003 1与α0属同一数量级,而0.030 9过大,故得判异准则为:

准则1 若连续5个样本打点都落在控制限内的A+B内,则过程判为异常。

取n=6,由式(1)有

显然0.001 0过小,而0.011 7又偏大,故此时没有相应的判异准则存在。

当n=7,由式(1)计算可得

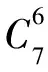
易知0.004 3与α0=0.002 7属同一数量级,由此可得设计判异准则为:

准则2 若连续7个样本打点中有6个打点落在A+B区域内,则过程判为异常。

当n=8,由式(2)计算可得

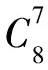
由于0.001 6与0.002 7处在同一数量级,故可以此来设计相应的判异准则。为此先考察9个点落在控制限内情况。

取n=9,由式(2)计算可得

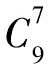
因为0.004 9与α0=0.002 7属同一数量级,故可取为判异准则的显著性水平,并依此得设计判异准则。但注意到事件“控制限域内连续8个点中至少有7个落在A+B内”发生必导致事件“控制域内9个点中至少有7个点落在A+B内”的发生,故只需按事件“控制域内连续9个点中至少有7个点落在A+B内”设计相应的判异准则即可。于是有

准则3 若连续9个样本打点中至少有7个打点落在A+B区域内,则过程判为异常。

当n=10,由式(2)得

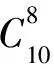
0.001 9与0.002 7属同一数量级,因此可设计相应的判异准则。

当n=11时,有

而0.004 7与0.002 7为同一数量级数值,故据此可设计判异准则。考虑到事件“连续10点中至少有8个落在A+B内”与事件“连续11点中至少有8点落在A+B内”的包含关系,即得。

准则4 若连续11个样本打点中至少有8个打点落在A+B区域内,则过程判为异常。

当n=12时,得

0.001 9与0.002 7属同一数量级,因此得设计判异准则为

准则5 若连续12个样本打点中至少有9个打点落在A+B区域内,则过程判为异常。

3 结 语

1) 继续令n取13,14,…,则还可能设计出新的判异准则。虽然如此,由于增大样本点数往往会加大具体操作时的难度,故一般并不选择较大的n来设计判异准则。

2) 在推导P(n,k)时,若利用分布B(n,0.157 35),应注意的是,所求概率值乘以2并不等于用式(1)求得的结果,这一点要特别注意。

[ 1 ]张公绪. 新编质量管理学[M]. 北京:高等教育出版社, 2003.

[ 2 ]张公绪. 选控图理论与实践[M]. 北京:人民邮电出版社, 1984.

[ 3 ]宋明顺. 质量管理学[M]. 北京:科学出版社, 2005.

[ 4 ]孙静,张公绪. 常规控制图标准及其应用[M]. 北京:中国标准出版社, 2000.

[ 5 ]国家质量技术监督局. GB/T 4091—2001. 常规控制图[S]. 北京:中国标准出版社, 2001.

[ 6 ]王昕,程希明. 概率论与数理统计案例教学方法探析[J]. 沈阳师范大学学报:自然科学版, 2013,31(3):372-375.

[ 7 ]郭彦兰,崔利荣,张晨宇. 统计控制图的异常判断准则分析[J]. 数理统计与管理, 2007,26(3):468-474.

[ 8 ]余忠华,吴昭同. 控制图模式及其智能识别方法[J]. 浙江大学学报:工学版, 2001,35(5):521-525.

[ 9 ]温德成,安玉红. 均值变化下的控制图3σ控制界限的经济性分析[J]. 统计与决策, 2008(21):151-152.

[10]励晶晶,郭文. 两类错误下的样本容量选择[J]. 统计与决策, 2010(15):14-18.

[11]王兆军. 关于动态质量控制图的设计理论[J]. 应用概率统计, 2002,18(3):316-333.

[12]王金玉,章红雨,刘军,等. 一种多指标质量动态控制图及其应用[J]. 数理统计与管理, 2007,26(1):101-105.

[13]昝涛,费仁元,王民. 基于神经网络的控制图异常模式识别研究[J]. 北京工业大学学报, 2006,32(8):673-676.

[14]刘建斌,张维铭. 可变抽样区间的非参数控制图[J]. 数理统计与管理, 2002,21(4):22-27.

[15]刘建斌,张维铭. 可变抽样区间的非参数控制图[J]. 数理统计与管理, 2002,21(4):22-27.

[16]张庆华,张丽莉,程国全,等. 控制图及过程能力分析在供应商质量管理中的应用研究[J]. 物流技术, 2010,29(1):102-105.

[17]王彩玲,师义民. 基于批均值的自相关过程EWMA控制图[J]. 沈阳师范大学学报:自然科学版, 2010,28(3):387-390.

[18]张敏,何桢. 自相关过程的质量控制图[J]. 数理统计与管理, 2007,26(1):96-100.

Designofalarmrulesbasedonplottingdistributionawayfromcenterline

WENXueying,SUNWei

(Applied Technology College, Dalian Ocean University, Dalian 116300, China)

The article introduces basic concepts about stability and abnormality in the production process, points out the essential differences between them depend on whether certain distribution abided by quality characteristics will change, by showing on the control charts if sample plotting can arise in the form of random distribution. When quality feature obeys normal distribution, sample plotting which tends to distribute randomly approaching to the center line presents stability; otherwise abnormality. One form of the abnormality is sample dotting beyond the control limit, which can be solved by Shewhart’s distinguished alarm rule that a point out of limit means abnormality. The other form is that in spite of sample dotting within the control limit, there exist the following dotting irrandom distributrion phenomena in the control domain such as monotone arrangement ,adjacent points altermating up and down movements among many continuous sample points, sample points fluctuating greatly relative to the centre line. In view of the judging abnormality from irrandom process shown sample dotting, the corresponding alarm rules should be taken advantage of. Therefore, such sample plotting that fluctuates greatly relative to the center line should be selected and the design of alarm rules in the production can be obtained simultaneously.

quality management; control charts; alarm rules; design

2014-03-23。

辽宁省教育厅高等学校科学研究项目(20060842); 辽宁省高等教育教学改革研究项目(辽教发[2009]141号)。

闻学颖(1974-),女,辽宁大连人,大连海洋大学助理研究员。

1673-5862(2014)04-0537-04

O175

: A

10.3969/ j.issn.1673-5862.2014.04.017