一类TS模糊有记忆系统的保性能控制器设计

王 艳 华

(朝阳师范高等专科学校 数学计算机系, 辽宁 朝阳 122000)

王 艳 华

(朝阳师范高等专科学校 数学计算机系, 辽宁 朝阳 122000)

在控制系统中,不仅要求系统能够保持稳定,还要求系统能够满足一定的性能指标,由于T-S模型可以有效的描述许多非线性系统,所以采用带有状态不确定项的T-S模糊系统对控制系统进行描述,又由于被控量的时滞现象大量存在于系统中,所以通过设计有记忆模糊状态反馈控制器,实现系统的保性能控制,同时找到保性能函数的一个上界。首先,通过构造李雅普诺夫(Lyapunov)二次函数,根据李雅普诺夫(Lyapunov)稳定性理论,证明在此有记忆模糊状态反馈控制器下,对于T-S模糊系统中含有的所有不确定项,形成的闭环系统是渐近稳定的,同时找到保性能函数的一个上界;其次,通过利用线性矩阵不等式(LMI)技术,应用Matlab中的LMI工具箱求解出有记忆状态反馈控制器的反馈增益矩阵;最后,通过仿真算例说明方法的有效性。

有记忆; T-S模糊系统; 线性矩阵不等式(LMI); 保性能

0 引 言

实际工程中,由于被控量的时滞现象大量存在于系统中,所以采用有记忆控制能更好地实现系统的性能。而自1972年,Chang等[1]首次提出了保性能控制,就受到了很多学者的关注,并在此领域进行了大量的研究与探索[2-6],文献[2]对具有变时滞的参数不确定中立系统进行保性能控制的研究;文献[3]研究了带有多输入输出时滞的范数有界不确定离散系统的稳定性,并利用凸优化技术给出了一个可保成本的有效迭代算法;文献[4]针对广义马尔科夫跳变时滞系统,考虑了保成本控制问题;文献[5]针对一类存在时滞的不确定切换模糊系统,利用平行分布补偿算法,给出保性能控制器的设计方法;文献[6]研究了一类带有非线性参数扰动的中立型时滞系统的保成本控制问题;文献[7]研究了中立时滞系统的有记忆状态反馈保成本控制器;文献[8]研究了T-S模糊有记忆非易碎系统保成本控制器设计问题;文献[9]研究了不确定时滞连续广义线性系统在有记忆状态反馈作用下的鲁棒H∞控制问题;文献[12] 研究一类不确定离散关联系统的鲁棒分散H∞控制问题,并满足H∞性能指标;文献[13]对T-S模糊系统设计了一种H∞控制器,从而实现非线性系统的二次稳定;文献[14]对闭环T-S模型系统,给出了一种新的稳定性分析和系统化设计方法,但它的T-S模型只是一种标称模糊系统,并不含有参数不确定项和外部扰动,因此减弱了系统鲁棒性。目前,对于有记忆不确定T-S模糊系统的保性能控制进行研究的较少,因此本文将研究含有状态不确定项T-S模型的有记忆保性能控制问题。

1 预备知识及问题描述

1.1相关引理

引理1[9]对于任意具有相应维数的实矩阵X和Y,则对于任意正数α0,下列不等式成立

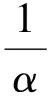
引理2[5]对任意满足FT(t)F(t)≤I的F(t)∈Rp×q,有

2xTDF(t)Ey≤εxTDDTx+ε-1yTETEy

对任意向量x∈Rp,y∈Rq和常数ε0成立,其中D,E是适当维数的常数矩阵。

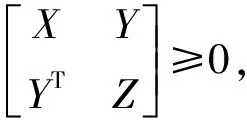
1.2问题描述

现考虑一类含有状态不确定项的T-S模糊模型[15],

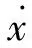
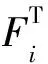
考虑如下形式有记忆状态反馈模糊控制器,

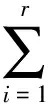
其中,K1i,K2i∈Rm×n是第i个规则的反馈控制器增益。

将有记忆状态反馈控制器式(2)带入系统式(1)中,得到闭环系统为

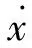
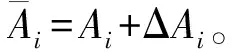
对于闭环系统(3),定义保性能函数的二次性能指标如下:

本文的目的就是设计有记忆状态反馈模糊控制器(2),对于系统中含有的所有不确定项,不仅能使得闭环系统(3)是渐近稳定,而且能满足保性能函数的二次性能指标。

2 主要结果

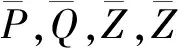
证明 构造Lyapunov函数为

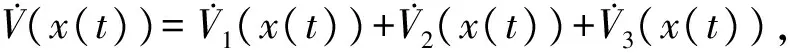
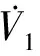
根据引理3,得到,

由式(2)和式(3)得,

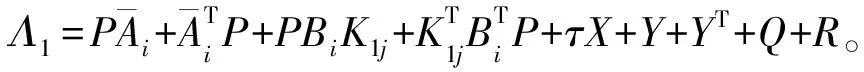
由不确定项满足ΔAi=DiFi(t)Ei,根据引理1,引理2和schur补引理[10],式(8)满足

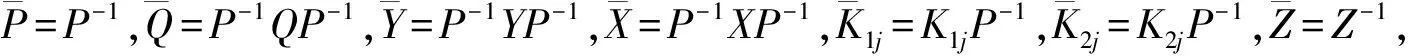
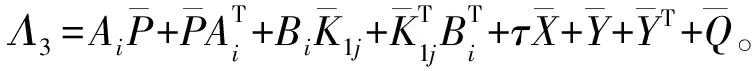
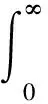
所以保成本函数性能指标的一个上界值为

3 数值算例

考虑全局模糊系统(3)由两条规则描述,其中

利用Matlab中的LMI工具箱,可得

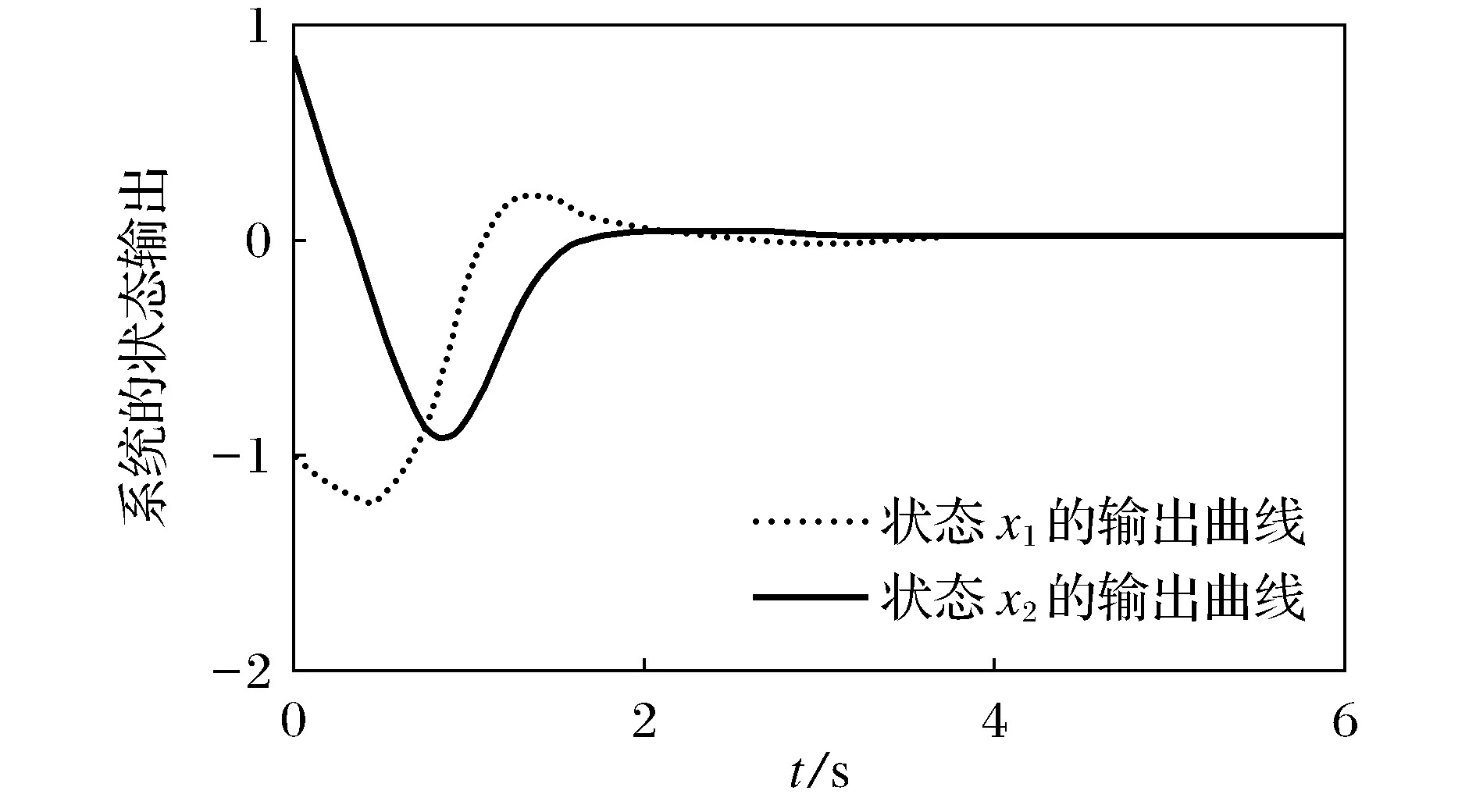
图1 状态随时间的输出曲线

假设系统的初始条件为:x(0)=[-1 1]T,F1(t)=F2(t)=sin(πt)I2,I2为二维单位矩阵,取隶属度函数为μ2(t)=1-μ1(t),μ1(t)=1/(1+exp(-2x1))。

由Matlab得到系统的状态输出曲线如图1所示。

4 结 论

本文主要基于含有状态不确定项的T-S模糊系统,通过设计有记忆反馈模糊控制器,实现系统的保性能控制,首先,通过构造Lyapunov函数,根据Lyapunov稳定性理论,证明在此有记忆反馈控制器下,对所有的不确定项,形成的闭环系统是鲁棒渐近稳定的,同时找到保成本函数的一个上界,其次,通过利用线性矩阵不等式(LMI)技术,应用Matlab中的LMI工具箱求解控制器的反馈增益矩阵,最后,数值算例说明了方法的有效性,仿真结果也表明系统是渐近稳定的。

[ 1 ]CHAND S, PENG T. Adaptive guaranteed cost control of systems with uncertain parameters[J]. IEEE Automa Contr, 1972,17(4):474-483.

[ 2 ]YU K W, LIEN C H. Delay-dependent conditions for guaranteed cost observer-based control of uncertain neutral systems with time-varying delays[J]. Ima J Math Control I, 2007,24(2):383-394.

[ 3 ]李阳. 多时滞不确定离散系统稳定性的凸优化算法[J]. 科学技术与工程, 2013,20(13):5825-5828.

[ 4 ]张鹏,曹江涛,王国良. 一种广义马尔科夫跳变时滞系统的保成本控制[J]. 生物数学学报, 2013,28(1):153-158.

[ 5 ]刘毅,孙丽颖. 一类不确定切换模糊时滞系统的保性能控制[J]. 控制工程, 2013,20(3):521-525.

[ 6 ]张勇,唐功友,赵友刚. 一类大时滞非线性网络控制系统的H∞保成本控制[J]. 控制理论与应用, 2009,26(7):800-804.

[ 7 ]CHEN B, LAM J, XU S. Memory state feedback guaranteed cost control for neutral delay systems[J]. Int J Innov Comput I, 2006,2(2):293-303.

[ 8 ]杭阿芳,陈丽换. T-S模糊有记忆非易碎系统保成本控制器设计的LMI方法[J]. 西南大学学报:自然科学版, 2012,34(11):125-131.

[ 9 ]谭冲,张睿智,张显. 不确定时滞广义线性系统的有记忆状态反馈鲁棒H∞控制[J]. 黑龙江大学自然科学学报, 2009,26(4):458-464.

[10]俞立. 鲁棒控制----线性矩阵不等式处理方法[M]. 北京:清华大学出版社, 2002:6-9.

[11]晁宁,李言俊. 基于分段连续推力的晕轨道控制方法[J]. 宇航学报, 2011,32(9):1925-1931.

[12]张晓妮, 徐兆棣. 具有控制器增益变化的不确定离散关联系统的鲁棒分散H∞控制[J]. 沈阳师范大学学报:自然科学版, 2006,24(1):6-9.

[13]LIU Xiaodong, ZHANG Qingling. Approaches to quadratic stability conditions andH∞control designs for T-S fuzzy systems[J]. IEEE T Fuzzy Syst, 2003,11(6):830-839.

[14]XIU Zhihong, REN Guang. Stability analysis and systematic design of Takagi-Sugeno fuzzy control systems[J]. Fuzzy Set Syst, 2005,151(1):119-138.

[15]TAKAGI T, SUGENO M. Fuzzy identification of systems and its applications to modeling and control[J]. IEEE T Syst Man Cy B, 1985,15(1):116-132.

GuaranteedcostcontrollerdesignforaclassofT-Sfuzzymemorysystem

WANGYanhua

(Mathematics and Computer Department, Chaoyang Teachers College, Chaoyang 122000, China)

In control systems, the systems are not only required to remain stable but should satisfy certain performance indies. As the T-S model could describe many nonlinear systems effectively, the T-S model with the state uncertainty can describe the control systems. Many delay phenomena of the controller exist in the systems so the memory fuzzy feedback controller is designed to achieve guaranteed cost control of the system and obtain an upper-bound for the given guaranteed cost control. Firstly, by constructing a Lyapunov function and based on the Lyapunov stability theory, it is proved that the closed-loop system is asymptotically stable for all uncertainty in the systems through the application of this memory fuzzy feedback controller and an upper-bound for the given guaranteed cost control is acquired. Secondly, by using the linear matrix inequality (LMI) technique in MATLAB, the feedback controller gain would be found out. Finally, the simulation example is given to illustrate the validity of the proposed method.

memory; T-S fuzzy system; linear matrix inequality (LMI); guaranteed cost

2014-05-04。

国家自然科学基金资助项目(61070242)。

王艳华(1980-),女,辽宁朝阳人,朝阳师范高等专科学校讲师,硕士。

1673-5862(2014)04-0486-05

O231.2

: A

10.3969/ j.issn.1673-5862.2014.04.007