某型航空发动机前支承动刚度的有限元分析

丁哲民

(长沙航空职业技术学院，湖南 长沙 410124)

影响发动机振动特性的主要因素包括航空发动机静子支承动刚度，精准的静子系统动力特性是研究转子系统动力特性中临界转速、振型、不平衡响应以及传递特性的前提。现有文献表明，转子和机匣间的动力耦合关系是用支承动刚度表征的。支承动刚度是频率的函数，与转子的临界转速密切相关，体现了在研究机匣支撑系统的频率范围内，位移响应和激振力的关系。所以在设计发动机时，获得动刚度随频率的变化曲线是分析支承动刚度的重要条件。

目前航空发动机支承结构的刚度系数的范围都是靠经验给出的，数据的准确性对转子特性计算至关重要。现阶段获得航空发动机支承结构刚度系数的主要手段分试验和数值模拟计算两种方法。但是通过试验方法获得结果受很多因素制约。(例如:试验仪器精度差;费时费力费钱)。随着计算力学的发展和大型分析软件的开发，在结构动力学分析领域中，经常使用有限元进行计算，所以静子系统的动力特性用计算的方法求出是很有必要的。

1 发动机前支撑的动力模型

使用有限元的计算方法，计算模型航空发动机前支承动刚度，建立某型航空发动机前支承结构的三维实体模型，为后续计算做准备，这些原始数据不仅直接影响到网格的划分，而且还会影响计算结果。由于某型航空发动机前支承具有复杂的结构，建立三维实体模型要适当的简化其中的结构。在保证充分反映力学特性和结构特性的前提下，对所关心的某型航空发动机前支承结构模型关键地方精细化，对不关键的区域，在不影响关键地方结构特性的情况下进行最大程度简化。某型航空发动机前支承结构主要为压气机静子，由前机匣、后机匣、进气机匣、第二、三、四、五级整流器组成。针对前支承动刚度的计算要求，根据实际结构尺寸，利用UG三维建模软件建立准确的实物模型。图1是模型航空发动机前支承实体模型内部结构。图2是某型航空发动机前支承结构三维实体模型。

图1 某型航空发动机前支承实体模型内部结构

图2 某型航空发动机静子支承结构三维实体模型

2 计算力学模型

2.1 建立有限元模型

有限元的基本思想:将表示结构的连续体离散为若干个子域，单元之间通过其边界上的节点连接成组合体。将某型航空发动机前支承结构的三维实体UG模型导入ANSYS软件，选择合理的单元类型，确定合适的单元尺寸，建立某型航空发动机前支承结构的有限元模型。某型航空发动机前支承结构是由不用结构、不用形状、不同厚度的压气机机匣、静子叶片等部件构成，结构非常复杂。通过认知分析，选择子域类型为SOLID95。SOLID95是3维8节点实体子域，子域定义20个节点，具有应力刚度、蠕变、大变形、大应变和蠕变能力。它可以保证不规则的形状的精确度损失较小，具有协调的位移性质函数，对模型的曲线边界的拟合能力强。通过多次试验和分析，将用有限元的方法划分模型航空发动机前支承结构，其网格单元尺寸设置为22mm左右，在保证计算精度的同时，确保了有限元计算规模不会太大。考虑到模型结构较为复杂，采用自动网格划分，合理设置划分精度，控制网格大小疏密，有效的确保了最终的有限元模型的合理性。共划分得到913888个子域，325542个节点。图3是模型航空发动机前支承结构有限元模型。

图3 某型航空发动机前支承结构有限元模型

2.2 有限元分析理论

有限元法的分析过程是先分后合。即先进行单元分析，在建立了单元刚度方程以后，再进行整体分析，把这些方程集成起来，形成求解区域的刚度方程，称为有限元位移法基本方程。

采用虚位移原理建立的整体刚度方程就是整体结构上所有节点载荷所做的虚功等于所有单元的虚应变能之和，即

式中 δd= ［δd1δd2… δdN］T为整体节点位移虚位移向量。将虚应变与节点位移之间的关系代入，可得

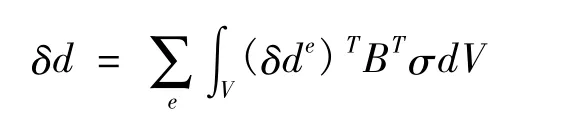
将单元节点位移向量de转化为整体节点位移向量d，即引入变换矩阵Ae，有

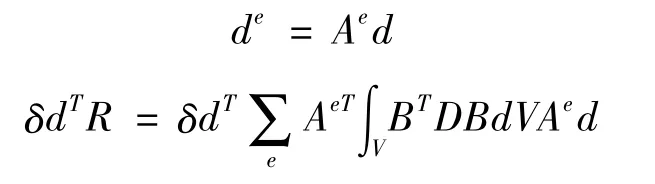
考虑到虚位移的任意性，等式两边与δd相乘的矩阵应该相等，得到整体平衡方程

Kd=R

3 有限元计算

3.1 有限元计算物理模型

按照某型航空发动机在机体上的实际安装情况确定计算模型的边界条件，对所建立的某型航空发动机前支承结构有限元模型进行模态分析。某型航空发动机通过主安装节和辅助安装节固定在飞机上，主安装节三个支承位于靠近发动机重心的第六级压气机机匣上。燃烧室外套的后安装边上方两侧是辅助安装节。对安装节加以约束。图4是模型航空发动机前支承结构有限元模型。在给出的边界条件下，对该模型进行模态计算，计算频率范围为0—2000Hz。由计算得到前八阶模态图。图5为某型航空发动机前支承结构前八阶模态频率。

图4 某型航空发动机前支承结构有限元模型约束图

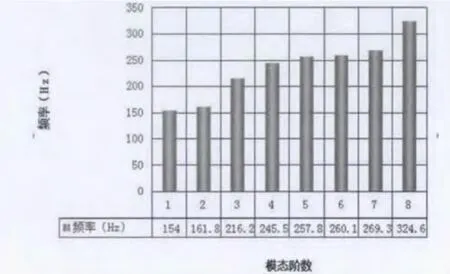
图5 某型航空发动机前支承结构前八阶模态频率

3.2 有限元计算结果

因为结构本身参数决定动刚度的理论值，作用力的大小对动刚度的理论值没有影响。对压气机静子机匣前支承施加水平方向、垂直方向的激振力，分析机匣前支承垂直方向、水平方向的谐响应。所以，在研究模型航空发动机静子支承系统前支承结构谐响应时，在某型航空发动机静子支承系统前支承处加1000N的简谐激振力，求解在每一个自由度上的谐位移。计算频率范围为0～300Hz。为确保计算结果的准确性和可比性，分别在静子支承系统前支承处选取4个不同节点，分别对其进行谐响应分析，将计算前支承的4个节点沿水平方向和沿垂直方向的频率响应曲线分别绘在一幅图上，如图6和图7所示。

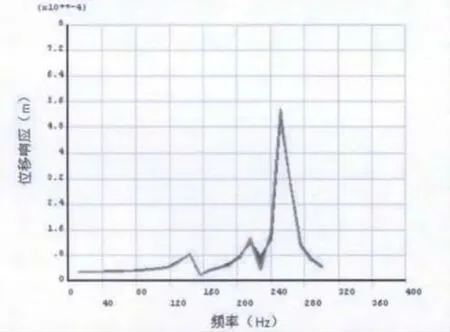
图6 某型航空发动机前支承沿水平方向频率响应曲线

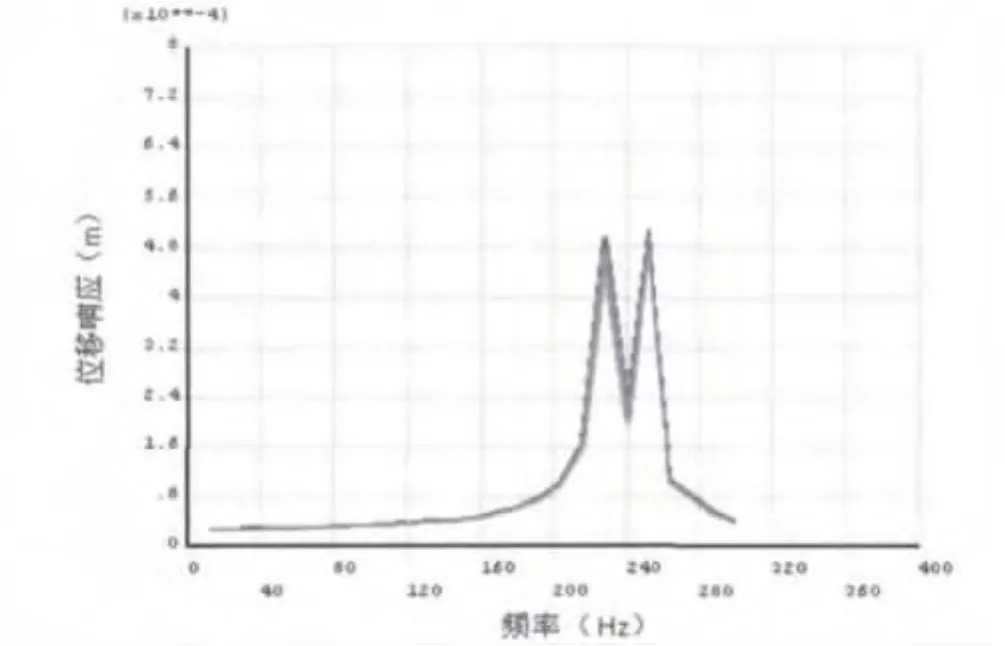
图7 某型航空发动机前支承沿垂直方向频率响应曲线

由图6前支承沿水平向频率响应曲线和图7前支承沿垂直向频率响应可以看出:

(1)所计算发动机静子支承系统前支承4个节点沿水平方向动刚度随频率变化曲线基本上重合，计算前支承4个节点沿垂直方向刚度随频率变化应曲线也基本重合。

(2)激振频率在0－300Hz时，在水平方向随着频率变化，静子支承系统前支承的动刚度值有三处突降，这三处分别是 144Hz、216Hz、252Hz处，这几个频率正是频率响应曲线在水平方向上出现共振峰的位置，上面频率所对应的刚度极小值分别为1.2109× N/m、0.7889 ×N/m、0.1912 ×N/m;而在垂直方向随着频率变化，静子支承系统前支承的动刚度值在228Hz和252Hz两处出现刚度突降，这两个频率是频率响应曲线在垂直方向上出现共振峰的位置，对应的刚度极小值为0.2193×N/m、0.2082×N/m。

图8 前支承沿水平方向刚度随频率变化对比图

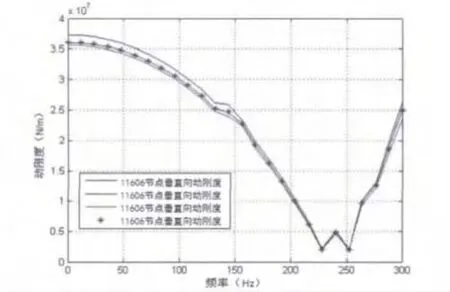
图9 前支承沿垂直方向刚度随频率变化对比图

对某型航空发动机前支承动刚度计算结果进行了简单验证，通过对有理论解的简单梁进行建模、模态分析、谐响应分析、动刚度计算，验证计算方法及参数设置的的正确性。并且将所得到的某型航空发动机前支承的谐响应分析结果与模态分析结果进行对比。前支承沿水平方向、垂直方向刚度随频率变化对比图分别如图8、图9所示。通过对比发现二者吻合良好。在一定程度上验证了计算结果的合理性。

4 结论

(1)对于航空发动机静子系统这样复杂的结构进行有限元分析，需要对结构进行简化。本文采用的对压气机叶片、前机匣、压气机后机匣等部件分别进行简化，然后整体建立有限元模型的简化方法是可行的。

(2)与8节点的实体单元相比，在计算静子系统动力特性时20节点实体单元建模具有更高的精度。基于20节点的实体单元可以更好的适应不规则的形状，同时又不会损失太多的精确度，应用其进行静子系统动力特性计算时，得到的结果更为精确。

(3)某型航空发动机前支承沿水平方向的动刚度曲线在0Hz处为3.662×107N/m，随着频率的增大而减小，在144Hz处为1.267×107N/m，在156Hz处增大到5.867×107N/m，之后又随频率的增大而下减小，在216Hz处为0.817×107N/m;沿垂直方向的动刚度曲线在 0Hz处为 3.626×107N/m，随着频率的增大而减小，在216Hz处为0.286 ×107N/m。

［1］张大义，母国新，洪杰.航空发动机转子支承系统刚度计算中的几个问题［J］.战术导弹技术，2005，(2).

［2］周明，倪纬斗，于文虎，等.某单轴式燃气轮机支承刚度计算分析［J］.山东电力技术，1998，(2).

［3］饶寿期.有限元法和边界元法基础［M］.北京:北京航空航天大学出版社，1990.

［4］刘长福，邓明.航空发动机结构分析［M］.西安:西北工业大学出版社，2006.

［5］杜平安，甘娥忠，于亚婷.有限元法——原理、建模及应用［M］.北京:国防工业出版社，2006.