基于贝叶斯和模糊L-M网络的变压器故障诊断

黄新波，宋桐，王娅娜，李文君子，林淑凡

(西安工程大学电子信息学院，西安市710048)

0 引言

智能化变电站的安全可靠运行是实现整个智能电网稳定运行的主要条件之一，而智能化电力变压器又是智能化变电站的重要组成部分，因此及时、可靠地对智能化电力变压器潜在的故障进行诊断，对于保障智能电网运行具有十分重要的意义［1］。如何准确预测变压器的运行状态，已成为电力行业研究的重点。目前油中溶解气体分析法 (dissolved gas analysis，DGA)作为变压器油中溶解气体监测技术中最为成熟的技术之一，已被列为油浸式变压器32项预试项目中的第1位，对诊断变压器故障状况具有显著效果［2］。然而，电力系统中的重要设备电力变压器结构复杂，故障不确定因素很多，正确诊断很难，因此我国目前诊断变压器故障最方便有效的方法——DGA三比值法(IEC和国标推荐)在现场应用中也发现有“缺编码”、编码边界过于绝对等不足［3］，故各种智能技术如模糊推理、人工神经网络等已被用于变压器故障诊断以提高诊断准确率［4］。

在宁夏银川东±660kV换流站项目中，通过对在线监测技术的研发工作，实现了变压器、断路器、容性设备和氧化锌避雷器等一次设备的在线监测。其中针对变压器采用了油色谱、局部放电、铁芯接地、变压器油温等监测方案，上述装置已经获得了准确的运行数据，但如何根据监测数据诊断变压器运行状态成为一个关键技术问题。本文采用贝叶斯方法来确定超参数，使其在网络的训练过程中自适应地调节超参数的大小，并使其达到最优，从而提高神经网络的泛化能力。同时，结合模糊理论法简化L-M(Levenberg-Marquardt)神经网络的输入单元数，贝叶斯正则化算法提高网络的泛化能力，建立贝叶斯正则化的模糊L-M神经网络预测模型。最后，与几种常用的预测方法进行对比研究，以验证本文建立的模型的仿真和预测能力。

1 贝叶斯正则化原理

神经网络的推广能力是衡量神经网络结构性能好坏的一个重要标志，“过度训练”的神经网络会对训练样本集达到较高的匹配效果，但是对于一个新的输入样本矢量可能会产生与目标矢量差别较大的输出，因而神经网络不具有或具有较差的推广能力［5］。我们采用贝叶斯正则化的神经网络算法。一般算法是以均方误差函数为目标函数，因而权值问题不能得到优化，但贝叶斯正则化方法则在目标函数中增加权值这一项，并能自动调节参数，优化网络结构，从而提高网络的泛化与推广能力［6］。

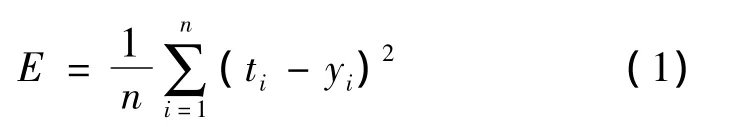
式中:n为样本总数;ti为网络的期望输出值;yi为实际输出值。

但贝叶斯正则化方法为了提高网络的泛化能力，在目标函数里加上网络权值平方的算术平均值，即目标函数变换为:

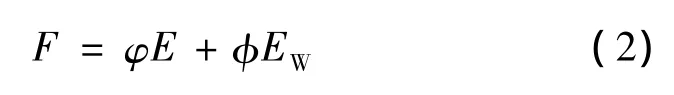
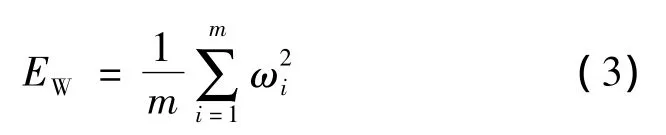
式中:ωi为神经网络的连接权值;m为神经网络连接权的个数;φ、φ为目标函数的参数。贝叶斯正则化方法可以在网络训练过程中自适应的调节参数φ、φ的大小。在保证网络误差平方和最小的前提下，能够有效地控制网络的复杂度，进而有助于显著提高网络的泛化能力。

φ、φ控制着其他参数(权及阈值)的分布形式，被称为超参数。超参数的大小决定着神经网络的训练结果。若φ＜＜φ，则训练算法的目的在于尽量减小网络的训练误差;若φ＞＞φ，则训练算法的目的在于使网络产生更为平滑的响应，即尽可能减少有效的网络参数，以弥补较大的网络误差。在实际应用中，这二者之间需要折中考虑，即极小化目标函数在减少网络训练误差的同时，还能降低网络结构的复杂性。常规的正则化方法通常很难确定正则化参数的大小，而采用贝叶斯理论可以在网络训练过程中自适应地调节正则化参数的大小，并使其达到最优。

2 变压器故障诊断模型系统架构

在变压器故障诊断中，基于贝叶斯正则化的模糊L-M网络模型的建立主要分为3个部分:数据预处理，诊断模型的建立以及应用与评估。具体变压器故障诊断模型总体架构如图1所示。

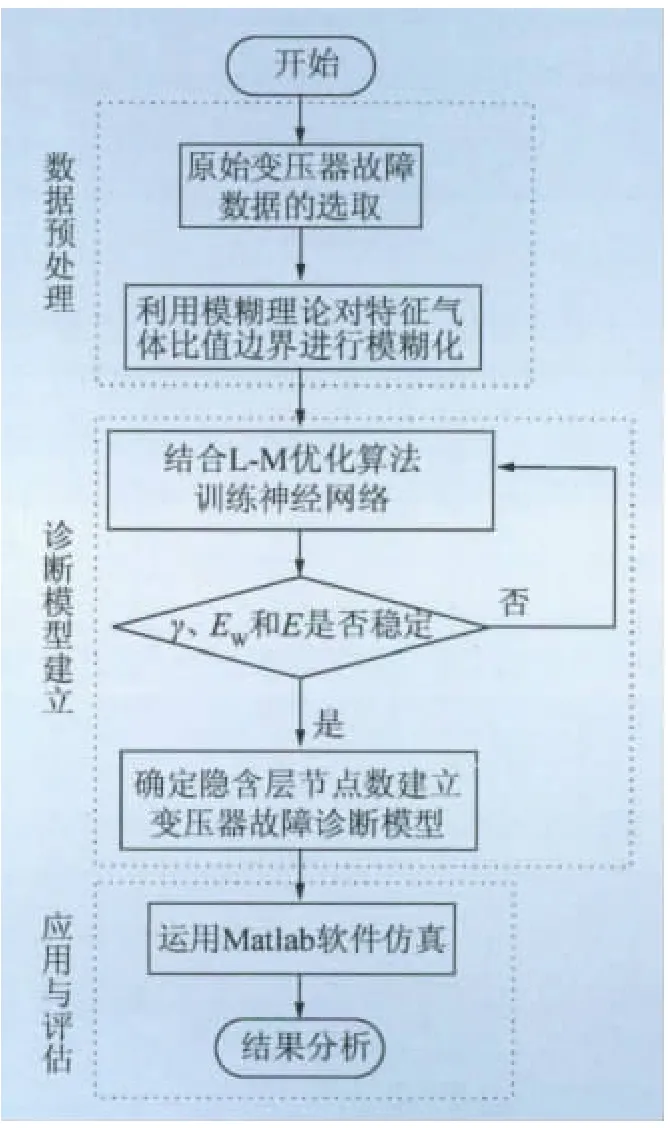
图1 基于贝叶斯正则化模糊L-M网络的变压器故障诊断框图Fig.1 Transformer fault diagnosis based on Bayesian regularization and fuzzy L-M networks

由图1可知，首先，运用模糊理论对数据进行预处理作为神经网络的输入;其次，基于贝叶斯正则化方法对L-M神经网络进行优化，以F=φE+φEW作为目标函数进行训练，当γ、EW、E稳定时，变压器故障诊断模型建立;最后，对所建立的模型代入训练和测试数据进行仿真，根据运行结果对网络进行评估。

2.1 模型输入的模糊化处理

模糊三比值法是引入模糊数学理论来诊断变压器故障，将三比值法的比值边界区间模糊化，建立基于三比值法的模糊隶属函数。根据传统三比值法编码规则，特征气体的体积(单位为 μL/L)之比:V(CH4)/V(H2)，V(C2H4)/V(C2H6)，V(C2H2)/V(C2H4)的比值的划分边界分别为“0.1”，“1”，“3”。根据经验知识，将“0.1”的边界模糊为“0.08～0.12”，“1”的边界模糊为“0.85～1.15”和“0.9～1.1”，“3”的边界模糊为“2.9～3.1”和“2.85～3.15”［7］。运用指派法将各气体比值分别隶属于0、1、2的隶属度函数指派为偏小型Γ、中间型岭型、偏大型Γ模糊分布。所以，当C2H2与C2H4的比值编码为0、1、2 时，相应隶属函数为 u0(xbi)、u1(xbi)、u2(xbi)，然后根据最大隶属度原则确定最终编码。特征气体V(CH4)/V(H2)，V(C2H4)/V(C2H6)的比值编码确定方法同V(C2H2)/V(C2H4)比值编码方法一致。模糊三比值法的优点是在一定程度上克服了编码边界区间过于绝对化的缺点，有利于提高诊断准确率［7］。因而，本文所用到的特征气体样本数据变换为由“0、1、2”组成的编码序列作为网络的输入。

2.2 L-M网络训练原理

神经网络建模的实质是找出蕴含在有限样本数据中的输入和输出之间的本质联系，即映射关系，从而对未经训练的输入也能给出合适的输出，即具备泛化功能。参阅文献［8-10］可知，标准BP算法采用的是最速梯度下降法修正权值，训练过程从某一起点沿误差函数的曲面逐渐到达最小点使误差为0。当网络复杂时，在训练的过程中可能会陷入某个局部最小点，并且收敛速度缓慢。为了克服算法中的这些不足，本文采用L-M优化算法，又称为阻尼最小二乘法。它比传统的BP及其他改进算法迭代次数少，收敛速度快，准确度高。

其权值调整公式如下:

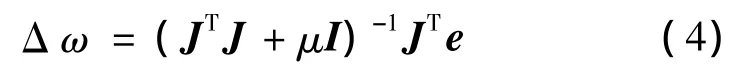
式中:e为误差向量;J为误差对权值微分的雅可比矩阵;μ为标量，当μ增加时，它接近于具有较小学习速率的最速下降法，当μ下降到0时，该算法就变成高斯 －牛顿法了。因此，L-M算法是在最速梯度下降法和高斯 －牛顿法之间的平滑过度［11］。

L-M算法具体的迭代步骤如下:

(1)将所有输入送到网络并计算出网络的输出，另用误差函数计算出训练集中所有目标的误差平方和;

(2)计算出误差对权值微分的雅可比矩阵J;

(3)用公式(4)求出Δω;

(4)用ωi+Δω重复计算误差的平方和，其中ωi(i=1，2，…，n)为网络权值。如果新的和小于步骤(1)中计算的和，则用μ除以θ(θ＞1)，并有ωi=ωi－1+ Δω，转到步骤(1);否则，用 μ 乘以 θ，转到步骤(3)。当误差平方和减小到某一目标误差时，算法即被认为收敛［12］。

2.3 贝叶斯正则化参数的确立

变压器故障诊断模型建立的重点在参数φ和φ的确立，即如何确立φ，φ的大小使参数γ、EW、E的大小趋于稳定，进而保证网络训练达到最优。下面通过贝叶斯公式推出变量φ，φ的取值。

φ和φ的后验分布根据贝叶斯定理则有:

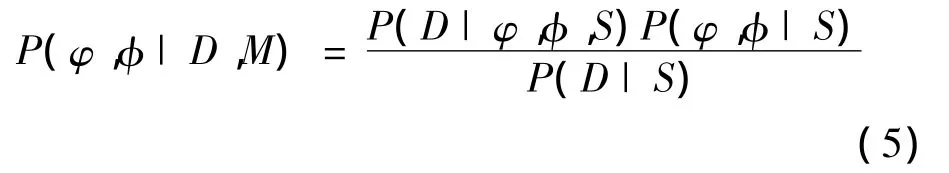
假设先验分布P(φ，φ|S)是一种很宽的分布函数，且φ，φ这2个变量的后验概率与式(5)中归一化因子P(D|S)无关，因此，只需使似然函数P(D|φ，φ，S)最大，即可使φ，φ的后验分布最大。

贝叶斯方法着眼于权值在整个权空间中的概率分布。若用S表示网络结构，在网络结构已确定的情况下，在没有样本数据时，若知道权值的先验分布P(ω|φ，S)，其中:ω为权值向量，有了样本数据集D后，权值的后验分布为P(ω|D，φ，φ，S)，根据贝叶斯定理有:

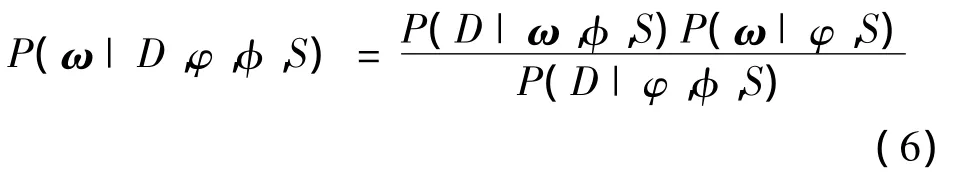
式中:P(D|φ，φ，S)为全概率;P(ω|φ，S)表示权值向量的先验概率密度函数;P(D|φ，φ，S)表示权值给定时输出的似然函数。在没有数据时，由于对权的分布只是很少的知识，因此先验分布是一个很宽的分布;一旦有了数据，它就可转化为后验分布，后验分布较为紧凑，即只有在很小范围中的权值才可能与网络的映射一致。由公式(6)可知，为得到后验分布P(ω|D，φ，φ，S)，必须知道 P(ω|φ，S)和P(D|ω，φ，S)，下面即为二者的具体求解过程。

(1)ω的先验分布P(ω|φ，S)的求解;在没有权值的先验知识时，假设P(ω|φ，S)服从高斯分布，则有:

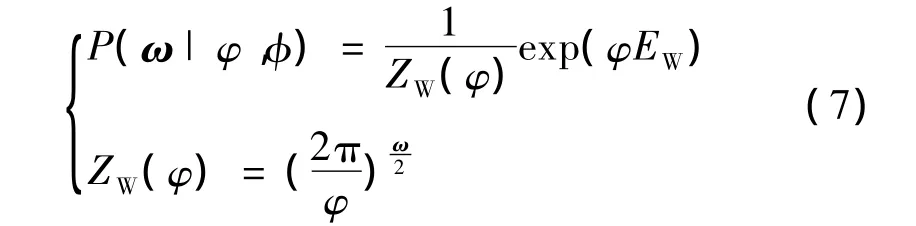
(2)似然函数P(D|ω，φ，S)的求解如下:

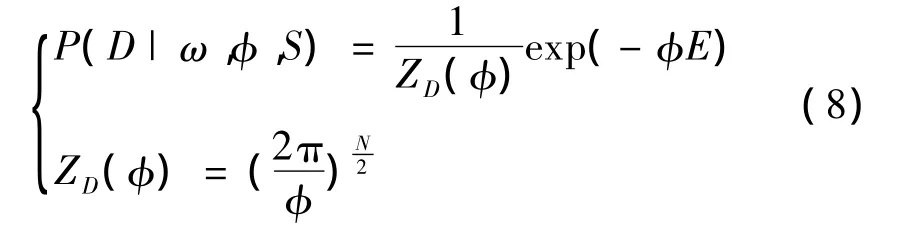
(3)权值后验分布 P(ω|D，φ，φ，S)的求解。注意到P(D|φ，φ，S)与ω无关，因此代入P(ω|φ，S)和P(D|ω，φ，S)可以得出权值的后验分布为

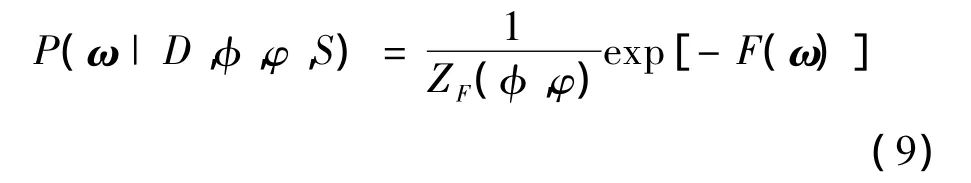
由于ZF(φ，φ)与ω无关，因此最小化F(ω)可以求得后验分布的最大值，此时所对应的权值即为所求。若φ＜＜φ，网络训练将使得误差尽可能小;若φ＞＞φ网络训练将尽可能减小有效地网络参数，可以弥补较大的网络误差。可见采用新的目标函数，在保证网络训练误差尽可能小的情况下，使得网络的参数尽可能小，从而自动缩小了网络的规模。

由公式(6)和(9)可得:

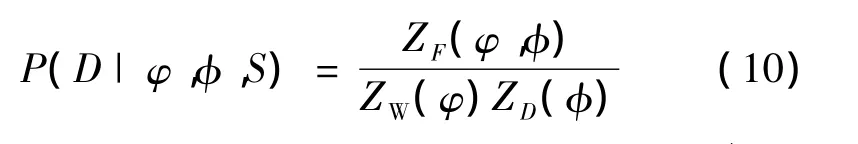
为了确定 ZF(φ，φ)，把 F(ω)在最小点 ω*展开，由于梯度为0，因此近似有:

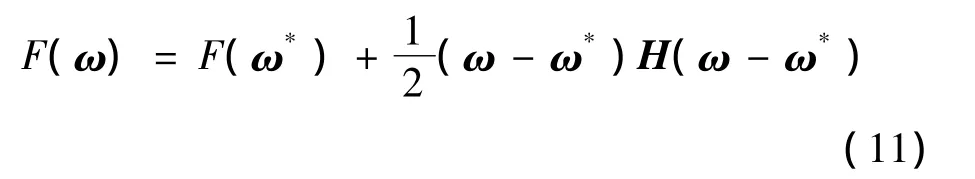
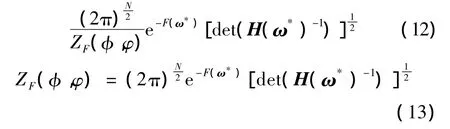
将式(13)代入式(10)，两边取对数，并利用最优值的一阶条件可以获得最优的正则化参数:

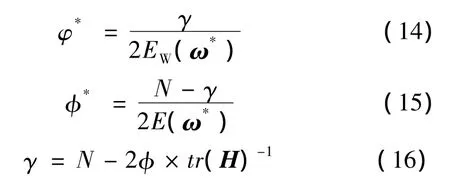
式中:N为网络权值的总个数;γ为N个总参数中真正起作用的有效参数的个数，γ∈(0，N)，它反应了网络的实际规模。通过参数φ和φ的确立，可使L-M算法训练神经网络时运用含有权值的误差目标函数，保证了网络误差平方和最小的前提下，能够有效地控制网络的复杂度，进而有助于显著提高网络的泛化能力［13］。

3 实例分析

3.1 研究样本的来源

本文进行仿真试验的数据来源于宁夏银川东±660kV换流站的主变压器油色谱监测智能电子设备(intelligent electronic device，IED)，此IED 就地安装于主变智能组件柜，通过IEC61850通信规约实现了变压器油中溶解气体的监测与数据远传等功能。宁夏银川东±660kV监控中心通过安装后台软件界面，实时监测变压器各特征气体浓度。主变压器油色谱监测IED的现场安装，如图2所示;图3为根据智能变电站监控中心后台软件界面得到的现场油色谱实时数据图。

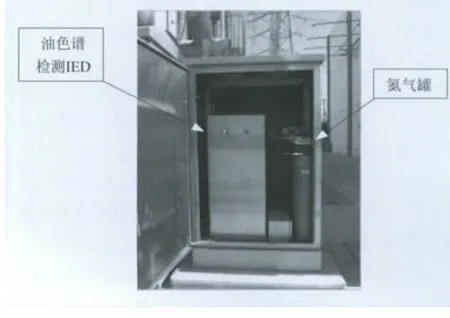
图2 油色谱监测IED现场安装图Fig.2 Installation pictures of DGA monitoring IED

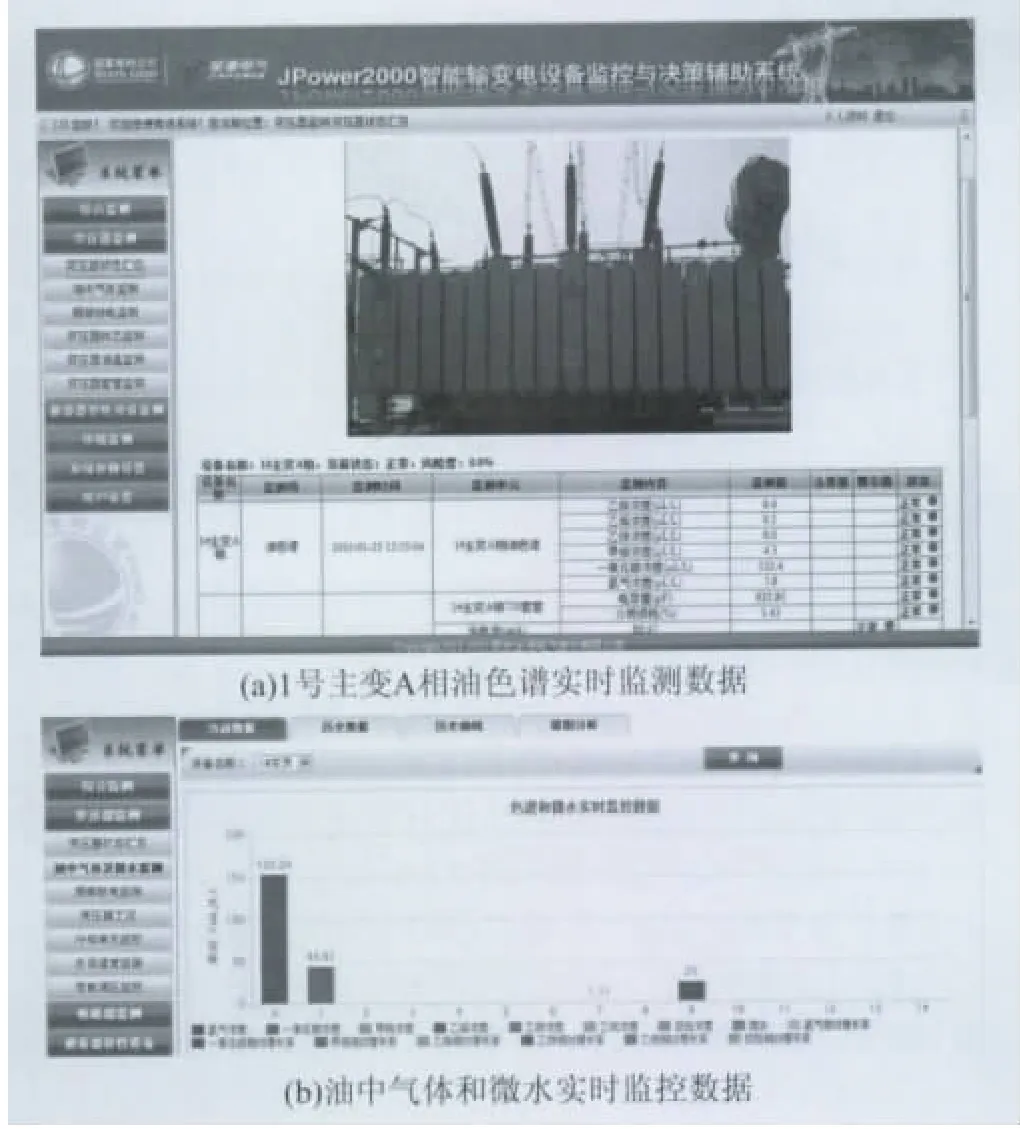
图3 油色谱实时数据Fig.3 Real-time data of DGA

3.2 测试数据的仿真结果

本文根据主变压器油色谱IED监测的运行数据，并收集具有典型特征的变压器故障数据共80组数据，以模糊化边界后的编码作为网络的输入，运用贝叶斯正则化方法改进的L-M算法对变压器运行状态进行诊断。本文所选的80组数据均包括5种特征气体及其对应的变压器运行状态。将所选数据中V(CH4)/V(H2)，V(C2H4)/V(C2H6)，V(C2H2)/V(C2H4)的比值作为输入量，代码“1”、“2”、“3”、“4”、“5”分别表示变压器“正常”、“中低温过热”、“高温过热”、“火花放电”、“电弧放电”等状态，将这5种运行状态作为输出量。选取80组数据中的70组作为网络的训练样本，剩余10组作为测试样本，进行仿真，结果如图4，5所示。

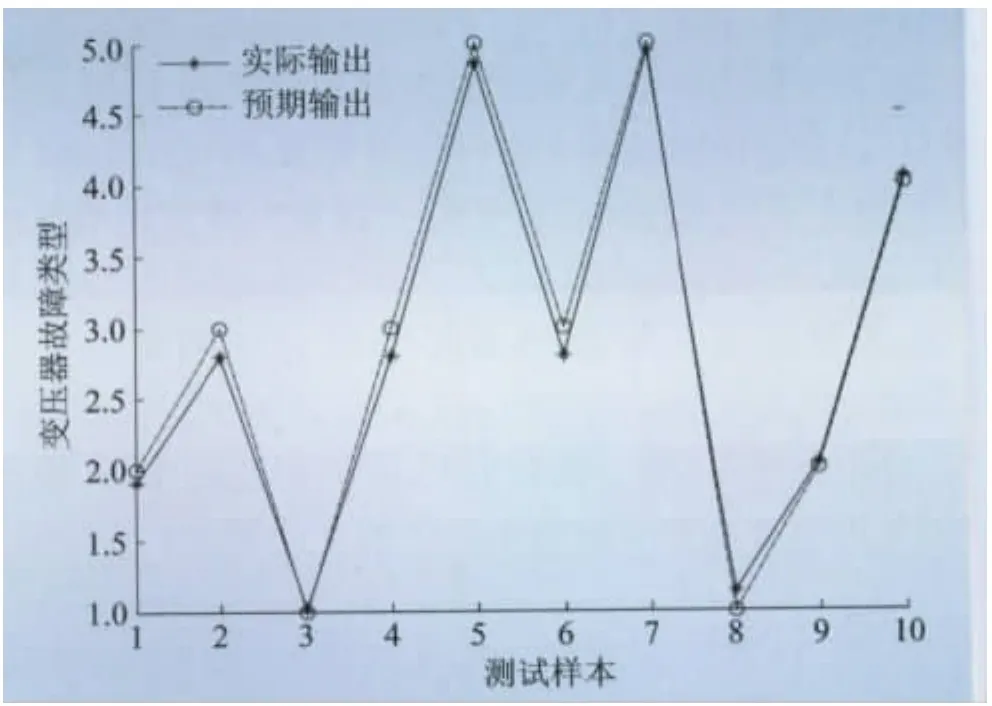
图4 基于贝叶斯正则化的L-M模型仿真结果Fig.4 Simulation results of L-M model based on Bayesian regularization

图5 基于模糊贝叶斯正则化的L-M模型仿真结果Fig.5 Simulation results of L-M model based on fuzzy Bayesian regularization

3.3 对比其他分析方法

为了进一步说明贝叶斯正则化的模糊L-M神经网络在变压器故障诊断中的优势，以10组测试样本为依据，现将它同以下几种预测方法进行对比分析，仿真对比见表1。

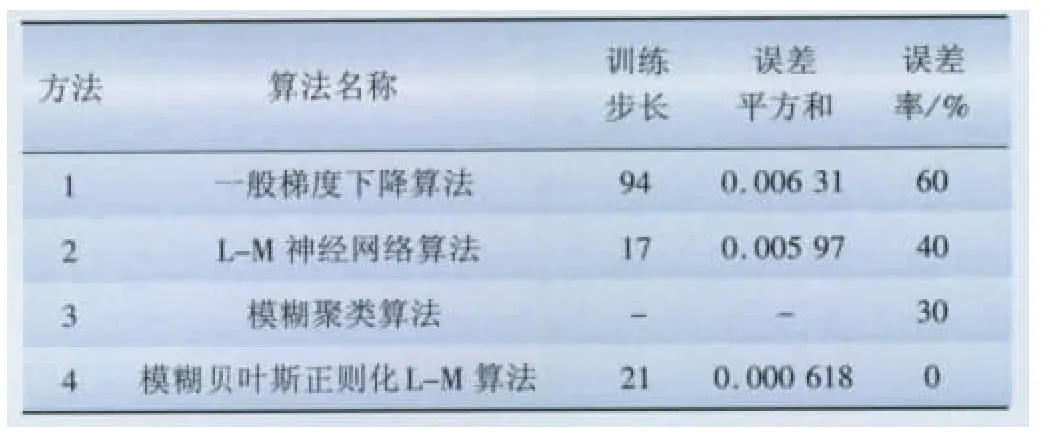
表1 仿真对比表Tab.1 Simulation comparison

由上述4种模型的变压器故障仿真结果可知:

(1)对比方法1和方法2的训练步长可知，由于BP网络是利用误差的反向传播不断调整权值的变化，因而计算冗长，在第94步才达到目标误差，而L-M算法通过在最速梯度下降法和高斯－牛顿法之间自适应的调整来优化网络权值，使其能够有效收敛，大大提高了网络的收敛速度，因此L-M网络的学习速度是BP网络所无法比拟的［14］;

(2)对比方法2和一般贝叶斯正则化L-M模型的仿真结果发现，基于L-M网络的模型在第17步就达到最小误差范围，训练速度比方法1快，然而其实际输出与预期输出在第5、6、7个测试样本处差距加大，甚至出现误判变压器的故障类型，而基于贝叶斯正则化的L-M模型的实际输出与预期输出趋势一致，泛化能力强;

(3)对比方法4和一般贝叶斯正则化L-M模型的仿真结果得出，基于模糊贝叶斯正则化的L-M模型，由于模糊化编码边界去除了原始气体数据的冗余信息使得训练速度远远优于贝叶斯正则化L-M模型，并且使得变压器的实际输出与预期输出完全吻合。

由此可见，基于模糊贝叶斯正则化的L-M模型是集训练速度与准确率于一体的优化算法。

4 结论

本文提出的基于贝叶斯正则化模糊L-M网络变压器故障诊断模型，仅经过21次训练就使网络误差达到了期望值，实际值与预测值的误差平方和仅为0.000 618，且拟合曲线光滑，预测效果明显优于一般的梯度下降法和L-M算法。

(1)该方法利用模糊理论将三比值法的边界编码模糊化，运用模糊分布的隶属度函数，克服了传统改良三比值编码过于绝对的缺陷。

(2)通过L-M算法使得网络每次迭代不再沿着单一的负梯度方向，而是允许误差沿着恶化的方向进行搜索，同时通过在最速梯度下降法和高斯－牛顿法之间自适应调整来优化网络权值。

(3)结合贝叶斯正则化L-M算法对权值进行训练，不仅汲取了L-M算法较快的收敛速度，而且弥补了其在过度拟合，预测效果不佳，对新数据预测不起作用等方面的不足。

通过实例分析得出，本方法能够快速、准确地诊断变压器的运行状况，同时能够使网络有效收敛、大大提高网络的收敛速度和泛化能力，在实际工程中得到了良好应用。

致 谢

本文中实验方案的制定和实验数据的测量记录工作是在金源电气集团有限公司舒佳、陈小雄等工作人员的大力支持下完成的，在此向他(她)们表示衷心的感谢。

［1］黄新波.变电设备在线监测与故障诊断［M］.北京:中国电力出版社，2008:13-18.

［2］廖怀东，李海威.变压器油色谱分析及故障判断［J］.电力建设，2003，24(10):25-29.

［3］周喜超，刘峻，郑伟.数学形态学融合多神经网络的变压器故障诊断［J］.电力建设，2009，30(1):38-40.

［4］彭宁云，文习山，陈江波，等.电力变压器BP神经网络故障诊断法的比较研究［J］.高压电器，2004，40(3):173-176.

［5］黄鞠铭，朱子述，胡文华，等.BP网络在基于DGA变压器故障诊断中的应用［J］.高电压技术，1996，22(2):21-23.

［6］王永强，律方成，李和明.基于贝叶斯网络和油中溶解气体分析的变压器故障诊断方法［J］.电工技术学报，2004，19(12):75-77.

［7］李林，万志聪.基于模糊三比值法的电力变压器绝缘故障诊断研究［J］.浙江电力，2011(2):12-14.

［8］程加堂，熊伟，徐绍坤.基于改进粒子群优化神经网络的电力变压器故障诊断［J］.高压电器，2012，48(2):42-45.

［9］贾嵘，徐其惠，李辉，等.基于邻域粒子群优化神经网络的变压器故障诊断［J］.高压电器，2008，44(1):8-10.

［10］潘翀，陈伟根，云玉新，等.基于遗传算法进化小波神经网络的电力变压器故障诊断［J］.电力系统自动化，2007，31(13):88-92.

［11］宋功益，郭清淘，涂福荣，等.模糊贝叶斯网的变压器故障诊断［J］.电力系统及其自动化学报，2012，24(2):103-105.

［12］张德丰.MATLAB神经网络应用设计［M］.北京:机械工业出版社，2009:107-113.

［13］魏星，舒乃秋，崔鹏程，等.基于改进PSO_BP神经网络和D_S证据理论的大型变压器故障综合诊断［J］.电力系统自动化，2006，30(7):46-50.

［14］王晓霞，王涛.基于粒子群算法优化神经网络的变压器故障诊断［J］.高电压技术，2008，34(11):2362-2367.