含风力－抽蓄发电的电力系统经济运行方式优化

吕项羽，李德鑫，郭欢，潘文霞，张程程

(1.国网吉林省电力有限公司电力科学研究院，长春市130021;2.国网江西省赣西供电公司，江西省新余市338025;3.河海大学能源与电气学院，南京市211100)

0引言

由于风电出力具有波动性、间歇性，风电并网运行必须由常规电源为其提供有功补偿，以满足系统的安全、稳定运行。因此，一般将风电作为负负荷，这种采用常规电源对负负荷进行跟踪即为风电“调峰”［1-2］。随着大规模风电并网运行，各地出现了不同程度的弃风现象。特别是在冬季供暖期间，热电机组并网更是加大了系统的调峰困难，直接影响了电网接纳风电能力［3］。系统调峰能力不足直接导致了大量风电在负荷低谷期间被限制出力，造成了巨大的经济损失与风电资源的浪费。因此，如何解决弃风，提高并网风电系统的调峰能力，具有重要的理论意义和实际价值。

由于风电功率波动较大，在风电并网后常常要求系统留有一定的正备用和负备用，以保证系统的稳定运行［4-5］。文献［6］提出了风电与火电协调调度，风电并网加大了火电机组的调度困难，存在大量弃风。文献［7］提出抽水蓄能系统(pumped hydro system，PHS)和风电、火电联合运行，引入风电最大注入功率约束限制风电出力，但没有考虑PHS的储能限制，也没考虑PHS的容量配置问题。文献［8］考虑了风电功率预测误差，通过优化常规火电机组运行确保风电全额上网，但是没有考虑机组的启停成本和启停时间约束。文献［9］提出了PHS和风电的效益模型，没有考虑系统中其他发电形式对调峰容量的影响。

从系统的角度看，风电的不可控性是对系统的最大威胁。为此，电网必须增加系统的调峰容量来应对风电对电网的冲击。而PHS的响应时间短，工况转换迅速，是削峰填谷的理想调峰电源。本文从提高风电利用率、减少弃风的应用背景出发，研究在并网风电系统中配置PHS，提高系统接纳风电能力的可行性。以系统的运行成本最小为目标，采用实数编码的遗传算法优化含风力－抽蓄发电的电力系统运行，合理安排系统中各机组的工作位置。通过对含风力－抽蓄发电的电力系统经济运行进行研究，结合系统分别不同峰谷电价比和热电机组比例时的运行情况及各项评价指标，确定合理的装机容量及水库的存储容量，为并网风电系统提供有效的抽水蓄能电站配置参考方案，以期最大程度地利用风电，达到合理利用资金成本，优化资源配置的目的。

1 含风力－抽蓄发电的电力系统数学模型及运行优化

1.1 数学模型

在含有风电、火电、热电、PHS机组的系统中，PHS主要承担的任务是:(1)储存弃风。系统存在弃风时，采用PHS抽水储存多余风电，在电网有需要的时候释放。PHS储存电网不需要的弃风时没有抽水成本，只需要让风场同意送电。(2)调峰填谷，减少风电的间歇性和波动性对火电机组出力的影响。本文中电厂运行成本仅包括维持电厂运行所需购买燃料的费用，不包括年运行维护费用。一般认为风电和PHS联合运行没有运行成本，因此，整个系统只考虑火电及热电机组的运行成本，以系统的运行成本最小为优化原则建立目标函数［10-11］。

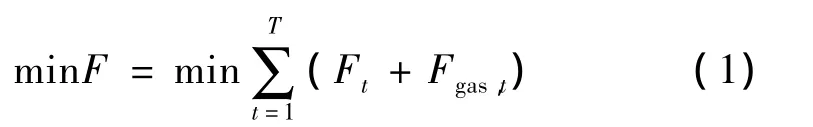
式中:F为系统的运行成本;T为系统运行周期;Fgas，t为热电机组的运行成本;Ft为火电机组的运行成本，其计算公式为

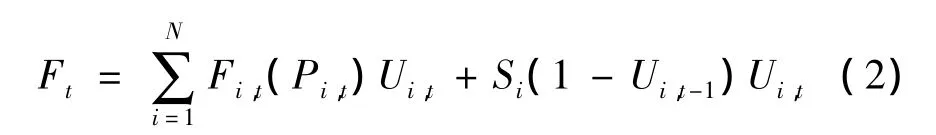
式中:N为火电机组数量;Pi，t为火电机组i在时段t的有功出力;Ui，t为机组i在时段t的启停状态，0表示停机，1 表示运行;Fi，t(Pi，t)、Si分别为火电机组 i在时段t的发电成本、启动成本，其计算公式为

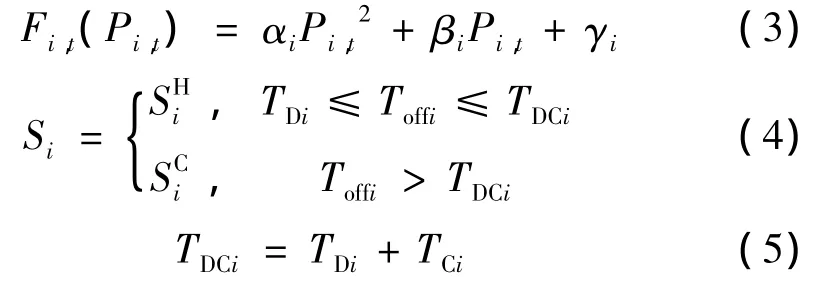
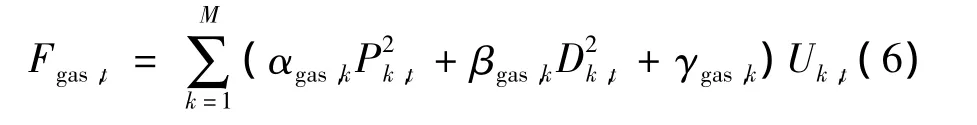
式中:M 为热电机组的组合数量;Pk，t、Dk，t为热电机组k输出的有功功率、供热量;Uk，t为机组k在时段t的启停状态;αi、βi、γi、αgas，k、βgas，k、γgas，k为常系数。

系统约束条件如下:

(1)系统需求约束为

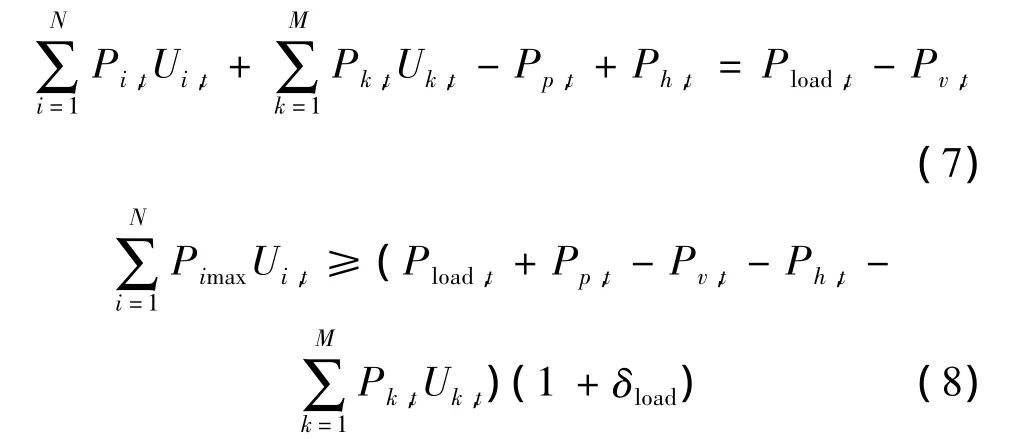
式中:Pload，t为时段 t的系统负荷;Pp，t、Ph，t为 PHS 的抽水功率、发电功率;Pv，t为时段t的预测可利用风电功率;δload为负荷对备用的贡献。式(7)描述了系统中火电、热电、风电、PHS的出力必须满足电网电力平衡;式(8)为系统的备用约束。

(2)火电机组约束为

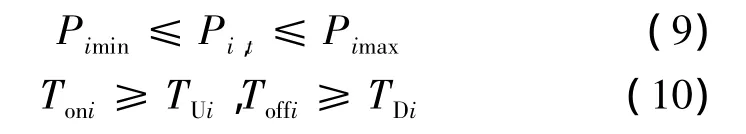
式中Pimax、Pimin分别为机组i的最大、最小有功出力;Toni为机组i的实际连续运行时间;TUi为机组i的最小持续开机时间。式(9)、(10)为火电机组的出力约束、连续启停时间约束。

(3)热电联产机组运行约束

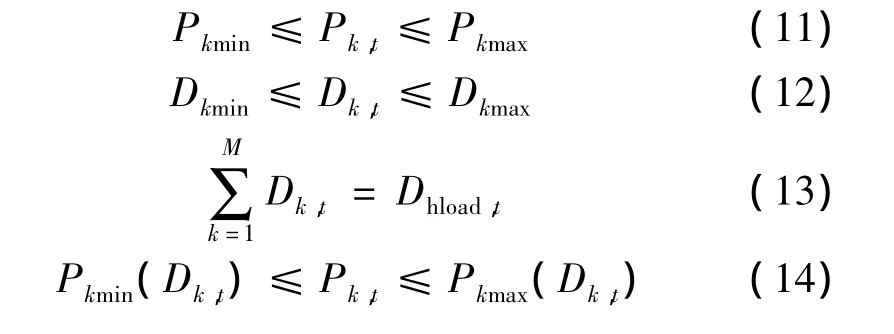
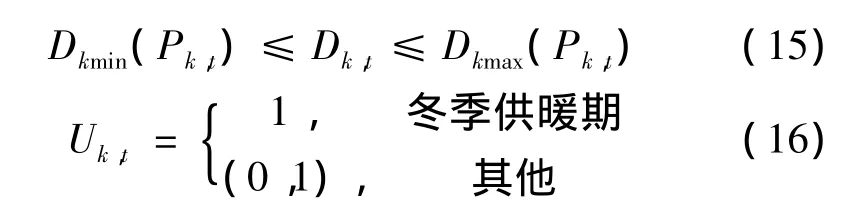
式中:Dhload，t为系统的热负荷需求;Pkmin、Pkmax分别为机组k的最大、最小有功出力;Dkmin、Dkmax分别为机组k 的最大、最小供热量;Pkmax(Dk，t)、Pkmin(Dk，t)为在一定供热状态下，对应的发电限制的上下限;Dkmax(Pk，t)、Dkmin(Pk，t)为在一定电负荷状态下，对应的供热量的上下限。式(11)、(12)分别为热电机组的发电和供热约束，式(13)表示所有供热机组的供热量必须满足用户的热负荷需求，式(14)、(15)描述了供热机组的热、电负荷之间相互制约的关系。式(16)为热电机组的启停状态约束，在冬季时段，热电机组不能关停，非供暖期间则视具体情况而定。

(4)PHS机组约束

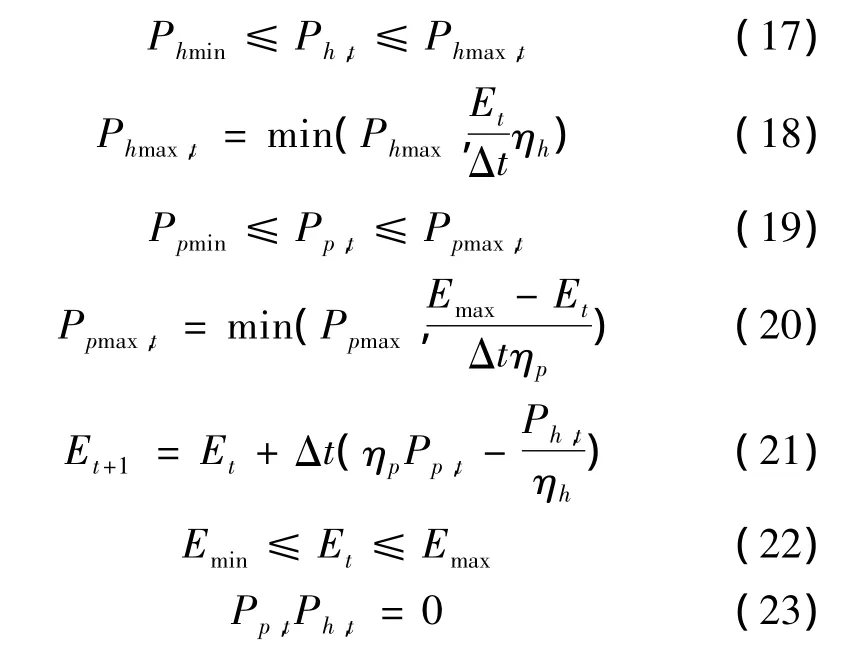
式中:Ppmax，t、Ppmin分别为水泵的最大、最小功率;Phmax，t、Phmin分别为水轮机的最大、最小功率;Emin、Emax、Et分别为PHS水库的最小储能值，最大储能和t时段的储能;ηp、ηh分别为PHS的抽水效率、发电效率;Δt为每个时段的时长。式(17)～(20)为PHS的发电和抽水功率限制;式(21)、(22)为PHS的水库的存储容量限制，文中将PHS中水库的储水容量用电量表示，因此水库的库容可以用PHS的储存的电能表示;式(23)表示PHS在同一时段只能有1个工况。

(5)风力发电场约束

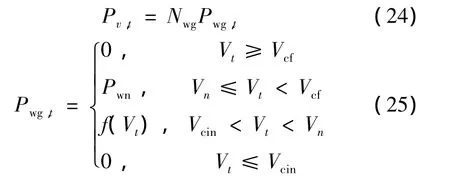
式中:Nwg为风力发电机数目;Pwg，t为风电机在时段t的预测可利用风电功率;Pwn为风机的额定功率;Vt为时段 t的预测风速;Vcin、Vcf为切入、切出风速;为常系数。式(24)、(25)为风场输出功率，不考虑风电机组的同时率。

1.2 应用遗传算法优化系统经济运行

遗传算法(genetic algorithms，GA)结合了计算机科学与进化论思想，利用计算机的强大计算搜索能力，模拟生物进化遗传机制，是一种全局优化概率随机搜索算法，在电力系统中得到了广泛应用。本文采用实数编码的GA，在遗传操作过程中对个体进行调整使之满足各约束条件，并选取了适合本文的适应度函数，从而减小搜索空间，提高搜索效率。具体步骤如下:

(1)整理原始数据。包括负荷及风速风机特性，PHS的参数及系统内火电、热电机组的数据等。

(2)本文采用实数编码，染色体长度根据研究时段内系统中火电机组数量和PHS的抽水发电工况确定。根据预测风速计算风电场的输出功率，随机生成初始种群。种群中每个个体染色体长度为N+Q+P+2P，其中N为火电机组的组合数量，Q为热电机组的组合数量，P为PHS的工况数量，2P为PHS水轮机输出的有功功率和水泵抽水机组的组合数量。在火电机组、热电机组开停机情况和PHS的工况确定后，火电机组和热电机组的出力按等耗量微增率准则确定。

(3)个体调整方法。为保证种群具有良好的特性，根据系统中不同的约束条件，采用不同的处理方法，使得每个个体均满足各项约束。

1)对于火电机组的连续启停时间约束，按以下策略进行修正。首先对于机组i的连续启动、停运时间进行判断，如果满足约束条件，则不需要进行修正;如果不满足约束条件，则延长机组i的启动、停运时间，直到满足最小启动、停运时间约束为止。

2)对于系统的旋转备用约束，按以下策略进行修正。当t时段的开机机组最大出力之和小于系统的负荷和备用需求之和时，首先检查当前解中t时段是否有停运机组。如果没有则终止修正;如果有，则从停运机组中选择一台机组改为开机，此时不能违背机组的连续启停时间约束。

3)多余机组检查。如果某些时段有过多机组投入运行，例如某时段所有机组都开机，虽然满足约束条件但是不经济也不合理，这时要对多余机组进行修正，关闭多余机组［12］。同时，不能违背机组的连续启停时间约束。

(4)计算目标函数时，首先检验个体是否满足所有约束条件。当个体不满足约束时，则目标函数值F返回1个较大的惩罚值;如果满足所有约束，则计算运行成本得出目标函数值。为了使得PHS尽量在负荷低谷时抽水，在负荷高峰期间发电，引入PHS的惩罚费用系数，评价函数由目标函数转换，其表达式为

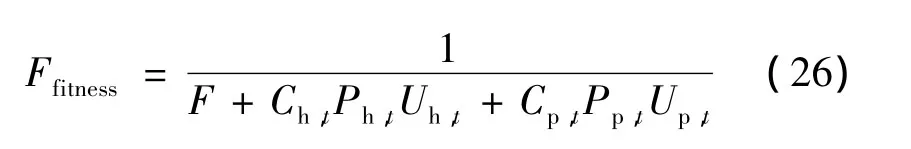
式中:Cp，t为抽水惩罚系数;Ch，t为发电惩罚系数，其计算公式为

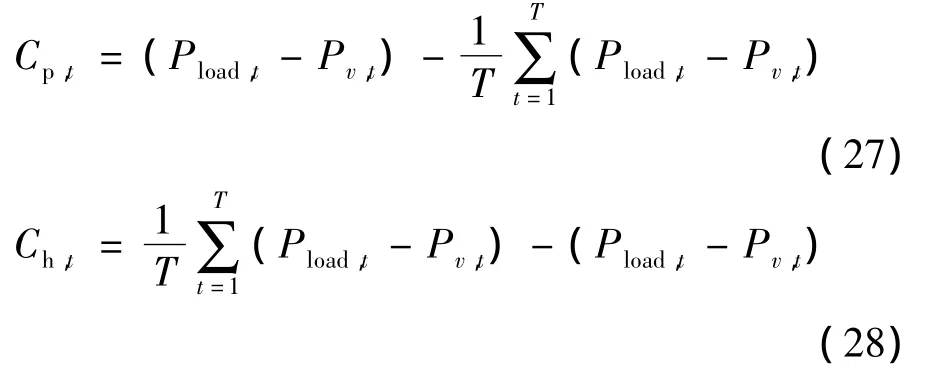
当抽水惩罚系数和发电惩罚系数小于或等于0时，PHS的虚拟运行费用可以减小系统成本;且发电惩罚系数和抽水惩罚系数越小，适应度函数越大。这样能够使得PHS在满足约束条件的情况下尽可能在峰谷时段工作，减少火电机组出力的频繁调整，降低系统的运行成本费用，提高搜索效率。

(5)保存种群中最大适应度值对应的个体，然后按选择、精英保存、交叉和变异等步骤进行遗传操作实现种群的不断进化，直到满足迭代次数，得到全局最优解。

2 算例分析

2.1 评价指标

本文主要从系统的运行成本、PHS的单位净利润Pprofit、净负荷峰谷差变化率 σn来评价系统运行的效果。

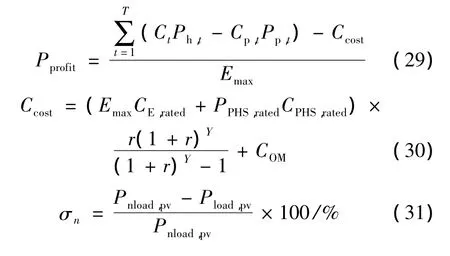
式中:Ct为t时刻的上网电价;Cp，t为t时刻的抽水费用;Ccost为PHS的投资成本费用;CE，rated为PHS的能量费用;CPHS，rated为PHS的功率费用;COM为运行维护费用;r为社会折现率;Y为 PHS的生产使用年限;Pnload，pv为等效负荷的峰谷差，将风电作为负负荷处理，系统负荷减去风电为等效负荷;Pload，pv为净负荷峰谷差，等效负荷减去PHS的发电及抽水功率即为净负荷。PHS的造价成本包括固定投资成本和运行维护费用;固定投资成本包括能量成本和功率成本;能量成本包括系统的电力变换设备和系统中的一些辅助设备费用，与PHS的水库的存储容量即储能上限成正比;功率成本与PHS的额定功率成正比［13］。

2.2 基础数据资料

火电机组采用IEEE10机系统，美元兑人民币的汇率为1美元兑换6元人民币，火电机组参数见文献［14］。系统中有250台额定功率为1MW的风机，采用Matlab7.0中的双馈感应风力机数据，其风速－功率特性如图1所示。PHS的固定投资成本包括能量费用72元/(kW·h)和功率费用3 000元/kW［13］。年运行维护费用为成本投入的5%，生产期按50年计。抽水费用为上网电价的0.5倍［14］。

冬季供暖期(11月至次年3月)供热机组采用以热定电的运行方式［15］，首先满足热负荷需求，剩余汽量用来发电。2台热电机组参数见文献［16］，其中标煤成本为300元/t。为保持系统总容量不变，热电机组并网后，停开2号火电机组，增加1台10号火电机组。热负荷参数详见文献［17］，其他参数见文献［18-19］。系统总装机容量为2 302MW，包含1 652MW火电机组、250MW热电机组和400MW热电机组。

本文的优化时间段取为24 h，上网电价采用“峰谷平”三段电价，高峰时段(07:00～11:00和17:00～21:00)电价为 0.75元/(kW·h)，平峰时段(11:00～17:00和 21:00～23:00)电价为 0.5元/(kW·h)，低谷时段(00:00～07:00和23:00～24:00)电价为0.25元/(kW·h)。由于式(30)为年成本，本算例分析的时间段为1天，即式(29)中的T为1天，故式(30)要除以365。

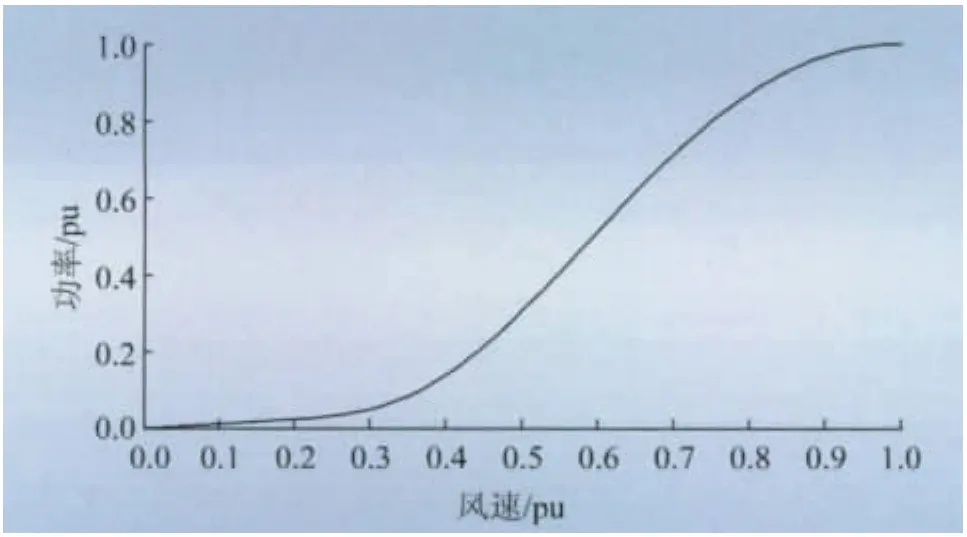
图1 风电机风速－功率特性曲线Fig.1 Wind speed and power characteristic curve of wind turbine

2.3 仿真结果

向系统中分别加入不同容量的PHS，对应的水库存储容量为PHS的额定功率下持续工作3 h，研究系统中热电机组比例分别为0%、20%和50%时的运行情况。

对于热电机组而言，必须先满足热负荷要求。首先采用等微增率法对热负荷进行分配。当热电机组的热负荷达到一定值时，往往不能满出力发电。图2所示为系统负荷。由图2可知，2号机组在供热量达到最大时，能够发出的有功功率最大值仅为170MW，几乎不能调整出力。1号机组出力调整范围大约在额定容量的70% ～90%，可调整范围很小。如果热电机组比例为0%时，不含PHS时火电机组的最低出力为300MW;热电机组比例为20%时，不含PHS时常规机组(包括火电、热电)的最低出力为479～499MW，由此可见系统的最低出力变大了。这意味着，系统接纳风电的空间变小了。热电机组在系统中比例提高到50%，不含PHS时常规机组的最低出力为653～693MW，此时为02:00～04:00时段，可利用风电功率加上常规机组的最小出力之和大于系统负荷，因此不得不对风电采取限制措施。

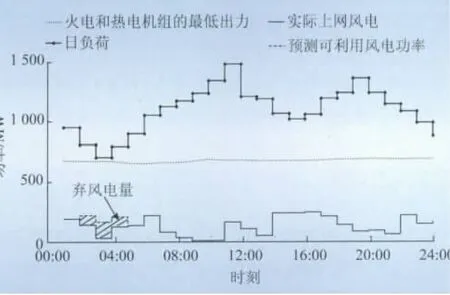
图2 系统中日负荷情况Fig.2 Daily load of power system

含风力－抽蓄发电的电力系统运行成本如图3所示，通过非线性拟合得到了系统的运行成本和PHS容量的关系曲线。

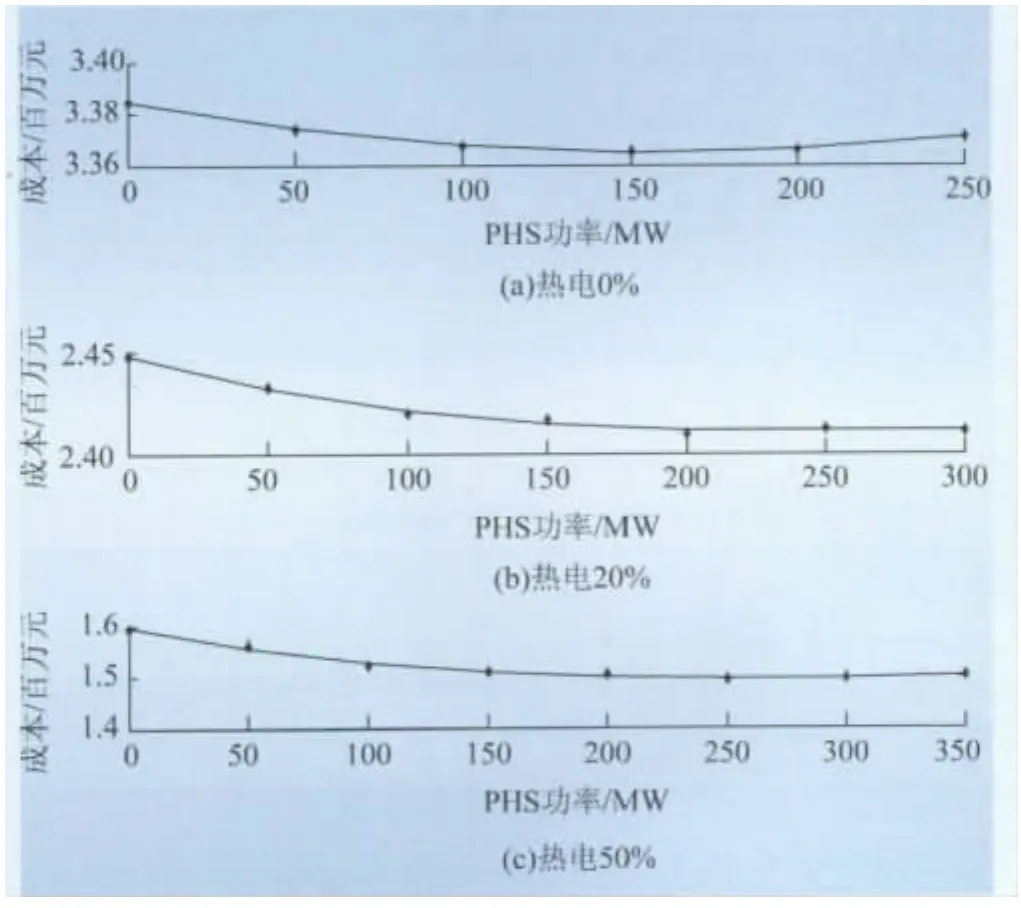
图3 系统中热电机组比例不同时的系统运行成本Fig.3 System operation costs with different proportions of thermal power

由图3可知，当PHS容量适当时，加入PHS后系统的运行成本明显减少。若系统中无热电机组，PHS容量为150MW时，系统的运行成本最小。热电机组比例为20%时，PHS容量为200MW时，系统的运行成本最小。热电机组比例为50%时，PHS容量达到150MW时，系统的弃风电量为0;PHS容量达到250MW时，系统的运行成本最小。系统加入了热电机组后，对PHS的容量需求也越来越大。而当PHS大于某一功率时，PHS是利用系统中的富余电能抽水。当PHS的容量过大时，为了充分利用PHS容量会发生过充的情况，增加系统的运行成本，具体如表1所示。

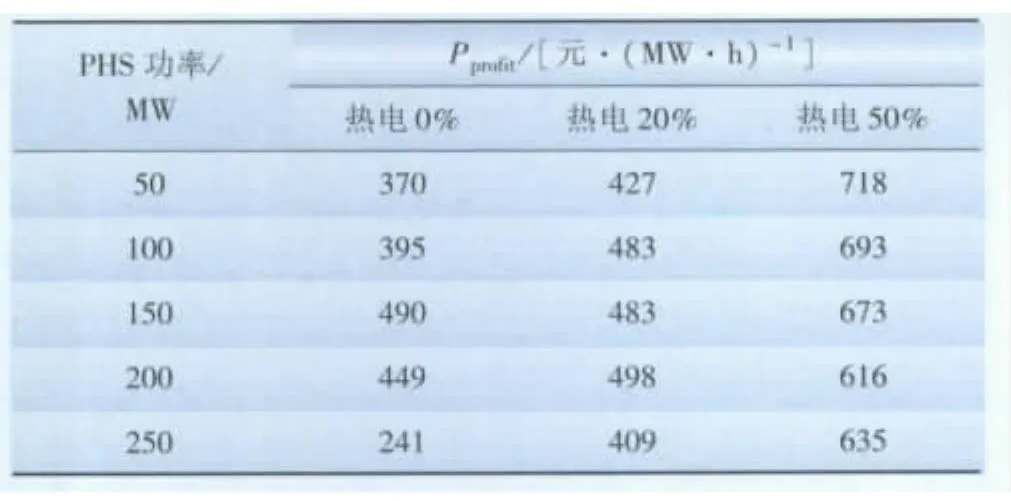
表1 系统中热电机组比例不同时PHS的单位净利润Tab.1 Net profit of PHS with different proportions of thermal power

从表1可看出，在并网风电系统中配置PHS可以获得经济效益，系统中热电机组比例越高，PHS的净利润越大，说明在含有热电机组时PHS的利用率更高。加入热电机组后PHS的效益变化明显，这是由于热电机组加入后，系统的向下调整容量减少了，系统接纳风电的空间变小了。因此能够为PHS提供更多的低谷抽水功率。

当系统中无热电机组时，PHS容量为150MW时的净利润最高;热电机组比例为20%时，PHS容量为200MW时的净利润最高;热电机组比例为50%时，PHS容量越小，净利润越大，此时PHS的净利润随着容量的增加反而减小了。这是由于热电比例为50%时系统存在弃风，PHS储存弃风时没有抽水成本。并且系统中机组的开机情况发生了变化，PHS在平峰时段(12:00～17:00)，可抽水容量减小了，PHS的日利用率减小了，所以净利润变小了，经济效益减少了。此时受到PHS造价的影响，PHS的容量越小则其经济效益越好。值得注意的是，PHS容量为200MW时的净利润小于PHS容量为250MW的净利润，这是由于PHS容量为200MW时在22:00～24:00时段也抽水了的缘故。

σn表示系统的净负荷峰谷差变化率，这个值为正值，则说明系统的峰谷差变小了，如果为负值，说明系统的峰谷差变大了。热电机组比例变化时的σn数据如表2所示。由表2可知:无PHS时，系统的σn为负值，表明风电加大了系统的峰谷差，风电呈现了反调峰特性;在同一热电比例下，随着PHS容量的增加，σn越来越大，净负荷峰谷差越来越小，PHS有效地降低了系统的峰谷差;PHS容量相同时，当热电机组比例增加时，σn变化不大。值得注意的是，PHS容量为250MW时，系统中热电比例为0%时的σn远小于热电比例为20%和热电比例为50%时的σn。系统中无热电机组时，需要的调峰容量更少。但是PHS容量过大时，为充分利用PHS，有时在高峰时段抽水太多发生过调峰现象。

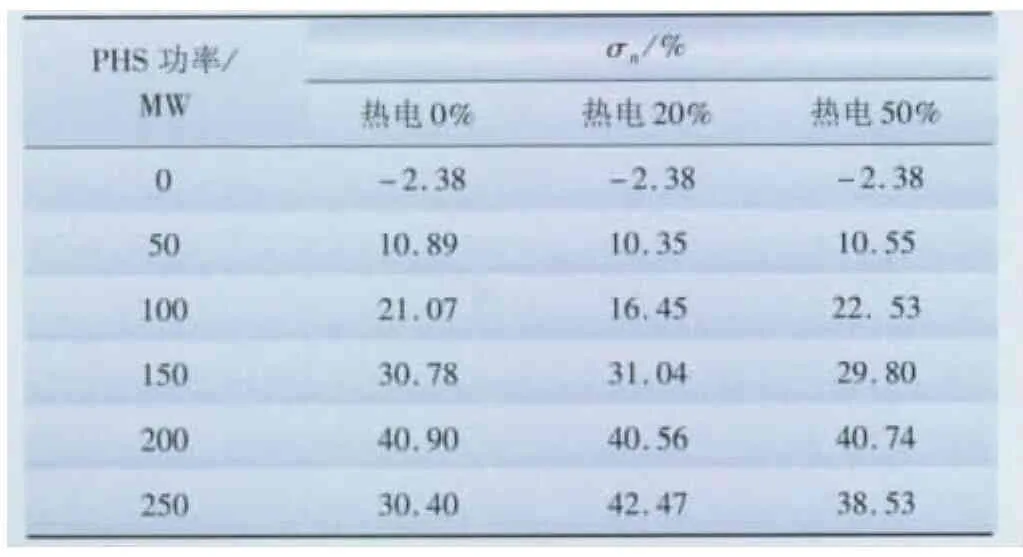
表2 系统中热电机组比例不同时的净负荷峰谷差变化率Tab.2 Change rate of net load peak valley difference with different proportions of thermal power

综合表1、2可知，系统的净负荷峰谷差变化率在抽水蓄能为200MW时达到最大值。图4为抽水蓄能容量分别为150、200MW时的日运行情况，负值表示抽水蓄能电站处于抽水工况。由图4可得，抽水蓄能为200MW时在第8和18时段没有达到储能上限，而150MW可以达到储能上限，可以看出PHS容量为150MW更能充分利用储能资源。

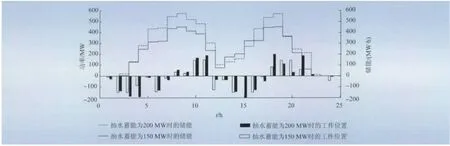
图4 PHS充放电曲线Fig.4 PHS charging and discharging curves

综合表1、2和图4可得:当系统中无热电机组时，PHS容量为150MW时各项评价指标最优;当系统中热电比例为20%时，PHS容量为200MW时各项评价指标最优;当系统中热电比例为50%时，PHS的净利润最大时的PHS容量和系统运行成最小时的PHS容量并不一致。可见，当系统中热电比例越高，系统对PHS的容量需求越大。

2.4 PHS的水库存储容量

当系统中热电机组比例为20%时，PHS容量为200MW时各项评价指标最优。为此，研究系统中热电比例为20%时PHS的最优水库存储容量。将PHS的水库中水的容量用水库储存的电能表示，水库库容的变化等效于水库中储能如图5所示，单位净利润如表3所示。PHS的储能上限表示PHS在额定功率下的持续放电时间，PHS在额定功率为150，200MW，对应的水库存储容量可以持续放电1，2，3，4 h时系统的运行情况，其他参数保持不变。

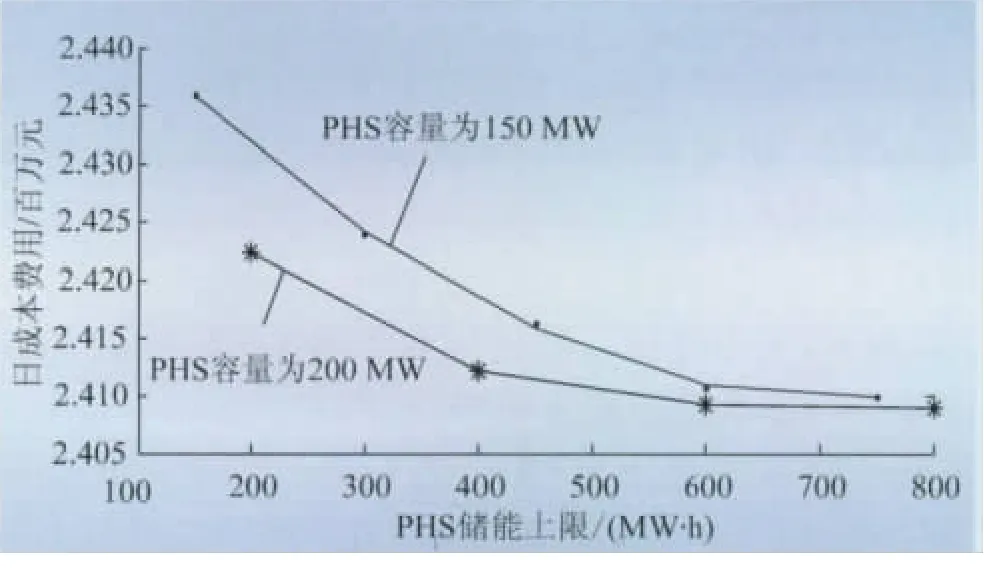
图5 PHS水库存储容量不同时系统的日成本费用Fig.5 Daily cost of the system when PHS reservoir storage capacity is different

由图5和表3可看出，随着PHS水库存储容量的提高，系统的运行成本也逐渐减少，PHS的水库存储容量达到600MW·h以后，系统的运行成本和PHS的净利润不再变优。PHS的额定功率为150、200MW时，持续放电时间为1 h时，此时PHS的净利润为负值。当PHS的功率相同时，水库存储容量越高，则其净利润越高，PHS容量为150MW 时，水库存储容量达到450MW·h，净利润最大;PHS为200MW时时水库存储容量达到600MW·h，净利润最大。

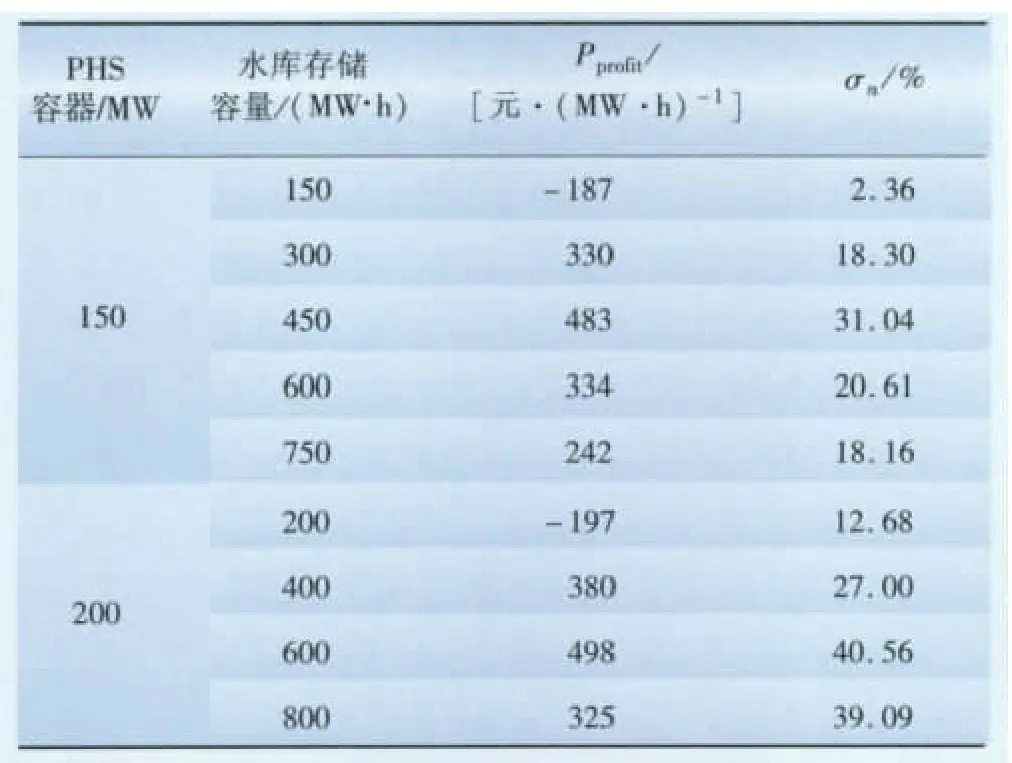
表3 PHS水库存储容量不同时的单位净利润Tab.3 Net profit of PHS when PHS reservoir storage capacity is different

综合表1、3可知:当水库存储容量相同时，如果PHS在额定功率下持续放电时间小于等于3 h时，PHS的额定功率越小的，则其净利润和σn越大;如果额定功率下的持续放电时间大于等于3 h时，功率越大，净利润和σn越大，这是由于PHS受造价的影响突出。PHS的造价主要分为与功率相关的功率成本和与储能相关的能量成本，并且功率成本约占造价成本的90%。所以，PHS库容的大小对其经济效益影响显著，并且PHS的库容不能太小，否则难以补偿投入的固定成本。

由图4、5可知:当水库存储容量相同时，PHS的功率越大，则系统的运行成本越低。这是由于PHS在高峰时段的发电功率高，可以减少调峰机组在高峰时段的开机次数。综上，PHS的最优容量为200MW，水库存储容量达到600MW·h，此时PHS容量约占系统总容量的9.4%。

2.5 峰谷电价比对PHS的影响

在表1中，PHS的单位净利润是采用峰谷电价比为3∶1计算的。如果改变峰谷电价比，即在平段电价的基础上按比例上下浮动，计算系统中无热电机组时PHS的单位净利润结果如表4所示。

由表4可看出:在峰谷电价比为1∶1时，PHS的单位净利润为负值，此时PHS的收入不足以支付PHS的造价成本。当峰谷电价比提高到1.25∶1时，PHS容量为50MW时，PHS的单位净利润为0.2元/(MW·h)，刚好达到盈利;PHS容量升高到250MW时，PHS的单位净利润出现负增长，此时PHS的收入不足以回收PHS的造价成本。当峰谷电价比为1.5∶1时，PHS容量小于250MW 时，PHS的单位净利润均为正值;PHS容量为250MW时，PHS的单位净利润为负值。峰谷电价比为2∶1及3∶1时，PHS的单位净利润均为正值。

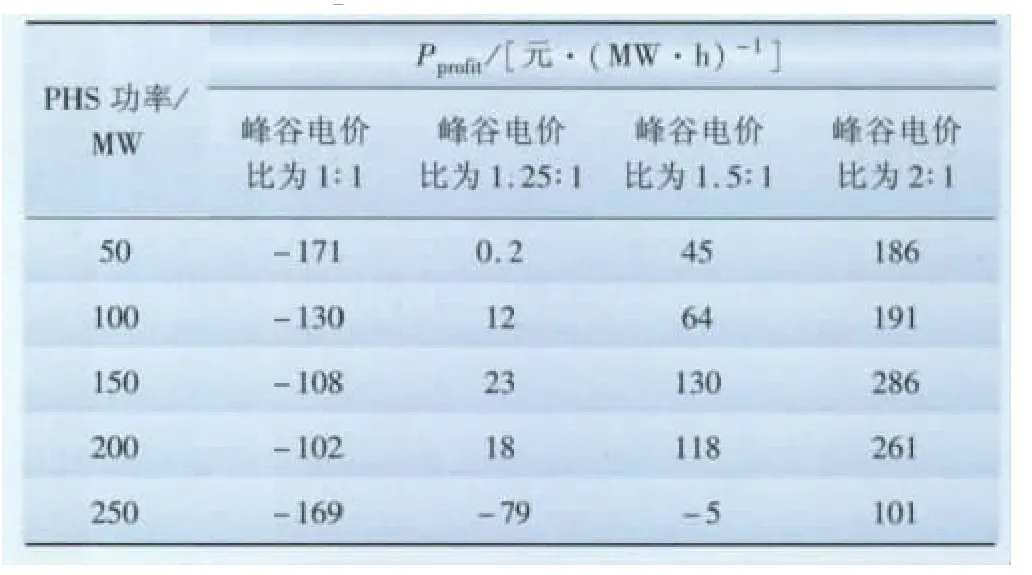
表4 系统中无热电机组时PHS的单位净利润Tab.4 Net profit of PHS without thermal units

3 结论

(1)PHS的造价中功率成本约占总造价的90%。受到PHS造价的影响，PHS的功率比水库存储容量对其的经济效益影响更大。PHS的水库存储容量不宜过小，PHS额定功率为150MW时水库存储容量为150MW·h，PHS额定功率为200MW时水库存储容量为200MW·h，即占总容量的7.2%和9.4%时，经济效益为负值，不能盈利。受到PHS造价的影响，只有峰谷电价比达到一定比率时，PHS提供的功能才能获得回报。文中峰谷电价比必须达到1.25∶1时PHS才能实现盈利。并且此时PHS容量不能太大，当 PHS容量为250MW，约占系统总容量的11.5%时的经济效益仍然为负值，不能盈利。

(2)系统存在弃风时，PHS的容量配置必须从系统的运行需求和PHS的经济效益这2个方面考虑。热电机组比例提高到50%时，系统存在弃风。此时系统的运行成本最小时的PHS容量占总容量的11.5%，而PHS的容量越小，其经济效益越好。

(3)对PHS的容量进行优化配置时需要综合考虑系统的机组的组成、负荷及风电出力、PHS的造价和整个系统的经济运行等多方面的影响因素。通过对该系统的经济运行分析，综合分析各项技术经济指标，得到该系统中抽水蓄能电站的最优容量为200MW，水库存储容量为600MW·h，占总容量的9.4%。

［1］衣立东，朱敏奕，魏磊，等.风电并网后西北电网调峰能力的计算方法［J］.电网技术，2010，34(2):129-132.

［2］张宁，周天睿，段长刚，等.大规模风电场接入对电力系统调峰的影响［J］.电网技术，2010，34(1):152-158.

［3］白阳，曾庆枫.大规模风电接入后在冬季供热方式下电网的控制方式［J］.电力技术，2010，19(10):1-7.

［4］王芝茗，苏安龙，鲁顺.基于电力平衡的辽宁电网接纳风电能力分析［J］.电力系统自动化，2010，34(3):86-90.

［5］侯佑华，房大中，白永祥，等.大规模风电运行的调度模式设计［J］.中国电力，2010，43(8):67-72.

［6］Ummels B C，Gibescum，Pelgrum E，et al.Impacts of wind power on thermal generation unit commitment and dispatch［J］.IEEE Transactions on Energy Conversion，2007，22(1):44-51.

［7］张鹏，刘继春，吕林，等.基于风蓄协调的节能调度方法［J］.电力系统保护与控制，2011，39(2):29-34.

［8］周玮，彭昱，孙辉，等.含风电场的电力系统动态经济调度［J］.中国电机工程学报，2009，29(25):13-18.

［9］García-González J，de la Muela Rm R，Santos Lm，et al.Stochastic joint optimization of wind generation and pumped-storage units in an electricity market［J］.IEEE Transactions on power systems，2008，23(2):460-468.

［10］杨俊杰，周建中，喻菁，等.一种求解大规模机组组合问题的混合智能遗传算法［J］.电网技术，2004，28(19):47-50.

［11］潘文霞，范永威，朱丽，等.风电场中抽水蓄能系统容量的优化选择［J］.电工技术学报，2008，23(3):120-124.

［12］高山，单渊达.遗传算法搜索优化及其在机组启停中的应用［J］.中国电机工程学报，2001，3(3):45-48.

［13］Schoenung Sm，Hassenzahl W.Long vs.short-term energy storage:Sensitivity analysis［R］.New Mexico:Sandia National Laboratories，2007.

［14］夏澍.基于差分进化算法的含风电场电力系统动态经济调度［D］.北京:华北电力大学，2010.

［15］林章岁，罗利群.福建省风电出力特性及其对电网的影响分析［J］.电力建设，2011，32(12):18-23

［16］李冬.基于厂级调度的热电负荷优化分配系统的研究［D］.北京:华北电力大学，2010.

［17］许明子.基于粒子群算法的供热负荷组合预测［D］.大庆:东北石油大学，2011.

［18］刘勇.河北南网负荷特性分析与负荷预测研究［D］.北京:华北电力大学，2007.

［19］Lee T Y.Short term hydroelectric power system scheduling with wind turbine generators using the multi-pass iteration particle swarm optimization approach［J］.Energy Conversion and Management，2008，49(4):751-760.

［20］赵士和.抽水蓄能电站上网电价现状与展望［J］.电力技术经济，2004，16(2):36-38.

［21］杨晓东，石建，刘峻，等.“十二五”期间大规模风电接入对福建电网的影响及对策分析［J］.电力建设，2012，33(7):9-13.