管材弯曲回弹对内高压成形的影响及补偿方法

张伟玮，韩 聪，谢文才，苑世剑

(1.哈尔滨工业大学材料科学与工程学院，150090哈尔滨;2.一汽轿车股份有限公司，130012长春)

考虑到承载的强度和刚度因素，现代汽车构件如车架纵梁、发动机支架、顶盖纵梁、后桥车架、仪表盘等均是典型的三维曲线异性截面空心结构件［1-3］.内高压成形技术已经广泛应用以上构件的生产中，与冲压件焊接件相比，质量轻，生产成本降低、模具造价降低、抗弯扭能力高［4-6］.此类零件的成形往往包括CNC弯曲、预成形、内高压成形等几道工序.数控弯曲主要将零件的轴线变为二维或三维曲线，预成形则是合理的分配坯料，使零件在内高压成形过程中变形均匀，避免皱纹和破裂缺陷.

管材数控弯曲卸载后会产生严重的回弹，直接影响构件的尺寸精度，以及与其他构件的连接或装配［7-8］.对于轴线为三维的数控弯曲管件，回弹会导致随后工序的预成形和内高压成形中产生起皱或者破裂等缺陷.如果不能充分掌握数控弯曲过程管材的回弹规律，就要通过反复尝试各种工艺参数来调整零件形状来避免缺陷，提高生产成本，延长生产周期.

由于管材数控弯曲过程是一个几何非线性、材料非线性、接触非线性的复杂过程，同时又是一个多模具协同约束的过程.如果把以上所有因素都考虑在内，就很难通过解析解来精确表达回弹规律.近些年国内外许多学者都尝试通过有限元法，建立工艺参数对回弹影响的线性回归模型.Qureshi等［9］在平面应变条件下推导了铝合金薄壁管纯弯下的回弹解析模型，同时忽略截面畸和材料的包辛格效应.Murata等［10］通过有限元法得出结论，发现硬化指数对铝合金压弯回弹几乎没有影响.然而，对于工程问题，可以简化约束条件，建立简明的数学模型和材料模型，给出回弹角变化规律并作为补偿量应用在实际生产中.本文首先建立管材塑性弯曲理论模型［11］以及材料的弹塑性线性强化模型，通过理论解析得到弯曲回弹量表达式;其次通过实验得到不同弯曲角度下回弹量的统计数据并进行线性拟合，同时与理论模型进行对比;最后将回弹量作为补偿量应用到副车架内高压成形中.

1 研究对象

本文研究对象为汽车副车架，它是支撑前后车桥、悬挂的支架，图1所示为副车架的三维图形，轴线和截面均沿空间变化，结构较复杂，生产时通常采用一模两件的内高压成形工艺.

图1 副车架三维造型

其主要成形工序为数控弯曲、预成形和内高压成形.管材数控弯曲角度如图2所示.为了避免预成形和内高压成形过程产生缺陷，数控弯曲过程需要考虑卸载后管材回弹问题，得出回弹量与弯曲角之间的变化规律，并把回弹量作为补偿量来修正数控弯曲角度.

图2 管材数控弯曲角度

2 弯曲回弹量的理论计算

管材在力矩M作用下产生弯曲，弯曲过程内外层受力状态弯曲不同，外层减薄，内层增厚．其3个方向的应力分别为:切向应力σθ，圆周方向应力σφ，壁厚方向应力σt．具体受力示意图见图3．

图3 管材弯曲变形示意

以上弯曲理论模型的建立需要满足以下基本条件:

1)弯曲过程为纯弯曲且不发生截面扁化;

2)应力中性层与应变中性层重合;

3)管材管径不变，即圆周方向应变εφ=0;

4)管材按薄壁管假设，即壁厚方向应力σt=0．

假设中性层处曲率半径为ρ，弯曲角为α，则距离中性层y处的切应变εθ为

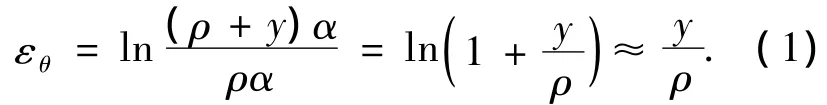
根据力矩平衡原理，管材外加弯矩M的大小应等于其切向应力σθ产生的弯矩之和，故弯曲力矩M为

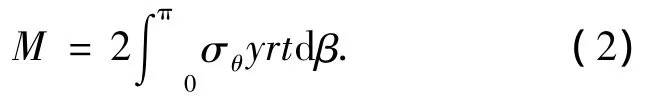
式中:y=rsin β;t为管材初始壁厚;r为管材初始外径．

材料的应力-应变模型为弹塑性线性强化模型，如图4所示，其基本表达式为

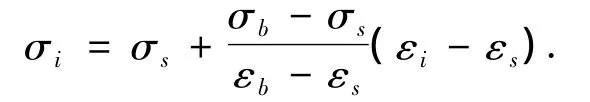
式中:σs、σb分别为材料的屈服强度和抗拉强度;εs、εb分别为屈服强度和抗拉强度所对应的应变．简化后

式中:σ0为初始屈服应力;K为材料强度系数．全量理论下，应力 -应变关系式为

通过式(4)及基本假设条件可以得到简化后等效应力和等效应变的表达式为

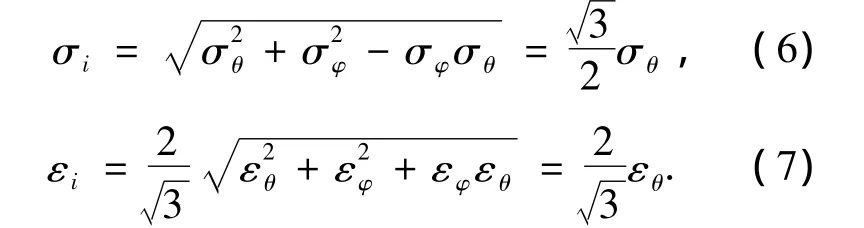
通过式(3)、(6)和(7)可以得到

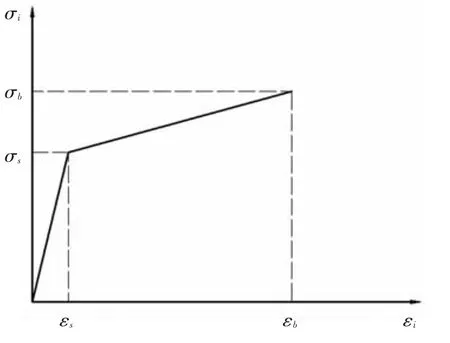
图4 弹塑性线性强化模型

将式(1)和式(8)带入式(2)，可以得出弯矩M的表达式为

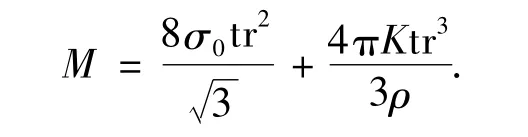
弯曲卸载后回弹的示意图如图5所示，中性层长度不变的条件下，有ρα =ρ0α0．卸载前的总应变ε、卸载后弹性应变εe和塑性应变εp分别为

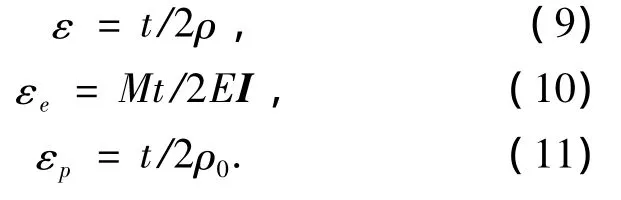
回弹后的曲率半径．

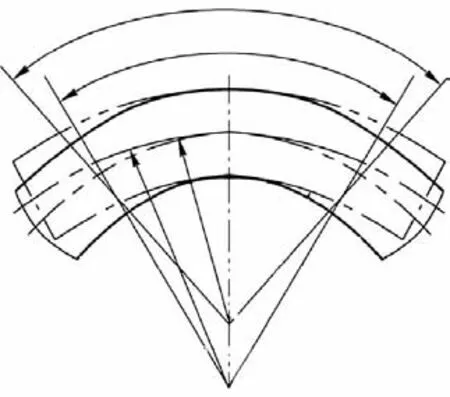
图5 弯曲回弹

根据式(9)～(11)可以得出回弹前后中性层曲率半径关系表达式为

回弹角Δα表达式为

3 回弹实验及线性回归关系

对于不同的材料，管材数控弯曲的回弹角与管材的弯曲角，芯轴与管壁的间隙以及材料的本构模型有关.对于同一种材料相同条件下，弯曲角是影响回弹的主要因素.管材数控弯曲实验在哈尔滨工业大学锻压车间CNC数控弯管机上进行.为了探索回弹量与弯曲角度的关系，进行了17组不同弯曲量的弯曲实验，弯曲角度范围为30°～70°，弯曲后如图6所示，通过测量不同弯曲角度及卸载后回弹角度如表1所示.

图6 不同弯曲角弯曲后管材

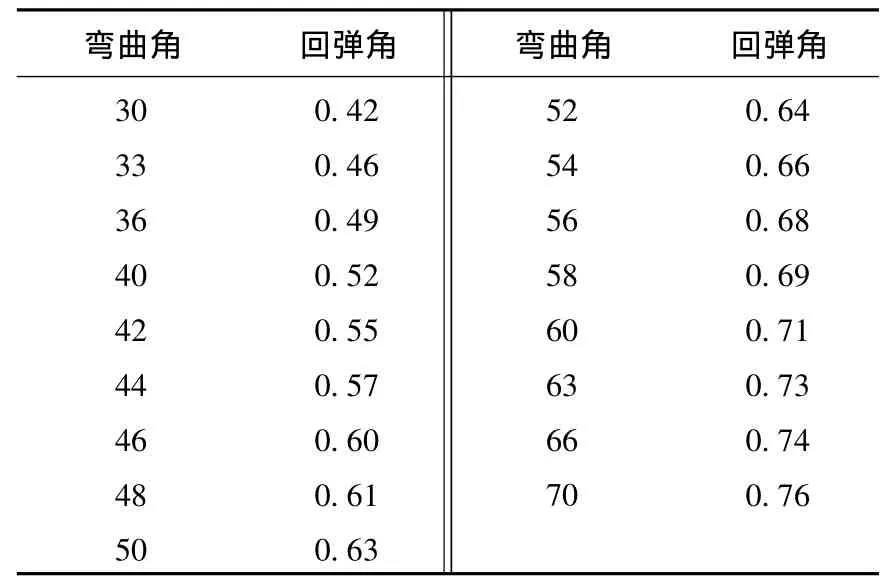
表1 弯曲前后角度对比 (°)

对上述数据进行线性拟合，得出回弹角与弯曲角的关系式为

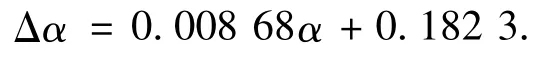
已知材料的屈服强度σs=320 MPa，抗拉强度σb=392 MPa，均匀延伸率δ=30%，弹性模量E=196 GPa，从而得出:K=242.3 MPa，σ0=319.5 MPa.管材的外径为 r=75.6 mm，t=2.8 mm，数控弯曲过程中性层曲率半径 ρ=153 mm，主要弯曲角度如图2所示.

通过以上数据，可以得出任意弯曲角下的回弹角理论计算值与实验的线性拟合值.具体对比情况如表2所示，实验得到回弹角与弯曲角的线性拟合关系与理论预测值相差很小，从而可以证明，该理论模型和材料模型在该范围内对任意弯曲角的回弹值的预测是合理的.

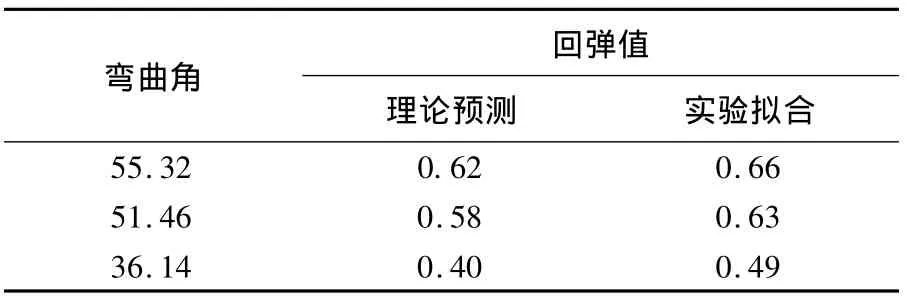
表2 理论预测值与实验线性拟合值对比分析 (°)

4 副车架内高压成形实验研究

按照图2所示的尺寸要求对管材进行数控弯曲，预成形和内高压成形，在合模后即产生如图7所示的起皱缺陷.该缺陷的产生来源于管材弯曲卸载后的回弹.

图7 副车架合模过程缺陷

为了避免因回弹而引起的缺陷，需要在弯曲过程进行回弹量的补偿.根据理论预测回弹值，对引起缺陷的弯曲角进行回弹补偿.分别将弯曲角55.32°和 51.46°修正为 55.94°和 52.04°，得到的管材在合模过程没有起皱缺陷，并顺利进行了内高压成形.

图8所示为弯曲角修改后的合模件，该试件完全消除起皱缺陷.图9所示为整形压力90 MPa并经过液压冲孔的合格副车架试件.试件整形效果良好，尺度精度较高.

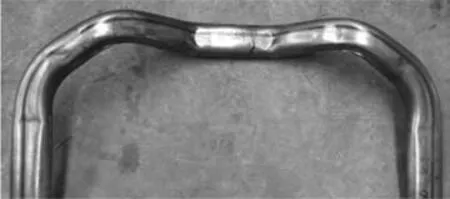
图8 弯曲角修正后的合模件

图9 内高压成形件

5 结论

1)通过建立管材塑性弯曲理论模型以及材料的弹塑性线性强化模型，得到回弹角与弯曲角变化的解析式，该方法得到实验的验证.

2)由于弯曲回弹的存在，使副车架合模过程产生起皱缺陷.通过理论计算得到的回弹角与弯曲角的关系，对数控弯曲角度进行回弹补偿，从而消除了起皱缺陷，得到合格的内高压成形件.

［1］MAKI T.Sheet hydroforming of automotive body panels in automotive structures［C］//International Conference on Hydroforming.Fellbach，Germany，2005:187-202.

［2］YUAN Shijian，HE Zhubin，LIU Gang.New developments of hydroforming in China［C］//Proceedings of the 5th International Conference on Tube Hydroforming.Kenichi Manabe，Japan:SPARC，2011:2-13.

［3］MIHARA Y.Development of tube hydroforming technology and research on formability of tube in Japan［C］//Proceedings of the 5th International Conference on Tube Hydroforming.Ken-ichiManabe， Japan:SPARC，2011:26-36.

［4］YUAN Shijian，HAN Cong，WANG X S.Hydroforming of automotive structural components with rectangularsections［J］.International Journal of Machine Tools and Manufacture，2006，46(11):1201-1206.

［5］王仲仁，张琦.省力与近均匀成形——原理与应用［M］.北京:高等教育出版社，2010.

［6］苑世剑，何祝斌，刘钢，等.内高压成形理论与技术新进展［J］.中国有色金属学报，2011，21(10):2523-2533.

［7］宋飞飞，杨合，李恒，等.TA18高强钛管数控弯曲回弹工艺参数影响的显著性分析［J］.稀有金属材料与工程，2013，42(1):43-48.

［8］詹梅，杨合，栗振斌.管材数控弯曲回弹规律的有限元分析［J］.材料科学与工艺，2004，12(4):349-352.

［9］QURESHI A，RUSSO A.Spring-back and residual stresses in bending ofthin-walled aluminium tubes［J］.Materials and Design，2002，23(2):217-222.

［10］MURATA M，KUBOKI T，TAKAHASHI K，et al.Effect of hardening exponent on tube bending［J］.Journal of Materials Processing Technology，2008，201(1/3):189-192.

［11］余同希.塑性弯曲理论及应用［M］.北京:科学出版社，1992.