具有未知死区的SⅠSO非仿射非线性系统间接自适应模糊控制

周卫东，廖成毅，郑 兰，程 华

(1.哈尔滨工程大学自动化学院，150001哈尔滨;2.齐齐哈尔市建华机械有限公司，161006黑龙江 齐齐哈尔)

在工业过程中经常遇到死区现象，其非线性特性会严重影响控制系统的性能，甚至可能导致系统不稳定.因此，许多学者对具有未知死区非线性输入的系统作了大量研究，并取得了一定的成果［1-13］.文献［1-2］针对一类具有死区环节的非线性系统提出构造死区反函数来补偿死区环节对系统带来的影响，但是该方法中不光滑的反函数可能会导致系统发生抖振现象.Zhou J.等通过设计光滑的死区反函数避免了抖振问题［3-4］.文献［5-6］分别针对运动控制系统和直流电机系统提出了模糊设计方法，即根据专家经验设计基于模糊逻辑系统的死区补偿器，利用模糊方法构造控制器，然而该方案会过度地依赖于专家经验，当找不到合适的描述死区非线性特性的模糊规则时，不能利用这种方法处理死区问题.在文献［7-9，11-13］中，死区被分解为一个线性项和一个有界的扰动类似项，然后利用鲁棒控制技术设计控制器，取得了理想的控制效果.上述研究均是针对仿射非线性系统，而大多数实际系统如飞控系统、化学反应控制系统等都是非仿射系统，近年来非仿射非线性系统的研究取得了很多成果［14-17］，遗憾的是针对非仿射非线性系统的研究，几乎没有人考虑含有死区输入的情况.

本文针对一类具有未知死区输入环节的SISO非仿射非线性系统，给出了一种间接自适应模糊控制方法.当系统状态可测时，采用模糊逻辑系统逼近系统中的非线性函数，构造了间接自适应模糊控制器.当系统状态不可测时，设计观测器估计跟踪误差，基于估计得到的状态设计间接自适应模糊输出反馈控制器.最后利用Lyapunov稳定性定理证明了跟踪误差收敛到零的某一邻域，同时保证闭环系统所有信号有界.

1 问题描述

考虑如下一类SISO非仿射系统

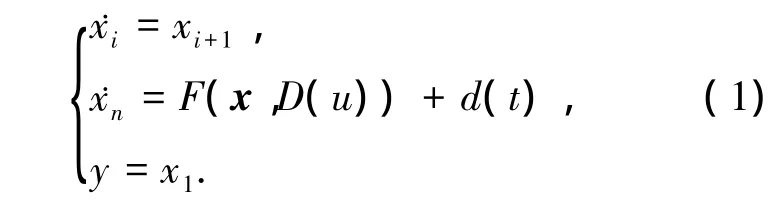
其中:u∈R为系统输入量，y∈R为系统输出量，x=［x1，…，xn］T∈Rn为系统的状态向量，d(t)为外界干扰且存在常数 d 满足 |d(t)|≤ d，F(x，D(u))为光滑的未知函数，D(u)为参数未知的死区输入．

控制目的:设计控制器使得系统输出y跟踪指定期望轨迹yd，同时闭环系统所有信号均有界．

假设1 对于任意x∈Ωx⊂Rn，存在大于零的常数g使得函数，满足条件g＜g(x)≤成立，其中Ωx为系统的可控域．

假设2 yd(t)及其对时间导数y(i)d(t)为有界的光滑函数，i=1，2，…，n．

假设3 对于任意x∈Ωx⊂Rn存在常数gr使得|·g(x)|≤gr成立．

输入为u输出为D(u)的死区模型描为

死区模型满足条件:1)死区输出D(u)不可测;2)死区参数未知，满足0≤br≤br，0≤bl≤bl，0＜ml≤ml，0＜mr≤mr．

将未知死区转化为

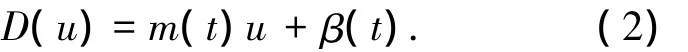
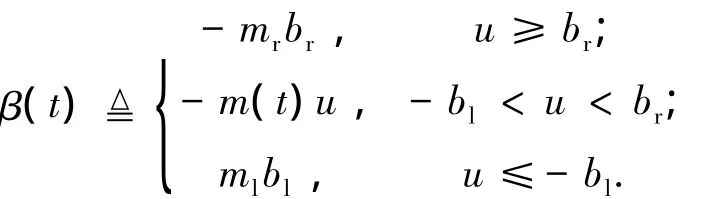
2 自适应模糊控制器设计

首先利用中值定理将非仿射非线性形式转化为仿射非线性形式，有

其中:f(x)=F(x，0)，λ ∈［0，D(u)］，

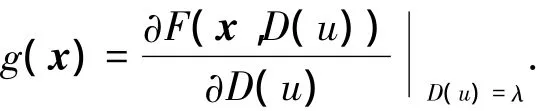
结合式(2)，系统(1)可转换为

其中:d0=g(x)β(t)+d(t)，则存在大于零的常数0使得 |d0|≤0．

针对经转化得到的仿射非线性系统，分系统状态可测与不可测两种情况进行分析.

2.1 系统状态可测

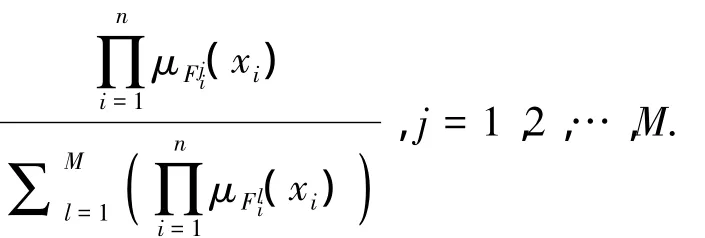
根据模糊逻辑系统的万能逼近特性［18］，存在最优逼近参数分别满足

估计误差为

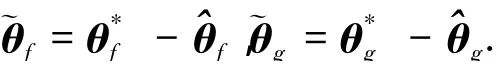
定义最优逼近误差为

定义跟踪误差e=yd-y，则误差向量e=［e，，…，e(n-1)］T．

由式(3)有系统跟踪误差方程为

式中:B=［0…01］T，

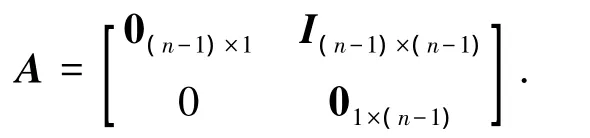
选择向量 K= ［kn，kn-1，…，k1］T使得 sn+k1sn-1+k2sn-2+kn为Hurwitz多项式．因此A1=A-BKT为稳定的矩阵，即给定一个正定对称矩阵P，存在正定矩阵Q满足Lyapunov方程

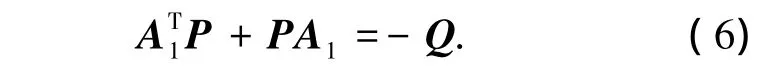
定理1 对于系统(1)，采用如下控制律与自适应律，可以使得系统输出跟踪给定期望信号，同时保证闭环系统所有信号均有界.

控制律为

自适应律为

其三，巡检工作不到位。在城市燃气管道投入运行之后，城市燃气管道相关单位承担着管道运行维护的责任，它们需要组织人员对管道日常运行进行巡检，及时发现并排除一些潜在的安全隐患或是突发问题，这样可以最大程度的避免燃气泄露事故的发生。然而在实际工作中，管道运行巡检工作不到位的情况十分常见，这也为燃气泄露埋下了隐患。

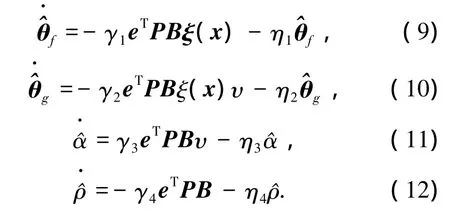
证明 取如下Lyapunov候选函数

对V求时间的导数并结合(5)、(6)可得

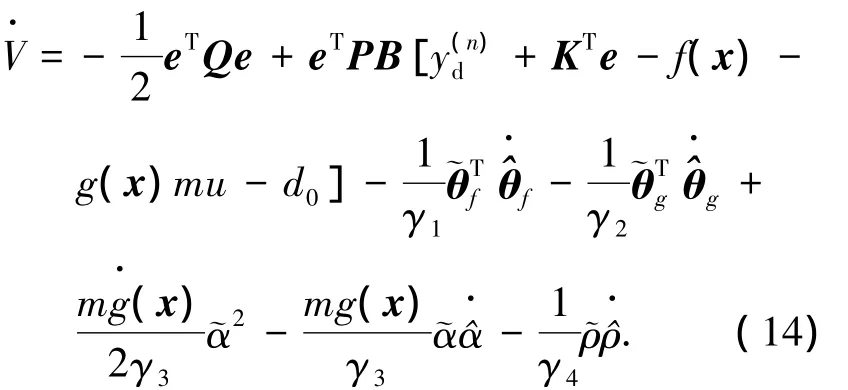
将控制律式(7)、(8)以及自适应律式(9)～(12)代入式(14)整理可得

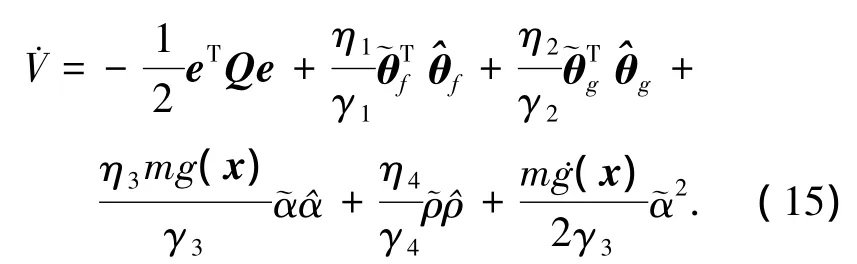
根据假设1和假设3，利用不等式性质整理式(15)有

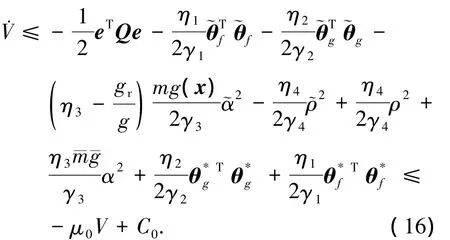
其中:μ0=，选取 η3使得 η3-＞0．

由式(16)可得

2.2 系统状态不可测

在实际工程中，通常只有系统输出可测，而系统状态通常是不可测量的，即y可测，=［x2，…，xn］T不可测．此时只能利用状态的估计=［1，…，n］T设计间接自适应模糊控制器．

跟踪误差向量为e=［e，，…，e(n-1)］T，定义

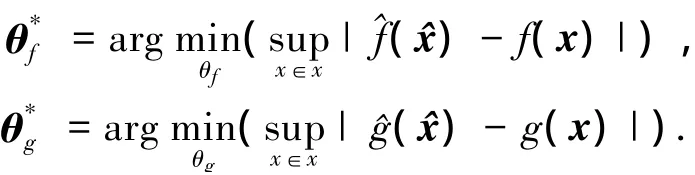
参数误差为

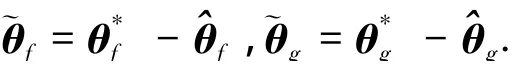
定义f(x)和g(x)的最优逼近误差为

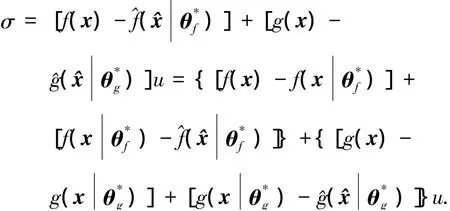
由式(4)可得系统跟踪误差方程为

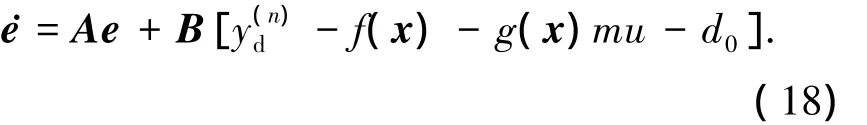
设计误差观测器为

式中:C=［1，0，…，0］T为反馈增益为观测器增益，选择K0、Kc分别使A-、A-KcCT为稳定矩阵．

假设4 正定矩阵P1和P2分别满足方程

由式(18)、(19)可得

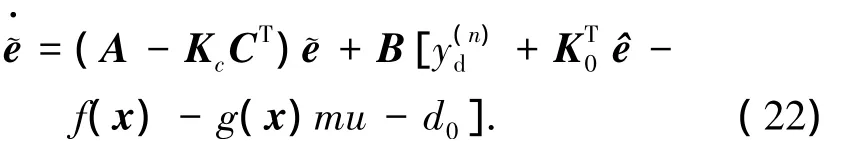
定理2 对于系统(1)，当系统状态不可测时，采用如下控制律和自适应律，可以使得系统输出跟踪给定期望信号，同时保证闭环系统所有信号均有界.

控制律

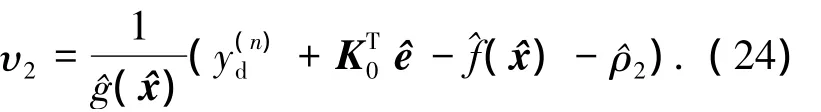
自适应律

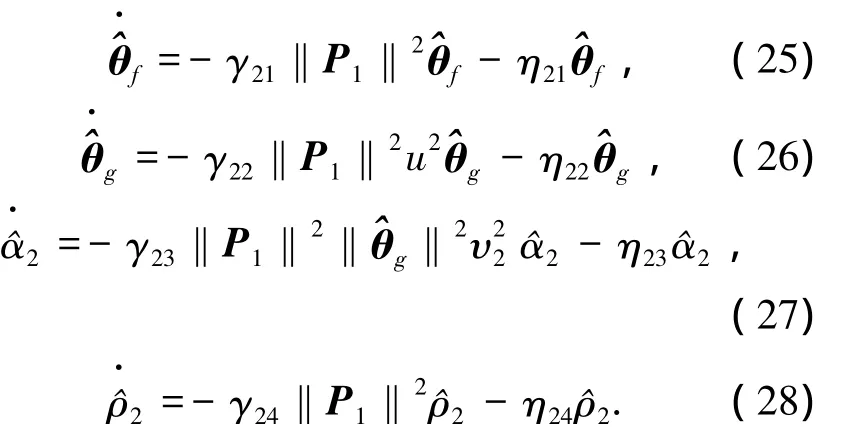
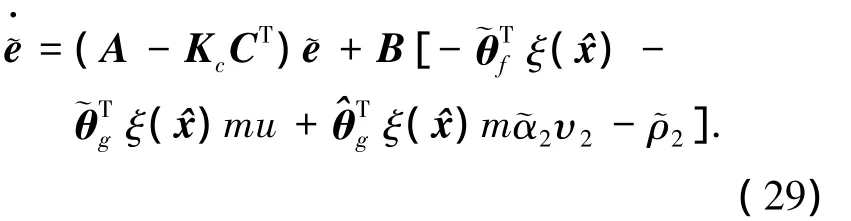
构造如下Lyapunov候选函数

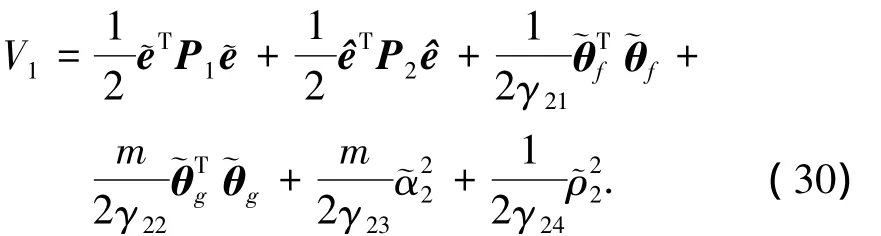
求V1关于时间的导数

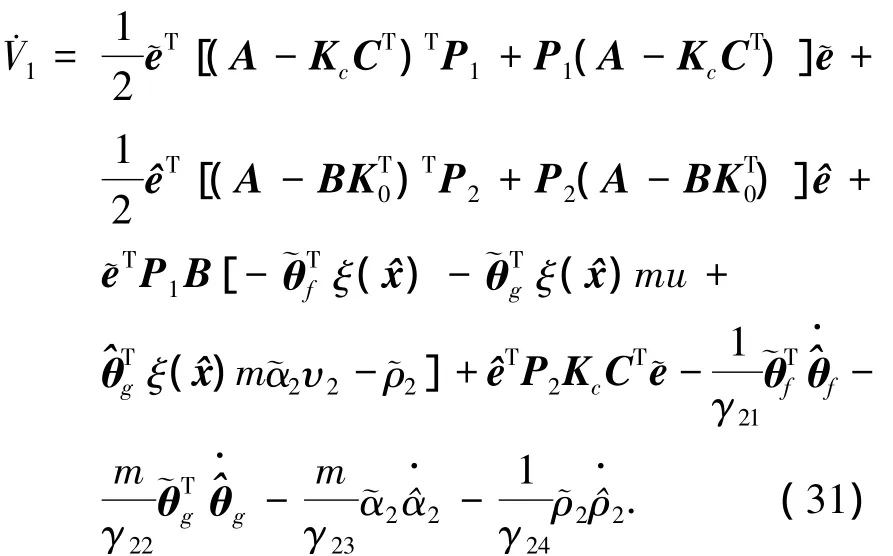
将式(20)、(21)代入式(31)有

整理可得

假设存在常数 M、N、ϑ分别满足不等式|u|≤M，|υ|≤N，‖θg‖2≤ϑ．将自适应律式(25)～(28)代入式(32)整理有

对式(33)两端求积分有

3 仿真结果

考虑如下非仿射非线性系统

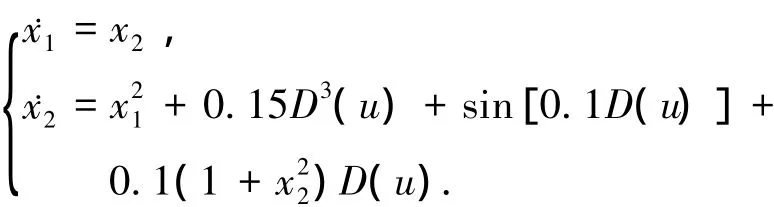
仿真目的是验证所设计控制器能使系统的输出y跟踪期望轨迹yd=sin(t)．仿真实验将分系统状态可测与不可测两种情况进行．其中死区D(u)定义为

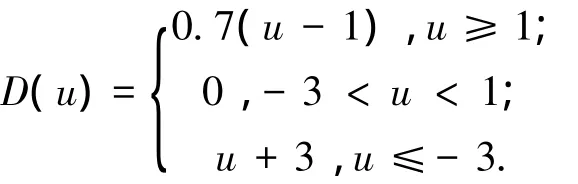
模糊隶属度函数选取分别为

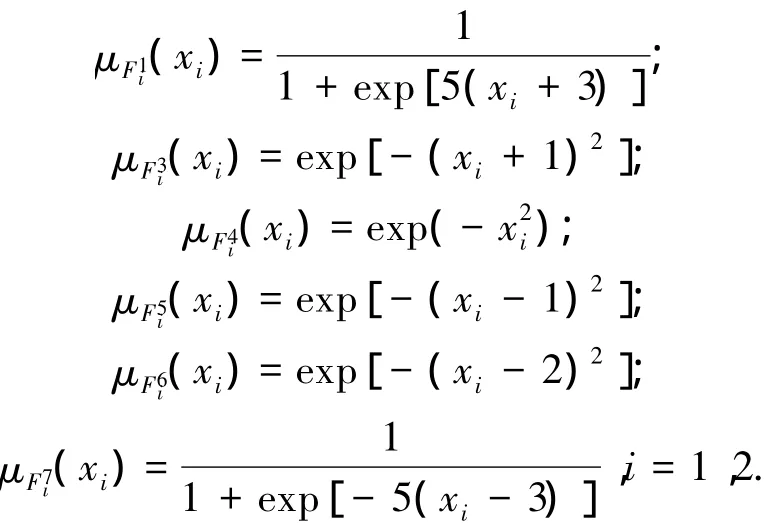
状态可测时，参数取值:γ1=0.01、γ2=0.01、γ3=0.01、γ4=0.01、η1=0.08、η2=0.08、η3=0.08、η4=0.08、K=［2510］T、P=．仿真过程中初值设定(0)=0.1(0)= ［0.1…0.1］1×49、x1(0)=1、=［0.1…0.1］1×49、x2(0)=0．仿真时间为30 s，仿真结果如图1～3所示．

状态不可测时，参数取值:γ21=0.01、γ22=0.01、γ23=0.01、γ24=0.01、η21=0.001、η22=0.001、η23=0.001、η24=0.001、K0=［104］T、Kc=［45］T、P1=．仿真初值设定:［0.1…0.1］1×49(0)=［10］T．仿真时间取为30 s，结果如图4～6所示.

由图1和图4可以观察到系统输出跟踪期望信号的轨迹，结合跟踪误差图2和图5，可以得出结论，利用本文所设计的控制器，可以使得系统完成跟踪任务，即跟踪误差收敛于零的某一邻域.图3和图6则分别给出了两种情况下系统控制输入的轨迹曲线.经上述分析，本文给出的控制器能够使得系统输出跟踪给定轨迹，并同时保证了跟踪误差收敛以及控制输入有界.

图1 状态可测时期望输出与实际跟踪曲线

图2 状态可测时跟踪误差曲线

图3 状态可测时系统控制输入曲线

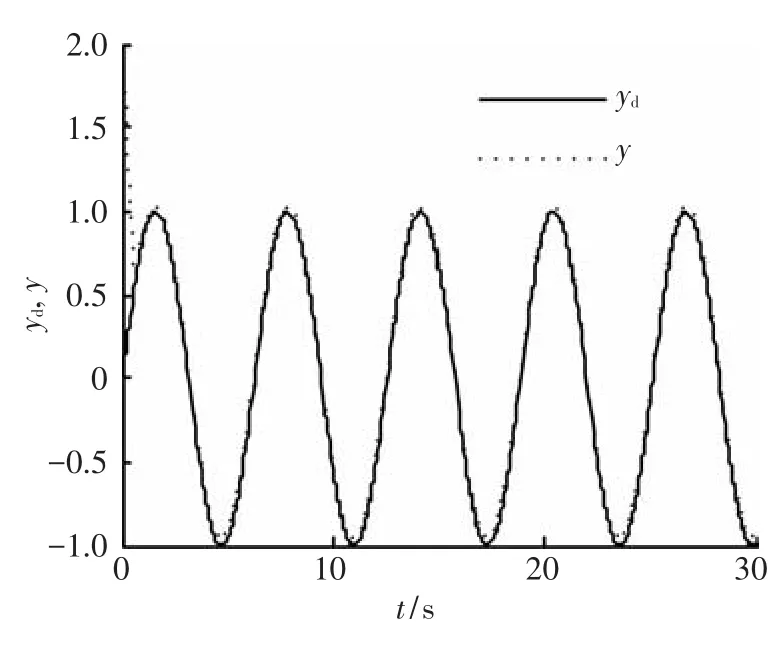
图4 状态不可测时期望输出与实际跟踪曲线

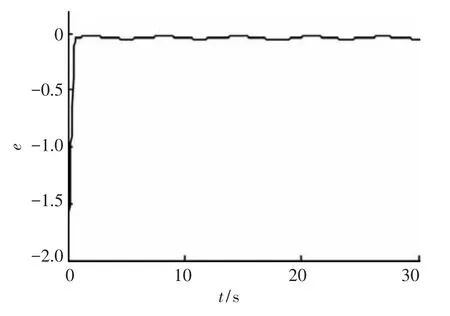
图5 状态不可测时跟踪误差曲线

图6 状态不可测时系统控制输入曲线

5 结 论

1)研究了一类含有未知死区输入环节的SISO非仿射非线性系统控制器设计问题，给出了在系统状态可测与不可测两种情况下的控制器设计方案.

2)通过Lyapunov定理证明了具有未知死区的SISO非仿射非线性闭环系统的稳定性，跟踪误差收敛，同时保证了所有系统均有界.

［1］CHO H，BAI E.Convergence results for an adaptive dead zone inverse ［J］.Int J Adapt Control Signal Processing，1998，12(5):451-466.

［2］TAWARE A，TAO Gang，TEOLIS C.Design and analysis of a hybrid control scheme for sandwich nonsmooth nonlinear systems［J］.IEEE Trans Autom Control，2002，47(1):145-150.

［3］ZHOU Jing，WEN Changyun，ZHANG Ying.Adaptive output control of nonlinear systems with uncertain deadzone nonlinearity ［J］.IEEE Trans Autom Control，2006，51(3):504-511.

［4］ZHOU Jing，SHEN X Z.Robust adaptive control of nonlinear uncertain plants with unknown dead-zone［J］.IET Control Theory Appl，2007，1(1):25-32.

［5］LEWIS F L，TIM W K，WANG L Z，et al.Dead-zone compensation in motion control systems using adaptive fuzzy logic control［J］.IEEE Trans Contr Syst Technol，1999，7(6):731-742.

［6］JANG J O.A dead-zone compensator of a DC motor system using fuzzy logic control［J］.IEEE Trans Man，Systems and Cybernetics:Applications and Reviews，2001，31(1):42-48.

［7］WANG Xingsong，SU Chunyi，HONG H.Robust adaptive control of a class of linear systems with unknown dead-zone ［J］.Automatica，2004，40(3):407-413.

［8］张天平，裔扬，梅建东.带有未知死区模型的鲁棒自适应模糊控制［J］.控制与决策，2006，21(4):367-370.

［9］IBRIR S，XIE Wenfang，SU Chunyi.Adaptive tracking of nonlinear systems with non-symmetric dead-zone input［J］.Automatica，2007，43(3):522-530.

［10］沈启坤，张天平.具有未知非线性死区的自适应模糊控制［J］.控制与决策，2007，22(6):689-692.

［11］HUA Changchun，WANG Qingguo，GUAN Xinping.Adaptive tracking controller design of nonlinear systems with time-delays and unknown dead-zone input［J］.IEEE Trans Autom Control，2008，53(7):1753-1759.

［12］ADLOO H，NOROOZI N，KARIMAGHA P.Observer based model reference adaptive control for unknown time-delay chaotic systems with input nonlinearity ［J］.Nonlinear Dynamic，2012，67:1337-1356.

［13］TONG Shaocheng，LI Yongming.Adaptive fuzzy output feedback control of MIMO nonlinear systems with unknown dead-zone inputs［J］.IEEE Trans Fuzzy Syst，2013，21(1):134-146.

［14］LABIOD S，GUERRA T M.Adaptive fuzzy control of a class of SISO nonaffine nonlinear systems［J］.Fuzzy Sets Syst，2007，158(10):1126-1137.

［15］WEN Jie，JIANG Changsheng.Adaptive fuzzy controller for a class of strict-feedback nonaffine nonlinear systems［J］.Journal of Systems Engineering and Electronics，2011，22(6):967-974.

［16］MAO Zhizhong，XIAO Xiaoshi.Decentralized adaptive tracking control of nonaffine nonlinear large-scale systems with time-delays ［J］.Inf Sci，2011，181(23):5291-5303.

［17］BOULKROUNE A，MSAAD M，FARZA M.Adaptive fuzzy tracking control for a class of MIMO nonaffine uncertain systems ［J］.Neurocomputing，2012，93:48-55.

［18］WANG Lixin.A course in fuzzy systems and control［M］.Englewood Cliffs，NJ:Prentice Hall，1997.