CRTSⅡ型板式轨道关键参数对高速车辆－轨道垂向耦合振动响应的影响①

徐浩，张梦楠，赵坪锐，王平

(西南交通大学高速铁路线路工程教育部重点实验室，四川成都 610031)

CRTSⅡ型板式无砟轨道是在德国博格板式无砟轨道系统基础上研发的新型轨道结构，目前已经在京津城际高速铁路和京沪高速铁路上广泛应用，但是其铺设范围以桥梁、隧道区段居多，土质路基区段应用较少。路基上CRTSⅡ型板式无砟轨道由钢轨、扣件系统、预制轨道板、水泥乳化沥青砂浆(CA砂浆)层和混凝土支承层等组成，为了推广CRTSⅡ型板式无砟轨道在土质路基上的应用，需要系统研究轨道结构关键参数对行车安全性的影响。目前，许多学者开展了板式无砟轨道动力学的研究。徐鹏等［1］研究了土质路基上纵连板式无砟轨道的动力性能，结果表明水泥乳化沥青砂浆(CA砂浆)的最大动应力为46.8～50.5 kPa，远小于砂浆层的设计指标值15 MPa，纵连板式无砟轨道及路基的动变形随深度衰减较慢，动应力随深度衰减较快。王平等［2］分析了轨道板开裂对路基上CRTSⅡ型板式无砟轨道动力力特性的影响，轨道板开裂将增大轨道板的振动响应。向俊等［3－5］研究了车速、轨道几何不平顺、CA砂浆刚度及阻尼等参数对轨道动力特性的影响，认为合理的CA砂浆刚度取值范围为1.0 ～1.5 GPa。徐浩等［6］针对单元板式无砟轨道，研究扣件刚度突变对行车安全性的影响，建议及时对扣件系统进行养护检修，保证行车的平稳性和安全性，拟将路基上CRTSⅡ型板式无砟轨道和高速列车作为研究对象，利用轮轨系统耦合动力学理论，研究CRTSⅡ型板式无砟轨道关键参数变化对高速列车的振动特性和轮轨相互作用力的影响，为CRTSⅡ型板式无砟轨道结构的进一步优化提供理论指导。

1 计算模型及求解方法

本文仅考虑车辆、轨道、路基的垂向振动，根据轮轨系统耦合动力学理论和有限元方法［7－8］，建立列车－轨道－路基系统垂向耦合振动计算模型，如图1所示。轨道模拟为考虑钢轨、轨道板和混凝土支承层参振的3层点支承梁模型。钢轨采用欧拉梁模拟，扣件系统采用线性弹簧阻尼单元模拟，轨道板和混凝土支承层之间的水泥乳化沥青砂浆层简化为连接二者的弹簧和阻尼单元，路基简化为均布的线性弹簧和阻尼单元。

图1 列车－轨道－路基垂向耦合振动平面模型Fig.1 Vehicle－track－subgrade vertical coupling vibration plane model

车辆视为一个由悬挂弹簧和阻尼联系起来的7个刚体(1个车体、2个构架、4个轮对)振动系统，其中车体和构架具有沉浮和点头2个自由度，而轮对仅考虑沉浮自由度，一节车辆共10个自由度。轮轨之间的法向作用力由赫兹非线性弹性接触理论确定。

根据显示动力学理论，运用大型通用显式动力分析程序LS－DYNA的显示中心差分法求解动力学响应方程，具体的求解方法在文献［2，6，9］有详细说明。

2 计算参数及模型验证

模型中钢轨采用CHN60轨，扣件节点刚度取50 kN/mm，扣件阻尼为60 kN·s/m，扣件间距为650 mm;由于CRTSⅡ型板式无砟轨道的轨道板之间通过两端的6根直径为20 mm连接钢筋相互连接，保证了轨道板纵向连续性，因此计算模型中轨道板采用连续模型，且模拟轨道板的梁长度与模型总长度相等，抗弯刚度按宽度1.275 m(取半宽)、厚0.2 m、混凝土强度C55计算;模拟水泥乳化沥青砂浆层的线性弹簧根据其弹性模量7 000 MPa换算得到，砂浆的阻尼取为50 kN·s/m3。模拟水泥乳化沥青砂浆层的线性弹簧刚度可根据如下公式计算得到:

式中:KCA为CA砂浆层的面刚度;ECA为CA砂浆的弹性模量;hCA为CA砂浆层的厚度。

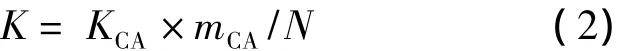
式中:K为模拟CA砂浆层的线性弹簧的刚度;mCA为水泥乳化沥青砂浆层的面积;N为模拟水泥乳化沥青砂浆层的线性弹簧总数。

模拟支承层的梁长度与模型总长相等，抗弯刚度按宽度 1.625 m(取半宽)、厚 0.3 m、弹性模量7 000 MPa计算。路基基础的支承刚度按75 MPa/m计算［10］，列车采用CRH2型动车组的1节动车模拟，以300 km/h的速度通过路基地段。动车轮重为70 kN，根据赫兹接触理论计算得动车和拖车的轮轨间等效接触刚度分别为1.193 GN/m。

轨道不平顺采用德国低干扰谱，图2为根据陈果等［11］提供的方法计算得到的时域随机不平顺样本(x为距离模型左端的距离)。模型在钢轨两端进行全约束，模拟路基弹簧的底部全约束，车辆运行时计算起点和两端是同步的。

图2 德国低干扰谱时域随机不平顺样本Fig.2 Time domain random irregularity sample of the Germanic low－disturbance spectrum

为验证本文所建立的列车－轨道－路基垂向耦合振动模型的正确性，采用如上计算参数进行动力响应分析，轮轨垂向相互作用力时程曲线如图3所示;图4为模型中部钢轨垂向位移时程曲线。

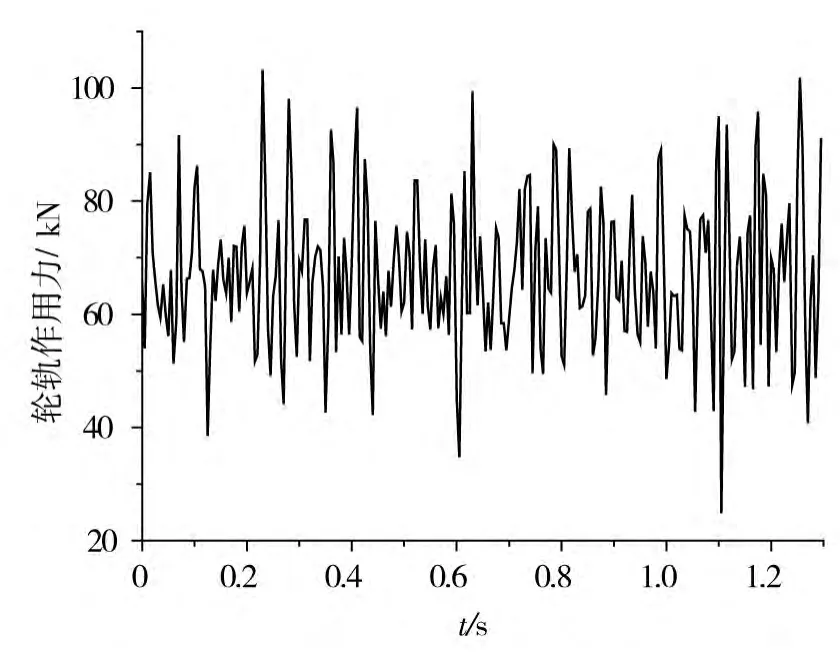
图3 轮轨垂向力时程曲线Fig.3 Time history of vertical wheel－ rail forces

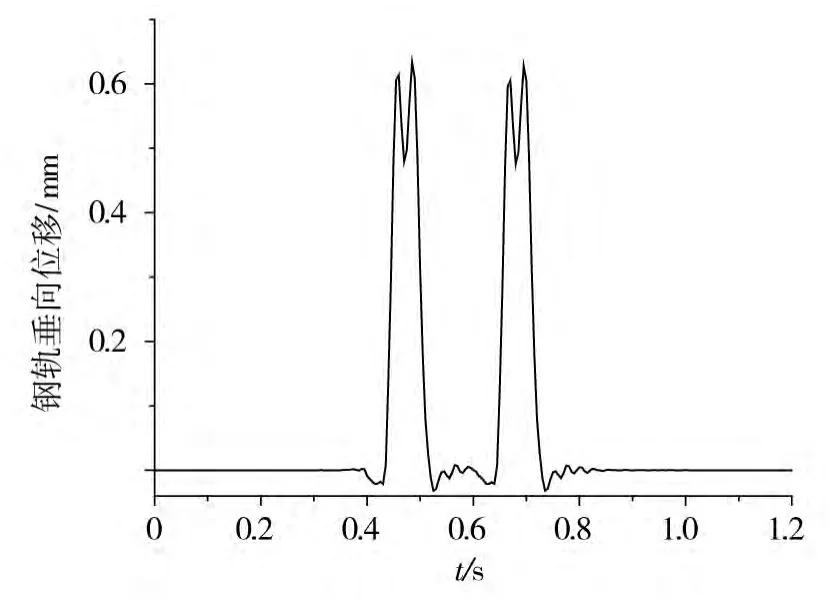
图4 钢轨垂向位移时程曲线Fig.4 Time history of vertical displacement of rail

表1给出了动力响应各指标仿真计算结果最大值与文献［1］以及京津城际铁路实测结果［12］的对比值，从表1可知，仿真结果与各文献及实测结果具有较好的一致性，验证了计算模型的可靠性。

表1 仿真计算结果与文献及实测结果对比Table 1 Comparison of measured data and calculated results

3 结果与分析

利用所建立的模型，通过修改相关参数分析CRTSⅡ型板式无砟轨道结构关键参数对行车安全性的影响，主要考虑轨道板厚度、扣件系统刚度及阻尼、CA砂浆弹性模量及阻尼、混凝土支承层厚度等关键参数的影响。

3.1 轨道板厚度的影响

固定其他计算参数，只改变轨道板的厚度，轮轨相互作用力与高速列车的后转向架、后转向架后轮对、车体振动加速度最大值随轨道板厚度的变化趋势分别如图5和图6所示。

由图5及图6可知，随着轨道板厚度的增加，轮轨垂向相互作用力随之增加，但是车体、转向架以及轮对的振动加速度随之减小。当轨道板厚度从0.1 m增大到0.3 m时，轮轨垂向相互作用力增大0.53%，轮对、转向架的振动加速度分别减小了2.54%和3.25%，而车体的振动加速度变化较小，其幅度(0.15%)和量值(0.000 4g)均较小，由此可见轨道板厚度增加对行车平稳性基本无影响，但轮轨作用力增大将加剧轨下基础的破坏。

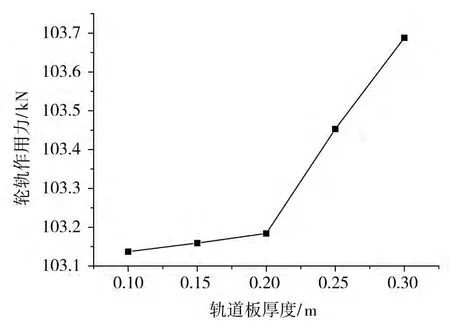
图5 最大轮轨作用力与轨道板厚度的关系Fig.5 Maximum wheel－ rail vertical force as a function of slab

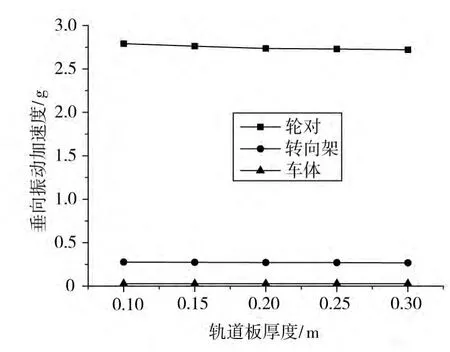
图6 车辆的最大垂向振动加速度与轨道板厚度的关系Fig.6 Vehicle－track－subgrade vertical coupling vibration plane model

3.2 扣件系统刚度及阻尼的影响

固定其他计算参数，只变化扣件系统的刚度或者阻尼，最大轮轨相互作用力与高速列车的后转向架、后转向架后轮对、车体的垂向振动加速度最大值随扣件系统刚度或阻尼的变化如表2所示。

从表2可知，随着扣件刚度的增大，最大轮轨垂向相互作用力和轮对、转向架的垂向振动加速度随之增大，而车体的垂向振动加速度变化较小。当扣件刚度从20 kN/mm增加到100 kN/mm时，最大轮轨垂向力增加29.83%，轮对和转向架的垂向振动加速度分别增大43.94%和7.98%，而车体的振动加速度则基本无变化，说明扣件刚度变化对行车平稳性基本无影响，降低扣件刚度能减小轮轨作用力，但过低的刚度将加剧轨道变形，因此在满足轨道几何形位和轨道动位移的基础上，应采用较低刚度的扣件系统。当扣件阻尼从20 kN·s/m增大到100 kN·s/m时，最大轮轨垂向相互作用力、轮对和转向架的垂向振动加速度分别减小了9.48%，21.64%和7.09%，但对行车平稳性基本无影响。可见，尽量采用大阻尼的扣件将有利于保证车辆运行的安全性，减小无砟轨道的疲劳损伤，延长轨道结构的使用寿命。

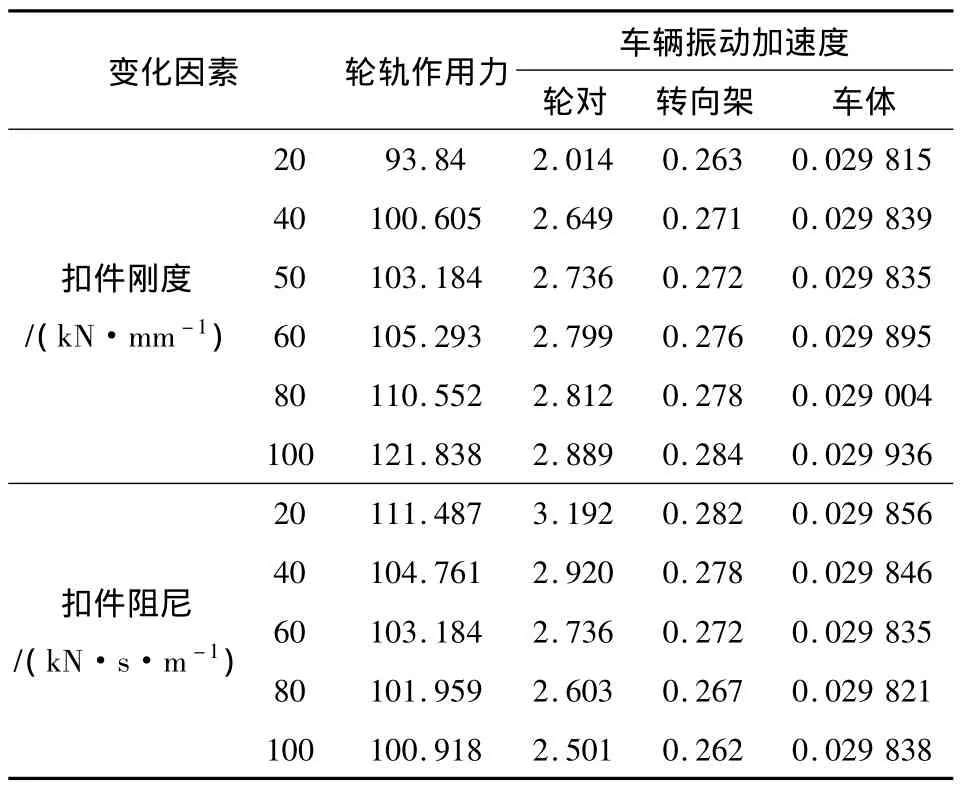
表2 不同扣件刚度或阻尼下最大轮轨垂向相互作用力和车辆的垂向振动加速度Table 2 Maximum wheel－rail vertical force and the vertical vibration acceleration of vehicle varying with fastener stiffness or damping

3.3 CA砂浆弹性模量及阻尼的影响

固定其他动力计算参数，只变化CA砂浆的弹性模量或阻尼，最大轮轨垂向相互作用力及轮对、转向架和车体的垂向振动加速度随CA砂浆弹性模量或阻尼的变化如表3所示。

从表3可知，CA砂浆的弹性模量或阻尼变化对最大轮轨垂向相互作用力及轮对、转向架和车体的垂向振动加速度基本上没有影响，这说明CA砂浆的弹性模量及阻尼对行车安全性和平稳性基本无影响。

3.4 混凝土支承层厚度的影响

固定其他动力计算参数，变化混凝土支承层的厚度，最大轮轨垂向相互作用力及轮对、转向架和车体的垂向振动加速度随混凝土支承层厚度的变化如图7和图8所示。

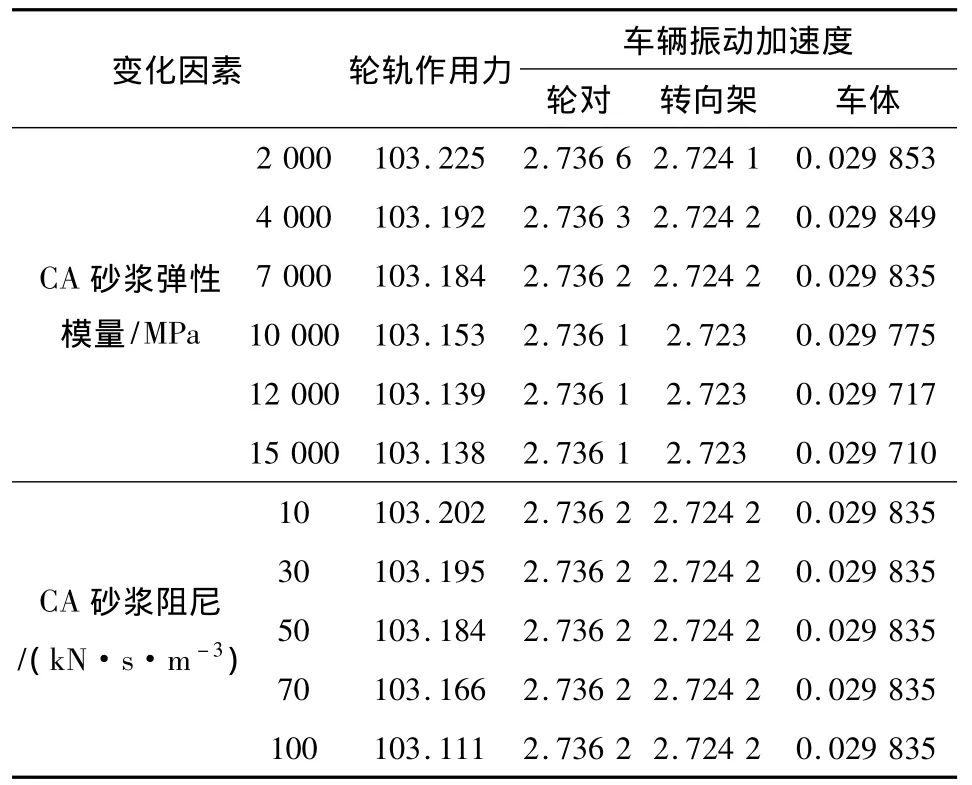
表3 不同CA砂浆弹性模量或阻尼下最大轮轨垂向相互作用力和车辆的垂向加速度Table 3 Maximum wheel－rail vertical force and the vertical vibration acceleration of vehicle varying with the elasticity modulus or damping of CA mortar

图7 最大轮轨垂向相互作用力与混凝土支承层厚度的关系Fig.7 Maximum wheel－ rail vertical force as a function of concrete supporting layer thickness

图8 车辆的最大垂向振动加速度与混凝土支承层厚度的关系Fig.8 Maximum vertical vibration acceleration of vehicle as a function of concrete supporting layer thickness

从图7和图8可知，随着混凝土支承层的厚度增加，最大轮轨垂向相互作用力及轮对、转向架和车体的垂向振动加速度均随之减小，这是由于混凝土支承层厚度的增大，增大了轨道结构的系统质量，从而降低系统的垂向振动加速度。当混凝土支承层厚度由0.1 m增大到0.5 m时，最大轮轨垂向相互作用力降低2.01%，轮对的垂向振动加速度减小了11.63%，在满足轨道结构高度的情况下，可适当增加混凝土支承层的厚度，以提高行车的平稳性。

4 结论

(1)轨道板厚度增加对行车平稳性基本无影响，但是会增大轮轨相互作用力，导致轨道结构的位移过大，对轨道结构受力不利，建议保证轨道板的厚度在一个合适的范围内。

(2)扣件刚度及阻尼变化对行车平稳性基本无影响;扣件刚度增大及扣件阻尼减小均会造成轮对和转向架的垂向加速度增大，可能会加速轮对及转向架的疲劳损伤等;因此在满足轨道几何形位和轨道动位移的基础上，应采用较低刚度的扣件系统，同时应尽可能增大扣件的阻尼，保证行车的安全性和平稳性。

(3)CA砂浆的弹性模量及阻尼对轮对作用力及车辆的振动特性基本无影响，建议CA砂浆的基本参数满足板式无砟轨道的力学及功能要求即可。

(4)随着混凝土支承层厚度增大，最大轮轨相互作用力及车辆振动均随之减小，但对行车平稳性基本无影响;建议在满足轨道结构高度要求的情况下，可适当增大混凝土支承层的厚度以保证高速行车的安全性和平稳性。

［1］徐 鹏，蔡成标.路基上纵连板式无砟轨道动力特性分析［J］.西南交通大学学报，2011，46(2):189 －194.XU Peng，CAI Chengbiao.Dynamic analysis of longitudinally connected ballastless track on earth subgrade［J］.Journal of Southwest Jiaotong University，2011，46(2):189－194.

［2］王平，徐浩，陈嵘，等.路基上CRTSⅡ型板式轨道裂纹影响分析［J］.西南交通大学学报，2012，47(6):929－934.WANG Ping，XU Hao，CHEN Rong，et al.Effects anal-ysis of cracking of CRTSⅡslab track on subgrade［J］.Journal of Southwest Jiaotong University，2012，47(6):929－934.

［3］向俊，曹晔，刘保钢，等.客运专线板式无碴轨道动力设计参数［J］.中南大学学报(自然科学版)，2007，38(5):981－986.XIANG Jun，CAO Ye，LIU Bao － gang，ed al.Dynamic parameters of slab Track of Passenger Transport Line［J］.Journal of Central South University(Natural Science Edition)，2007，38(5):981 －986.

［4］赫丹，向俊，曾庆元.轨道刚度变化对高速列车－板式轨道系统振动响应的影响分析［J］.西安建筑科技大学学报(自然科学版)，2006，38(4):559－563.HE Dan，XIANG Jun，ZENG Qingyuan.Analysis of Effect of Track Stiffness Change on Vibration Response of High－speed Train and Slab Track System［J］.Journal of Xi'an University of Architecture＆Technology(Natural Science Edition)，2006，38(4):559－563.

［5］赫丹，向俊，郭高杰，等.砂浆刚度和阻尼对高速列车－板式轨道时变系统竖向振动的影响［J］.铁道科学与工程学报，2006，3(3):26－30.HE Dan，XIANG Jun，GUO Gaojie，et al.The effect of stiffness and damping of cement asphalt mortar on the vertical of the high－speed train and slab track time－dependent system［J］.Journal of Railway Science and Engineering，2006，3(3):26－30.

［6］徐浩，李培刚，王平，等.单元板式轨道扣件刚度突变对行车安全性的影响分析［J］.中国安全科学学报，2012，22(3):134－139.XU Hao，LI Peigang，WANGPing，et al.Analysis of impact of mutation of unit slab track fastener stiffness on train running safety［J］.China Safety Science Journal，2012，22(3):134－139.

［7］ Wangming Zhai，Kaiyun Wang，Chengbiao Cai.Fundamentals of vehicle － track coupled dynamics［J］.Vehicle System Dynamics，2009，47(11):1349 －1376.

［8］Wangming ZHAI，Chengbiao CAI，Shizhang GUO.Copling model of vertical and lateral vehicle/track interactions［J］.Vehicle System Dynamics，1996，26(1):61 －79.

［9］李培刚，刘学毅，郝远行.涵洞地段道砟垫的减振特性［J］.西南交通大学学报，2012，47(2):192－197.LI Peigang，LIU Xueyi，HAO Yuanxing.Damping Characteristics of Ballast Mat on Culvert［J］.Journal of Southwest Jiaotong University，2012，47(2):192 －197.

［10］宋小林，翟婉明.高速移动荷载作用下CRTSⅡ型板式无砟轨道基础结构动应力分布规律［J］.中国铁道科学，2012，33(4):1 －7.SONG Xiaolin，ZHAI Wanming.Dynamic Stress Distribution of the Infrastructure of CRTSⅡSlab Ballastless Track under High Speed Moving Load［J］.China Railway Science，2012，33(4):1 －7.

［11］陈果，翟婉明.铁路轨道不平顺随机过程的数值模拟［J］.西南交通大学学报，1999，34(2):138 －142.CHEN Guo，ZHAI Wanming.Numerical simulation of random process about railway track irregularity ［J］.Journal of Southwest Jiaotong University，1999，34(2):138－142.

［12］张曙光.京津城际高速铁路系统调试技术［M］.北京:中国铁道出版社，2008.ZHANG Shuguang.Beijing－Tianjin intercity highspeed railway system debugging technique［M］.Beijing:China Railway Publishing House，2008.