基于磨料磨损的TBM滚刀磨损预测研究①

赵海鸣，舒标，夏毅敏，郑伟

(1.中南大学机电工程学院，湖南 长沙 410083;2.中南大学高性能复杂制造国家重点实验室，湖南长沙 410083)

随着隧道和地下空间技术的快速发展，隧道掘进机(TBM)在硬岩隧道掘进中扮演着越来越重要的作用。刀具在TBM工作过程中将岩石破碎，其切削性能直接影响TBM的工作效率。目前，盘形滚刀由于有着高效的切削性能，在硬岩隧道掘进机破岩时起着重要作用。在施工过程中，滚刀的工作条件极其恶劣，消耗量极大，频繁的换刀严重影响了施工进度。滚刀刀圈失效形式包括正常磨损、非正常磨损、卷边、打刃、移位和崩裂等损坏形式，正常磨损为滚刀刀圈损坏的主要形式［1－2］。在滚刀的磨损以及磨损预测方面的研究，科罗拉多矿业学院模型(CSM)［3］根据不同岩石对滚刀刀圈的不同磨损程度提出磨蚀性指数(CAI)来预测滚刀寿命。挪威科技大学模型(NTU)［4］提出滚刀寿命指数(CLI)，即用一个特定的磨耗值(AV)来预测滚刀寿命。王礼惠等［5］运用比能法，根据实际施工数据的变化来预测滚刀刀圈半径的减少量。张照煌［6］提出弧长磨损量的概念，根据滚刀刀圈上每点切削岩石所走过的弧长长度预测磨损量。李笑等［7］利用滚刀在前一段时间的实际磨损数据，建立一种基于多元非线性回归预测模型来对滚刀磨损量进行预测。上述的滚刀磨损预测模型集中关注于滚刀切削岩石的力学特性、工程实际数据、岩石特性，并以此为依据来评判滚刀的磨损性能，较少考虑滚刀自身的性能;部分研究虽然指出了滚刀的磨损形式，但较少对磨损机制深入研究，并鲜有从磨损时材料去除机制来评判滚刀磨损性能以及进行滚刀寿命预测。因此，本文重点研究滚刀的磨损机制并以此为依据建立滚刀磨损量的预测模型。

1 滚刀磨损形式及表面材料去除机制

1.1 滚刀磨损形式分析

滚刀磨损主要为正常磨损和非正常磨损，其中正常磨损是刀圈损坏的主要形式。对于正常磨损，已有研究表明磨料磨损是滚刀磨损的主要形式［8－9］。在实际工况中，滚刀刀圈不断滚压破碎岩石，同时刀圈表面受到岩石表面的凸起物以及破碎之后的硬质岩石颗粒的不断摩擦。图1为中铁西秦岭隧道中因磨损而更换下的滚刀刀圈表面在基恩士VHX－2000系列超景深三维显微系统中拍摄的三维磨损形态，图中箭头所指处为沟槽或细小的坑点，这是由于刀圈表面受到石英、矿岩、沙土等磨料的摩擦磨损，这些磨料与滚刀表面相互碰撞、碾压导致滚刀表面材料的流失。滚刀实际磨损形式也验证了滚刀的主要磨损形式为磨料磨损。

1.2 滚刀表面材料磨损去除机制

当前对于滚刀刀圈发生磨料磨损时刀圈材料的去除机制以及影响因素鲜有研究。磨料磨损一般是指硬的磨粒或凸出物在对零件表面的摩擦过程中，使表面材料发生损耗的现象［10］。在滚刀的破岩过程中，刀圈上承受着很大的压力，而且岩石强度越高，承受的压力越大。刀圈表面材料去除机制如图2所示。在滚刀贯入岩石时，岩石表面的凸起以及硬质颗粒挤压刀圈表面并压入刀圈，随着刀盘转动在刀圈上犁出沟槽，使刀圈材料直接去除(如图2(a))或者把刀圈材料犁到沟槽两边(如图2(b))，该机制为基于塑性的去除机制。当滚刀硬度低、塑性大时，在磨损当中更易于发生塑性去除，此时硬度直接影响着滚刀的耐磨性，并随着滚刀硬度增加而耐磨性增强。

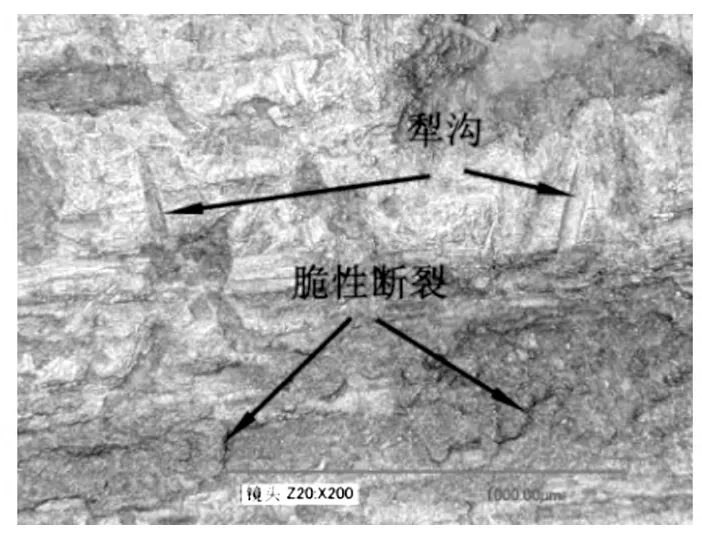
图1 刀圈磨损表面三维形貌Fig.1 Three － dimensional morphology of the cutter ring’s worn surface

图2 刀圈表面材料去除机制Fig.2 Material removal mechanism of cutter ring

随着刀圈受到岩石中硬颗粒的不断挤压使其内部裂纹不断扩展，当裂纹超过一定程度后形成断裂(如图2(c))，刀圈表面材料直接去除，这是滚刀磨损基于韧性断裂的去除机制。当滚刀硬度增加到一定程度时，塑性降低、断裂韧性降低，虽然滚刀抵抗塑性去除机制的抗磨性增强，但由于断裂机制导致的磨损显著增加。

上述结论可以很好地解释以下研究者的研究成果:金占明等［11］指出，当材料经受三体磨料磨损时，在某一临界硬度值以下，材料的体积磨损随硬度的增加而下降;当高于临界硬度以后，体积磨损却随材料的硬度增加而上升。赵金华等［12］指出，国产滚刀硬度高但耐磨性低，因为刀圈材料在实际工况下以大块断裂剥离为主，加速了刀圈的磨损，降低了材料的耐磨性能。

2 基于磨料磨损的滚刀磨损预测模型

由上述分析得出，滚刀正常磨损时主要磨损形式为磨料磨损，在磨料磨损过程中滚刀材料的去除机制主要为基于塑性的显微切削及犁沟去除机制，以及基于韧性断裂的微观断裂去除机制。在此将结合滚刀具体结果参数以及地质参数［13］，建立综合2种机制所引起的滚刀磨损的磨损量预测模型。

2.1 基于塑性去除机制的滚刀磨损量计算

Rabinowicz［14］提出简单的磨料磨损模型并导出定量的计算式，将磨损过程视为简单的滑动过程。磨料半径为r，在载荷P的作用下，压入较软的金属材料中，并在切向力作用下沿较软的金属表面滑动一定的距离L，犁出一条沟，其深度为X(如图3)。

图3 简化的磨料磨损模型Fig.3 Simplified model of abrasive wear

那么单位滑动距离磨损掉的金属材料体积，即被迁移的沟槽体积(图3阴影部分)，用下式可以算出:

式中:V为磨损掉的材料体积;r为磨料颗粒圆锥体半径;X为磨料压入材料内深度;L为磨料颗粒滑动距离。

根据文献［14］，磨料颗粒压入材料内的深度取决于压力的大小和材料硬度的比值，故有:

式中:˙Wa为塑性去除机制引起的磨损率;P为施加的法向载荷;H为材料的硬度;K为磨料磨损系数。考虑滚刀受力以及岩石特性、滚刀几何参数，采用科罗拉多矿冶研究院CSM模型［15］(如图4):

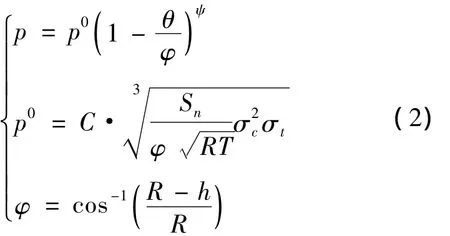
式中:φ为滚刀与岩石的接触角;p0为破碎区基本压力，θ为接触区里一点与滚刀中心线的夹角，其值为0～φ;ψ为刀尖压力分布系数;σc为岩石抗压强度;σt为岩石抗拉强度;C为量纲系数，C≈2.12;T为滚刀刀尖宽度;R为滚刀半径;Sn为刀间距;h为滚刀贯入量。

图4 滚刀作用岩石压力分布及CSM模型推导示意Fig.4 Contact stress distribution and CSM models indicate derivation

将式(2)代入式(1)，可得接触区中与滚刀中心线夹角为θ的点由塑性去除机制导致的磨损率:

滚刀每转动一圈，刀圈上每点参与破岩的轨迹一样，产生的磨损也一样，因此只需求出刀圈上一点在完成一次破岩过程中产生的磨损量与滚刀周长的乘积再乘上刀尖宽度，即滚刀转动1周产生的磨损量，由文献［6］可知，滚刀上每点破岩弧长S为:

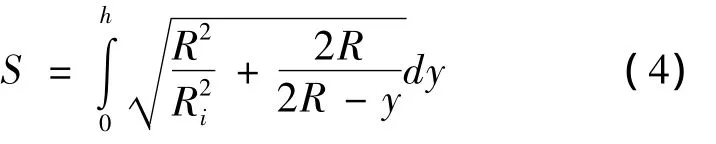
式中:Ri为第i把滚刀的安装半径;R为滚刀半径;h为贯入量;y为滚刀上一点到开挖面的深度。设滚刀滚动一圈，基于塑性去除机制产生的磨损量为Wa，由式(3)和(4)有:

2.2 基于韧性断裂去除机制的滚刀磨损量计算

考虑由裂纹扩展导致磨损表面的断裂剥离，Moore等［10］考虑单位面积里被磨材料表面在一定压力下受到磨料的滚压作用行程局部微裂纹的扩展，由断裂力学导出断裂磨损机制引起的磨损率公式为:

式中:˙Wb为单位面积里关于磨损距离的磨损率;K1为磨料形状及分布系数;P为压力;d为磨料平均直径;Kc为断裂韧性;H为硬度。

考虑滚刀受力以及岩石特性、滚刀几何参数，采用科罗拉多矿冶研究院CSM模型，将式(2)代入式(6)可得接触区中与滚刀中心线的夹角θ的点的磨损率˙Wb为:

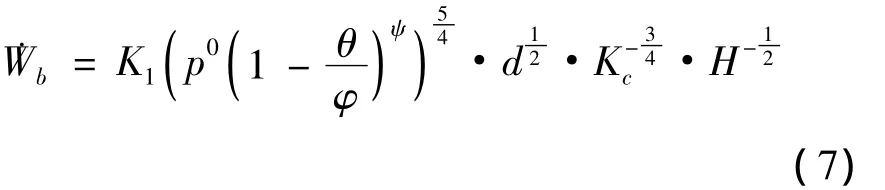
设滚刀转动一圈由断裂去除机制产生的磨损量为Wb，等于刀圈上一点完成一次破岩过程中产生的磨损量与周长的乘积再乘上刀尖宽，由式(4)和(7)有:

2.3 耦合塑性与韧性断裂去除机制的磨损计算模型

在滚刀实际工作中，刀圈的磨损主要由上述2种去除机制共同导致，建立滚刀磨损预测模型时必须综合考虑这2种机制导致的磨损量，这2种机制发生的比例又与材料自身的属性相关，前节分析可知，在低硬度高塑性时以发生塑性去除机制为主，在高硬度低韧性时以发生断裂去除机制为主。本文利用图像处理技术对滚刀磨损表面形貌SEM照片进行处理，来确定这2种机制所引起的磨损量的比值。

利用扫描电镜拍下磨损后的滚刀形貌的SEM照片，用灰度阀值分割法将磨损表面SEM照片处理成二值图，根据塑性去除机制与韧性断裂机制引起的磨损的形貌差别提取2种机制在磨损表面所占的面积比。设塑性去除机制所占比例为a，则断裂去除机制所占比例为1－a。联合式(5)和(8)，可得滚刀转动一圈后耦合这2种去除机制产生磨损量W1为:

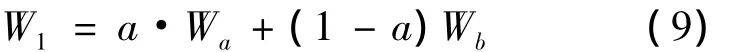
由于滚刀磨损后尺寸改变会引起磨损量的变化，因此需建立滚刀滚动一圈后体积减少量模型。为计算方便将不考虑滚刀刀尖边缘的圆角，根据滚刀截面图(如图5)设滚刀转动一圈所磨损掉的体积为V(图中阴影部分)，滚刀半径的减少量为x，则有:

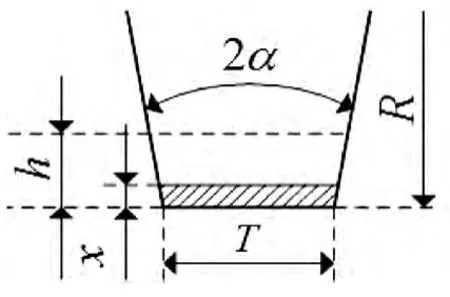
图5 滚刀截面图Fig.5 Sectional view of the cutter

式中:2α为滚刀刀刃角;T为滚刀刀尖宽度;R为滚刀半径;x为半径减少量。

联立式(9)和(10)有:W1=V，则可解得滚刀转动一圈后滚刀半径减少量x。滚刀滚动一圈后半径变为R－x，滚刀刀尖宽度变为T+2x·tanα，将其代入式(9)可求出第2圈的磨损量W2，进行k次计算可得第k圈的磨损量Wk。设TBM掘进距离为L，则第i把滚刀滚动的圈数n=，故第i

把滚刀总的磨损量W为:

3 滚刀磨损实验研究

3.1 实验原理与实验方案

实验采用H13钢加工成相似比为1∶4的小滚刀，热处理后硬度H=48 HRC，断裂韧性值Kc=21.3 MN·。小滚刀半径R=54 mm，不计圆角后刀尖宽度T=4.7 mm，刀刃角为2α =20°，根据文献［3］由于刀尖宽度较小取刀尖压力分布系数ψ=0.2。对磨岩石为大理岩，抗压强度为σc=100.33 MPa，抗拉强度 σt=5.69 MPa。

本实验采用多功能硬岩滚刀实验台(如图6)，模拟滚刀实际工作工况，在一定时间内让滚刀滚压岩石一定距离，测其磨损量。实验时先将小滚刀安装在小滚刀刀架上，把对磨大理岩放置于岩石槽内并用螺钉将其固定。由于刀尖宽度小，故设定滚刀贯入量h=1.5 mm，采用刀间距为10 mm。

图6 多功能硬岩滚刀试验台Fig.6 Multifunction test bench of hard rock cutter

实验时将小滚刀安装好，启动垂直油缸使滚刀侵入岩石到1.5 mm，然后启动纵向油缸推动岩石纵向进给，进给速度为3.5 mm/s，使滚刀被动破碎岩石30 min称其重量，完成1组实验。然后将滚刀重新安装在磨损机构上并重复以上实验过程，进行10组实验。

3.2 实验结果及分析

进行10组实验后，记录实验数据，通过测量破碎后大理石磨料，磨料平均直径d=83 um，根据文献［14］取磨料磨损系数K=8×10－2，磨料形状及分布系数K1=2。在磨损后的滚刀表面取10处样本进行扫描电镜分析，图7为1号样本表面图像，其中1号样本的SEM照片如图7(a)所示。

图7 1号样本表面图像Fig.7 Surface image of sample 1

运用最大方差法计算灰度阀值将其处理成二值图，再经边缘检测与轮廓提取后如图7(b)所示。塑性去除机制导致的磨损会在材料表面沿转动方向产生规则的具有方向一致性的长条形，而由韧性断裂导致的轮廓为不规则的无方向性的边缘，剔除断裂韧性导致的磨损轮廓后如图7(c)所示。在计算机中求出磨损形貌总面积为4 290个像素点，剔除断裂韧性导致的磨损形貌后总面积为4 038个像素点，因此塑性去除机制导致的磨损表面轮廓面积所占比例为94.1%。以同样的方法求出10组样品的数据如表1所示，由10组样品取平均值后得a=82.9%。

在计算滚刀磨损量的预测值时，统一采用g，mm，s，N作为基本单位，同时将硬度单位转换成N/mm2，该实验为线性切割故滚刀安装半径Ri=∞，因此式(5)中R2/R2i为0，滚刀转动圈数n=vt/πR，v为岩石进给速度，t为滚动时间，同时将(11)计算的体积磨损量转换成质量。将各参数代入式(11)计算，滚刀磨损预测值与计算值如表2所示。

表1 滚刀表面磨损形貌数据Table 1 Surface morphology data of worn cutter

表2 滚刀磨损实验计算值与实验值Table 2 Predictive data and experimental data of cutter

滚刀累计磨损量的实验数据与计算数据对比如图8所示。

图8 滚刀磨损预测值与实验值对比Fig.8 Comparison of predictive data and experimental data

根据实验磨损量与预测值比较(如图8)可知，滚刀磨损预测值与实验值基本趋势一致，实验值比预测值大是由于除了磨料磨损之外的其他形式的磨损。在60 min后磨损量增长趋于平稳，预测误差在20%以下，由于滚刀经过多次循环滚动后疲劳磨损量增加，故其误差绝对量逐渐增加。

4 结论

(1)TBM滚刀磨损过程中主要形式为磨料磨损，磨料磨损的去除机制主要为塑性引的显微切削与犁沟去除机制，及由韧性断裂引起的微观断裂剥离机制，在低硬度高韧性状态下滚刀磨损以塑性去除机制为主，在高硬度低韧性状态下以断裂去除机制为主。

(2)建立了滚刀磨损塑性去除与断裂韧性去除机制导致的磨损量计算公式，并通过对滚刀磨损表面的SEM照片进行图像处理来确定这2种机制所产生的磨损量之比，建立了耦合这2种去除机制的滚刀磨损量预测公式，并进行了实验验证，预测值与实验值基本趋于一致，在磨损量到达稳定后，预测误差在20%以内，预测结果基本吻合实验数据，能较准确地反映滚刀实际磨损。

［1］李慧丹，贾寒飞.全断面岩石掘进机盘形滚刀［J］.重工与起重技术，2006(1):19－20.LI Huidan，JIA Hanfei.Disc cutter of full face rock tunnel boring machine［J］.Heavy Industrial and Hoisting Machinery，2006(1):19 －20.

［2］赵丹，彭立敏，雷明锋，等.基于滑移线场的土压平衡盾构刀具切削扭矩研究［J］.铁道科学与工程学报，2013，10(3):37 －42.ZHAO Dan，PENG Limin，LEI Mingfeng，et al.Study on cutters cutting torque of EPB shield based on slip－line field［J］.Journal of Railway Science and Engineering，2013，10(3):37 －42.

［3］Rostami J.Development of a force estimation model for rock fragmentation with disc cutters through the oretical modeling and physical measurement of crushed zone pressure［D］.Mining Engineering，Colorado School of Mines.1997:34－45.

［4］Bruland A.Hard rock tunnel boring advance rate and cut-ter wear［R］.Trondheim:Norwegian Institute of Technology，1999.

［5］WANGLihui，KANGYilan.The energy method to predict disc cutter wear extent for hard rock TBMs［J］.Tunnelling and Underground Space Technology，2012(28):183－191.

［6］张照煌.全断面岩石掘进机平面刀盘上盘形滚刀磨损研究［J］.现代隧道技术，2007，44(6):32－36.ZHANG Zhaohuang.Study on the abrasion of disc cutters on full face rock tunnel boring machine［J］.Modern Tunnelling Technology，2007，44(6):32 －36.

［7］李笑，苏小江.盾构滚刀磨损的多元非线性回归预测［J］.辽宁工程技术大学学报，2009，28(2):281 －283.LI Xiao，SU Xiaojiang.Forecast of wear shield’s disc cutters based on multivariate nonlinear regression［J］.Journal of Liaoning Technical University，2009，28(2):281 －283.

［8］王旭，赵羽，张宝刚，等.TBM滚刀刀圈磨损机理研究［J］.现代隧道技术，2010，47(5):15－19.WANG Xu，ZHAO Yu，ZHANG Baogang，et al.Research on the ring wear mechanism of TBM disc cutter［J］.Modern Tunnelling Technology，2010，47(5):15 －19.

［9］胡怡，顾红星，张国利.TBM盘形滚刀的失效分析［J］.金属热处理，2007，27(1):55 －56.HU Yi，GU Hongxing，ZHANG Guoli.Failure analysis of disc hobbing for TBM［J］.Heat Treatment of Metals，2007，27(1):55 －56.

［10］Moore M A，Douthwaite R M.Plastic deformation below worn surfaces［J］.Metallurgical Transactions A，1976，7(12):1833－1839.

［11］金占明，邵荷生.塑性材料的三体磨料磨损转化机制［J］.摩擦磨损，1989，4(3):34 －39.JIN Zhanming，SHAO Hesheng.The mechanism transformation of three－body abrasive wear to plastic material［J］.Friction and Wear，1989，4(3):34 －39.

［12］赵金华，费学婷，袁国，等.国产与进口TBM滚刀刀圈显微组织与磨损机理的对比分析［J］.矿山机械，2012，40(8):120 －124.ZHAO Jinhua，FEI Xueting，YUAN Guo，et al.Comparison and analysis of domestic and imported TBM cutter ring in microstructure and wear mechanism［J］.Mining＆ Processmg Equipment，2012，40(8):120 －124.

［13］周援衡，王永和，胡萍.基于模糊集重心理论的软岩分类［J］.铁道科学与工程学报，2011，8(1):48－51.ZHOU Yuanheng，WANG Yonghe，HU Ping.Soft rock classification based on the theory of fuzzy set［J］.Journal of Railway Science and Engineering，2011，8(1):48－51.

［14］刘佐民.摩擦学理论与设计［M］.武汉:武汉理工大学出版社，2009:126－134.LIU Zuoming.Tribology theory and design［M］.Wuhan:Wuhan University of Technology Press，2009:126 －134.

［15］Jamal Rostami.A new model for performance prediction of hard rock TBMs［C］//Chapter 50，RETC Conference Proceedings，Boston MA，1993:794 －809.