数值方法中Runge-Kutta方法改进的探讨

赵 学 杰

(德州学院 数学科学学院，山东 德州 253023)

数值方法中Runge-Kutta方法改进的探讨

赵 学 杰

(德州学院 数学科学学院，山东 德州 253023)

根据一阶常微分方程数值解的收敛性与稳定性，从固步长的Runge-Kutta法出发，考虑变步长的Runge-Kutta法，讨论了3种改进算法，即折半步长Runge-Kutta法、Runge-Kutta-Fehlberg法和Zadunaisky方法.并且分别讨论了3种变步长的Runge-Kutta法的精度及效率.

数值解；Runge-Kutta法；变步长的Runge-Kutta法；自适应

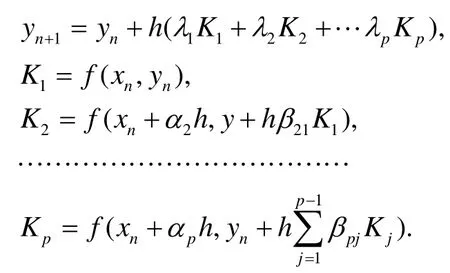
这是固定步长的Runge-Kutta法在不考虑步长变化下常用的一种方法，如果考虑步长h的变化呢?

考虑到计算的简便与精度，一般不考虑步长h的变化，如经典4阶 Runge-Kutta法，因为要做到合理选择步长h的大小是一种比较复杂的问题，它与问题本身及所选用的数值方法都有关系，单从每一步看，步长越小，截断误差就越小；但随着步长的缩小，在一定求解范围内所要完成的步数就增加了. 步数的增加不但引起计算量的增大[1]，而且可能导致舍入误差的严重积累.采取固定步长只是计算上的简便，在计算精度与效率上有较大的缺陷，在选择步长时，怎样衡量和检验计算结果的精度？如何依据所获得的精度处理步长[2]？

1 三种改进算法

考虑到如下两个问题：1) 步长h取的太小，便增加了许多不必要的计算量.2) 步长h取得太大，其计算度很难得以保证.因此，考虑给定一个数值解与精确解的误差容限，由这个误差容限缺点数值计算中步长的选择，在实际应用中，精确解是未知的，可以考虑从另一角度入手，即每走一步进程中，采取两个不同的方式，通过比较结果决定选取步长h.

自适应(即变步长h)的 Runge-Kutta方法有很多种，这里只讨论 3种：折半步长 Runge-Kutta法、Runge-Kutta-Fehlberg法和Zadunaisky方法.

1.1 折半步长Runge-Kutta法：

由(1)式与(2)式有：

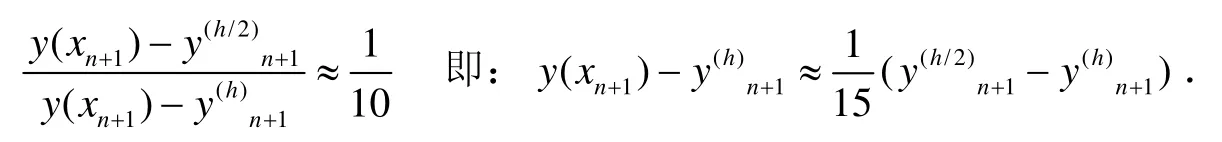
因此，我们得到变步长的Runge-Kutta方法的终止准则：

1.2 R-K-F(Range-Kutta-Fehlberg法)

Fehlberg于1970年提出用5阶Runge-Kutta法：

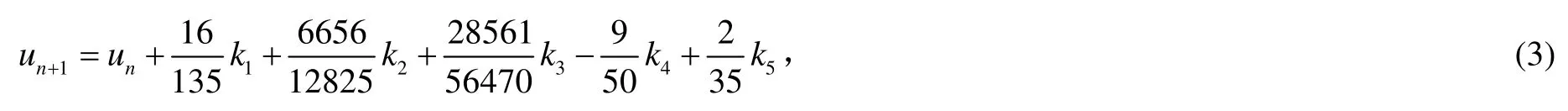
去估计4阶Runge-Kutta法：

其中：

称之为R-K-F法.

(3)式的局部截断误差为 o(h6)，即：.

(4)式的局部截断误差为 o(h5)，即：.

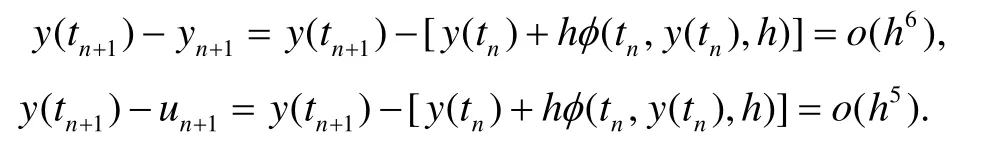
un+1的误差阶数比yn+1误差阶数高，因此，有可计算的误差估计：

于是，据(5)式及(6)式有：

利用 (8) 估计式选取合适的步长h，在 (7) 式中以qh代替h，其中q为正数，但不能太接近与0，再由(8)式有.假设误差容限TOL为给定的，则可选取q，使有：, 即：.实际使用时，常取

由于假定un=yn，(3)减去(4)得：

1.3 Zadunaisky方法

这种方法为Zadunaisky于1976年给出的一个技巧，它可以附属于任何一种p阶时间步进方法：

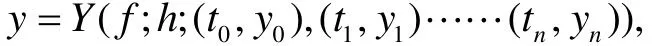
这种方法采取了另一种比较方式，即采用了p次插值多项式与4阶Runge-Kutta的结合，现在我们用数值求解常微分方程

假定已知p+1个值 yn-p,yn-p+1,… yn，它们不必为等距点上的值，构造一个 p次插值多项式 p(ti)满足p(ti)=yi(i = n - p,n - p + 1,… n)，并考虑常微分方程组

以下指出两个很重要事实：

1) 常微分方程组(11)只是原始方程组的一个小扰动，由于数值方法中为p阶， p(ti)为p+1个点的插值多项式，因此有 p(t) = y(t) + o(hp+1)，所以只要f充分光滑，则：

2) 常微分方程组(12)的是精确解为z=p，通过代换即得证.

利用相应的数值方法去逼近常微分方程组的解在zn+1的值，用的恰好是在计算yn+1使用到的条件：相同的初始值，相同的解非线性方程组的方法，相同的终止条件，结果为：

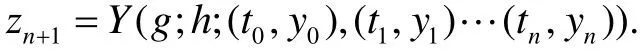
其中 g(t,z) = f(t,z) + [p'(t) - f(t,p(t)]，由于g≈f，可以假设zn+1的误差类似于yn+1的误差，得到估计式.

考虑p=4时的情况：开始时，只有一个初始条件，因此可考虑先用4阶Runge-Kutta法算出前4个点，再考虑使用Zadunaisky法.

存在常数k，使 τn+1= kh4, 即

假定误差容限TOL确定，则可由q来确定步长h的选择：

则可取q=1， y(tn+1)≈ yn+1，且下一步仍用这个h; 若

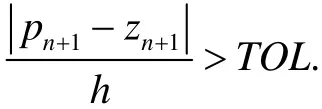
若不取yn+1，而是将步长缩小，为了确定步长缩小到不至于无限循环下去，我们给出了一个步长的下限，如hmin，若 h＜hmin，则终止计算，并给出终止的信号，当过小时，比TOL小到一定的程度时，则增大步长h.

2 结语

通过对上述问题的研究探讨，引入了3种变步长的Runge-Kutta法的计算方法，同时给出了精度及效率，作为妥协，如果能在计算过程中实时控制步长的大小，就可以在获得较高的计算速度的同时，保证较高的精度.

[1] 关治,陆金甫.数值分析基础[M].北京:高等教育出版社,1998:428-445.

[2] 李庆扬,王能超,易大义.数值分析[M]. 4版.武汉:华中科技大学出版社,2006:112-120.

[3] 诸梅芳,屈兴华,邓乃惠,等.计算方法[M].北京:北京工业大学出版,1988:215-219.

[4] 袁慰平,孙志忠,吴宏伟,等.计算方法与实习[M]. 4版.北京:清华大学出版社,2005:167-173.

[5] GERALD C F, WHEATLEY P O.应用数值分析[M].北京:机械工业出版社,2006:277-283.

(责任编校：李建明英文校对：李玉玲)

Discussion on Improving Runge-Kutta Methods in Numerical Analysis

ZHAO Xue-jie
(School of Mathematical Sciences, Dezhou University, Dezhou, Shandong 253023, China)

Based on the convergence and stability of the numerical solution of a differential equation, from a solid step Runge-Kutta method, it has considered variable step Runge-Kutta method. Three modified algorithm are discussed. They are step reduced by half Runge-Kutta method, Runge-Kutta-Fehlberg method and Zadunaisky method. At the same time, the accuracy and efficiency of variable step Runge-Kutta method are discussed.

numerical solution; Runge-Kutta Method; variable step Runge-Kutta method; self-adaption

O241.8

A

1673-2065(2014)04-0023-04

10.3969/j.issn.1673-2065.2014.04.006

2014-04-25

山东省自然科学基金项目(ZR2010Al019);山东省优秀中青年科学家科研奖励基金项目(BS2013HZ026)

赵学杰(1978-),男,河北枣强人,德州学院数学科学学院讲师,理学硕士.