智能传感器中神经网络激活函数的实现方案*

李宏伟, 吴庆祥

(福建师范大学 光电信息工程学院，福建 福州 350007)

0 引 言

目前，智能传感器多指嵌入了信息处理单元(如单片机，ARM，DSP)的传感器[1]，然而这些传感器中有很多都没有实现具备学习功能的智能。人工神经网络经历了几十年的发展，现已成为计算智能中较为活跃的一个领域，并可以在传感器的非线性校正、故障自诊断、多传感器信息融合等领域发挥重要作用，使运用此算法的传感器成为具有学习功能的智能传感器[2]。神经网络的优势主要体现在两方面，一是并行性，二而是强大的非线性信息的处理能力与学习能力。神经网络之所以能处理非线性信息，这在很大程度上归功于神经网络的激活函数。因此，实现神经网络的激活函数就成为神经网络硬件化的重要组成部分。Sigmoid函数是应用得最为广泛的一类激活函数[3]，并且考虑到现场可编程门阵列(FPGA)芯片可以灵活地嵌入到各种传感器中，本文研究FPGA实现Sigmoid函数的方法。

用FPGA实现此函数，常用的方法有查表法，分段线性逼近法、多项式近似法、STAM法、协调旋转数字计算机(coordinated rotation digital computer，CORDIC)算法等[5]。本文所采用的就是CORDIC算法与一种改进型高效除法器相结合的实现方案。

1 算法原理

Sigmoid函数的表达式为

(1)

若将其硬件化，主要有2个关键性问题:1)实现函数y=ex;2)完成除法运算。其中,CORDIC算法可以将复杂的指数运算转化为加减法运算和移位操作，适合在硬件上实现，在基于FPGA的信息处理系统中颇受关注。

CORDIC算法最早由Volder J[6]于1959年提出，20世纪70年代由Walther J[7]将此算法统一到双曲坐标空间中，并在图像处理、信号滤波等相关领域得到广泛应用。在双曲坐标空间内,逼近函数y=ex的原理如下

ex=sinhx+coshx.

(2)

可知，若要实现y=ex，只需实现coshx和sinhx，再将二者相加即可。假设某一向量的坐标为(coshθ1,sinhθ1)，然后将此向量旋转Δθ，则旋转后的新向量坐标为(coshθ2,sinhθ2)，其中

θ2=θ1+Δθ.

(3)

由双曲坐标空间的两角和关系得

coshθ2=cosh(θ1+Δθ)

=coshθ1cosh Δθ+sinhθ1sinh Δθ,

(4)

sinhθ2=sinh(θ1+Δθ)

=coshθ1sinh Δθ+sinhθ1cosh Δθ.

(5)

将式(3)、式(4)写成矩阵形式，有

(6)

又因为

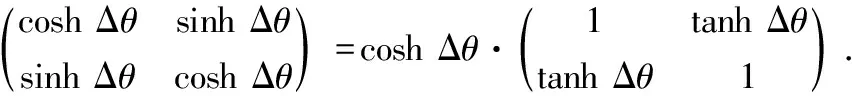
(7)

将式(5)与式(6)联立得

(8)

式(7)表明了相差Δθ的2个向量的递推关系。至此可以得到如下的结论：初始坐标为(coshθ0,sinhθ0)的向量，经过i次旋转，每次旋转的角度为Δθi，i次旋转后得到的新的向量坐标为(coshθ,sinhθ)，i≥1，再由式(8)的递推关系可得

(9)

现对Δθi作出如下规定

(10)

其中，“+”和“-”代表旋转的方向。由双曲坐标的相关公式可以推得

(11)

所以

(12)

当i→∞时，式(12)收敛于1.205 136，此值记作K。

2 系统设计

2.1 指数函数的逼近设计

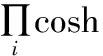
(13)

(14)

因此，在每次迭代的过程中只涉及加减法和移位操作。

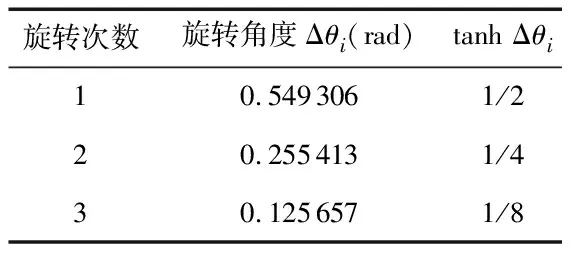
表1 前3次旋转的角度

2.2 除法器的设计

本文采用了一种经过改进的基于移位，比较与减法器的除法器设计方案。设置了4个寄存器变量，分别是被除数did、除数dis，商quo和余数rem。其中，被除数、商和余数的位宽都为N，除数的位宽为N/2。在除法器工作之前，先将余数初始化为0，即rem0=0。然后将被除数的最高位置于余数rem0的最低位，同时保持余数的位宽不变，rem0的最高位去掉，则新得到的余数rem1=0,0,...,0，did[N-1]。此时比较rem1与除数dis的大小，若rem1≥dis，则商的最高位置1，新的余数rem2=rem1-dis。若rem1≤dis，则商的最高位置0，然后将被除数的次高位置于余数rem1的末位，rem1的最高位去掉，以保证其位宽为N，新的余数rem2=rem1[N-2],rem1[N-3],......rem1[1],rem1[0],did[N-2]，以此类推，便可得到N位的商quo。现举例说明，被除数did=1010，除数dis=11，先将余数rem0初始化为0000，将did的最高位1置于rem0的末尾，去掉rem0的最高位，这样新的余数rem1=0001，因为rem1dis，所以,商的左数第三位置1，新余数rem4=rem3-dis=0101-11=0010。最后将did的末位0置于rem4的末位，去掉rem4的最高位，得到rem5=0100，rem5>dis，商的末位为1，最终的余数rem=rem5-dis，所得的商和余数分别为3和1。

上述除法器有两点局限性:一是被除数要大于等于除数;二是被除数的位宽要是除数位宽的2倍。在Sigmoid函数中，分子小于分母，因此,要对此除法器做出改进。

Sigmoid函数中，分子位置的1用48位的二进制数表示，即最高位为1，其余各位均为0，且将此分子看作整数。分母的计算结果是由24位的二进制数表示的，其小数点在左数第四位和第五位之间。这就相当于分子的小数点相对分母向右移了27位，因此，在利用改进方案计算出商值之后，商的低27位均表示小数部分。

3 测试与验证

利用CORDIC算法与高效除法器得到的Sigmoid函数的仿真结果如表2所示，其中,CORDIC电路单元经历20个时钟周期得到输出结果。除法器在软件上设置了一个48次的循环程序。从中可以看出：仿真结果基本可以精确到小数点后4位，在精度上可以满足一定的要求。表2给出了3组仿真值与理论值。

4 结 论

本文采用流水线的方式，在FPGA上实现了神经网络的Sigmoid激活函数，在精度上和速度上均达到了一定的指标要求，可以满足智能传感器的故障自我诊断等需求。

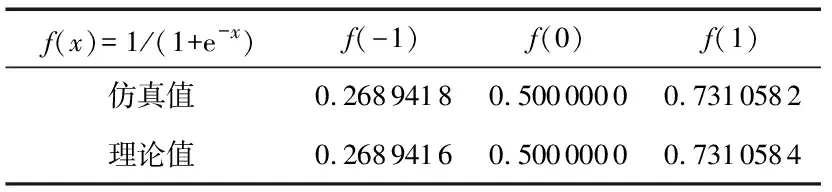
表2 3组仿真值与理论值

当然，如果要求更高的精度，可以适当扩展操作数的位宽和迭代次数，以满足传感器更高的智能化要求。下一步的工作是用这一函数来构建各种神经网络FPGA处理芯片，并应用到传感器信号的智能处理或基于FPGA的图像视频处理系统中。例如:在很多传感器中，都存在交叉敏感的问题，即传感器所测量的目标参数恒定时，而传感器的实际输出还会受到其他非目标参数的影响。为了解决交叉敏感的问题，可以采用多传感器信息融合的方法来剔除无用信息。此时，神经网络芯片模块便可植入到传感器当中，对输入的各种数据进行自适应学习，实现以学习为基础的数据融合，从而达到改善传感器性能的目的。

参考文献:

[1]刘君华．智能传感器系统[M]西安：西安电子科技大学出版社，2000：37.

[2]王 茜，董学人，尉吉勇,等．神经网络技术在智能传感器系统中的应用与发展[J] ．自动化仪表,2005,25(7):1-3.

[3]张智明,张仁杰.神经网络激活函数及其导数的FPGA 实现[J].现代电子技术,2008,281(18):139-142.

[4]Myers D J,Hutchinson R A.Efficient implementation of piecewise linear activation function for digital VLSI neural network-s[J].Electronics Letters,1989,25(24):1662-1663.

[5]张 萧，黄 晞，仲伟汉,等.Sigmoid函数及其导函数的FPGA实现[J].福建师范大学学报:自然科学版，2011,27(2)：63.

[6]Volder J.The CORDIC trigonometric computingtechnique[J].IRE Trans on Electronic Computers,1959,8(5):330-334.

[7]Walther J.A unified algorithm for elementary functions[C]∥Proc of Spring Joint Computer Conf,Berlin,1971:379-385.