高速轮轨速度极限探讨

朴明伟，王彦昌，方吉，兆文忠

(1.大连交通大学 机械工程学院，辽宁 大连 116028;2.大连交通大学 交通运输工程学院，辽宁 大连116028)*

0 引言

对于高速轮轨技术来讲，最高速度一再被刷新，其速度极限是否存在.或者说，高速轮轨是否存在提高其安全冗余的技术途径.在理论与实践上松平津证实了轨道车辆横向非保守系统［1］.日本新干线原始转向架，采用拉板式轴箱定位方式，以大阻尼抑制蛇行机制进一步提高车速，开创了200～250 km/h高铁运用新纪元.随后德国西门子公司再次推出了ICE3系列转向架，改善了300 km/h高铁运用的技术经济性，并成为了欧洲铁路最具代表性的高速车型之一.中国高铁在日系与欧系车辆引进技术的基础上，根据威金斯理论［2］，归纳并总结了基于抗蛇行频带吸能机制的稳定新理论［3］.随着里程2300 km的京广高铁正式开通，中国高铁也迈入300 km/h高铁的长交线路运营新时代.法国ALSTOM公司在TGV列车技术基础上，以5车编组的试验列车V150创造了目前最高时速的世界记录574.8 km/h.而京沪高铁型式试验，其最高试验速度也达到了480 km/h以上.高铁运用作为前沿技术探索，特别是商业运用的安全冗余，离不开坚实的基础技术应用研究.因此，中国高铁冲击600 km/h具有非常重要的现实意义.

以ICE3系列作为基准转向架，本文应用抗蛇行频谱特征匹配原则，进行了超高速转向架优配方案研究，并探讨了高速轮轨的速度极限以及冲击600 km/h的技术可行性.

1 抗蛇行频谱特征匹配原则

抗蛇行频谱特征匹配原则是在高铁运用实践与理论研究基础上提出来的，并作为高速转向架优配的指导准则.根据威金斯理论［3］，轮轨横向动态制衡关系是指车轮自旋蠕滑所产生的横向蠕滑力与重力刚度所形成的恢复力之间所存在的动平衡关系.与纵向蠕滑力不同，车轮自旋蠕滑对横向蠕滑力具有如下效应:在自旋蠕滑较小(≤0.6 m)时，横向蠕滑力呈现稳定地线性递增;如图1(b)所示，当自旋蠕滑较大时则出现快速衰减.

在较低等效锥度(≤0.25)的条件下，自旋蠕滑对横向蠕滑力效应稳定，且相当于“负阻尼”作用.随着车速提高或等效锥度增大，自旋蠕滑逐渐成为影响车辆稳定性能的主要因素之一.因而对于日系车辆来讲，采用大阻尼抑制蛇行机制无可厚非.但是问题在于:当进一步提速至300 km/h或轮轨磨耗等效锥度增大至0.25以上，蛇行振荡加快，大阻尼抑制蛇行机制也不再奏效了.因而称日本新干线运用存在轮轨磨耗遗留问题，即镟轮修程仅为20余万km，日系车辆技术服役寿命也仅为15年.

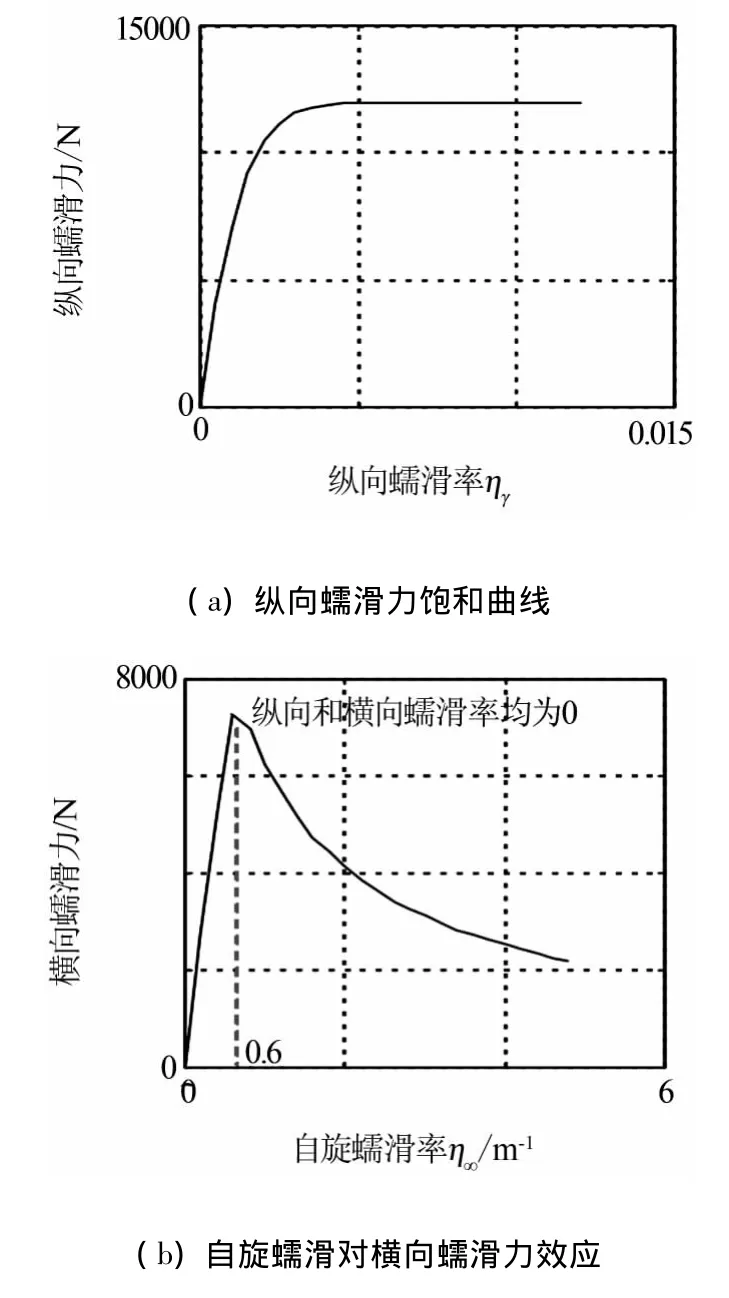
图1 纵向与自旋蠕滑对比

为了克服轮轨磨耗敏感性进而改善300 km/h高铁运用的技术经济性，德国ICE3系列转向架选用宽轮缘S1002G踏面，与CN60 kg钢轨匹配，其等效锥度0.166.而国际铁路联盟标准UIC518规定:对于新车性能验收型式试验，车速大于280 km/h，其等效锥度不得大于0.15.轮轨接触锥度越高，其磨耗指数越大.因而ICE3系列转向架采用了迫导向定位方式，特别强调了纵向定位刚度，高达120 MN/m.

抗蛇行频带吸能机制是指抗蛇行相位滞后与高频阻抗之间的自调节机制.根据MAXWELL模型，在小摄动位移假设下，抗蛇行减振器参数决定了其频带吸能特性.从抗蛇行减振器的技术实现角度，ICE3系列转向架采用了2项技术措施:一是以电机弹性架悬形成电机横摆模态，以降低蛇行振荡的参振质量;二是抗蛇行减振器冗余设计，即每架4个抗蛇行减振器.对于某动车组转向架原配，假设其抗蛇行串联刚度为X，线性阻尼为330 kN·s/m，其不同程度地表现出转向架稳定裕度不充裕问题，如构架振动报警故障和轴箱轴承温升报警故障，以及下凹型踏面磨耗特征等.而某长编列车转向架，其抗蛇行串联刚度为4.5 X，线性阻尼为440 kN·s/m，则出现高速晃车现象.因而现场调控将抗蛇行串联刚度降低至3.125 X.但是在隧道通过所形成的风荷侧向扰动作用下，则产生了高速列车稳定鲁棒性问题问题，如齿轮箱严重漏油甚至壳体裂纹.

抗蛇行频谱特征匹配原则是指实际蛇行振荡频谱特征与抗蛇行频带吸能特性之间的匹配关系准则.尽管采用了电机弹性吊悬，动车与拖车转向架蛇行振荡的参振质量也不尽相同，因而其实际的蛇行振荡频带也各不相同.也就是说，对于拖车来讲，其情况较为简单，车速与等效锥度是决定其实际蛇行振荡频谱特征的2个基本因素，因而在一定程度上，增大抗蛇行高频阻抗始终是提高转向架稳定裕度的积极因素之一.但是动车则较为复杂，在较低等效锥度下(0.166～0.230)，期望电机横摆释放部分蛇行振荡能量，而转向架蛇行模态则趋于自稳定;在较高锥度下(≥0.35)，刚好相反，期望电机横摆趋于自稳定，按照 IEC 61373规定保障电机振动安全.

与日系车辆不同，欧系车辆具有车体摇头大阻尼特征.抗蛇行高频阻抗越高，车体摇头大阻尼特征越明显，并对后位转向架稳定裕度产生非常不利的影响.因而过度增大抗蛇行高频阻抗将产生2个负面影响:一是在新车状态下或轮轨磨合期间，由于不能与电机横摆构成有效的运用耦合关系，动车后位转向架稳定裕度不充裕，在任何扰动或摄动影响下瞬间失稳并产生高速晃车现象，进而引起电机横摆自激振动响应，如瞬间横向颤振导致齿轮箱故障.二是在镟轮之前，电机横摆仍然趋于自激振动失稳，电机及其吊架的振动安全难以保障.由此可见，欧系车辆转向架统一优配不仅非常必要，而且也十分紧迫.

综上所述，抗蛇行频谱特征匹配原则就是协调解决欧系车辆2个基本不稳定问题的基本准则，不仅对目前高铁运用很重要，同时也是超高速转向架优配方案的指导准则.

2 超高速转向架优配方案

继承了日本拉板轴箱定位等部分转向架技术特征，庞巴迪公司推出了Zefiro 380高速列车，并采用了大功率永磁电机(PM Motor)新技术.根据上述技术特点，其可能存在如下2个技术不足:一是与日本新干线原始转向架类似，也可能存在轮轨磨耗遗留问题;二是大功率容磁电机的技术可靠性有待工程实践验证，如抗去磁能力和防尘保护等.鉴于此，本节主要以ICE3系列作为基准转向架，在如下轮配方案假设条件下，进行超高速转向架优配方案研究.

2.1 轮配方案

在轮轨横向动态制衡关系中有2个有利因素:即重力刚度所形成的恢复力和抗蛇行高频阻抗.鉴于目前抗蛇行减振器技术实现水平的制约，如德国ZF公司所提供的Sachs抗蛇行减振器，其最大液压刚度为4.5 X.因此，必须采用以增大轮轨接触锥度作为提高轮轨接触安全冗余的技术途径.

如图2所示，以缩小轨距方式给出超高速轮配方案，其主要技术特征如下:①CA:λe=0.22，宽轮缘S1002G，轨距G1 430 mm，其轮缘厚度较标准S1002踏面的增大3.5 mm;或者采用宽轮缘LM踏面，其轮缘厚度较标准LM踏面的增大2.5 mm，与标准轨距G1 435 mm的钢轨CN60 kg匹配，其等效锥度 λe约0.23;②CB:λe=0.35，踏面LM，轨距G1428 mm，模拟轮轨磨合后的轮轨接触状态;③CC:λe=0.43，踏面 LM，轨距 G1 427 mm，模拟轮轨稳定磨合后的轮轨接触状态;④CD:λe=0.52，踏面 LM，轨距 G1 425.5 mm，模拟镟轮之前的轮轨接触状态.

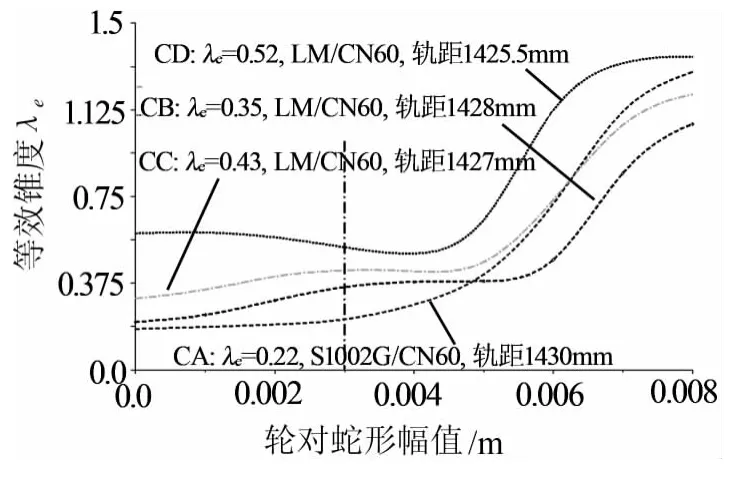
图2 超高速轮配方案

上述轮配方案仅在一定程度上体现实际磨耗轮轨匹配特征:

(1)新车状态下最小等效锥度为0.22;

(2)通过镟轮控制其等效锥度在0.52以下;

(3)轮配CA和CB较为理想，因为在蛇行幅值3 mm附近，其等效锥度锥度变化斜率较大，有利于提高非线性临界速度.

车轮踏面选用待定，其实际踏面磨耗特征也有待进一步跟踪调研.同时，高速车轮踏面应当具有宽轮缘技术特征，以便车轮踏面的经济镟修.

2.2 超高速优配方案

如图3所示，在转向架380BL其它参数不变的条件下，选取如下2个超高速方案进行对比:

(1)超高速方案Ⅰ:抗蛇行串联刚度优配值，3.75 X，其动车稳定性态见图3(a);

(2)超高速方案Ⅱ:抗蛇行串联刚度取4.50 X(现有产品)，并将电机减振器线性阻尼降至0.4Y(假设原配电机减振器线性阻尼为Y)，其动车稳定性态见图3(b).

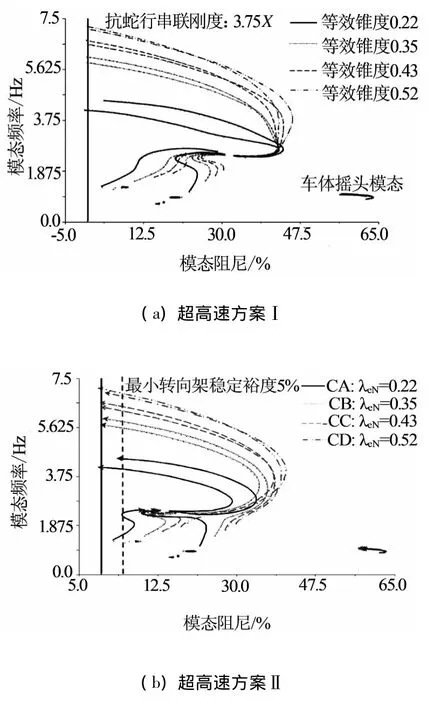
图3 超高速方案对比

相比之下，超高速方案Ⅰ，在较高等效锥度下电机横摆仍然趋于自激振动失稳;而超高速方案Ⅱ，则发生了转变，即电机横摆趋于自稳定.因而以超高速方案Ⅱ作为优配方案，并给出了动车与拖车非线性临界速度，见图4(a).根据UIC518所规定的安全极限，进一步确定了其运行速度空间，如图4(b)所示.

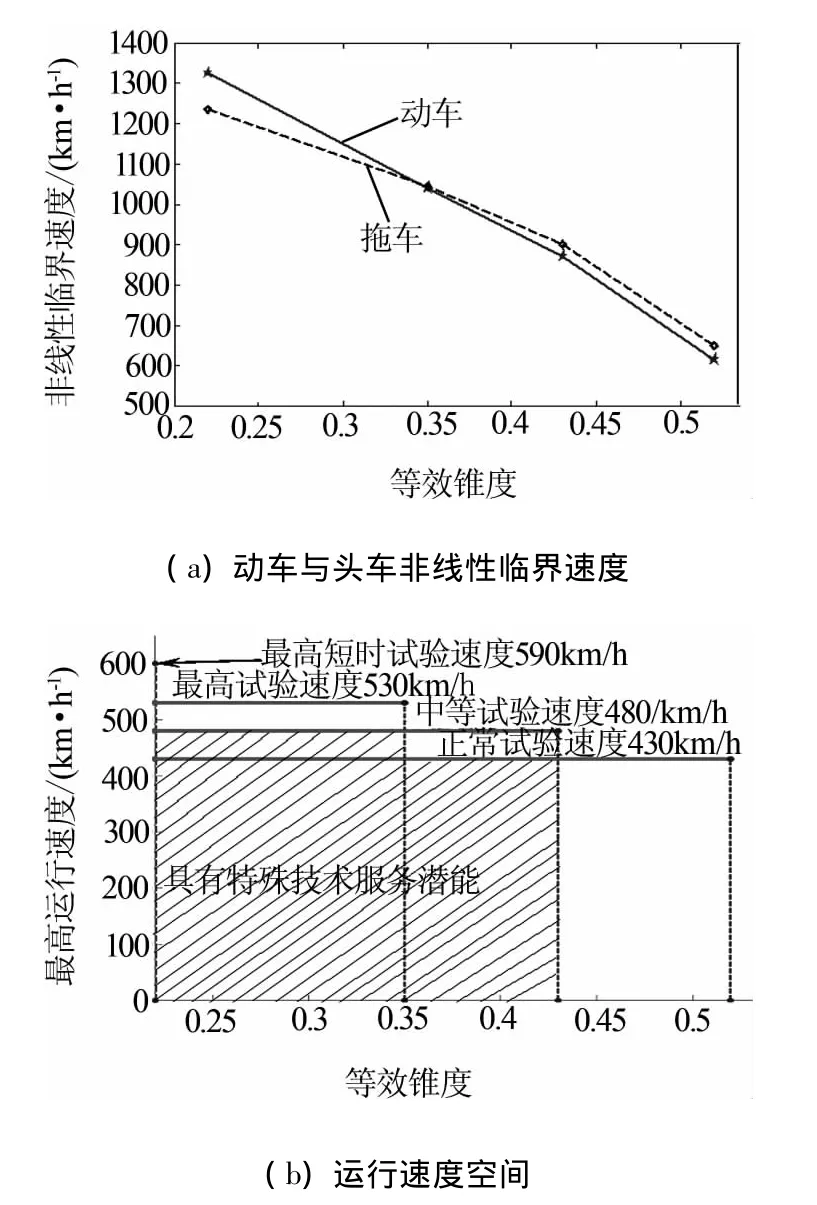
图4 超高速方案Ⅱ:非线性临界速度及其运行速度空间图

3 技术经济性分析

对于超高速列车来讲，其安全性应当作为首要考核指标.而技术经济性是指超高速轮轨新技术与社会经济发展的最佳切入点，或者说，两者之间是否具有相互补充与促进的“双赢”关系.下面，结合超高速方案Ⅱ，在如下3个方面进行技术经济性分析:抗蛇行减振器性能可靠性、车体横向振动响应带宽和电机横摆自激振动.

3.1 抗蛇行减振器性能可靠性

转向架稳定裕度是影响踏面磨耗的主要因素之一，因而抗蛇行减振器性能至关重要，否则如图5所示的踏面磨耗规律难以保障.对于动车400 km/h直线运行来讲，2位轮对的实际滚动圆半径与磨耗指数对比表明:

(1)在新车状态下存在轮缘侧磨，但是并不十分严重(≤200 N·m/m)，且随着等效锥度增大而逐步减轻，甚至达到无侧磨的程度;

(2)踏面磨耗，经过轮轨磨合，迅速增大，但基本控制在适度磨耗程度(即磨耗指数80 N·m/m左右);

(3)进入快速磨耗阶段后，下凹型踏面磨耗特征逐渐显示出来，如抗蛇振荡幅值(RMS)2.2σ逐步减小，镟轮之前仅为2.79 mm，且踏面磨耗率快速增长.

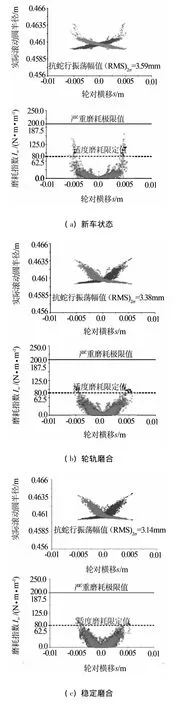
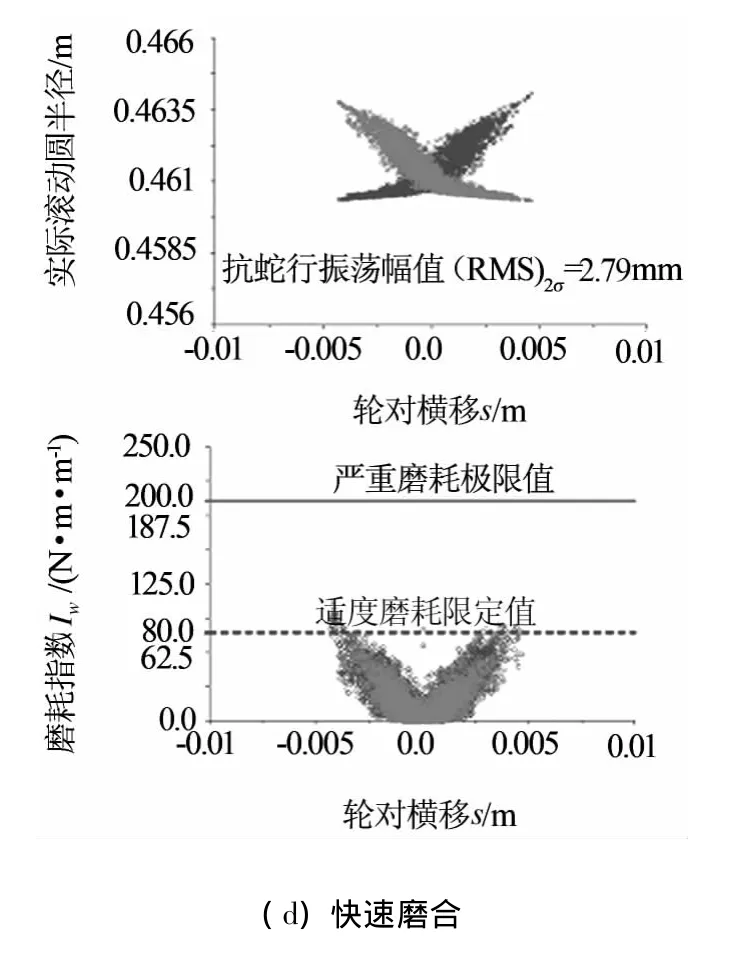
图5 动车2位轮对实际滚动圆半径与磨耗指数对比

由此可见，上述磨耗规律仍然取决于抗蛇行减振器性能可靠性，比如由于内部泄漏所造成的相位滞后，甚至抗蛇行减振器漏油等.否则，转向架稳定裕度就难以保障，车轮磨耗将极度恶化.目前，ZF Sachs抗蛇行减振器也仅在德国西门子公司的新一代高速列车上应用，据称其最高试验速度400 km/h以上.

3.2 车体横向振动响应带宽

在400 km/h直线运行下，如图6所示，等效锥度对动车与拖车车体横向加速度频谱响应特征的影响规律表明:在超高速运行下车体横向振动响应频带增宽，且轮轨磨耗敏感.但是车体垂向振动并无此类现象.

这是二系横向悬挂相位滞后所产生的非线性所导致的.也就是说，二系横向悬挂具有低阻抗小迟滞特性，在高频激扰作用下形成了相位滞后非线性，造成了大量高频振动的积累能量并传递给车体.由此可见，车体横向振动响应频带增宽，其主要危害在于车下质量是否发生横向耦合振动，并有可能造成裙板支架开裂等疲劳安全问题.这有待于刚柔耦合分析的进一步研究.

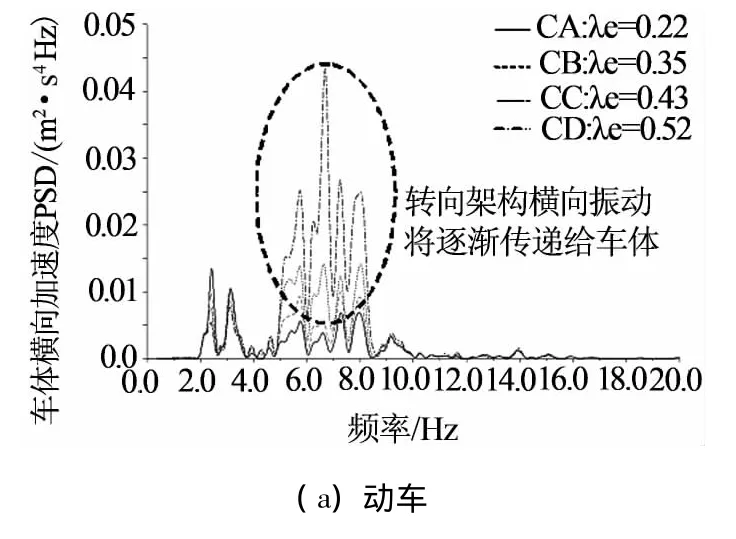
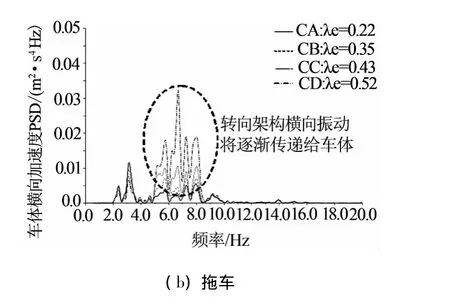
图6 等效锥度对车体后位横向加速度频谱响应特征的影响规律

3.3 电机横摆自激振动

电机横摆自激振动是超高速转向架的主要技术难题之一.如图7(a)所示，车速和等效锥度是影响电机横摆自激振动的2个主要因素.如图7(b)所示，在较高等效锥度下超高速方案Ⅰ与Ⅱ的电机横摆加速度对比可见:在电机横摆转变为自激振动状态后，其横向加速度有所减轻但效果并不明显.

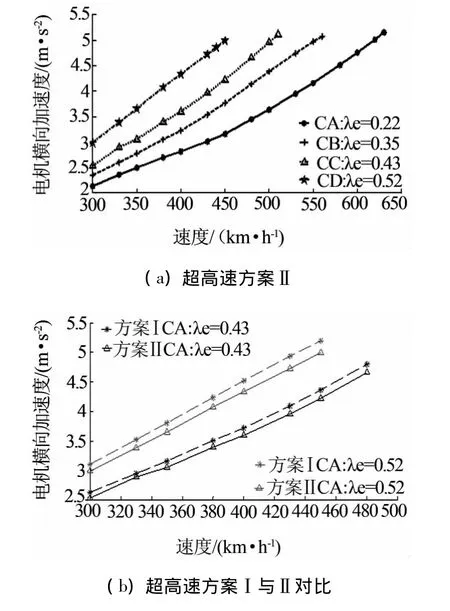
图7 等效锥度对电机横摆自激振动的影响规律

在超高速运行下，前位转向架的后部电机横向振动最为强烈，且呈现后摆倾向.这主要是抗蛇行高频阻抗抑制前位转向架摇头相位滞后所导致的.

综上所述，对于超高速转向架研制，或者400 km/h超高速运用来讲，存在上述3大技术难题.随着认知不断深入，这3大技术难题在技术与理论上可以得以解决，但是已经丧失了超高速运用的商业价值.若未来建设了超高速线路，如更大轨道超高满足其运行安全性等，如图4(b)所示，其阴影部分尚可有提供特种技术服务的潜能，如高速弓网关系试验研究、整编部队调动和超高速公务列车等.

4 冲击600 km/h的技术可行性

冲击600 km/h具有一定程度的技术可行性，其关键技术问题在于:是否克服车轮纵向蠕滑不稳定性以实现最大的牵引能力.

4.1 车体横向低频谐振

在直线500 km/h运行下车体出现横向低频谐振，约4Hz，且轮轨磨耗不敏感.在新车状态下，随着车速增高，无论动车还是拖车，其车体横向低频谐振有所增强，且频率也有所上升.

4.2 车轮纵向蠕滑不稳定性

随着车速增大，如图8所示，后位前导轮对的车轮纵向蠕滑低频谐振将迅速增强，并逐渐形成黏滑振动现象.当车速达到600 km/h时，后位前导轮对的车轮自旋蠕滑超过0.6/m的几率较高，如图9所示，因而后位转向架车轮有可能逐渐形成瞬间的纵向黏滑振动现象.因此，克服车轮纵向蠕滑不稳定性是冲击600 km/h的关键技术问题，同时也是高速轮轨速度极限的主要技术标志之一.

图8 后位转向架前导轨对的车轮纵向蠕滑

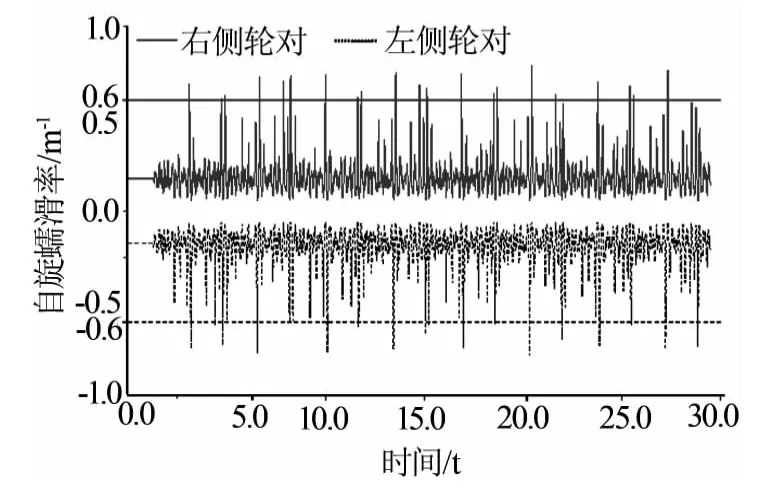
图9 后位转向架前导轮对的车轮自旋蠕滑

高速轮轨极限速度是一个有争议的热点问题.如上所述，威金斯首先提出自旋蠕滑，而三大蠕滑理论也有不同的假设.特别是自旋蠕滑是否具有饱和曲线特征，轮轨极限速度观点也不尽相同.若存在极限速度，则必须落实高铁经济运用.

5 结论

(1)以抗蛇行频谱特征匹配原则作为指导准则，根据基于抗蛇行频带吸能机制的稳定新理论，以ICE3系列作为基准转向架，通过必要的参数优配，制订了超高速转向架优配方案;

(2)动态仿真分析表明:400 km/h超高速运用存在3大技术难题:即抗蛇行减振器性能可靠性、车体横向振动响应频带增宽和电机横摆自激振动.随着认知的不断加深，上述3大技术难题可以得到解决.尽管如此，超高速运用已经丧失了其商业价值;

(3)冲击600 km/h不仅具有探索高速轮轨速度极限的现实意义，而且在技术上也非常可行.在500 km/h以上的超高速运行状态下，车轮纵向因黏滑而产生不稳定性，这一发现尚有待其它方面的确认.尽管如此，根据威金斯理论，车轮纵向蠕滑不稳定性也将作为高速轮轨速度极限的重要标志之一.

［1］IWNICKI S D.Handbook of Railway Vehicle Dynamics［M］.［s.n］:CRC Press，2006.

［2］WICKENS A H.FUNDAMENTALS OF RAIL VEHICLE DYNAMICS:GUIDANCE AND STABILITY［M］.ISBN The Netherlands:Swets＆ Zeitlinger，2003.

［3］朴明伟，梁树林，方照根，等，高速转向架非线性与高铁车辆安全稳定裕度［J］.中国铁道科学，2011，23(3):86-92.

［4］ MAZZOLA L，ALFL S，BRAGHIN F，et al.Limit Wheel Profile for Hunting Instability of Railway Vehicles［C］//Proc.of the Euromech 500 Colloquium:Non-smooth Problems in Vehicle Systems Dynamics，2008，Part 1，41-52，Springer-Verlag(ISBN 978-3-642-01355-3)，2010.

［5］CHARLES G，DIXON R，GOODALL R.Least Squares Method Applied to Rail Vehicle Contact Condition Monitoring［C］//Proceedings of the 17th World Congress，The International Federation of Automatic Control Seoul，Korea，July 6-11，2008.