移动平均趋势季节比率测算法在税收预测中的应用

□（辽宁税务高等专科学校 辽宁大连 116023）

预测是在对过去信息进行分析的基础上，找出其发展变化的规律，用以对未来进行推断的一门科学。税收预测从狭义的角度来说即是对税收收入的预测，是对一个国家（或地区）在未来某一时期可能的税收收入的测算，它是根据过去和现在相关的历史资料和数据对未来税收收入趋势的推测。税收收入预测是税源管理工作的重要组成部分，是提高税收收入工作的计划性和预见性、实行税源专业化管理的客观要求，在加强组织收入、完成税收收入计划、为领导科学决策和管理服务等方面起着非常重要的作用。因此对于税务部门而言，采用科学的税收预测方法，提高预测的准确率，对做好组织税收收入工作有着更为深远的理论和现实意义。

一、税收预测方法的分类

国家税务总局目前在进行税收预测时主要使用的方法有常规预测方法、统计学预测方法和机器预测方法等三类。

（一）常规预测方法

常规预测方法中包括层层上报预测法、历史数据经验预测方法和滚动预测模型等。

层层上报预测法是指税收统计部门采取的从税务部门最基层的税管员开始通过层层上报的方式，逐级汇总从而得到最终预测值的方法。由于基层税收管理人员对其管辖内的纳税人的了解程度较高，互动性较强，通常通过这种方法得到的预测结果可信性较高。其数据采集的方式主要有两种：一是每月上旬和中旬预测本月税收收入；二是每年11月和12月份预测全年税收收入，从而在一定程度上大大提高预测的精确度。

历史数据经验预测方法是根据全年中上、下半年或者季度税收比重加以测算的，通常税收收入在上、下半年间或者各季度间的比重存在一定的区间范围，可以通过计算近年来的该比重区间范围，估计全年税收收入，这个方法通常在季度或者半年预测时使用。需要强调的是按照此前几个月份的收入规模进行测算时，要注意剔除各月份中类似所得税汇算清缴等特殊因素的影响。

滚动预测模型的基本思路是通过以下步骤得以实现：一是利用历史资料找出修正的税收收入的月度分布曲线；二是利用预测年度已经实现的税收与修正曲线的数据相比较，求出实现税收的增长系数；三是利用实现税收的增长系数和经济预期增长速度加权求出税收年度增长系数；四是用税收年度增长系数乘以修正后的税收月分布曲线各月税收，求出预测年度各月税收；五是滚动调整。

（二）统计学预测方法

统计学预测方法可归纳为定性预测方法和定量预测方法两大类。

定性预测方法较适用于对缺乏历史统计资料或趋势面临转折时的情况进行预测，这种方法既可用于短期预测也可用于中、长期预测，应用时需要做大量的调查研究工作。

定量预测方法主要有回归预测法和时间序列预测法等。回归预测法主要包括一元线性回归预测法、多元线性回归预测法和非线性回归预测法等；时间序列预测法包括时间序列分解法、趋势外推法、移动平均和指数平滑法、自回归过滤法以及平稳时间序列预测法等。定量预测诸多方法的一个共同特点是需要搜集大量的历史数据，这也是这种预测方法中最费时费力的一项前期准备工作。

（三）机器预测方法

目前主要使用了神经元方法和支持向量机方法，这些方法无须更多的经济学解释，只需通过计算机及专业的分析软件在收集数据以及对数据预处理的基础上即可进行预测，它们通常是作为统计预测方法的辅助参考使用。

很显然，就方法的选择而言，在实际工作中不同的层级间、不同的时间（长、中、短期）状况下、根据不同的数据可以选择不同的预测方法。常规预测方法中的历史数据经验预测的方法经常被用于对税收收入的估算，而这一方法由于对经济变化及规律性把握不是十分准确而使其方法的估算并不很科学；而复杂的机器预测方法又需要我们掌握大量的数理统计及计算机相关知识，使其可操作性较差；统计学作为处理数据的一门学科，它的很多方法在税收收入预测中被越来越多的加以重视和利用。其中，回归分析法由于需要较为准确、及时地掌握影响税收变化的诸多经济数据才能在此基础上建立回归模型，因此实际应用过程中难度较大；如此一来，利用税务部门自己掌握的数据进行税收预测就成为最为可行和方便的办法，时间序列分析法中的很多方法正是这一思路的具体体现。

不同的数据特征下可以考虑采用不同的方法，其中很多时候数据的表现特征更适宜运用移动平均趋势季节比率测算这一方法。需要强调的是在利用统计模型进行预测时应满足以下条件：一是预测年度的经济发展趋势应与前几年保持同步；二是税收政策没有重大调整；三是税收征管水平没有明显提高或降低。如果有一个条件不能满足，那么利用模型进行预测的效果将大打折扣。

二、统计学中移动平均趋势季节比率测算方法介绍

移动平均趋势季节比率测算方法顾名思义是将移动平均分析、趋势分析和季节分析三种测算方法相结合而形成的一种统计分析方法。

随着时间的推移，数据的波动有上升也有下降，而且上升或下降的幅度也不相同。这种波动通常包括长期趋势变动、季节变动、周期变动和不规则变动。对于这类数据，在进行预测时，通常是先将各个因素依次分解出来，然后再进行预测。由于周期变动的分析需要有多年的数据才能发现其周期成分，实际工作中很难实现，因此我们采用的分析模型为：Y=T×S×I。这一模型表示数据的波动包含有长期趋势变动、季节变动和不规则变动。对于这类数据的预测方法很多，其中移动平均趋势季节比率测算方法较为常用且简便。具体计算方法和步骤为：

1.计算移动平均值（根据掌握的数据资料，如果是季度数据采用4项移动平均，则月度数据采用12项移动平均），从而剔除数据由于随机因素引起的不规则变动 （需要强调的是，偶数项的移动平均还需要进行二项移正平均）。

2.再将各月（季）实际值除以对应的趋势值，即Y/T。

3.将Y/T按月（季）排列，再分别按月（季）计算季节比率。

4.进行季节指数调整。加总各平均的季节比率，其总和应为12或4，如若不是，则需要计算调整系数，用调整系数分别乘以各月（季）的平均季节比率，就是所求的季节比率。

5.分离季节成分，以消除季节变动对数据的影响。

6.根据数据特点建立适当的预测模型并进行预测（这一预测模型是消除了不规则变动和季节变动后只反映数据趋势变动的模型）。

7.根据模型计算最终的预测值（用各预测值分别乘以相应的季节比率得到最终的预测值）。

三、统计学中移动平均趋势季节比率测算方法在税收预测中的具体应用

下面以某地区2009-2013年各月税收收入资料为例（见下表），将其按月排列，说明移动平均趋势季节比率测算方法的具体应用。

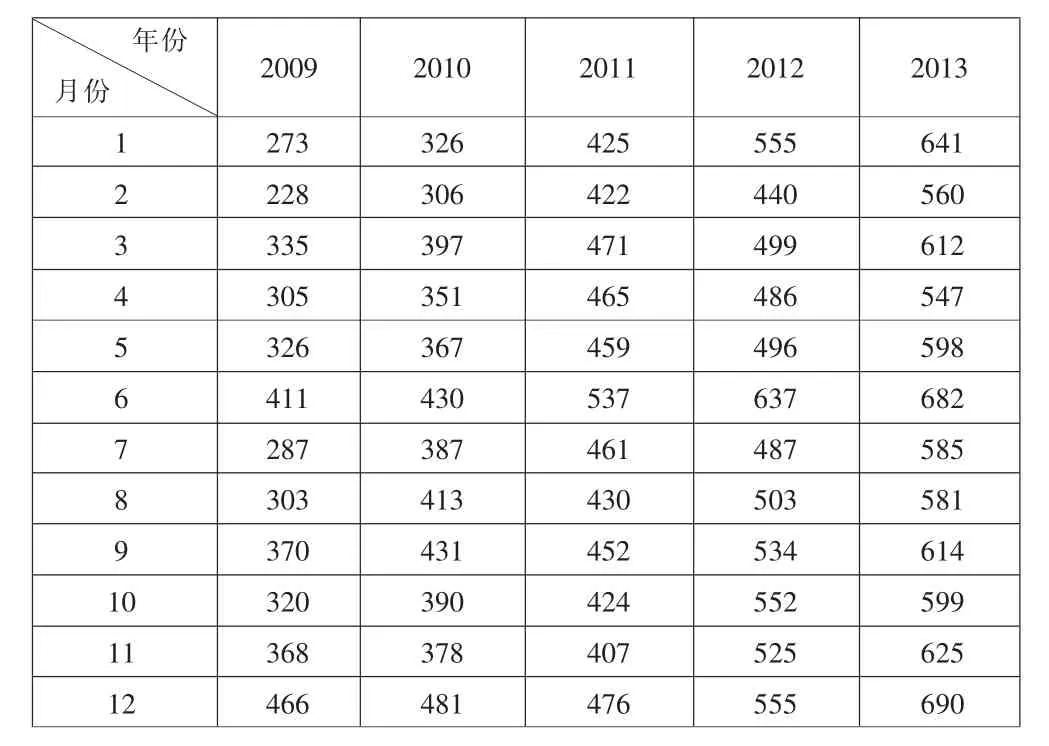
某地区2009-2013年各月税收收入 单位：万元

据相关数据资料，连续5年各月税收收入总的趋势是上升的，但也体现出较明显的季节变动和偶然因素引起的不规则变动。

第一步：计算移动平均值并将其移正，目的是消除不规则变动的影响。经过对原始数据采用12项移动平均所得移动平均值以及在此基础上进行的移正平均形成的新的数列值看，这种不规则波动被明显削弱了（见下图）。

修正平均后税收收入折线图

应当说明的是，采用移动平均法时，移动平均所取项数的多少，应视原数列资料的特点而定，原数列如有循环周期性波动，则应以循环周期的长度或其倍数作为移动平均的项数，否则趋势变动中就会包括周期变动在内。

再将各月实际值除以对应的移动平均值求得月份比值；然后就可以考虑对时间序列中的季节变动加以测算了。测定季节变动的重要指标是季节指数，测定的方法很多，这里采用按月平均法。

第二步：计算各年同月的月份比值的平均值及总的月份比值平均值，将各年同月的月份比值平均值与总的月平均值对比，得到各月的季节比率。

第三步：计算调整系数，得到最终的季节指数。

测算出最终的季节指数后，用各月的实际值除以对应的季节指数，就可以分离季节变动因素，使数列中的数据只表现其趋势变化。剔除季节成分后的税收收入的时间序列分布折线图具有明显的线性趋势，因此建立一元线性预测模型并用其来预测各月收入，而最终的预测值是要在一元线性预测模型预测值的基础上再乘以相应的季节指数才能得到。

通过上述分析我们发现，采用时间序列移动平均趋势季节比率测算法最大的优点就是能够通过历史数据找到反映时间序列本身的变化趋势，这种方法对于有明显周期性变化趋势且变动趋势相对稳定的数据资料进行短期预测效果较好。当然其局限性也是显而易见的，那就是要求有较多的数据资料以便对数据变动趋势做出较为准确的判断。

影响税收收入的因素很多，其中有些因素是可以量化的，有些是难以量化的，而任何宏观层面的税收预测模型只是把错综复杂的经济税收关系简单化、抽象化，它不可能全面地、真实地反映经济税收运行的全部情况。如何为这些影响因素建立合适的统计分析模型，并用于税收收入预测，以不断提高工作效率，形成规范的收入预测工作机制，是需要我们不断探索的课题。