二维分数阶扩散方程交替差分格式及其一致性

池光胜， 李慧玲

(1.山东凯文科技职业学院基础教学部，山东济南 250200;2.山东理工大学理学院，山东 淄博 255000)

二维分数阶扩散方程交替差分格式及其一致性

池光胜1， 李慧玲2

(1.山东凯文科技职业学院基础教学部，山东济南 250200;2.山东理工大学理学院，山东 淄博 255000)

研究二维有限域上的空间分数阶扩散方程的数值解法，通过移位的Grunwald公式对空间分数阶导数进行离散，得到Euler隐式差分格式。利用傅里叶变换理论证明了交替差分格式的一致性。

二维分数阶扩散方程; Euler隐式差分格式; 一致性

0引言

对于正常扩散，通常用传统的二阶对流-扩散(弥散)方程来描述，而反常扩散则是非马尔可夫(时间上)的非局域性(空间上)的运动，因此必须考虑运动过程的时空相关性，由此需要引入分数阶微积分，得到分数阶微分方程的反常扩散模型。对一维对流-扩散方程，于强等［1］给出了时间分数阶反应-扩散方程的隐式差分近似，并利用分数阶离散系数的特点，证明了这个隐式差分近似的无条件稳定性和收敛性。刘发旺等［2］利用拉普拉斯变换及H函数的性质，研究了一个时间分数阶对流-弥散方程的求解。郑达艺等［3］采用Grunwald改进型的离散方法对分数阶导数进行离散，构造出分数阶微分方程的差分格式，并证明了隐式格式是无条件稳定和收敛的。对于二维对流扩散方程，周璐莹等［4］对分数阶时间空间对流-扩散方程分别建立了差分格式，实现了数值求解。Chen S等［5］给出了一类求解二维分数阶渗透方程的差分格式的数值解法。上述研究均未对二维分数阶导数采用移位的Grunwald型离散方法进行分析，本文通过给出求解一个二维空间分数阶扩散方程的隐式差分格式，给出差分格式一致性的证明。

1 二维空间分数阶扩散方程的差分格式

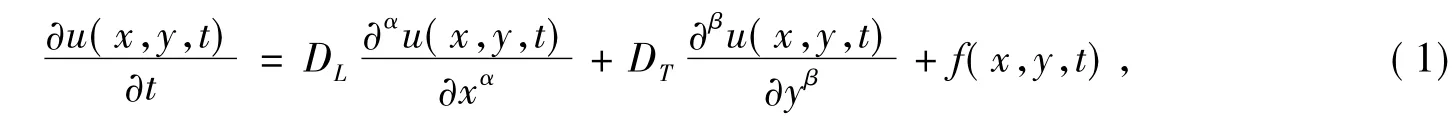
其中1＜α，β＜2，DL=DL(x)＞0是纵向扩散系数，DT=DT(y)＞0是横向扩散系数，f(x，y，t)是源项。首先对所求区域进行网格剖分:

对于二维空间分数阶扩散方程

其中hx和hy为二维空间步长，τ为时间步长。设uni，j表示 u 在(xi，yj)点处、时刻 tn时的近似值。对二维分数阶导数项有:

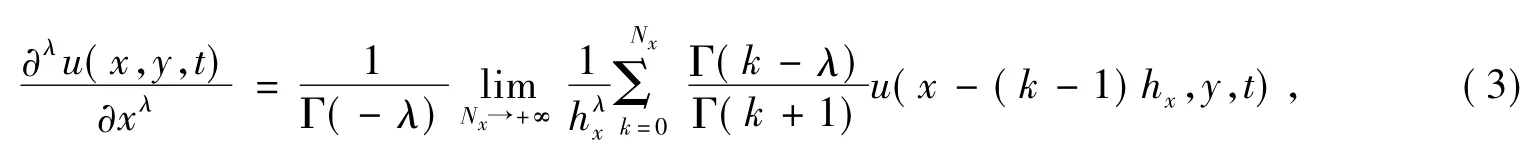
式中Γ(·)是伽马函数。记

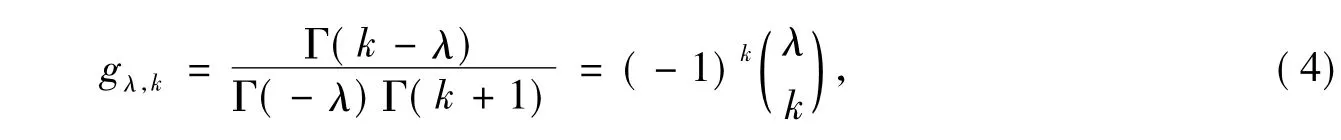
空间分数阶导数项可以用移位的Grunwald公式进行差分离散:

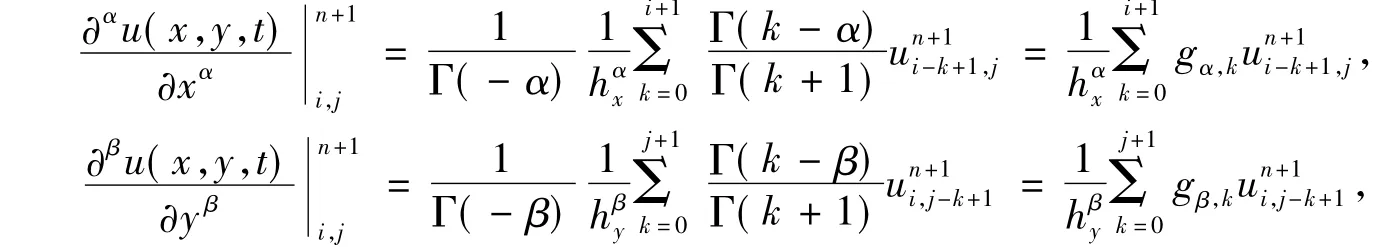
可得式(1)的隐式差分格式如下:

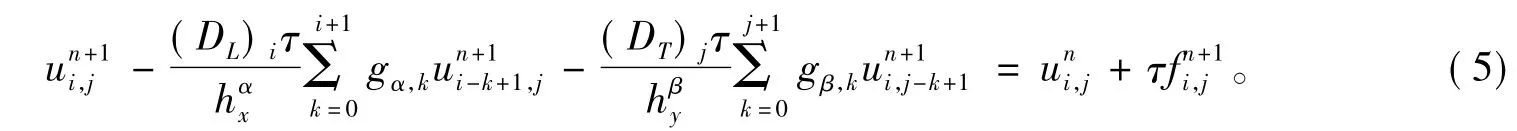
若定义分数阶差分算子:

则式(5)可写成如下算子形式:

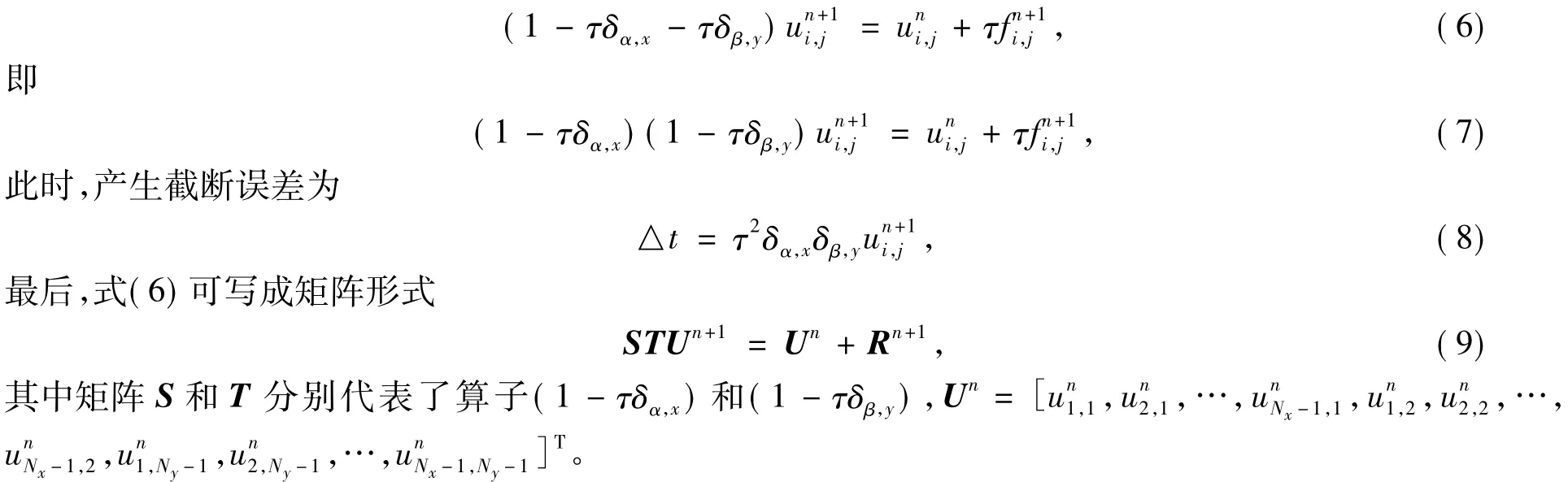
上述形式的ADI方法可通过以下迭代形式来求解。在时间tn+1处:

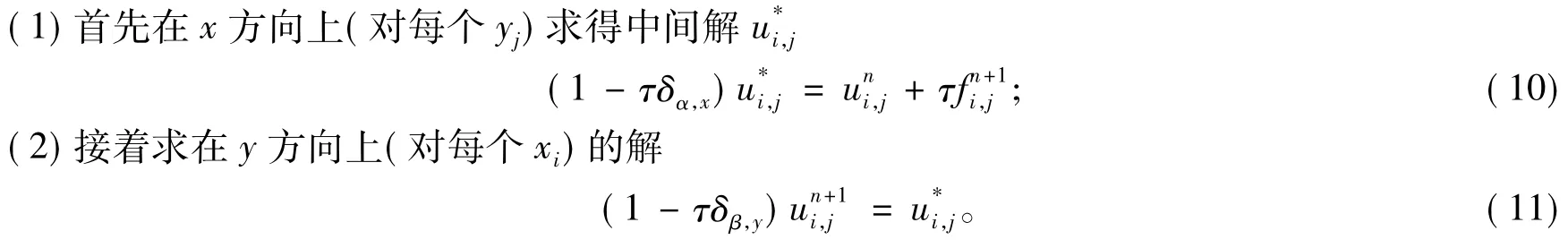
2 Euler差分格式的一致性

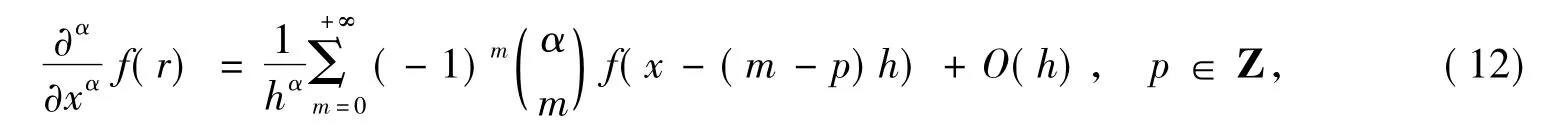
对于二维分数阶导数，若∀α，β＞0，p，q≥0且 p，q∈Z，空间步长 hx，hy＞0，也可以用如下式子来定义移位的Grunwald公式:

证明ADI交替差分格式的一致性:一维分数阶导数可用移位的Grunwald公式近似表达为［3］其中

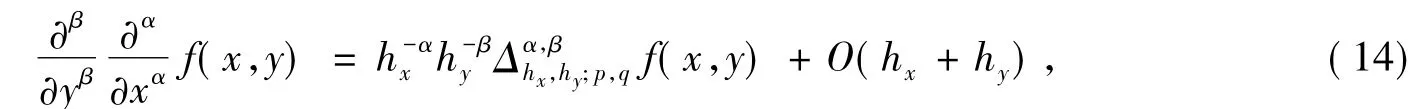
接下来将证明式(13)一致近似于混合分数阶导数。

定理 1 设 r＞α +β +3，r∈Z，则对任意的 f∈Wl，1(R2)，(x，y)∈R2有，函数f在ℓ1(R2)内有l阶的偏导数，并且在无穷远处，l-1阶的偏导数都为0。

证明 f∈ℓ(R2)的Fourier变换为:

证毕。

这表明A D I方法取代隐式欧拉算法后精度并没有减小，它的收敛精度为O(hx，hy，τ)。

3 数值算例

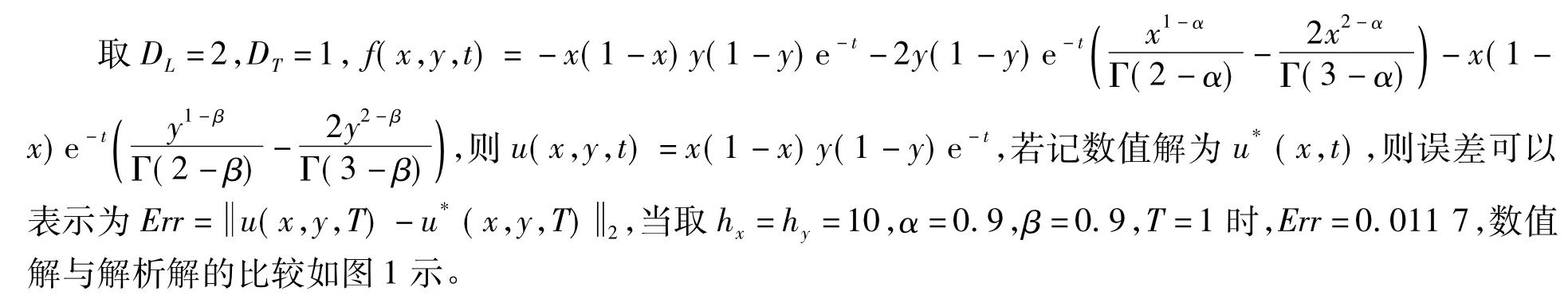
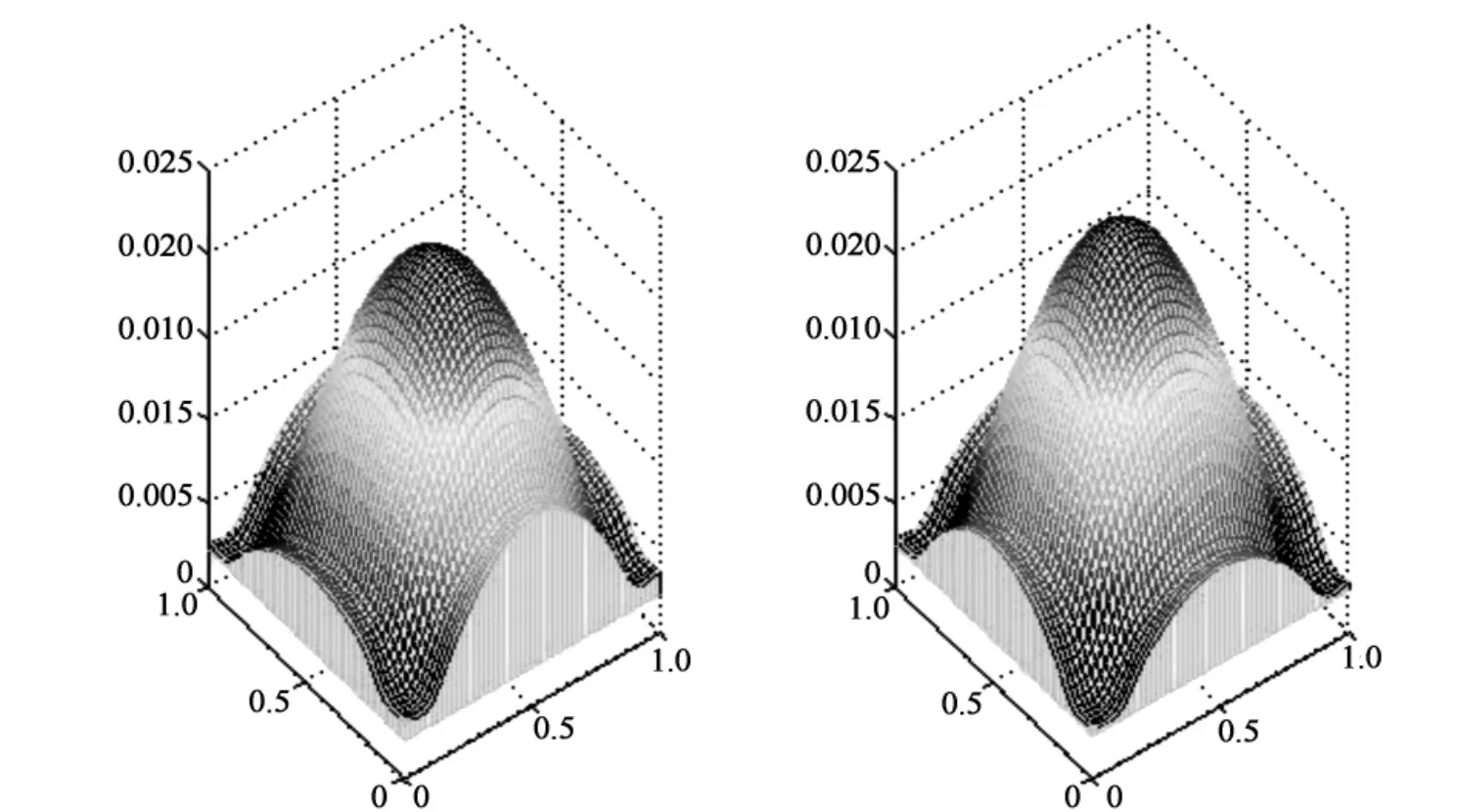
图1 数值解和解析解的比较图

通过计算结果可以看出，使用移位的Grunwald公式对二维分数阶导数进行离散建立的差分格式进行数值计算是有效的。

［1］于强，刘发旺.时间分数阶反应-扩散方程的隐式差分近似［J］.厦门大学学报:自然科学版，2006，45(3):315-319.

［2］LIU F，ANH V V，TURNER I，et al.Time fractional advection-dispersion equation［J］.Journal of Applied Mathematics and Computing，2003，13(1/2):233-245.

［3］郑达艺，刘发旺，卢旋珠.空间分数阶微分方程混合问题的数值方法［J］.莆田学院学报，2006，13(2):11-14.

［4］周璐莹，吴吉春，夏源.二维分数对流-弥散方程的数值解［J］.高校地质学报，2009，15(4):569-575.

［5］CHEN S，LIU F，TURNER I，et al.An implicit numerical method for the two-dimensional fractional percolation equation［J］.Journal of Applied Mathematics and Computing，2003，13(9):322-331.

［6］黄凤辉，郭柏灵.一类时间分数阶偏微分方程的解［J］.应用数学和力学，2010，31(7):781-790.

［责任编辑:魏 强］

Finite difference methods and its consistency for two-dimensional fractional dispersion equation

CHI Guang-sheng1，LI Hui-ling2
(1.Department of Basic Courses，Shandong Kaiwen College of Science ＆ Technology，Ji’nan 250200，China;2.Institute of Applied Mathematics，Shandong University of Science ＆ Technology，Zibo 255000，China)

In this paper we discuss the numerical method for two-dimensional fractional dispersion equation which fractional derivative can be approximated by the shifted Grunwald-formula on a finite domain.We get its Euler alternating directions implicit method which consistency can be proved by Fourier transform.

two-dimensional fractional dispersion equation; Euler implicit method; consistency

O242.1

A

1673-2944(2014)05-0064-04

2013-12-04

山东凯文科技职业学院自然科学基金资助项目(KW201209)

池光胜(1985—)，男，山东省淄博市人，山东凯文科技职业学院讲师，硕士，主要研究方向为数学物理问题;李慧玲(1987—)，女，河南省鹤壁市人，山东理工大学硕士生，主要研究方向为数学物理问题。