麻花钻螺旋槽数控加工中砂轮位置的自动搜索
李 铸 宇,张 伟,贺 凤 宝,胡 建 忠
(大连工业大学 机械工程与自动化学院,辽宁 大连 116034)
0 引 言
麻花钻的前刀面是螺旋面。它除了提供钻削加工中所需要的排屑空间,同时也影响主切削刃的形状和前角[1],是决定钻头切削性能的重要结构。螺旋槽的廓形传统上要求与形成廓形的刀具形线一一对应,并且形线精度要求严格[2]。这显然很难适应现代制造业出现的各种难加工材料。由于加工性能差别大,必须设计各种合适的槽型。目前数控制造中使用的硬质合金钻头,螺旋槽的加工只能用金刚石砂轮磨削。由于金刚石硬度高,修整砂轮费工费时,传统的设计方法显得困难而且成本高。
近年来,出现了模拟加工运动的直接法[3]。它是采用外形简单的圆柱砂轮,加工指定芯厚和径向前角的螺旋槽。芯厚的要求保证了钻头的刚度,前角则影响钻头的排屑和切削力等性能。同一片砂轮可以通过调整安装位置加工出不同的槽形,方法灵活,适应各种槽型,成为研究热点,但一些设计依靠经验数据确定砂轮加工位置[4];另一些采用粒子群(PSO)搜索算法,需要3 000次冗长的迭代计算得到结果[5]。砂轮的加工位置同时影响螺旋槽的芯厚和径向前角,使求解变得困难。
中心距和偏心距决定加工出的螺旋槽轮廓形状[3]。应用这个性质,提出一种新的有效解决上述难题的方法。首先,设定一个初始的中心距,满足芯厚的条件;在保证芯厚不变的条件下,调整砂轮加工位置,将满足芯厚和前角的条件分步实现;最后,用一维搜索的优化方法满足给定径向前角。
1 满足芯厚条件的初始中心距
如图1所示,以钻头的后端面中心为原点,建立全局坐标系{o:x,y,z},z轴和钻头轴线重合;动坐标系{o1:x1,y1,z1}附着在砂轮上,z1轴和砂轮轴线重合;z轴与z1轴之间的夹角β称为安装角;初始时刻,x1轴和x轴重合;z轴与z1轴之间的垂直距离称为中心距A。在加工的过程中,保持砂轮的方向固定不变,安装角β和螺旋参数p设定为常量。

图1 坐标系Fig.1 Coordinate systems
如图2,钻头的半芯厚(rw)定义为螺旋槽横截面曲线的内切圆半径;径向前角(γ)为外缘转点与圆心的连线,和该点螺旋槽轮廓曲线的切线之间的夹角。如图3圆弧砂轮,r是砂轮半径,ρ是圆弧半径。将砂轮垂直z1轴方向离散成直径不同的薄片。砂轮的左侧第1个薄片的直径最大,记为大圆Q。它到原点o1的距离称为偏心距T1。砂轮的加工位置由中心距A和偏心距T1确定。

图2 芯厚和径向前角Fig.2 Web and radial rake angle

图3 砂轮Fig.3 Grinding wheel
如图4,在初始位置,将大圆Q的圆心o2放置于毛坯轴线的正上方,这时偏心距T1=0。由于直径最大的这个砂轮薄片切入毛坯材料最深,它将决定加工出的螺旋槽的芯厚。当中心距A设定为

即可保证半芯厚rw。

图4 机床加工位置Fig.4 Machining position
2 调整中心距和偏心距满足芯厚条件
确定了初始中心距后,如果在调整中心距和偏心距的过程中,保持芯厚不变,则同时满足芯厚和前角两个条件,就能分步实现:第1步满足芯厚,第2步满足前角。
如图4,观察砂轮在垂直钻头轴线的横截面上的投影。以砂轮端面Q的圆心o2作为原点,建立辅助坐标系{o2:x2,y2,z2}。其中,x2和x轴重合;y2,z2轴分别和y,z轴平行。垂直z1轴方向对砂轮切片,每一个薄片都是直径不同的圆。每个砂轮薄片在螺旋运动中,将毛坯材料去除。
任意一个砂轮薄片在主视图平面x2o2y2中的投影是一个椭圆。整个砂轮薄片的投影就是这些椭圆相互叠加,形成的最外部的轮廓,用微分几何中平面曲线族的包络表示。在调整中心距和偏心距时,如果让钻头毛坯始终和这条包络曲线保持相等的距离,就能满足芯厚的条件。用砂轮圆弧部分的圆周角φ记录砂轮薄片的位置,砂轮薄片在平面x2o2y2中的投影用参数方程(椭圆方程)表示为
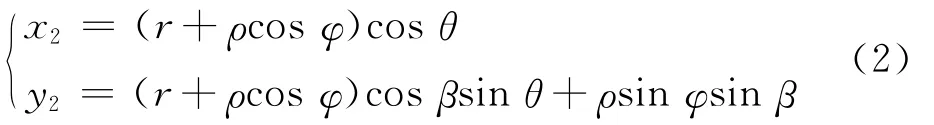
其中,θ是这个砂轮薄片上对应点的圆周角。所有砂轮投影的外部轮廓用平面曲线族的包络方程来表示[6]:

由式(2)计算偏导,包络方程(3)化简为
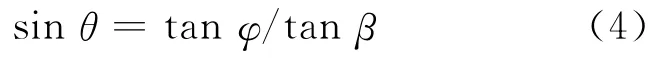
对于砂轮上任意一点对应的φ值,都可以由式(4)计算出它对应的包络角θ,将它代入式(2)中,得到包络点。由式(4)和(2)联立,所有包络点的连线构成了砂轮投影的边缘,记作投影曲线S1。
在图4中确定φ取值范围。平行于z轴作砂轮圆弧的切线,切点B将圆弧分为AB和BC两部分,切点B对应的φ等于β。AB段的所有砂轮薄片直径大于BC段砂轮薄片,BC段砂轮薄片的投影被AB段砂轮薄片的投影完全遮挡,砂轮AB段投影有效。因此,投影曲线S1上φ∈ [0,β]。
当砂轮绕毛坯轴线做螺旋运动时,砂轮在主视图中的投影曲线S1的形状始终不变。整个加工过程,从投影图上来看,就是曲线S1绕圆点o旋转。
3 利用相对运动将设计变量参数化
为了满足芯厚和前角的条件,以上第1步确定了砂轮和钻头相对运动的轨迹。这时,设定砂轮固定不动,钻头的中心沿投影曲线S1的等距曲线S2运动,保证芯厚不变。
投影曲线S1的等距曲线用微分几何计算[6]。砂轮的中心距A和偏心距T1用变量表示。如图4,在初始位置,在平面x2o2y2内移动钻头,这实际上是改变砂轮的中心距A和偏心距T1这两个变量的值。用移动后钻头轴线的坐标值xm和ym记录砂轮和钻头的相对位置:

在平面x2o2y2上,作曲线S1的等距曲线S2,它们之间的距离等于半芯厚rw。如果钻头的中心始终位于这条等距曲线S2上,这保证了砂轮和钻头中心之间半芯厚的关系,也就是钻头轴线的坐标值xm和ym满足曲线S2的方程。投影曲线S1用φ的参数方程表示:

为了推导等距曲线S2的方程,计算S1上面任意一点的法矢

其中,α′和α″分别表示α对变量φ的一阶和二阶导数。等距曲线S2用矢量表示

钻头中心的坐标值xm和ym满足式(8),写成坐标分量形式

将式(5)代入式(9)

由式(6)求导数,得到αx,αy,nx,ny的解析表达式。
任意给定φ值,由式(10)即可确定中心距A和偏心距T1。中心距的初值A=r+rw,偏心距的初值T1=0,即式(10)φ=0的情况,它是满足芯厚条件的初始解。
4 满足给定径向前角γ0
径向前角γ由螺旋槽在外缘转点处的切线,用数值求导的方法得到。大量的数值计算表明,当钻头的中心在图4中的第4象限变化时,径向前角γ为正值。以φ作为变量,构造一个目标函数f(φ):
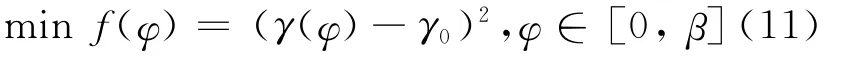
其中,γ0是给定的径向前角。如图5所示,φ∈[0,β]是目标函数f(φ)的一个单峰区间。采用一维优化中常用的0.618法求解,计算流程见文献[7]。

图5 目标函数f(φ)Fig.5 Merit function f(φ)
5 实 例
上述算法适用于带圆弧的直圆柱砂轮(图6)。钻头和砂轮尺寸见表1。设定初始的安装位置,选取砂轮后端,圆弧部分的最大直径作为大圆Q,将Q的圆心o2放置于毛坯轴线的正上方。由式(11)一维搜索得到参数φ,唯一确定中心距A和偏心距T1。螺旋槽的横截面曲线计算采用直接法[3]。螺旋槽的加工轨迹如图7(a),实际加工出的螺旋槽轮廓如图7(b)。

图6 直圆柱砂轮Fig.6 Cylindrical grinding wheel

表1 钻头和砂轮尺寸Tab.1 Dimensions of drill and grinding wheel mm

图7 加工轨迹和横截面轮廓Fig.7 Machining locus and cross-sectional profile
数值迭代值见表2。实际加工出的钻头和计算结果的比较见表3。程序迭代20次,达到ε=10-6收敛精度。实验结果表明,加工试件的芯厚和径向前角测量数据和设定值的误差小于2%。

表2 数值迭代值Tab.2 Iterative data

表3 钻头的设计值和测量值对比Tab.3 Comparison of the calculated data for the samples manufactured
6 结 论
(1)自动搜索确定砂轮安装位置,为麻花钻数控加工提供一种实用而且精确的方法。
(2)将砂轮安装位置的调整,看成在横截面投影曲线上钻头的相对运动,问题解决的策略是推导等芯厚的解析表达式,将同时满足芯厚和前角的条件分步完成。
(3)实际加工的沟槽横截面数据的测量和计算结果误差小于2%,证明方法有效。算法可直接应用于钻头开槽机的软件设计。
[1]倪志福,陈璧光.群钻:倪志福钻头[M].上海:上海科学技术出版社,1999:8-19.
[2]KANG S K,EHMANN K F,LIN C.A CAD approach to helical groove machining—I.mathematical model and model solution[J].International Journal of Machine Tools and Manufacture,1996,36(1):141-153.
[3]ZHANG Wei,WANG Xianfeng,HE Fengbao,et al.A practical method of modelling and simulation for drill fluting[J].International Journal of Machine Tools and Manufacture,2006,46(6):667-672.
[4]KIM J H,PARK J W,KO T J.End mill design and machining via cutting simulation[J].Computer-Aided Design,2008,40(3):324-333.
[5]KARPUSCHEWSKI B.Automatic search for wheel position in flute grinding of cutting tools[J].CIRP Annals-Manufacturing Technology,2011,60(1):347-350.
[6]PATRIKALAKIS N M,MAEKAWA T.Shape Interrogation for Computer Aided Design and Manufacturing[M].New York:Springer,2002:316-318.
[7]LUENBERGER D G,YE Y.Linear and Nonlinear Programming[M].New York:Springer,2008:216-219.

