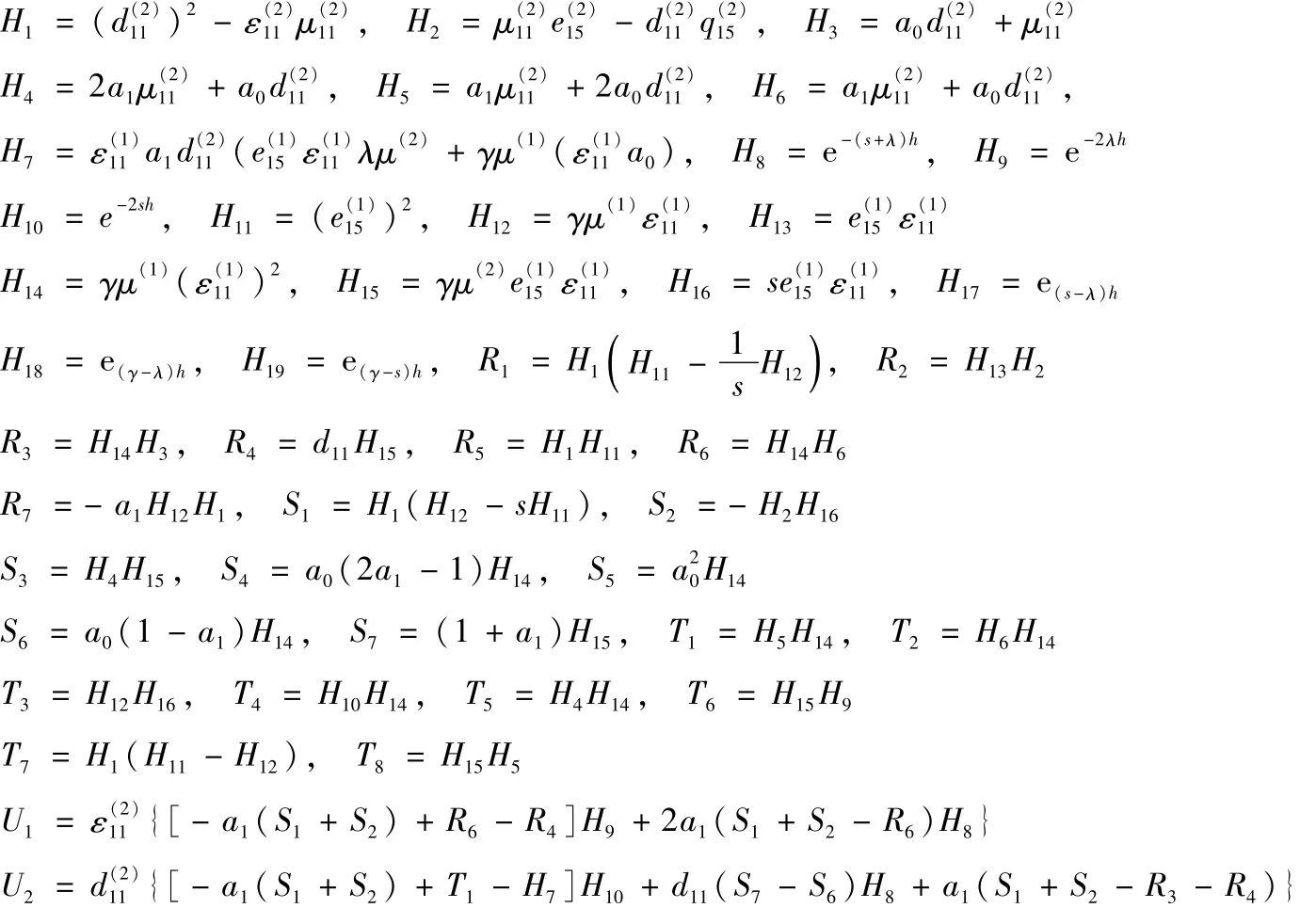压电拼接电磁复合材料中裂纹对SH波的散射

杨 娟，李 星

（（1.宁夏大学 数学计算机学院，银川 750021；2.宁夏大学 民族预科教育学院，银川 750002）

电磁材料作为一类多功能材料，因其特有的电磁耦合效应在电子技术、超声技术、智能工程及其它先进智能结构中得到广泛应用。在电磁结构设计中对其缺陷研究意义十分重要。

裂纹为常见缺陷，预存于器件中或器件使用时因外荷载产生。随探矿技术、无损检测技术、雷达及声纳技术发展及对工程结构在动态载荷作用下问题研究，弹性波散射理论研究引起普遍关注。文献［2－3］研究弹性复合材料中裂纹对SH波的散射。文献［4］研究压电纤维、弹性材料界面曲线型裂纹对反平面剪切波散射作用。文献［5］研究正交各型异性功能梯度材料中裂纹对SH波散射。诸文献均假设弹性波垂直入射，与实际情况不符。文献［6］利用对偶积分方程方法研究了功能梯度压电压磁材料中裂纹对以任意角度入射的SH波的散射。文献［7－8］考虑限制导通边界条件下，假设SH波以θ角入射，利用Copson方法研究了功能梯度压电带拼接半无限大压电材料及功能梯度压电层拼接半无限大功能梯度材料中裂纹对SH波的散射。文献［9］采用积分方程方法研究了功能梯度材料涂层下压电底层中裂纹对SH波的散射。，现在还未见到有关压电拼接电磁复合材料中裂纹对SH波的散射研究问题的报道。

本文利用积分变换技术结合求解对偶积分方程Copson方法研究压电材料拼接电磁复合材料中裂纹对以θ角入射的SH波散射。用Fourier变换将混合边值问题求解转化为对偶积分方程求解。获得裂纹尖端应力强度因子、电位移强度因子及磁通量强度因子。通过数值算例分析裂纹长度、裂纹到界面距离、入射角及波数对标准应力强度因子影响。

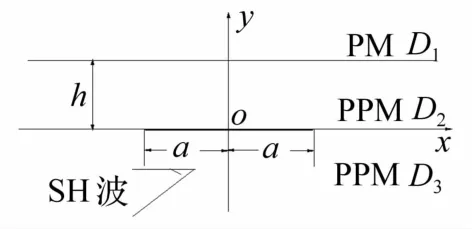
图1 压电材料粘接于电磁复合材料中裂纹对SH波散射的几何模型Fig.1 Geometry of scattering of the SH wave on a crack magnetoelectroelastic composites bonded to a piezoelectric material

1 问题描述

考虑的问题见图1，压电材料粘接于下半平面为半无限大电磁复合材料，内含长2a裂纹，上半平面为半无限大压电材料。xoy平面为各向同性面，与之垂直方向（z向）为极化方向。为描述方便，将结构分三个区域：裂纹以下为区域D3，裂纹至界面为区域D2，裂纹至界面距离为h，界面以上为区域D1。

SH波以θ角入射、作用于裂纹时，应力状态为反平面剪切，属断裂力学意义的Ⅲ型裂纹问题。不为零位移仅有一个，即 w（x，y，t）为x，y的函数，t为时间变量。由波的叠加关系可知总波场、入射场及散射场关系为

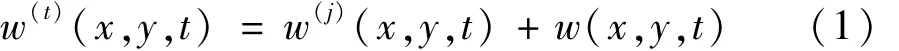
式中：上标（t），（j）表示总位移场、入射场；w（x，y，t）为散射场。

压电材料本构方程表示为

式中分别为压电材料应力、电位移、电势、剪切模量、压电常数及介分别为电磁复合材料应力、电位移、磁通量、电势、磁势、剪切模量、压电系数、介电参数、压磁耦合系数、电磁耦合系数及磁导率。图1中 k＝2，3分别对应 D2、D3区域。

设入射波为平面谐波，入射波形式为

因入射波、散射波时间因子相同，散射波场可写为

2 问题转化及对偶积分方程获得

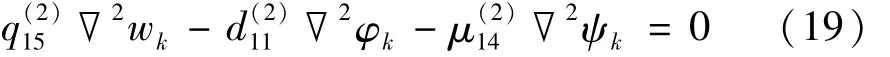
问题的边界条件为式中：2＝2x2＋2y2为二维 Laplace算子；ρ（1）为压电材料密度；ρk为电磁复合材料密度；k＝2，3。

式（15）～式（19）经傅里叶变换后的解可假设为

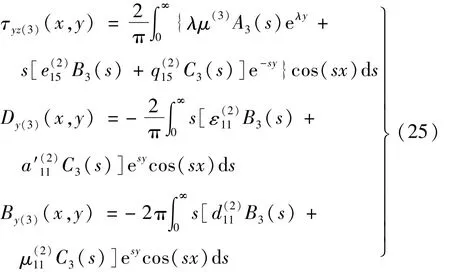
定义裂纹上下表面位移差为

将式（21）、（22）代入式（26），并经 Fourier余弦变换，得

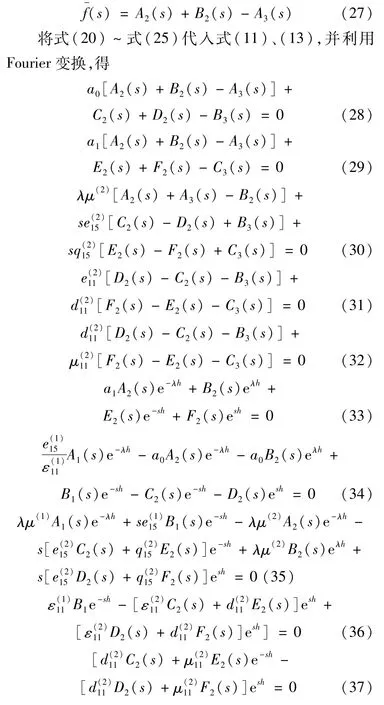
求解式（27）～式（37）获得 A1（s），B1（s），A2（s），B2（s），C2（s），D2（s），E2（s），F2（s），A3（s），B3（s），C3（s）的解 （见附录），并利用边界条件（11）得对偶积分方程为

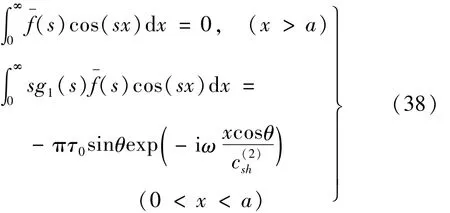
式中：g1（s）为已知函数，见附录。

3 对偶积分方程求解

式中：J1（ ）为第一类一阶Bessel函数。

将式（40）代入式（24），考虑裂纹尖端附近应力、电位移及磁通量在s→∞处奇异性，得y＝0时的应力、电位移、磁通量主部表达式为

定义标准化应力强度因子［10］为

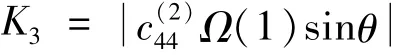
4 数值算例及讨论

设（图1）结构中压电材料、电磁复合材料分别为PZT－4、BaTiO3－CoFe2O4，其结果见图2～图4。

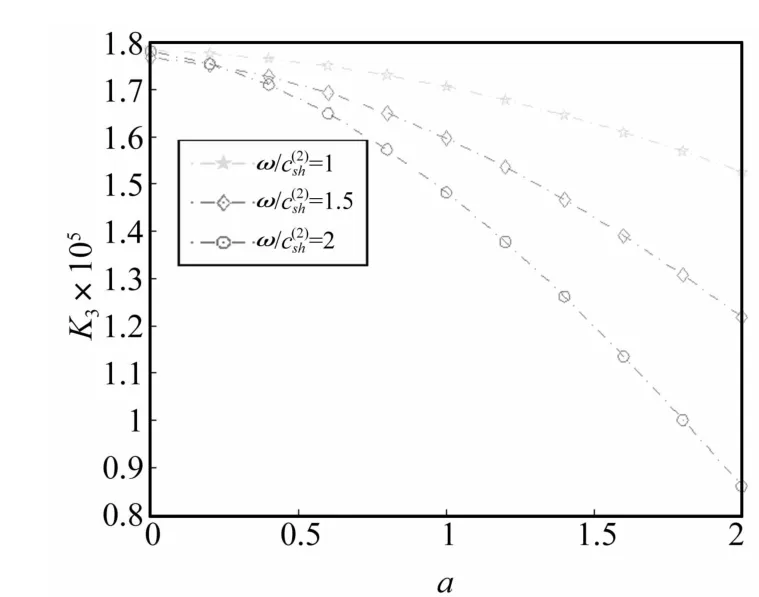
图2 不同aω时标准化应力强度因子K3随a变化关系Fig.2 Variations of the normalized stress intensity factor K3 with a for different aω

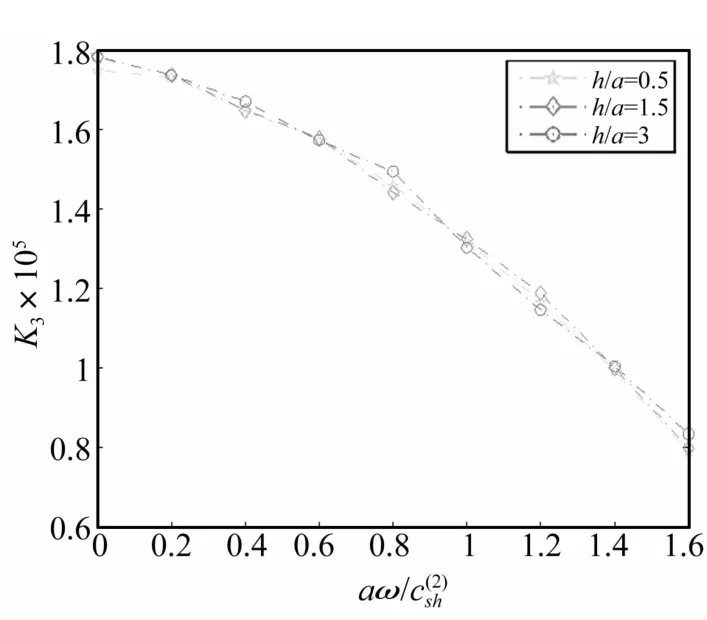
图3 不同h／a时标准化应力强度因子K3随aω／变化关系Fig.3 Variations of the normalized stress intensity factor K3 with aω／ for different h／a

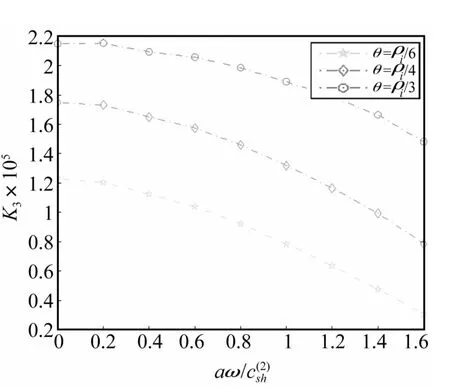
图4 不同θ时标准化动应力强度因子K3随aω／c（2）sh变化关系Fig.4 Variations of the normalized stress intensity factor K3 with aω at differentθ

（1）图2为波数aω／c（2）sh变化时裂纹长度a对标准动应力强度因子影响（h／a＝0.5，θ＝pi／4）。由图 2看出，aω越大标准动应力强度因子越小；aω一定时标准动应力强度因子随a的增大而减小，而标准动应力强度因子在裂纹长度为0～0.3间即较接近。工程中可通过检测裂纹长度变化预防因裂纹扩展造成的工件失效。

（2）图3为不同裂纹至界面距离 h／a时波数aω对标准动应力强度因子影响（a＝0.5，θ＝pi／4）。由图3看出，h／a对标准动应力强度因子影响不明显。工程中适当控制裂纹至界面距离有利于提高材料的抗断裂能力；h／a一定时标准动应力强度因子随aω／的增大而减小。

（3）图4给为入射角 θ变化时波数aω／对标准动应力强度因子影响（h／a＝0.5，a＝0.2）。由图 4看出，标准动应力强度因子随θ的增大而增大；θ一定时标准动应力强度因子随aω的增大而减小。对相同入射频率入射角越大。较大入射角可抑制标准动应力强度因子峰值出现，表明材料的标准动应力强度因子可通过入射角控制。适当调节载荷入射角可抑制材料的性质变化及裂纹扩展。

（4）由图2～图4知，标准动应力强度因子将随波数 aω的增加而减小。因此工程中通过调整入射波频率可降低裂纹尖端集中，通过改变入射波频率实现应力场改变。

（5）由计算结果知，标准动应力强度因子不仅与裂纹长度、裂纹至界面距离、入射波频率及入射角有关，亦与材料性质有关。

［1］Sih G C，Song Z F.Magnetic and electric poling effects associated with crack growth in BaTiO3－CoFe2O4 composite［J］.Theoretical and Applied Fracture Mechanics，2003，39（3）：209－227.

［2］Shen SP，Kuang Z B.Wave scattering from an interface crack in laminated anisotropic media［J］.Mechanics Research Communication，1998，25（5）：509－517.

［3］Zhou Z G，Shen SP.Scattering of harmonic elastic waves by a plane interface crack with linear adhesive tip in a layered half space［J］.Acta Mechanica Solide Sinica，1994，7（2）：105－113.

［4］Ueda S.Diffraction of antiplane shear wave in a piezoelectric laminate with a vertical crack［J］.European Journal of Mechanics A／Solids，2003，22（3）：413－422.

［5］Ma Lin，Nie Wu，Wu Linzhi，et al.Scattering of antiplane stress wave by a crack in a nonhomogeneous orthotropic medium［J］.Composite Structures，2007，79（2）：174－179.

［6］杨娟，李星.功能梯度压电压磁材料中裂纹对 SH波的散射［J］.应用力学学报，2008，25（2）：279－283.YANG Juan，LI Xing.Scattering of SH wave on crack in functionally graded magnetoelectroelastic materials［J］.Chinese Journal of Applying Mechanics，2008，25（2）：279－283.

［7］杨娟，李星.功能梯度压电带拼接半无限大压电材料中裂纹对 SH波 散射的问题［J］.力学季刊，2010，31（4）：570－577.YANG Juan，LI Xing.Scattering of the SH wave on cracks in functionally graded piezoelectric strip bonded to a semiInfinite homogeneous piezoelectric［J］.Chinese Quarterly of Mechanics，2010，31（4）：570－577.

［8］杨娟，李星.SH波对功能梯度压电层－功能梯度半空间中裂纹的散射［J］.西北师范大学学报（自然科学版），2013，49（6）：41－46.YANG Juan，LI Xing.Scattering of the SH wave on crack in functionally graded piezoelectric striphalf functionally graded space［J］.Journal of Northwest Normal University，2013，49（6）：41－46.

［9］LIXing，Liu Junqiao.Scattering of the SH wave from a crack in a piezoelectric substrate bonded to a halfspace of functionally graded materials［J］.Acta Mechanica，2009，208（3／4）：299－308.

［10］Bi X S，Chen J，Chen X L.Moving crack for functionally grated material in an infinite length strip under antiplane shear［J］.Theoretical and Applied Fracture Mechanics，2003，39（1）：89－97.

附录