少齿差行星减速器振动特性仿真与实验研究

石 珍，王家序，肖 科，李俊阳，官 浩

（重庆大学 机械传动国家重点实验室，重庆 400030）

空间传动件因运行环境复杂恶劣，其使用可靠性及在轨寿命已成影响航天器在轨时间长短关键因素［1］。为适应航天器发展、满足其性能需求，新型少齿差行星齿轮传动件即滤波减速器应运而生［2］。少齿差内啮合行星齿轮传动形式具有传动比范围大、传动效率高、体积小、结构紧凑等特点，而齿轮传动的振动特性成关注重点［3－5］。影响齿轮啮合传动因素较多，如齿轮刚度，齿侧间隙等非线性因素，纯刚性分析方式往往忽略非线性因素干扰导致分析不准确。基于多体动力学理论及迟滞接触动力学方法［6－8］，采用刚柔耦合齿轮三维接触动力学模型的分析方法得到广泛应用［9－10］。而齿轮啮合过程中受到包括啮合刚度激励、误差激励、啮合冲击激励等轮齿啮合内部动态激励影响，计算齿轮装置固有频率及振型，综合考虑内外部激励成研究齿轮装置振动特性关键［11－12］。

本文以新型少齿差行星齿轮传动件为研究对象，考虑齿轮时变啮合刚度、轮齿变形等因素影响，建立刚柔耦合三维动力学模型，利用多体动力学相关理论，以振动加速度为表征方式对减速器加载不同转速、不同形式激励。用三维仿真与实验测试结合测定其多种工况振动响应频谱，为进一步改善新型少齿差行星齿轮传动件结构、性能提供依据。

1 减速器传动原理

少齿差行星减速器装配结构见图1，主要由偏心轴1、固定齿轮3、双联齿轮（外齿轮2、4一体化结构）及输出齿轮5组成。工作原理为：偏心轴1两端支持轴承几何中心与固定齿轮3中心重合，且偏心轴1偏心外圆中心与固定齿轮3中心存在一定偏心；当偏心轴1绕其几何中心转动时，迫使双联齿轮既绕自身几何中心自转又绕固定齿轮3几何中心公转；利用外齿轮2与固定齿轮3及外齿轮4与输出齿轮5的两对少齿差内啮合实现大减速比。行星减速器相关齿轮参数见表1。

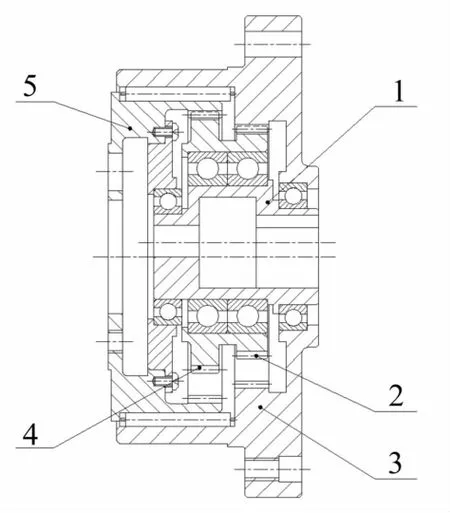
图1 行星减速器结构图Fig.1 Structural diagram of the planetary reducer

表1 行星减速器齿轮参数Tab.1 Gear parameters of the planetary reducer

2 动力学分析

2.1 齿轮系统非线性动力学

在齿轮系统非线性动力学基础上据其运动方程建立齿轮系统非线性扭转振动模型见图2。

图2 齿轮啮合动力学模型Fig.2 Dynamic model of gear mesh

据牛顿定律得齿轮系统非线性动力学模型为

式中：Ip，θg，Rp，Tp分别为主动轮转动惯量、扭转振动位移、基圆半径、外力矩；Ig，θg，Rg，Tg分别为被动轮转动惯量、扭转振动位移、基圆半径、外力矩；K（t）为齿轮时变啮合刚度；e（t）为齿轮传动误差；C为齿轮啮合阻尼；f（θ）为有齿侧间隙时齿轮啮合力对应的非线性函数。

2.2 刚柔耦合多体动力学

为求解耦合虚拟样机模型振动特性，需先求解柔性体模态，用 CraigBampton模态综合法据 CraigBampton模态综合理论用模态展开法建立模态矩阵为

3.1 虚拟样机模型建立

用Solidworks软件建立三维减速器装配体模型，导入Virtual.Lab软件中用Motion功能模块进行多体动力学分析［13－14］。在Motion中定义固定齿轮与大地固定连接特性，对其它各部件间定义正确的相对运动关系并施加约束，见表2。通过在Revolute Joint 3上添加RSDA力实现负载力矩加载，添加力矩值为80 N·m，在Revolute Joint 1上添加运动驱动Joint Position Driver 1，通过在Joint Position Driver 1上改变转速大小实现不同工况。据减速器实际工况计算值获得虚拟样机中模拟输入轴承的Spherical Bushing1球轴承刚度为9.73×107N／m，阻尼为 2.21×104kg／s；模拟转臂轴承的Spherical Bushing2球轴承刚度为1.33×108N／m，阻尼为2.11×104kg／s；模拟输出轴承的 Spherical Bushing3球轴承刚度为8.47×107N／m，阻尼为2.31×104kg／s。

通过定义建立刚性减速器齿轮系统非线性振动虚拟样机模型见图3（a）。采用自由网格划分方法，选四面体单元在满足分析要求及网格质量控制条件下对固定齿轮进行柔性化，网格划分得64 336个单元，形成耦

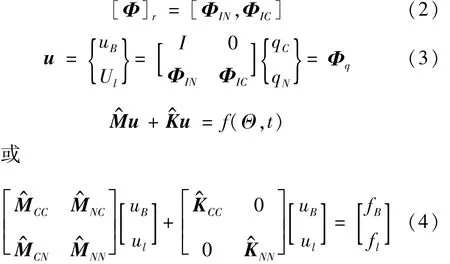
式中：ΦIN为主模态矩阵；ΦIC为约束模态矩阵；I，0分别为单位阵、零矩阵；M＾，K＾分别为转换后与新坐标对应的广义质量阵、刚度阵；fl，fB分别为固有模态力、约束模态力；f（Θ，t）为固有模态力、约束模态力函数；Θ为多体运动系统状态变量。

子宫切口憩室在妇产科存在有极高的发生率,对产妇产后健康造成较为严重影响,促使其生活质量持续下滑。手术治疗已成为该症最为主要的临床处理方式。

将模态矩阵Φ进行正则化转换后代回刚柔耦合运动系统建立Lagrange方程，采用BDF算法可获得耦合运动系统解。

3 虚拟样机模型建立与验证

合模型见图3（b）。

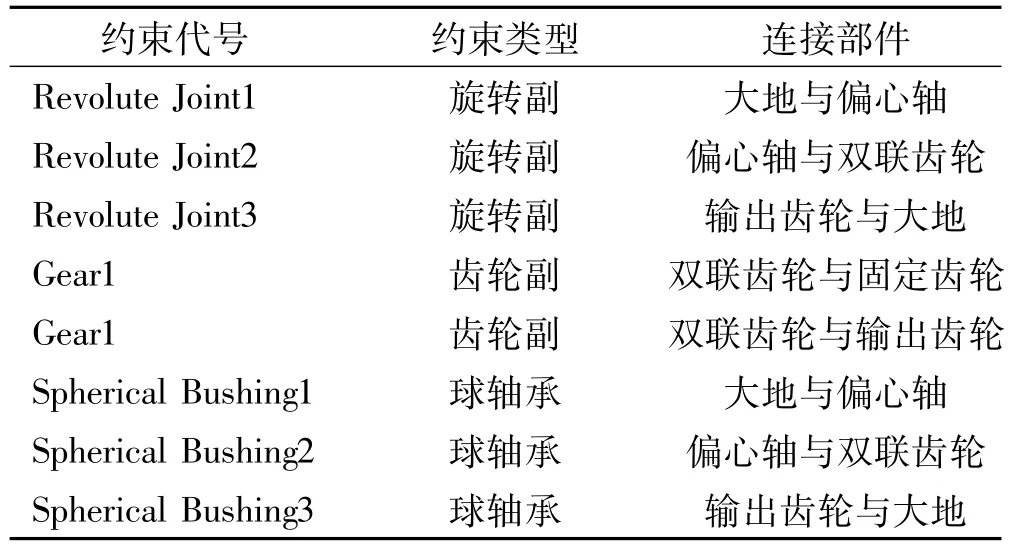
表2 各构件间约束关系Tab.2 Constraint relation between various components

图3 虚拟样机模型Fig.3 Virtual prototype model

3.2 虚拟样机模型验证方法

检验与判断虚拟样机模型与仿真结果准确性方法有将仿真数据与理论值比较或与实际模型实验数据比较等，比较数据应在保证实际模型与仿真虚拟样机模型相同条件下获得［15－16］。本文用动态关联法对虚拟样机模型进行验证。动态关联法包括THEIL不等式法、灰色关联度法等为定性的模型评价方法，可通过计算2个序列误差给出度量2个时间序列一致性程度性能指标。THEIL不等式系数对单输出时间序列定义为

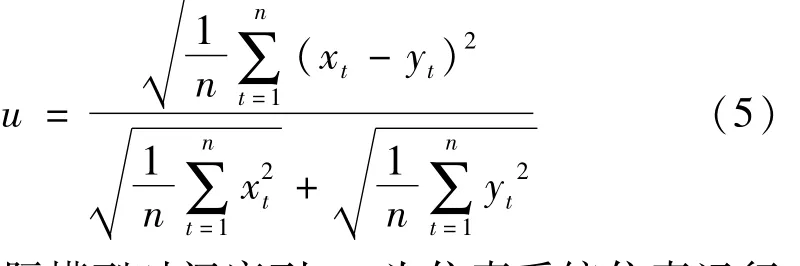
式中：xt为实际模型时间序列；yt为仿真系统仿真运行时间序列。

xt与yt的灰色关联系数为

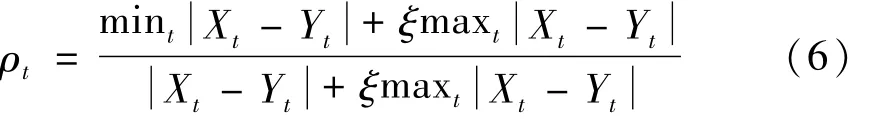
式中：ξ∈（0，1）为分辨系数，ξ根据模型具体情况取值，一般取值区间［0，1］或［0，0.5］。对取定的 ξ，ρt越大，xt与yt的关联程度越大。

定义灰色关联度为

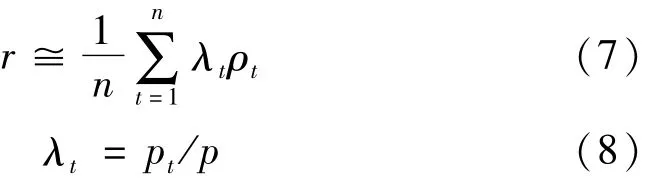
式中：pt为断面评价因子t的超标倍数当取定分辨系数ξ较小时，所得r较大（r≥0.5），则认为仿真输出与参考输出相关性较强。

3.3 虚拟样机模型验证

对虚拟样机模型中旋转副Revolute Joint1施加2 000 r／min恒定转速，据减速器理论传动比i＝－80，计算得输出齿轮理论转速为－25 r／min。图4为输出齿轮仿真转速曲线。在仿真结果数据中随机选10个值作为仿真时间序列并与实测参数理论计算恒定值比较，对应关系见表3。据表3数据用THEIL不等式计算得系数u≈0，由此减速器虚拟样机模型的准确性得以验证。

表3 理论与仿真结果时间序列对照Tab.3 Comparison of time sequence of theory and simulation results

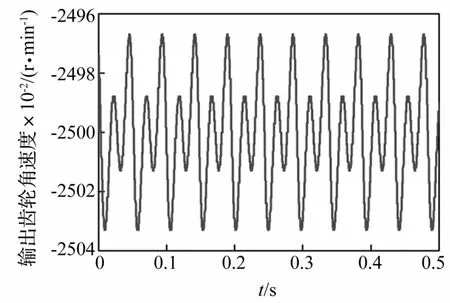
图4 输出齿轮的转速Fig.4 Rotate speed of the output gear

4 减速器振动特性仿真

为研究减速器不同转速条件的振动特性，仿真模型不仅考虑齿轮时变啮合刚度、轮齿变形，且考虑偏心轴弯曲变形及不平衡惯性力等影响。设仿真速度为300 r／min、600 r／min、1200 r／min、2000 r／min，仿真时间为0.5 s，仿真步长 1×10－4s，用 BDF算法，仿真结果见表4、图5～图10。图5为不同转速的减速器固定齿轮应力。由图5可知，随转速的增加固定齿轮最大等效应力先保持不变后稍微增加。仿真结果表明转速对减速器部件应力有一定影响，但不大。

表4 啮合力仿真值与理论计算值对比Tab.4 Meshing force value comparative of simulation and theoretical calculation

图6为减速器在转速1 200 r／min时输出齿轮与双联齿轮X、Y两方向啮合力，表4为啮合力仿真值与理论值对比。由图6看出，啮合齿轮啮合力在静态力左右上下波动，主要为减速器在动态运动过程中受偏心力、不平衡惯性力、变啮合刚度、轮齿变形影响，使啮合力上下波动。由表4知，仿真值与理论值误差较小，仿真具有一定可靠性。

图5 不同转速下固定齿轮最大等效应力Fig.5 Fixed gear max equivalent stress at different rotate speed

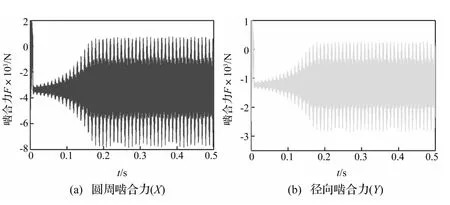
图6 1 200 r／min时输出齿轮与双联齿轮啮合力Fig.6 Meshing force of output gear and double gear at 1 200 r／min

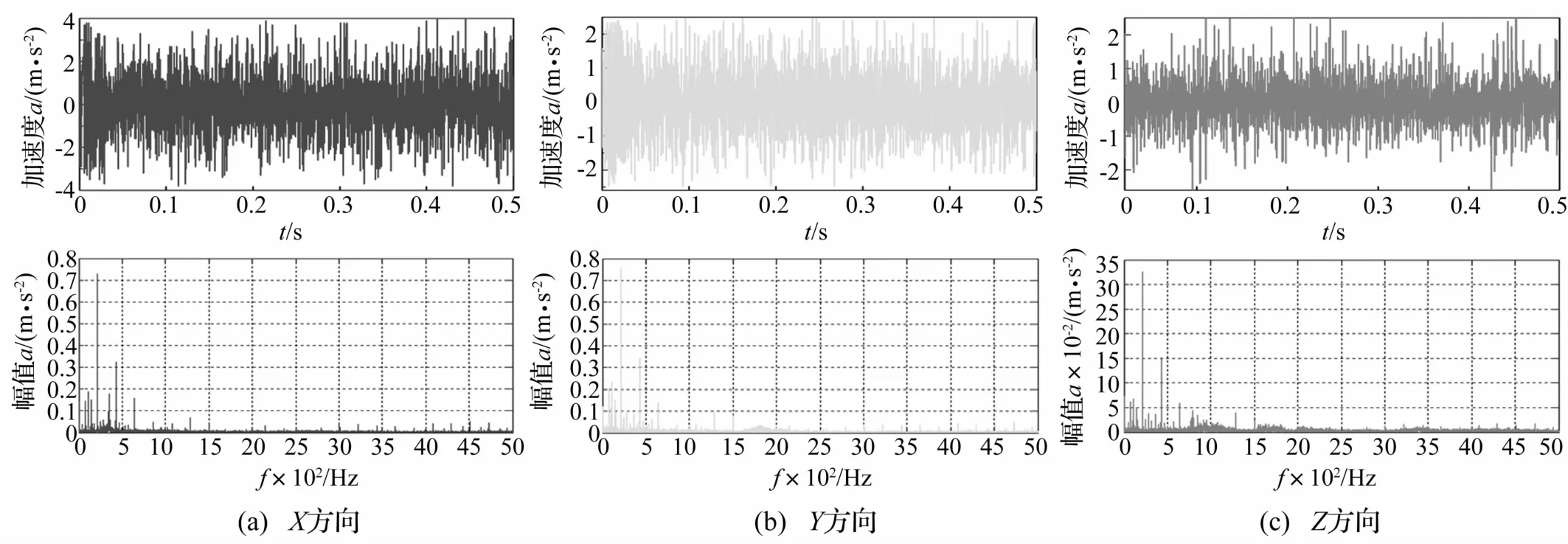
图7 600 r／min时节点32 023各向振动加速度位移及频谱Fig.7 Vibration acceleration displacement and frequency spectrum of node 32 023 at 600 r／min

对固定齿轮柔性化后选节点32 023分析振动特性。图7为600 r／min固定齿轮节点32 023的振动加速度位移及频谱，。由图7看出，径向X、Y向振动加速度位移、频率幅值大于轴向Z向振动加速度，仿真结果表明减速器整体径向振动较轴向大。

图8、图 9、图 10分别为转速 300 r／min、1 200 r／min、2 000 r／min时节点32 023 X向振动加速度位移及频谱。仿真响应结果在某些时间点出现较大加速度响应幅值，表明减速器运动过程中存在少量冲击性幅值，主要因偏心轴偏心运动对轮齿啮合冲击及滚珠冲击。由图7～图10知，随转速的提高，减速器部件振动加速度位移及频谱幅值增大即振动加大，造成冲击幅值越多。因此，转速提高偏心轴偏心运动越明显，偏心轴对轮齿啮合冲击与滚珠冲击加大，减速器振动加剧，冲击幅值增大。

图8 300 r／min节点32 023 X向振动加速度位移及频谱Fig.8 X－direction vibration acceleration displacement and frequency spectrum of node 32 023 at 300 r／min

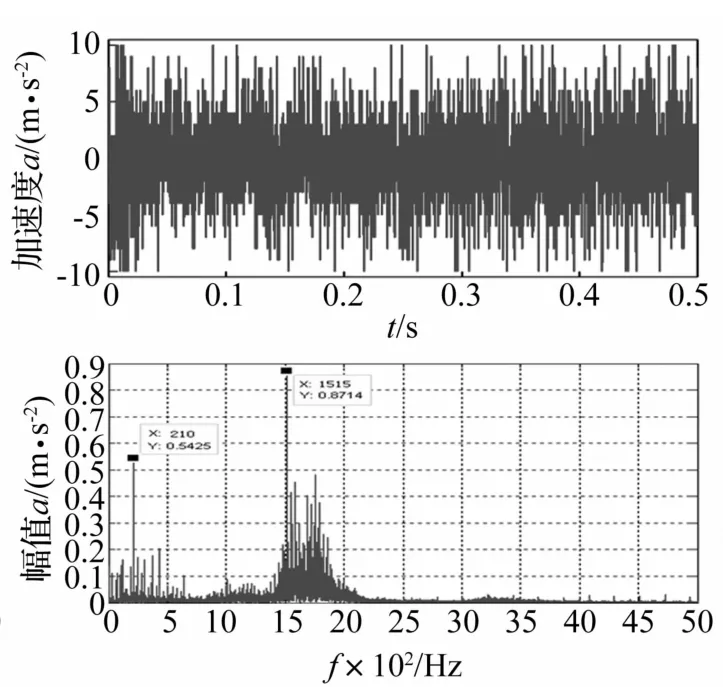
图9 1 200 r／min节点32 023 X向振动加速度位移及频谱Fig.9 X－direction vibration acceleration displacement and frequency spectrum of node 32 023 at 1 200 r／min

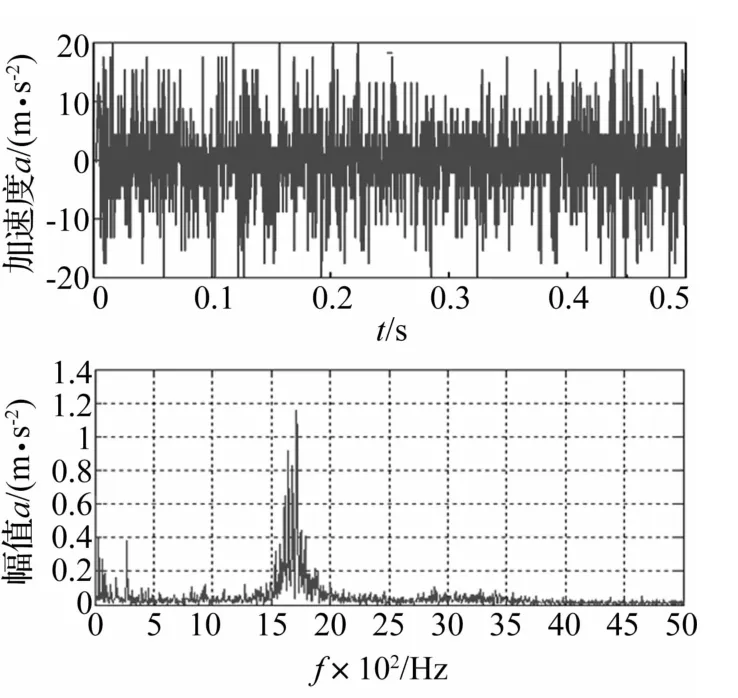
图10 2 000 r／min节点32 023 X向振动加速度位移及频谱Fig.10 X－direction vibration acceleration displacement and frequency spectrum of node 32 023 at 2 000 r／min

5 减速器振动测试

5.1 振动测试方法与测试设备

据国标GB8543－1987规定对减速器固定齿轮表面振动进行测试。齿轮装置振动响应测试主要用加速度传感器测量加速度振动信号，经放大器后进入智能信号采集处理分析仪，对采集数据记录及分析。本次试验用北京东方振动和噪声技术研究所的INV3018C型24位智能信号采集处理分析仪、INV9832 ICP型三向加速度传感器、INV1841A型电荷调理仪等设备及DASP V10专业版信号处理、分析软件。行星减速器振动测试见图11。

图11 行星减速器振动试验台Fig.11 Vibration test stand for the planetary reduce

5.2 减速器齿轮装置测点布置

在减速器固定齿轮上布置8个测量点，测点布置如图12所示，测点1、3、5、7均布在固定齿轮圆周面测量减速器三个方向的振动。测点2、4、6、8均布在固定齿轮大端面测量减速器三个方向的振动。

5.3 减速器振动测试结果

减速器测试工况输入转速为 300 r／min、600 r／min、1 200 r／min、2 000 r／min，测试 8点三方向振动加速度，并以平均值为测试值。转速600 r／min减速器振动加速度见图 13，转速为 300 r／min、1 200 r／min、2 000 r／min时减速器X方向振动加速度分别见图14、图15、图16，不同转速的减速器振动加速度仿真与实验值均方根值即有效值见表5。

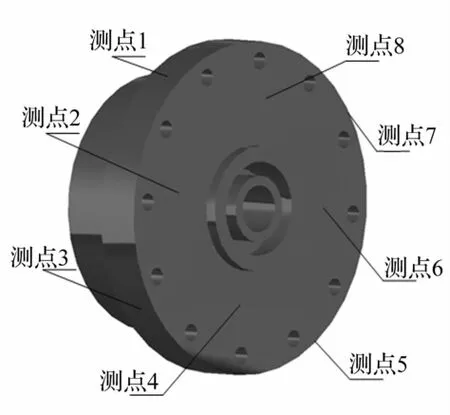
图12 测点布置Fig.12 Arrangement of measuring points

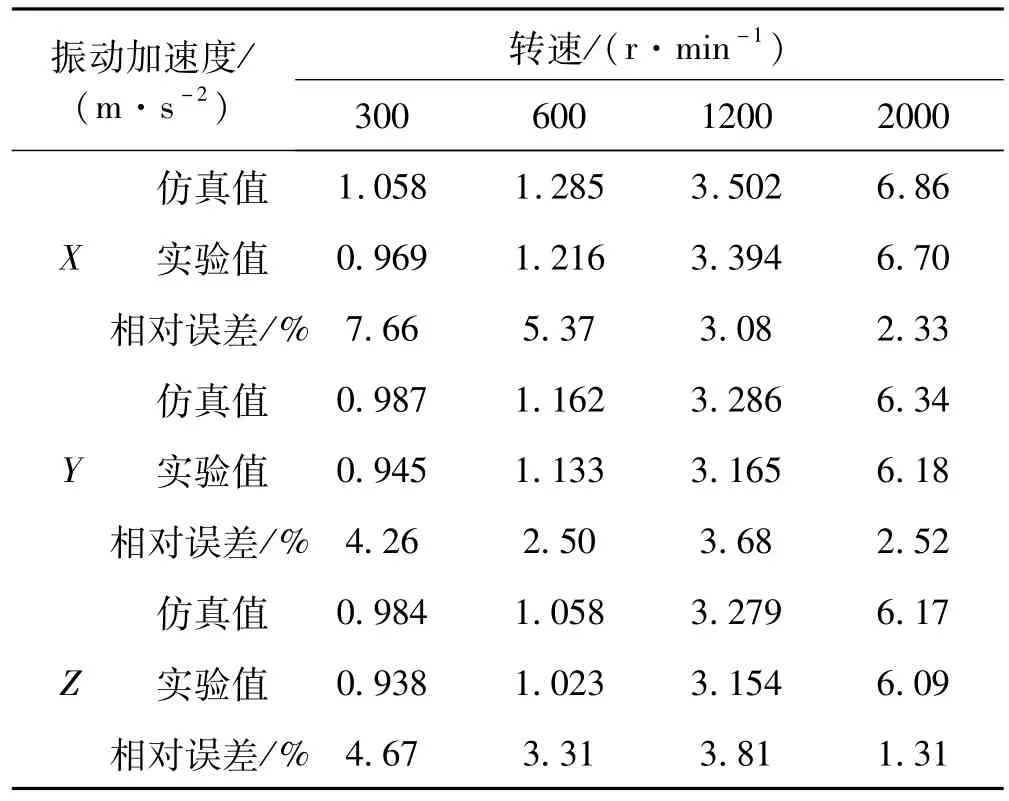
表5 不同转速仿真与实验有效值对比Tab.5 Comparative analysis of simulation and experimental RMS under different rotational speeds

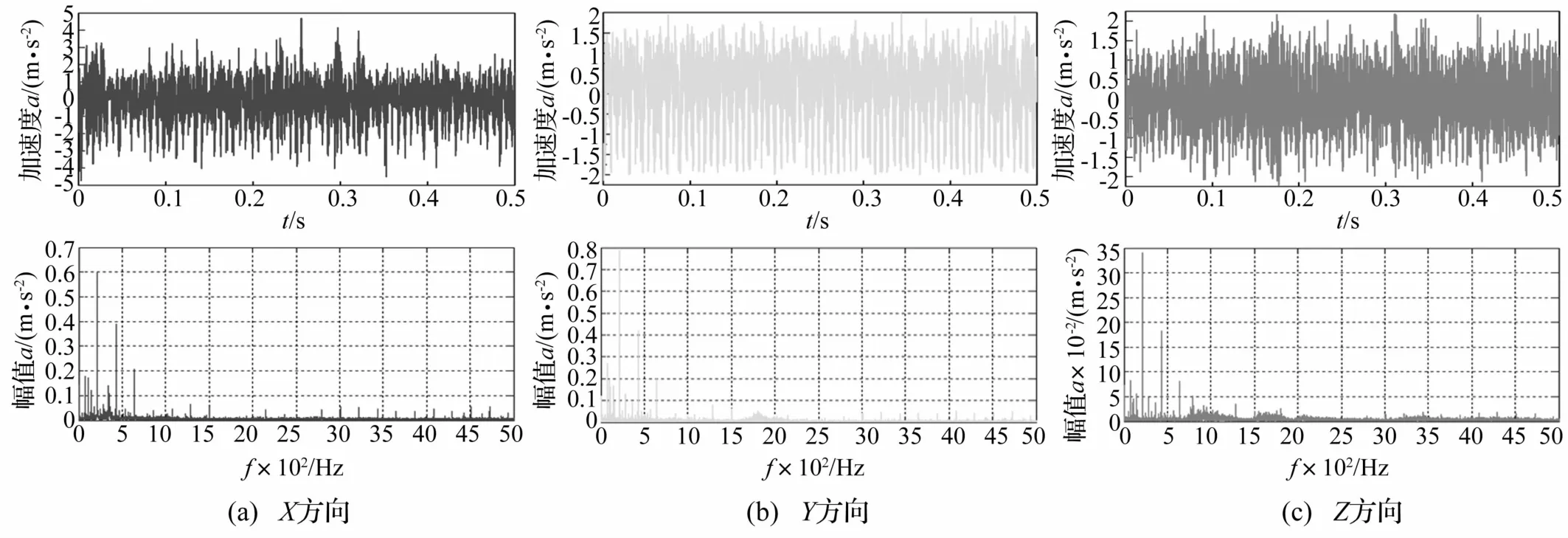
图13 600 r／min时测试振动加速度位移及频谱Fig.13 Test vibration acceleration displacement and frequency spectrum at 600 r／min

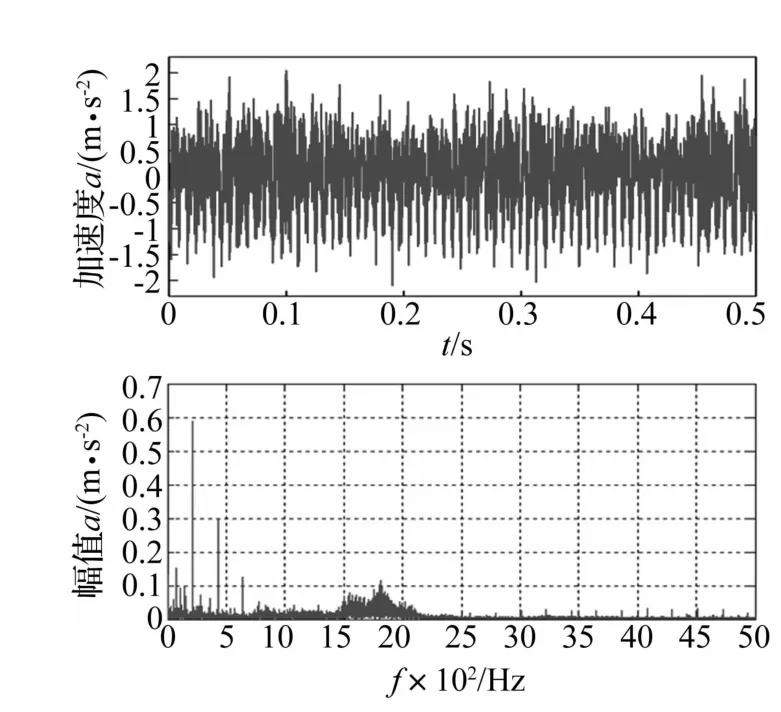
图14 300 r／min时X方向振动加速度位移及频谱Fig.14 X－direction test vibration acceleration displacement and frequency spectrum at 300 r／min

图15 1 200 r／min X方向振动加速度位移及频谱Fig.15 X－direction test vibration acceleration displacement and frequency spectrum at 1 200 r／min

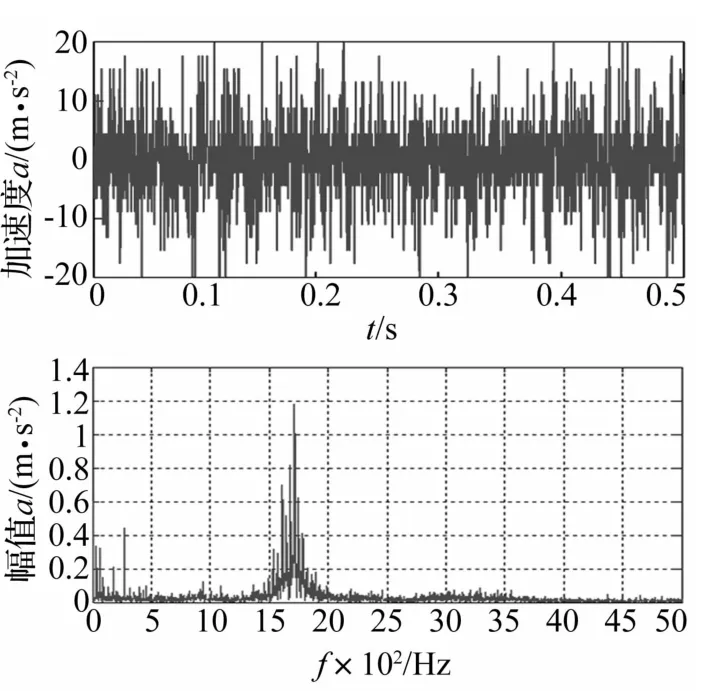
图16 2 000 r／min X方向振动加速度位移及频谱Fig.16 X－direction test vibration acceleration displacement and frequency spectrum at 2 000 r／min

由图9、图15看出，仿真加速度峰值频率出现在210 Hz及1 515 Hz，与实验加速器出现的峰值频率214.8 Hz及1 520 Hz较接近，且对应振动加速度峰值0.542 5、0.871 4 m／s2及 0.592 5、0.737 3 m／s2也较相近。表5中不同工况仿真与振动加速度有效值最大误差7.66%，总体误差较小。由图13～图16及表5看出，减速器固定齿轮实验所测振动加速度与动力学仿真结果吻合度较高，达到预期研究效果。

6 结 论

（1）建立包括双联齿轮、输出齿轮、固定齿轮、偏心轴等组成的整个少齿差行星减速器多体动力学非线性振动模型，利用动态关联法对动力学虚拟样机模型进行验证。

（2）考虑齿轮时变啮合刚度、轮齿变形、偏心轴弯曲变形及不平衡惯性力情况计算减速器不同转速的等效应力及动态响应。

（3）对减速器振动加速度进行测试。减速器动力学仿真分析及测试结果表明，动态仿真分析结果与测试值基本吻合。转速对减速器部件应力影响很小，对减速器振动影响较大，且减速器整体径向振动较轴向大。随转速提高，偏心轴偏心运动越明显，偏心轴对轮齿啮合冲击、滚珠冲击加大，减速器振动加剧，冲击幅值增大。

［1］肖科，王家序，刘文吉，等.新型高性能空间摩擦副设计［J］.中国机械工程，2008，19（22）：2650－2653.XIAO Ke，WANG Jiaxu，LIU Wenji，et al.Design of new type high performance space friction pairs［J］.Chinese Journal of Mechanical Engineering，2008，19（22）：2650－2653.

［2］王家序，田凡，肖科.固体润滑精密滤波驱动驱动装置［P］.中国：ZL200710135602.8，2007－09－26.

［3］Ambarisha V K，Parker RG.Nonlinear dynamics of planetary gears using analytical and finite element models［J］.Journal of Sound and Vibration，2007，302（3）：577－595.

［4］Li S T.Contact problem and numeric method of a planetary drive with small teeth number difference［J］.Mech.Mach.Theory，2008，43（9）：1065－1086.

［5］Daisuke S K，Shigeru H C，Jin H C.Dynamic analysis of contacting spur gear pair for fast system simulation［J］.Trans Tech Publications，2006，110：151－162.

［6］Eberhard P，Schiehlen W.Computational dynamics of multibody systems：history，formalisms，and applications［J］.Journal of Computational and Nonlinear Dynamics，2006，1：1－12.

［7］Ziegler P，Eberhard P，Schweizer B.Simulation of impacts in geartrains using different approaches［J］.Archive of Applied Mechanics，Published Online，2006，76（9／10）：537－548.

［8］Tamer M W，Noor A K.Computational strategies for flexible multibody systems［J］.Appl.Mech.Rev，2003，6：553－613.

［9］朴明伟，方吉，赵钦旭，等.基于刚柔耦合仿真的集装箱车体振动疲劳分析［J］.振动与冲击，2009，28（3）：1－6.PIAO Mingwei，FANG Ji，ZHAO Qinxu，et al.Vibration fatigue analysis of a container flatcar based on rigidflexible coupling simulation［J］.Journal of Vibration and Shock，2009，28（3）：1－6.

［10］姚廷强，迟毅林，黄亚宇，等.刚柔耦合齿轮三维接触动力学建模与振动分析［J］.振动与冲击，2009，28（2）：167－171.YAO Tingqiang，CHI Yilin，HUANGYayu，et al.Contact dynamics modeling and simulation on rigidflexible gear pair［J］.Journal of Vibration and Shock，2009，28（2）：167－171.

［11］ Ebrahimi S，Eberhard P.Rigidelastic modeling of gear wheels in multibody systems［J］. Multibody System Dynamics，2006，16：55－71.

［12］Guo Y，Parker RG.Dynamic modeling and analysis of a spur planetary gear involving tooth wedging and bearing clearance nonlinearity［J］.European Journal of MechanicsA／Solids，2010，29（6）：1022－1033.

［13］邓辉咏，刘海平，徐元村.基于Virtual Lab的某型减速器建模及仿真［J］.军械工程学院学报，2007，19（1）：51－54.DENG Huiyong，LIU Haiping，XU Yuancun.Modeling and simulation of a reducer based on Virtual.Lab［J］.Journal of Ordnance Engineering College，2007，19（1）：51－54.

［14］Mauer L.Force element 225 gear wheel internal report［C］.Intec GmbH，Wessling，Germany，2005.

［15］ Hippmann G.An algorithm for compliant contact between complexly shaped bodies［J］.Multibody System Dynamics，2004，12：345－362.

［16］段福海，胡青春，谢存禧.钢／塑齿轮组合行星传动的振动特性［J］.机械工程学报，2010，46（1）：62－67.DUAN Fuhai， HU Qingchun， XIE Cunxi. Dynamic behavior for planetary geared system with plastic gear［J］.Journal of Mechanical Engineering，2010，46（1）：62－67.