智能作动器Preisach迟滞参数辨识及补偿研究

王萍萍，刘 磊，栾晓娜

（1.哈尔滨工业大学 航天学院，哈尔滨 150001；2.大连理工大学 航空航天学院，辽宁 大连 116024）

智能作动器广泛用于微纳米技术领域，但其迟滞非线性效应影响作动器精度，而迟滞非线性效应造成的误差可达位移的10%～15%［1］。为提高作动器精度，需研究智能作动器迟滞非线性辨识及补偿［2］。

迟滞效应物理特性较复杂，可通过基于现象的数学模型描述，尤其 Preisach模型［3－4］。经典 Preisach迟滞非线性只依赖输入信号路径，与信号频率无关，而Preisach具有全局记忆性［5］，即过去、当前时刻输入共同决定将来某时刻输出。为辨识Preisach模型，Henze等［6］通过假设Preisach模型μ分布函数利用数据点进行参数辨识，但通常较难提前获得某压电作动器的μ分布函数；Song等［7］对输入信号进行微分求解Preisach密度函数，但易受测量噪声影响。本文用最小二乘与奇异值分解方法辨识Preisach模型参数。噪声及扰动也会产生小的奇异值，需进行截断以减小误差。但若输入信号不满足持续激励（PE）条件［8－9］，也易造成较大辨识误差。因此需采用具有变幅值的输入信号进行参数辨识，以满足持续激励条件，提高辨识精度。为验证辨识结果，本文设计Preisach逆模型前馈补偿迟滞非线性，利用压电平台实验验证迟滞辨识、补偿方法的有效性。

1 Preisach迟滞非线性模型

1.1 Preisach迟滞非线性模型

经典Preisach迟滞非线性模型为迟滞算子与相应密度函数 μ的二重积分［2］，即

式中：u（t）为输入电压；μ（α，β）为无量纲密度函数；f（t）为作动器输出；rαβ为迟滞算子也称继电器算子。

式（1）不含动力学项，故对Preisach迟滞参数辨识不同于一般动力学系统。

1.2 Preisach迟滞非线性模型离散化

对Preisach迟滞非线性模型参数辨识时主要目标即辨识密度函数μ。本文对Preisach平面进行离散化，并设单元具有均匀密度μij，将二重积分转化为求和，即

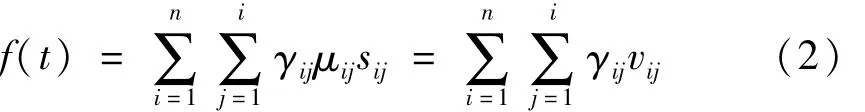
式中：n为离散水平；sij为单元格（i，j）面积（已知）；γij为单元格（i，j）继电器输出，可指定为特殊值，如对压电陶瓷作动器γij可指定0或1，即vij＝μijsij，故只要辨出 vij即可求出 μij。

对式（2）在时间区间t1＜t＜tm内采样，故存在时间序列t1＜t2＜…＜ti＜…＜tN，对迟滞离散方程N个采样，得线性矩阵方程为

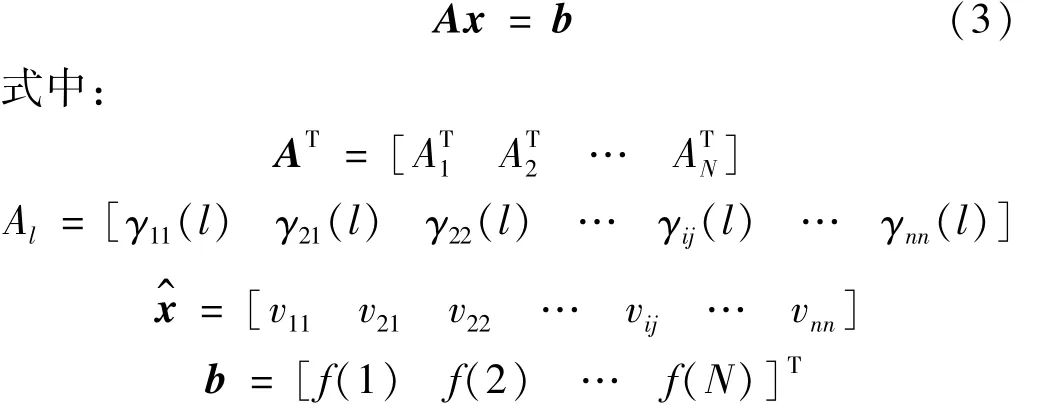
对Preisach迟滞非线性辨识转化为对式（3）的求解。通常式（3）的维数、条件数较高，如对n＝50的离散化，矩阵A的维数为1 275，采用一般输入信号、一般求解方法较难获得精确解。本文目的即采用恰当的谐波输入信号，构造式（3），对矩阵ATA进行奇异值分解，辨识离散化密度函数μij，并用逆模型前馈补偿迟滞效应验证辨识方法的正确性。

2 奇异值分解法辨识Preisach模型参数

2.1 Preisach模型参数辨识

用于谐波信号辨识Preisach迟滞模型参数不同于非迟滞动力学，频率丰富并非能提高迟滞效应辨识精度，主要因Preisach模型速率无关性，即单独改变输入信号频率不能改变Preisach模型输出特性。密度函数为恒定值4，在0.5 s时输入信号频率增加为2倍，迟滞回路仍保持不变，见图1。

相反，充分幅值可激发更多记忆曲线，Presach模型中不同状态点被激发，可满足持续激励（PE）条件、提高Preisach迟滞模型参数辨识精度，变幅值输入谐波信号及Preisach回路见图2。由图2看出，变幅值输入信号生成更多迟滞回路，采样时可产生更多线性独立方程，提高矩阵A的秩，增加参数辨识精度。

2.2 满足持续激励条件的最小二乘解

对一般非迟滞系统，参数辨识均会构造充分频率的输入信号，尽量激发系统模态满足持续激励条件，即det（ATA）≠0，此时方程存在唯一解［8］为

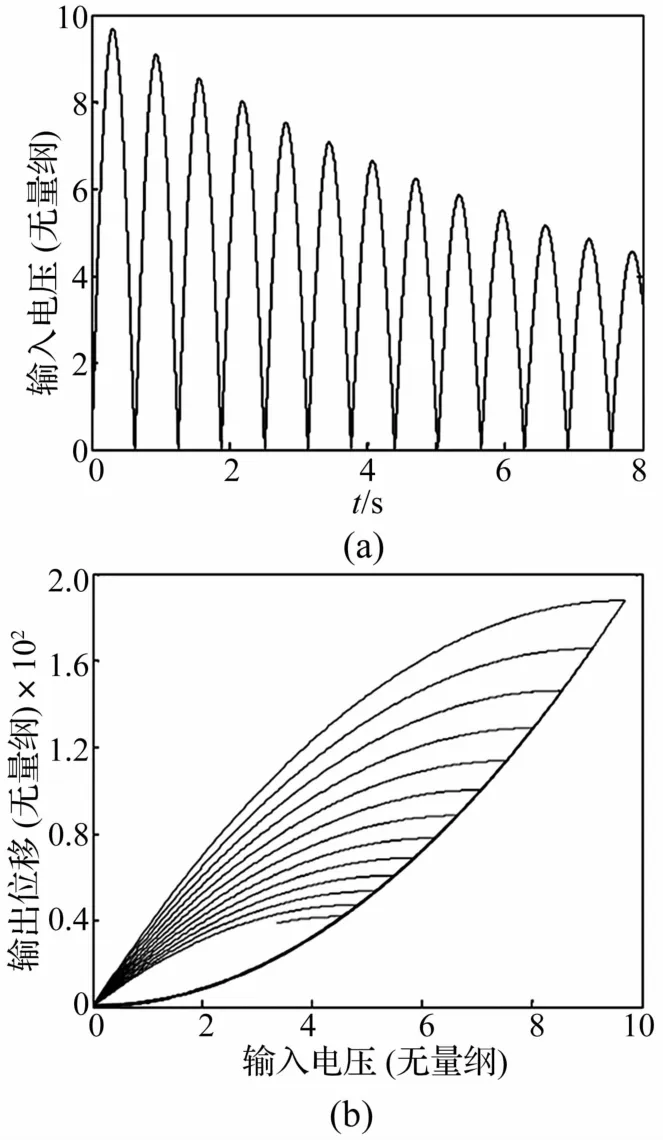
图2 变幅值输入信号及Preisach回路Fig.2 Amplitudevarying input and its Preisach loop

但对Preisach迟滞非线性，充分频率无助于提高辨识精度，且因矩阵A维数高、存在系统噪声，接近零的奇异值会增加误差。为提高精度，需对接近零的奇异值截断。单纯采用一般辨识方法式（4）不易获得参数精确值。

2.3 奇异值分解参数辨识

本文采用最小二乘法辨识迟滞模型。为提高辨识精度，对矩阵ATA奇异值进行分解［10］，即

式中：U＝［u1，u2，…，un］；V＝［v1，v2，…，vn］；∑ ＝diag（σ1，σ2，…，σn）；σ1≥σ2≥…≥σn≥0；U，V为么矩阵，满足 UUT＝UTU＝I，VVT＝VTV＝I，I为单位阵。

设矩阵 ATA的秩为 k，存在 σk＋1，σk＋2，…，σn＝0，对ATA进行分解，即

求伪逆时，奇异值截断既要考虑截断误差，也要考虑测量噪声影响。噪声可能会产生非常小奇异值，影响矩阵良定性。可用条件数衡量矩阵的良定性，ATA条件数 k（ATA）为

式中：σ1为最大奇异值；σk为最小非零奇异值；k（ATA）为最大最小奇异值比例。若条件数太大，ATA属于非良定矩阵。

3 Preisach迟滞非线性逆模型补偿

Preisach迟滞为具有全局记性效应的非线性，无动力学环节。本文对迟滞补偿时采用具有记忆效应的逆模型法补偿［11］，此为前馈补偿算法，依赖于辨识精度。一旦获得Preisach迟滞模型即可据过去及当前输入信号决定输出信号。为验证辨识精度，逆模型补偿时不用位移测量，直接据辨识Preisach模型及参考信号求解控制电压u（k），补偿算法见算法1，其中Ψ为辨识的Preisach迟滞模型。在该算法中，k时刻参考位移为fr（k），位移估计为＾f（k），控制电压u（k＋1）使（k＋1）跟踪 fr（k）。

压电作动器位移估计表达式为

式中：Ak为k时刻γij状态集为x的估计。

算法：Preisach逆模型补偿

式中：γ用于调节步长；umax为辨识的最大电压。

4 迟滞效应辨识及补偿方法实验验证

微纳米压电作动平台见图3，采用压电堆栈作动器及运动放大结构以获得更大位移，用电容传感器测量位移。压电设备安装于气浮平台，以减少环境振动、噪声影响。

图3 微纳米压电平台Fig.3 Micro／nano piezoelectric stage

4.1 迟滞效应辨识实验

在0～60 V电压区间用低频输入信号对迟滞非线性进行参数辨识。所用变幅值谐波输入信号见图4。由图4看出，电压信号频率为π／3 rad／s时，其幅值由1 V递增到60 V。

在变幅值谐波输入电压激励下压电位移输出见图5。由图5看出，位移发生漂移，“”点对应0 V电压，据Preisach模型擦除特性，输入电压回零时对应的位移应亦为零，仍发生的位移应作为漂移处理。

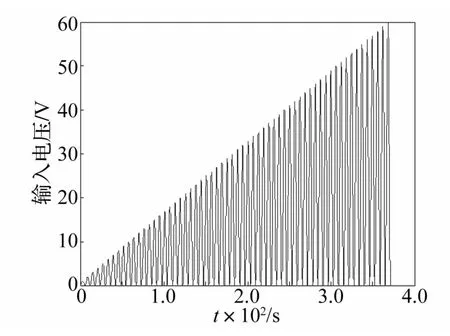
图4 变幅值输入谐波信号Fig.4 Input signals with variant amplitudes

图5 压电平台位移输出信号Fig.5 Displacement output of piezoelectric stage

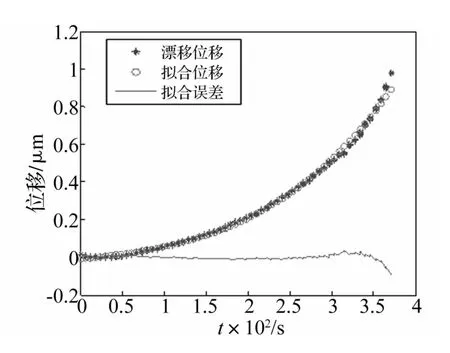
图6 曲线拟合法抑制漂移结果Fig.6 Drift suppression result using curve fitting

本文用多项式拟合法对特殊点拟合，给出曲线方程，再对其它点插值求解漂移值。拟合曲线表达式为

式中：fdrift为位移漂移量；t为时间。

据拟合曲线方程fdrift补偿位移漂移量，补偿结果见图6，补偿误差均方根为0.012μm。位移漂移补偿后的迟滞环（回路）见图7。由图7看出，曲线拟合迟滞环漂移已有效减小。

对补偿漂移后的迟滞环进行采样，设单元格（i，j）内点的γij一致，本文中单元格被激活时γij＝1，否则取0；且设离散化水平n＝60，对矩阵ATA进行奇异值分解，矩阵满秩，但条件数 k（ATA）＝3.32×1021，矩阵非良定，对小于最大奇异值0.000 01倍的奇异值进行截断，由式（9）所得μ的辨识结果见图8。由图8看出，密度函数μ均大于零。

图7 迟滞回路Fig.7 Hysteretic loops

图8 密度函数μ辨识结果Fig.8 Identified result of density functionμ

图9 模型逆补偿误差Fig.9 Error with model inversion compensation

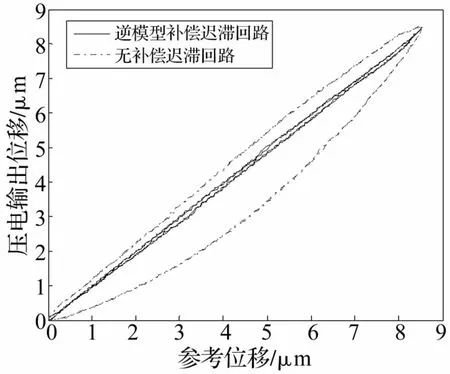
图10 逆补偿前后迟滞回路Fig.10 Hysteretic loop with and without compensation

4.2 逆模型迟滞补偿实验

本文采用逆模型迟滞补偿验证参数辨识的正确性，主要为因逆模型补偿对建模误差敏感；而逆模型前馈补偿也可在不用测量信号基础上补偿迟滞非线性，故应用前景较好。

据以上辨识结果，采用逆模型补偿算法，由于密度函数μ总大于零，故其逆函数总存在。式（13）中γ取0.04，umax＝60，用逆补偿后参考跟踪误差见图9。由图9看出，不用逆模型补偿时跟踪误差均方根为0.678 μm，而用逆模型补偿后误差均方根为0.071μm，减小89.5%。

参考信号与输出位移间迟滞回路见图10。由图10看出，逆模型补偿能有效减小迟滞效应及跟踪误差，表明Preisach建模及辨识的准确性。

5 结 论

（1）本文通过研究Preisach迟滞非线性辨识及补偿方法，构造变幅值谐波输入信号以满足持续激励条件；

（2）通过奇异值分解、截断小奇异值，用矩阵伪逆获得辨识的最小二乘解；

（3）用逆模型补偿不仅能验证参数辨识结果亦可补偿迟滞非线性，并通过压电平台实验验证本文方法的正确性。

［1］Ge P，Jouaneh M.Tracking control of a piezocermic actuator［J］.IEEE Trans.Contro Syst.Technol.，1996，13（8）：973－983.

［2］Leang K，Zou Q，Devasia S.Feedforward control of piezoactuators in atomic force microscope systems［J］.IEEE Control Syst.Magzine，2009，29（1）：70－82.

［3］党选举，梁卫，姜辉.基于改进Preisach模型的音圈电机复杂迟滞建模［J］.振动与冲击，2012，31（21）：156－162.DANG Xuanju，LIANG Wei，JIANG Hui.Complex hysteresis modeling for a voice coil motor based on improved preisach model［J］.Journal of Vibration and Shock，2012，31（21）：156－162.

［4］刘旺中，陈照波，侯守武，等.基于Preisach理论的形状记忆合金温度－位移迟滞仿真研究［J］.振动与冲击，2012，31（16）：83－87.LIU Wangzhong，CHEN Zhaobo，HOU Shouwu，et al.Simulation on modeling of temperaturedisplacement hysteresis in SMA based on preisach theory［J］.Journal of Vibration and Shock，2012，31（16）：83－87.

［5］Mayergozy I D.Mathematical modeling of hysteresis and their application［M］.Amsterdam：Elsevier，1991.

［6］Henze O，Rucker W M.Identification procedures of preisach model［J］.IEEE Trans.Magn.，2002，38（2）：833－836.

［7］Song G，Zhao J，Zhou X，et al.Tracking control of a piezoceramic actuator with hysteresis compensation using inverse Preisach model［J］.IEEE Trans.Magn.，2005，10（2）：198－209.

［8］Astrom K，Wittenmark B.Adaptive control［M］.New York：AddisonWesley；1994.

［9］Tan X，Baras J.Adaptive identification and control of hysteresis in smart materials［J］. IEEE Transactions Automatic Control，2005，50（6）：827－839.

［10］ Aster R，Borcher B，Thurber C.Function analysis and inverse problem［M］.Amsterdam：Elsevier，2005.

［11］刘磊.航天器主动隔振及精确定向控制技术研究［D］.哈尔滨：哈尔滨工业大学，2011.