双分裂导线间隔棒防舞数值模拟研究

崔 伟，严 波，杨晓辉，吕中宾

（1.重庆大学 工程力学系，重庆 400044；2.河南省电力公司 电力科学研究院，郑州 450052；3.上海交通大学 电气工程系，上海 200030）

输电线舞动产生的危害轻者闪络、跳闸，重者金具及绝缘子损坏、导线断股断线、杆塔螺栓松动脱落甚至倒塔，导致重大电网事故。因此，输电线路舞动及防治技术研究具有重要的理论及实际意义。

间隔棒具有绝缘性能与机械强度被用于导线或回路之间。其使各导线运动相互制约以达到抑制舞动目的［1］。已有关于间隔棒治理舞动的研究。Lilien等［2］系统介绍间隔棒在输电线路舞动防治中的发展、种类、布置方案等。Dyke等［3］在试验线路上安装D形人工覆冰模型，并在部分线路段安装间隔棒研究覆冰导线舞动及防舞技术，并取得一定研究成果，但缺乏理论认识。郭应龙等［1］基于以往研究介绍间隔棒的防舞设计方法。侯镭等［4］利用集中质量计算模型研究复合间隔棒芯棒直径、重量及抗弯刚度等参数对舞动影响，但所用模拟方法过于简化。有限元数值模拟方法已用于间隔棒防舞技术研究。Kim等［5］利用ANSYS有限元软件模拟研究间隔棒对三相单导线、双分裂导线的防舞效果，但模拟中将风载荷简化成正弦激励的处理方式与实际相差甚远。Fan等［6］利用有限元方法研究四分裂导线安装间隔棒的防舞效果，分析间隔棒沿档排布方式对防舞效果影响，数值模拟中将风载荷视为稳定载荷。而已有研究均未考虑实际风载荷的随机性。由于三相导线基本平行排列，数值模拟分析中若不考虑风荷载的空间分布及随机性，较难反映各相导线运动的差异性及间隔棒对各导线运动的约束作用。为此本文用数值方法生成考虑空间相关性的随机风场，利用ABAQUS有限元软件模拟研究间隔棒对双分裂导线舞动的防治效果，对间隔棒舞动防治技术及优化方案的进一步研究具有重要意义。

1 典型线路段及有限元建模

1.1 线路段及间隔棒布置

以两条分别用三角形、垂直排布方式的三相双分裂线路为研究对象，见图1。线路档距l均200 m，导线型号LGJ－400／50，导线物理参数见表1。每根子导线初始应力均66.2 MPa。设导线上覆冰形状为新月形，覆冰厚度12 mm，初始凝冰角为45°。

表1 导线LGJ－400／50物理参数Tab.1 Physical parameters of conductor LGJ－400／50

档内双分裂导线安装型号为FJQ－4053的3根子导线间隔棒，单个重2.71 kg，安装位置按输电线路设计规程［7］确定。3根子导线间隔棒左端距离分别为33.3 m、100 m、166.7 m。线路中安装的两根间隔棒长度据间距确定。对该两线路的模拟分析知其舞动为单半波模式，安装位置据文献［1］方法确定，布置于档距中间，两根间隔棒离导线两端距离均为0.425l，两间隔棒相距0.15l。间隔棒直径24 mm，弹性模量50 GPa。排布位置及方式见图2。

图2 线路段及间隔棒安装位置Fig.2 Installation location of interphase spacers in transmission lines

1.2 有限元模型

本文利用ABAQUS有限元软件模拟覆冰分裂导线舞动方法［8－9］。有限元模型中包括子导线及间隔棒，因此可考虑各子导线由尾流引起的不同气动载荷与实际更加接近。覆冰导线采用具有扭转自由度的索单元模拟，通过释放空间梁单元节点弯曲自由度保留扭转自由度，并将材料性质设为不可压缩模拟索单元。子导线间隔棒刚度较导线大，故可简化为圆形直杆用空间梁单元模拟。间隔棒亦用空间梁单元模拟。建立有限元模型时每根子导线划分600个具有扭转自由度的索单元，每根子导线间隔棒分为2个梁单元，每根间隔棒分为15个梁单元，以满足单元收敛性。采用无需迭代方法［10］确定分裂导线在自重作用下的初始形状。

1.3 覆冰导线与间隔棒上载荷

风作用于非对称截面覆冰导线的气动载荷为升力FL、阻力FD及扭矩M，计算式为

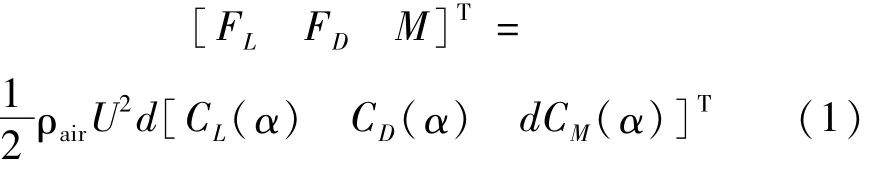
式中：ρair，U为空气密度、来流风速；d为导线直径；CL，CD，CM为升力系数、阻力系数及扭矩系数，随风攻角α变化，由风洞试验测得。

覆冰导线运动过程中其风攻角会不断变化，因此作用于导线上气动载荷亦不断变化。模拟覆冰导线舞动时可利用ABAQUS用户自定义单元子程序UEL施加气动载荷［9］。作用于间隔棒上风压荷载计算式［7］为

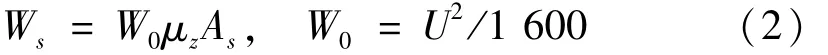
式中：W0为基准风压标准值（kN）；μz为风压高度变化系数；As为间隔棒受风面积（m2）。

2 稳定风作用下间隔棒防舞效果

模拟导线三角形排布线路在稳定风荷载作用下间隔棒防舞效果。设A相导线最低点离地面高度43 m，地面高10 m处基本风速7.74 m／s。考虑风速随高度变化，由于A、B相导线处于同一高度风速相同，而C相导线处风速大于A、B相。模拟获得线路安装间隔棒前后动力响应。模拟结果表明，三相导线舞动过程中的主振形均为单半波，位移幅值最大点在导线中点。间隔棒安装前后A相导线中点垂直、水平位移时程曲线见图3，各相导线中点舞动轨迹见图4。由两图看出，各相导线舞动轨迹均为椭圆形，为典型垂直舞动。间隔棒安装后对A、B相导线的舞动幅值影响较小，对C相导线影响较大。

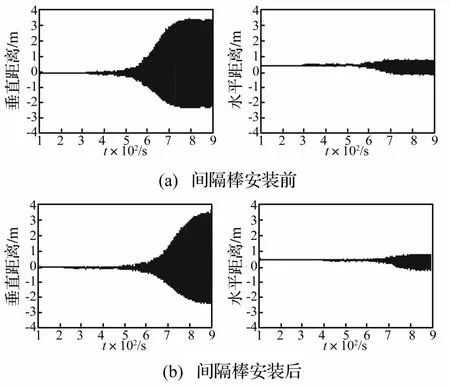
图3 稳定风作用下三角形排布线路A相导线中点位移时程Fig.3 Displacement time histories at midpoint of phase A in triangular arrangement under steady wind

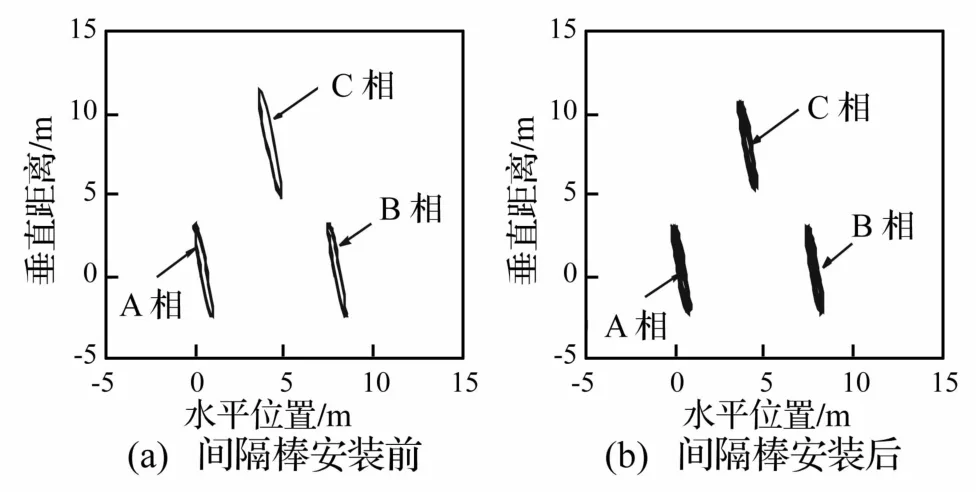
图4 稳定风作用下三角形排布线路各相导线中点的舞动轨迹Fig.4 Galloping trajectories at midpoint of each phase in triangular arrangement under steady wind

导线上安装防舞装置后的防舞效果可用振幅降低率 β评估［11］，即

式中：Ab，Aa为防舞装置安装前、后导线振动幅值。

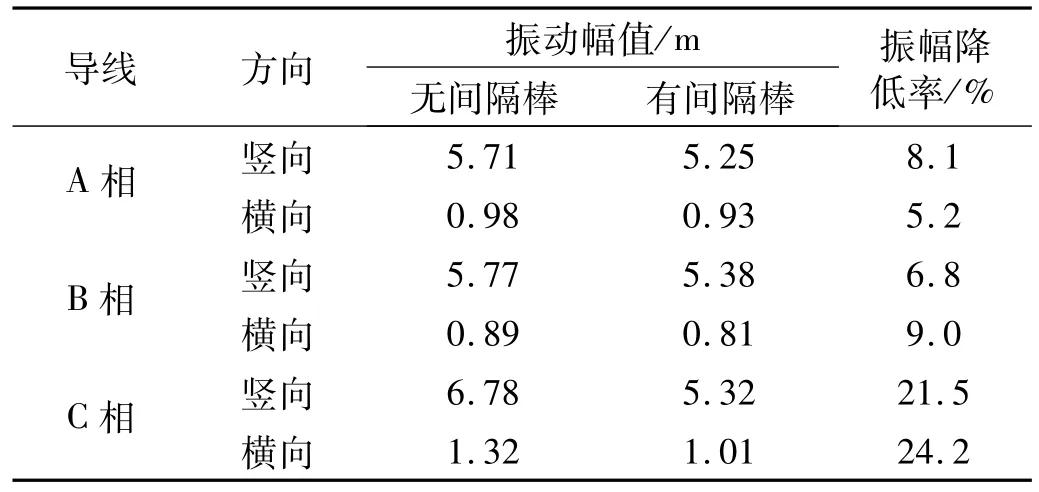
表2 稳定风作用下三角形排布线路间隔棒的防舞效果Fig.2 Anti－galloping efficiency of interphase spacers in triangular arrangement under steady wind

模拟所得三角形排布线路装有间隔棒的防舞效果见表2。由表2看出，在稳定风作用下间隔棒对C相导线舞动抑制作用较明显，而对A、B相导线舞动抑制效果较小；由于A、B相导线处于同一高度，风速一致，无间隔棒时该两相导线的竖向及水平振动幅值接近，而C相导线因风速较大，竖向、水平振动幅值明显大于其它两相导线。安装间隔棒后三相导线间相互制约，振动幅值接近，但C相导线振动幅值明显减小，表明抑制作用明显。

3 随机风场间隔棒防舞效果模拟分析

实际输电线路总处于随机风场中，由于风速变化的随机性及空间相关性，各子导线所受空气动力载荷会更复杂，导线舞动特征等可能不同。因此，为使模拟研究与实际更接近，须考虑风场的随机性。

3.1 随机风场模拟

模拟随机风时用工程中常用的考虑随高度变化的Kaimal脉动风速功率谱，并用Davenport相干函数计入空间不同位置风速的相干性［12］。据Shinozuka理论结合FFT算法，可快速有效模拟获得脉动风速时程样本［10］。设线路的风环境为B类地貌，地面粗糙系数取0.16，粗糙长度取0.03，湍流强度为0.18。与稳定风情况相同，设A相导线最低点离地面高度43 m，地面高10 m处基本风速7.74 m／s。模拟风速时每相导线沿顺线路水平方向每隔20 m模拟一个风速样本，模拟点坐标取每段对应的导线段中点坐标，模拟点从各相导线左端开始依次编号。模拟时程总长1000 s，时间步长0.5 s，频率截取范围0.0～6.28 rad／s，频率范围等分数3000。A相导线第5、C相导线第1模拟点风速时程曲线见图5。由图5看出，该两点的平均风速分别为9.88 m／s及10.20 m／s。将模拟所得脉动风速时程曲线进行谱分析可得功率谱，该两点模拟风速功率谱与Kaimal谱比较见图6，可见两者较吻合。

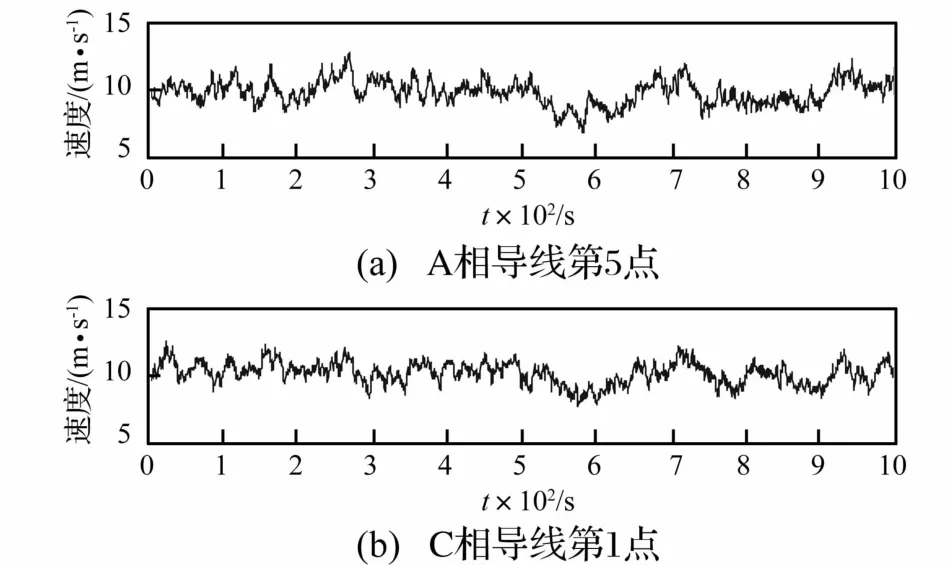
图5 三角形排布线路典型点处的随机风速时程Fig.5 Wind velocity histories at typical points of conductors in triangular arrangement under stochastic wind

模拟随机风场时一般忽略风速的纵向相干性［12］。由于A、B相导线高度相同，对模拟点的风速时程变化规律一致，但可认为两对应点风速存在时间差，即作用于B相导线的风滞后于A相导线，滞后时间由两相导线距离及风速确定。A、B、C三相导线第1个风速模拟点在时间段100～150 s中的风速时程见图7。由图7看出，C相导线离地面较高，平均风速较大，A、B相导线风速变化规律一致，但B相导线处风速滞后于A相导线。用类似方法可模拟获得三相导线垂直排布线路的随机风场。限于篇幅，不再赘述。

图6 典型模拟点随机风速功率谱与目标谱比较Fig.6 Comparison of power spectral of wind velocity and target spectrum at typical points under stochastic wind

图7 三角形排布线路三相导线第1模拟点典型时段风速时程Fig.7 Simulated wind velocity time histories at the first points in three phases

3.2 间隔棒防舞效果

用有限元方法模拟该两线路安装间隔棒前后在随机风场中的舞动过程。随机风场中三角形排布线路A相导线垂直、水平位移时程曲线见图8。由图8看出，在随机风场中导线舞动振幅随时间不断变化，用振幅最大值比较安装间隔棒后的防舞效果欠妥。为此，通过统计各振动周期振幅，计算其均方根（RMS）值，代入式（3）计算振幅降低率。两种排布线路安装间隔棒前后各相导线舞动过程中档中点振幅的RMS值及振幅降低率见表3。由表3看出，两种导线排布线路安装间隔棒后，对各相导线舞动均有较明显抑制作用。由于两线路均发生垂直舞动，其竖向位移抑制更重要，可认为在研究的间隔棒安装方式下对三角形排布线路防舞效果较垂直排布好。原因为由于三角形排布时线路整体刚度大于垂直排布，系统稳定性更好。

图8 随机风场中三角形排布线路A相导线中点位移时间历程Fig.8 Displacement time histories at midpoint of phase A in triangular arrangement under stochastic wind

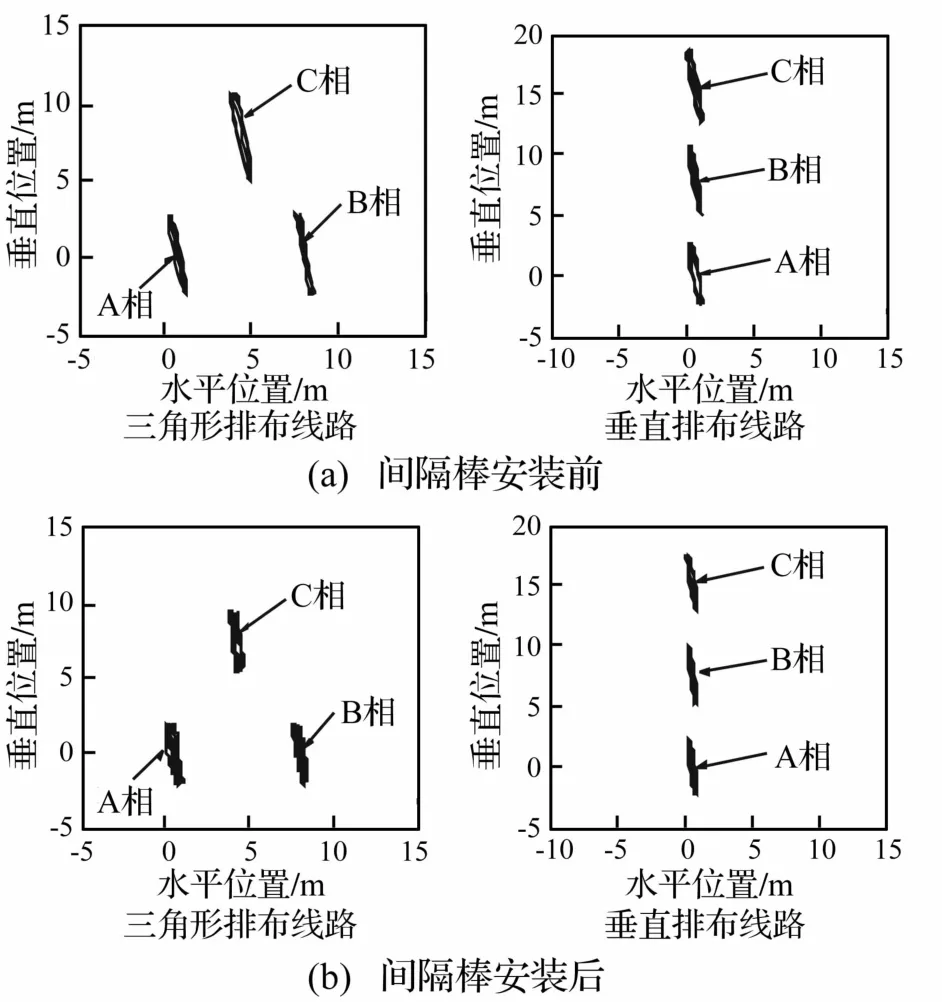
图9 随机风场中两线路各相导线中点舞动轨迹Fig.9 Galloping trajectories at midpoint of each phase in two arrangements under stochastic wind

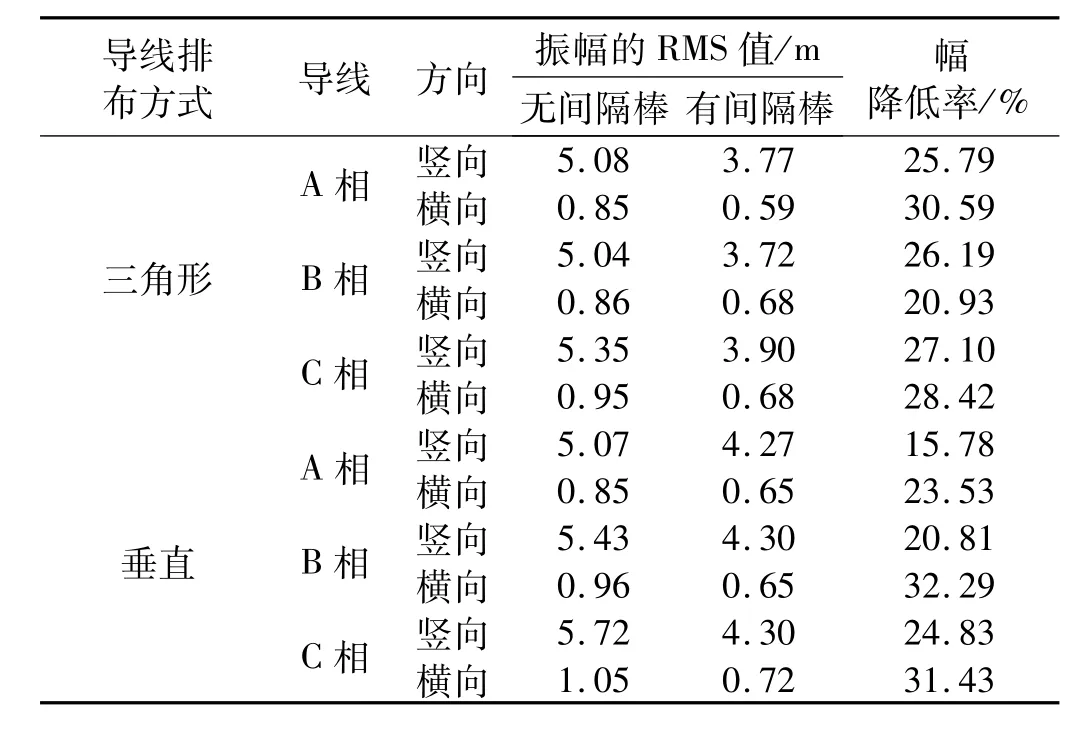
表3 随机风作用下间隔棒防舞效果Tab.3 Antigalloping efficiency of interphase spacer under stochastic wind

两种排布线路安装间隔棒前后各相导线舞动轨迹见图9。由图9看出，安装间隔棒后各相导线舞动幅值明显减小，且仍为垂直舞动，运动轨迹仍为椭圆。

4 结 论

本文用有限元数值模拟方法研究双分裂线路中间隔棒防舞效果，结论如下：

（1）研究间隔棒防舞效果时，稳定风荷载难以反映各相导线运动的差异性，故须考虑随机风荷载；

（2）基于随机风场中三角形、垂直排布线路安装间隔棒前后舞动过程的数值模拟，用振幅降低率评估防舞效果发现，三角形排布线路的防舞效果较垂直排布好；

（3）为提高间隔棒对舞动的防治效果，可用本文方法对防舞技术进行优化研究。

［1］郭应龙，尤传永，李国兴.输电线路舞动［M］.北京：中国电力出版社，2003.

［2］Lilien JL.State of the art of conductor galloping［M］.Paris：CIGRE，2007.

［3］Van Dyke P，Laneville A.Galloping of a single conductor covered with a Dsection on a highvoltage overhead test line［J］. Journal of Wind Engineering and Industrial Aerodynamics，2008，96（6／7）：1141－1151.

［4］Hou L，Wang L，Yan D，et al.Mechanical parameter optimization of interphase composite spacers used for controlling congductor galloping［R］.Annual Report Conference on Electrical Insulation and Dielectric Phenomena，Vancouver，BC，Canada，2007：304－307.

［5］Kim H S，Nguyen T L.Analysis of galloping amplitude for conductors with interphase spacers［C］.Proceedings of The 30th Annual Conference of IEEE Industrial Electronics Society，Busan，Korea，2004：1520－1525.

［6］Fan Z，Hao S，Zhou K，et al.Effect of interphase composite spacers on transmission line galloping control［C］.Second International Conference on Digital Manufacturing＆Automation，IEEE Computer Society，China，2011：485－488.

［7］国家电力公司东北电力设计院.电力工程高压送电线路设计手册（第二版）［M］.北京：中国电力出版社，2003.

［8］严波，胡景，周松，等.覆冰四分裂导线舞动数值模拟及参数分析［J］.振动工程学报，2010，23（3）：310－316.YAN Bo，HU Jing，ZHOU Song，et al.Numerical simulation and parameter analysis of galloping for iced quadbundled conductor［J］.Journal of Vibration Engineering，2010，23（3）：310－316.

［9］Hu Jing，Yan Bo，Zhou Song，et al.Numerical investigation on galloping of iced quad bundle conductors［J］.IEEE Transactions on Power Delivery，2012，27（2）：784－792.

［10］Yan Bo，Lin Xuesong，Luo Wei，et al.Numerical study on dynamic swing of suspension insulation in overhead transmission line under wind load［J］.IEEE Transactions on Power Delivery，2010，25（1）：248－259.

［11］胡景，严波，祖正华，等.一种新型防舞器及其机理研究［J］.工程力学，2011，28（9）：200－206.HU Jing，YAN Bo，ZU Zhenghua，et al.A new antigalloping device and investigation on its mechanism［J］.Engineering Mechanics，2011，28（9）：200－206.

［12］ Simiu E，Scanlan R H.Wind effects on structures（2rd edition）［M］.New York：John Wiley＆Sons，1986.