圆形区域多圆孔对SH波散射Green函数解

史文谱，魏 娟

（1.烟台大学 机电汽车工程学院，烟台 264005；2.山东省高校先进制造与控制技术重点实验室，山东 264005）

Green函数法作为求解数学物理方程问题的重要方法应用非常广泛，如流体问题［1］、Possion方程边值问题［2］、裂纹问题［3－4］、动态载荷区间识别问题［5］及电磁波电阻率测量问题［6］等。又如利用Green函数法及复变函数法研究界面脱胶圆夹杂对SH波散射的远场解［7］；借助空间契合思想与Fredholm积分方程理论研究双相压电介质中交界面附近圆孔边界处环向动应力集中系数与环向电场强度集中系数的变化规律［8］；基于饱和介质三维波动理论的Biot模型，采用傅里叶积分变换与Hankel变换及算子理论研究横观各向同性饱和土中柱面载荷的动力Green函数问题，并给出柱坐标系下横观各向同性饱和土中波动方程非轴对称通解［9］；而有关圆形区域内含多圆孔缺陷的SH波散射问题研究较少见。本文利用波函数展开法、复变函数法及Graf加法公式，讨论圆形区域内含多圆孔缺陷时在圆形域边界处作用反平面线源载荷条件的Green函数解。结果可广泛用于与圆形区域内含夹杂SH波散射问题研究，具有重要理论意义。

1 问题模型分析

建立坐标系xoy见图1，半径为R的圆形区域介质内有 N个半径为 Rj（j＝1，2，…，N）的圆孔缺陷，其圆心oj（j＝1，2，…，N）在坐标系 xoy中的位置向量设为 rj0＝（rj0，θj0），对应的复数坐标为 Zj0＝rj0exp（iθj0）。以圆心建立局部坐标系xjojyj。圆形区域介质剪切模量、质量体密度为μ，ρ。圆形区域外边界Γ作用的反平面脉冲线源设为 δ（r－R0）e－iωt，R0＝（R，θ0）（θ0为边界 Γ的脉冲线源作用位置方位角）。

对反平面SH波散射问题而言，位移场 u（r，θ，t）＝U（r，θ）exp（－iωt）中位移幅度函数 U（r，θ）满足 Helmholtz方程，即

式中：2为Laplace算子；K＝ω／V为波数；ω为载荷扰动圆频率；V＝（μ／ρ）1／2为介质内波速。

在圆形区域外边界Γ的稳态线源载荷δ（r－R0）e－iωt作用下，各圆孔分别产生一向外传播的散射波，且均满足式（1），可表为

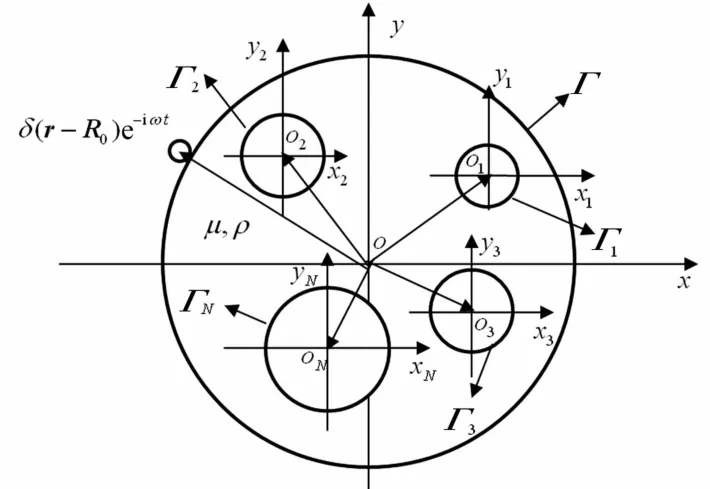
图1 圆形区域内多圆孔对SH波散射Fig.1 Scattering of several cavities in circular domain to SHwave

圆形区域边界Γ本身在介质内会激发一驻波（考虑波场在o点处的有界性），可表为

介质内应力场 τrz，τθz与波函数幅度函数 U（Z，Z）关系为

对各圆孔散射波幅度函数而言，本文用Graf加法公式。当需利用Γ处边界条件时，特殊函数加法公式为

第i个圆孔产生的波函数转换到第j个局部坐标系时所用特殊函数加法公式为

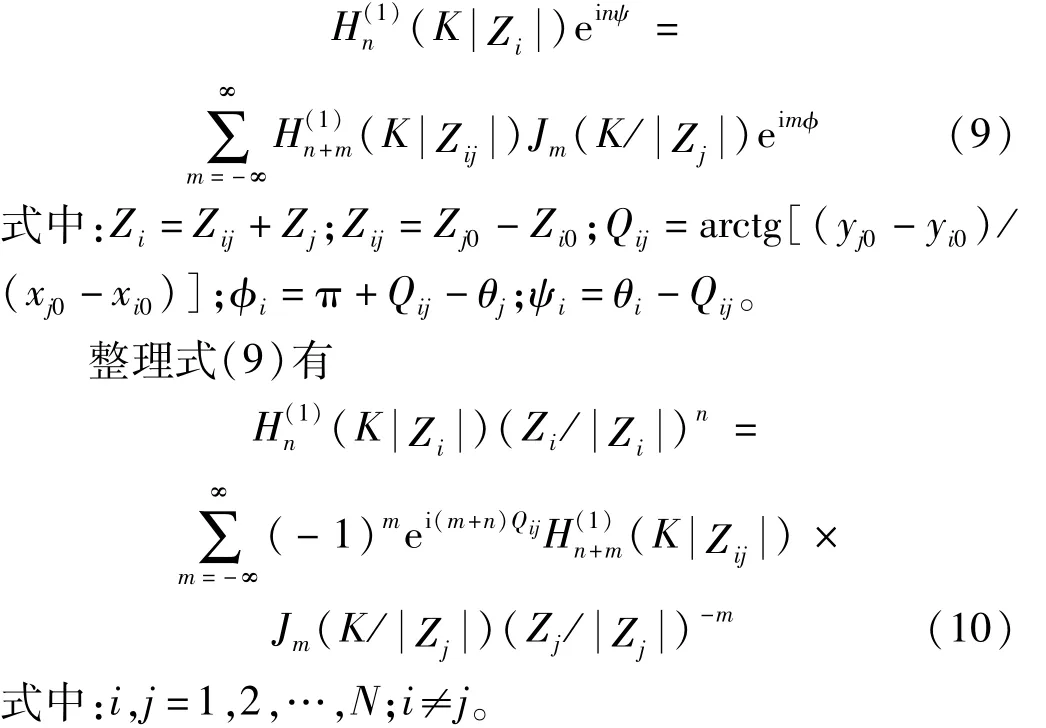
联立式（4）～式（6）得定解方程组为

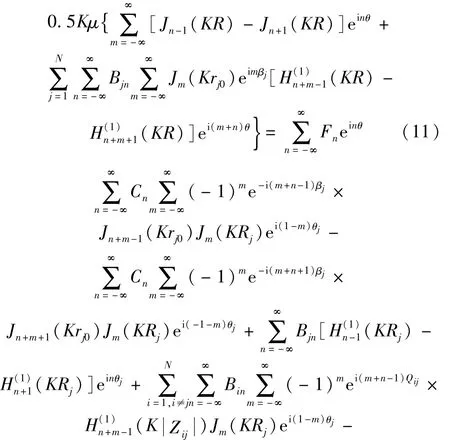
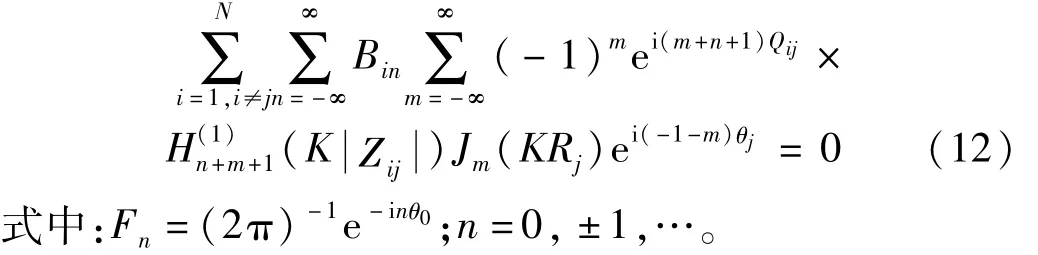
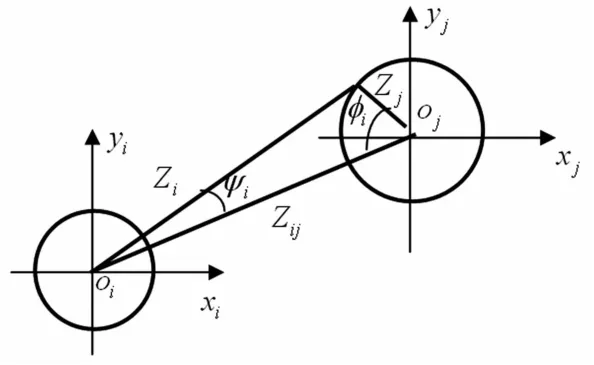
图2 第i，j局部坐标系间多极坐标变换Fig.2 Multicoordinate transform between i－th and j－th local coordinate system

对式（11）、（12）两边分别乘以 e－iqθ，e－iqθj（q＝0，±1，…），并在区间［－π，π］内积分得

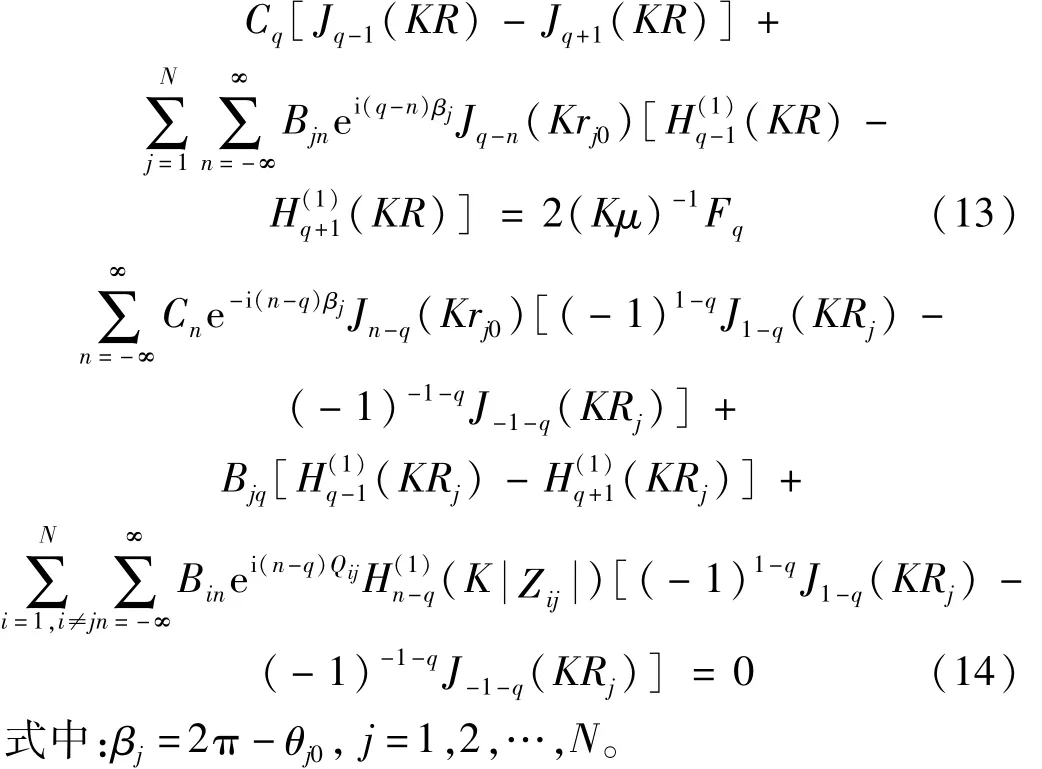
求解式（13）、（14）可得未知系数 Cn，Bjn（n＝0，±1，…；j＝1，2，…，N），从而确定介质内 Green函数解。

圆孔 1边界处环向动应力 τr1z（R1，θ1）可表示为

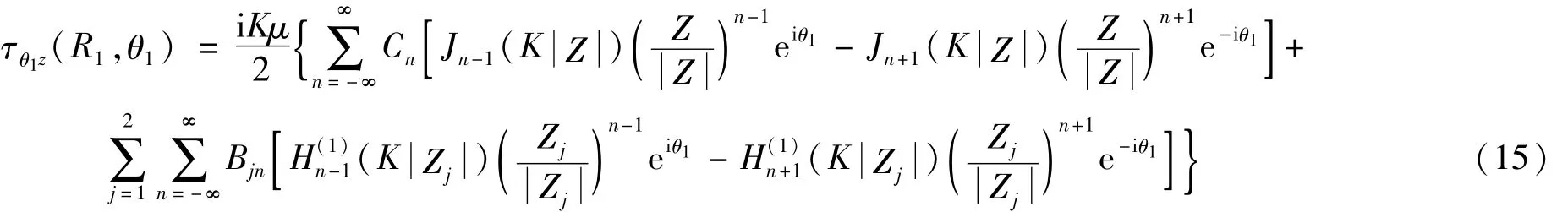
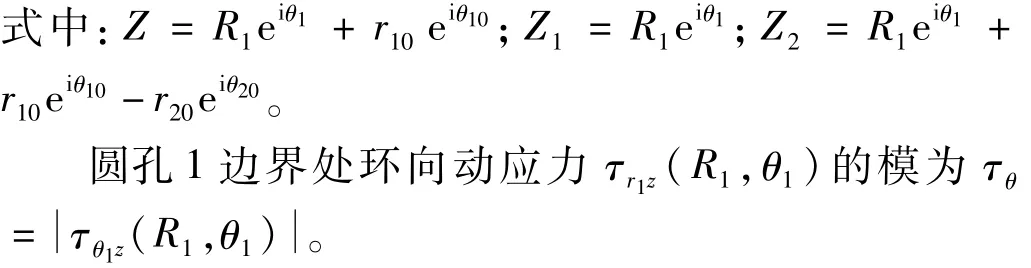
2 算例与分析

图3 圆管外边界受反平面稳态载荷作用时动力响应Fig.3 Dynamic response of the pipe with steady outplane loading acting on its exterior boundary

考虑圆形区域内有两个不相交的圆孔 1、2（图 1），已知参数 μ＝6×106N／m2，R＝10 m，R1＝3 m，R2＝4 m，r10＝4 m，r20＝5 m，波数 K取 0.05，0.2，0.35，0.5。分析圆孔1边界处环向动应力模τθ的变化及分布。θ10＝0，θ20＝π，θ0＝0时，计算结果见图4（a）；θ10＝π，θ20＝0，θ0＝0时，计算结果见图 4（b）；θ10＝π，θ20＝0，θ0＝π／2时，计算结果见图 4（c）。由图4（a）、（b）看出，由于两圆孔中心线经过线源载荷位置，故结果对称（对称于 0°～180°）；由图 4（c）看出，因两圆孔中心线不经过线源载荷位置，结果不对称。由此知低频响应普遍不明显。为进一步说明本文方法及结论的正确性，选数学物理方程定解问题作为对比算例，见图3。

式中：r2为圆管内半径；r1为圆管外半径；f（θ）为外部分布载荷幅度函数；x为介质点位置向量，定义x＝（r，θ）；μ为圆管材料剪切模量。

取 f（θ）＝3cos（2θ）分析管内边界处环向动应力幅度模τθ随无量纲波数Kr2（K为波数）变化情况。由数学物理方法得定解问题理论解为

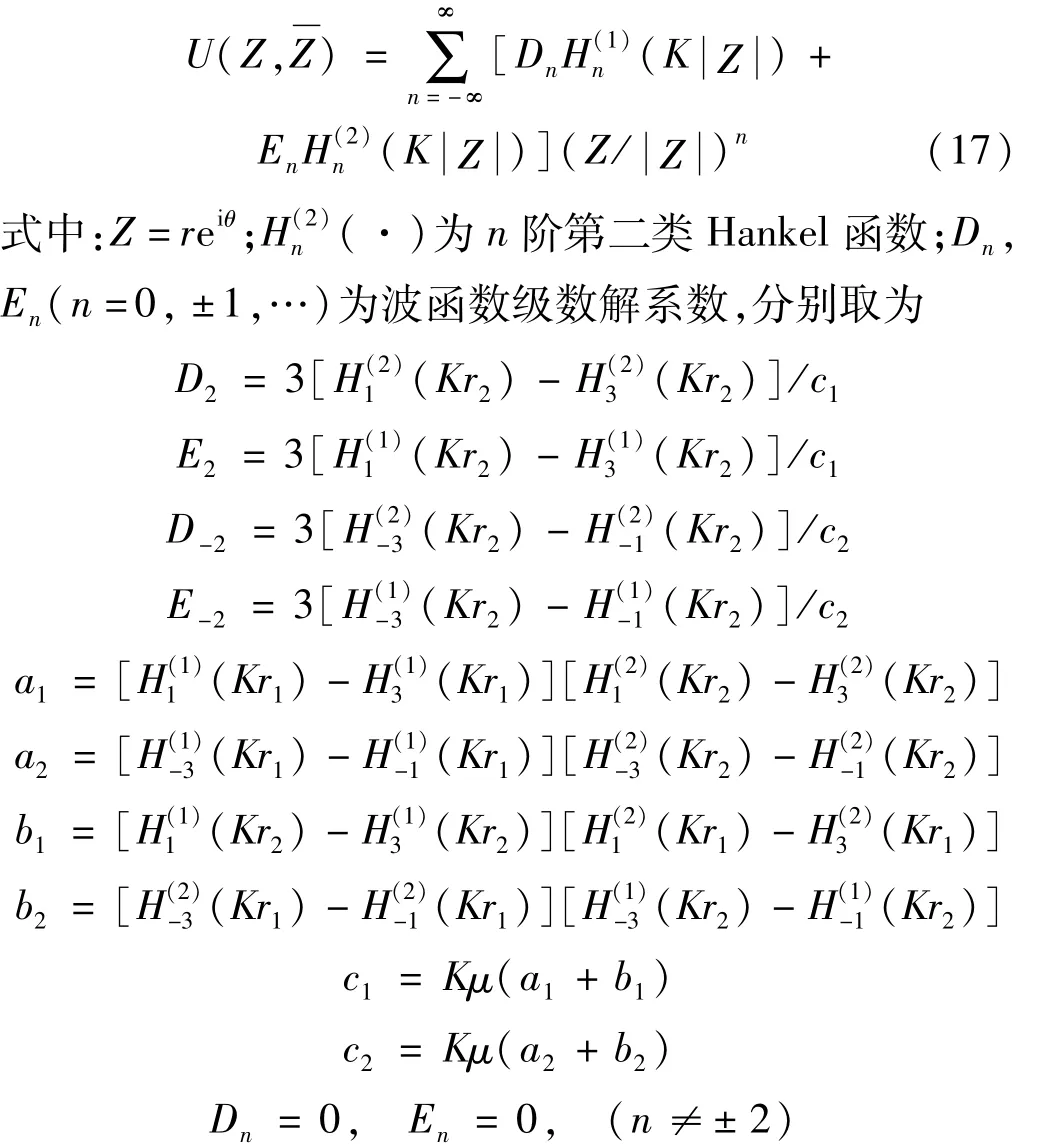
管内边界处动应力幅度模形式为

若取μ＝6×106N／m2，r1＝10 m，r2＝3 m，波数 K取0.05，0.2，0.35，0.5，则理论解与本文 Green函数积分解（N＝1，r10＝0）计算结果见图4（d）。由图4（d）看出，两者在计算精度范围内完全一致，说明本文方法有效、可行。

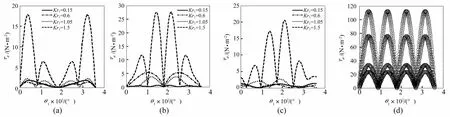
图4 圆孔边界处环向应力幅度变化Fig.4 Variations of the hoop stress of the points on the boundary of the number one circular cavity

3 结 论

（1）本文针对圆形区域外边界处作用反平面线源载荷时其内部多圆孔缺陷对SH波散射的Green函数解问题进行研究，利用复变函数法、波函数展开法及Graf加法公式提出的解析求解方法，亦适用于线源作用在某个内部圆孔边界情形。所得Green函数解对采用大圆逼近直边界法研究双相介质界面附近圆形夹杂及孔洞对SH波散射问题有重要参考意义。

（2）该方法计算收敛速度快、精度高。通过具有理论解的数学物理定解问题验证方法、结论的正确性。圆形区域外边界处作用反平面分布载荷时，利用叠加原理结合本文Green函数解可直接给出问题的积分解。

［1］Manyanga D O，Duan W Y.Green functions with pulsating sources in a twolayer fluid of finite depth［J］.China Ocean Eng.，2011，25（4）：609－624.

［2］陈秀武.Poisson方程边值问题的Green函数法［J］.甘肃联合大学学报（自然科学版），2008，22（1）：122－124.CHEN Xiuwu.Green function’s method of poisson equation boundary conditions questions［J］.Journal of Gansu Lianhe University（Natural Sciences），2008，22（1）：122－124.

［3］齐辉，张根昌，陈冬妮，等.SH波入射时半空间界面裂纹与圆形衬砌的相互作用［J］.爆炸与冲击，2012，32（5）：463－469.QI Hui， ZHANG Genchang， CHEN Dongni， et al.Scattering of SHwave by the circular lining with an interface crack in a bimaterial halfspace［J］.Explosion and Shock Waves，2012，32（5）：463－469.

［4］崔元庆，杨卫，仲政.半无限平面裂纹构型横向应力的Green函数［J］.应用数学和力学，2011，32（8）：912－919.CUI Yuanqing， YANG Wei， ZHONG Zheng. Green’s function for tstress of a semiinfinite plane crack［J］.Applied Mathematics and Mechanics，2011，32（8）：912－919.

［5］王晓军，杨海峰，邱志平，等.基于Green函数的动态载荷区间识别方法研究［J］.固体力学学报，2011，32（1）：95－101.WANG Xiaojun， YANG Haifeng，QIU Zhiping， et al.Research on interval identification method for dynamic loads based on Green’s function［J］.Applied Mathematics and Mechanics，2011，32（1）：95－101.

［6］杨锦舟，魏宝君，林楠.径向成层介质的Green函数及其在随钻电磁波电阻率测量的应用［J］.中国石油大学学报（自然科学版），2009，33（3）：53－58.YANG Jinzhou，WEI Baojun，LIN Nan.Green’s function for radial stratified media and its application to electromagnetic wave resistivity measurement while drilling tool［J］.Journal of China University of Petroleum，2009，33（3）：53－58.

［7］赵嘉喜，齐辉.界面脱胶圆夹杂对SH波散射的远场解［J］.力学与实践，2009，31（1）：47－51.ZHAO Jiaxi，QI Hui.Far field solution of SHwave scattered by an interface cylindrical inclusion with disconnected curve［J］.Mechanics in Practice，2009，31（1）：47－51.

［8］李冬，宋天舒.双相压电介质中界面附近圆孔的动态性能分析［J］.振动与冲击，2011，30（3）：91－95.LI Dong，SONG Tianshu.Dynamic perfermance analysis of circular cavity near interface in piezoelectric bimaterials［J］.Journal of Vibration and Shock，2011，30（3）：91－95.

［9］王小岗.横观各向同性饱和土中柱面载荷的动力Green函数［J］.力学学报，2010，42（5）：909－918.WANG Xiaogang.Dynamic Green’s function for internal barrel loads in transversely isotropic saturated soils［J］.Chinese Journal of Theoretical and Applied Mechanics，2010，42（5）：909－918.