利用独立性约束非负矩阵分解的高光谱解混算法

杨秀坤，王东辉

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

高光谱图像的主要特点是，成像光谱仪将图像维和光谱维信息融合为一体，其探测波段几乎以纳米和亚微米级的光谱分辨率覆盖了可见光、近红外、短波红外、中波红外和热红外等全部光谱区[1]。由于空间分辨率的限制以及地物的复杂多样性，一个像元内往往会包含多种地物类型，称为混合像元。混合像元分解是高光谱研究的重要课题。为了提高对真实地表覆盖的描述准确性，需要对混合像元进行分解，计算一种地物类型(端元)在该像元中所占的比例(丰度)。由于非负矩阵分解NMF(nonnegative matrix factorization)[2]不需要假设原始数据的概率密度分布等先验信息，利用非负约束获取数据，因此，基于统计学方法的NMF近年在高光谱解混中受到关注。因为目标函数具有非凸性，NMF存在局部极小值，采用惩罚函数法，需要根据应用领域的特点增加辅助约束条件克服该缺点。目前，已经提出了平滑性[3]、最小体积(MVCNMF)[4]、分段平滑和丰度稀疏(PSSCNMF)[5]、最小丰度协方差[6]、端元光谱差距[7]等约束条件。独立成分分析ICA(independent component analysis)[8]基于信号高阶统计特性，将数据线性分解为统计独立的成分。混合像元中各端元光谱相互独立，因此，可将度量端元光谱数学期望的非高斯性的四阶累积量和负熵约束应用于非负矩阵分解，提出了一种端元光谱独立性约束的NMF方法，I-NMF(independent nonnegative matrix factorization)，适用于没有纯像元的情形。

1 基于端元光谱独立性约束非负矩阵分解

1.1 线性光谱混合模型

线性光谱混合模型(linear spectral mixture model, LSMM)是混合像元分解的常用方法。这种模型计算简单、应用最为广泛。在线性模型中，混合光谱是端元光谱与其比例的线性组合。设X为像元光谱矢量，S=[s1s2…sN]为端元光谱矩阵，A=[a1a2…aN]T是N维矢量，其各分量元素为对应端元丰度，N为随机噪声。线性光谱混合模型为

(1)

1.2 非负矩阵分解

NMF算法通过最小化欧式距离目标函数，在已知X的情况下解得S和A的最优解：

(2)

迭代公式为

(3)

基于NMF的光谱解混算法属于端元生成(endmember genera-tion algorithm, EGA)算法，不需要假定存在纯像元，在提取端元的同时获得相应的丰度。

因NMF分解算法式(1)具有非负性限制，其主要缺陷是容易陷入局部最小值，并且分解结果具有幅度上的不确定性[7]。I-NMF算法以端元光谱之间的独立性为约束条件，使得目标函数综合了图像的分解误差和端元光谱的影响。

1.3 端元光谱数学期望的四阶累积量约束

统计论的中心极限定理规定，一组独立随机变量和的分布比任何信号更接近高斯分布，可将非高斯性作为随机信号相互独立的度量。四阶累积量是一种典型的非高斯性测度，在理论和计算上简单，易于实现[9]。非高斯随机变量有正有负，采用端元光谱数学期望的四阶累积量绝对值作为约束条件:

(4)

(5)

I表示其分量都为1的向量，即IN=[1 1 … 1]∈UN。由于X需进行中心化和白化预处理，则si的数学期望为0，均方差为1。迭代中用瞬时值代替数学期望计算，该约束应被最大化，将该约束求导数，整理可得到

(6)

(7)

1.4 端元光谱数学期望负熵约束

仅考虑式(5)作为非负矩阵分解的约束条件不能获得理想解混精度，还需要增加端元光谱的负熵约束。信息论中，各信息分量的独立性可用互信息表示，互信息最小等同于负熵最大。端元光谱负熵可用一种非线性函数组合逼近[10]:

(8)

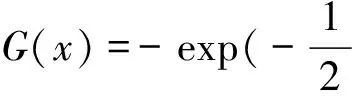
(9)

1.5 I-NMF算法描述

增广式(4)，I-NMF的目标函数为

(10)

式中：λ1、λ2为权值。

约束条件(惩罚函数)J1(S)、J2(S)保证端元光谱具有较大的独立性，使其接近真实的端元光谱。目标函数综合考虑了最小近似误差和端元光谱惩罚函数的限制条件。权值λ1、λ2调整分解的重构误差与惩罚函数J1(S)、J2(S)之间的关系。式(10)等号后的第1项保证尽可能小的分解误差，而惩罚函数保证所提取的端元光谱接近真实的端元光谱，从而获得全域最优解。

通过NMF线性混合模型式(1)非负性约束得到满足，为满足式(1)和为1约束，采用文献[12]的方法：

(11)

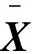
I-NMF的投影梯度迭代公式为

(12)

投影函数[13]选择为PΩ(x)=max(0,x)

2 仿真实验

2.1 性能指标

光谱角距离(spectral angle distance, SAD)和均方根误差(root mean square error, RMSE)常被用来计算光谱和丰度解混估计值与真实值的近似程度，并用其来衡量解混效果。对于第i个端元，SAD定义为

(13)

RMSE定义为

(14)

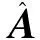
2.2 模拟数据实验

从USGS矿物光谱库中选取5种线性独立的端元光谱(明矾石、水铵长石、方解石、高岭石、白云母)，按Dirichlet分布混合，端元丰度之和进行归一化，加上不同的白噪声，形成模拟实验数据。

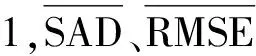
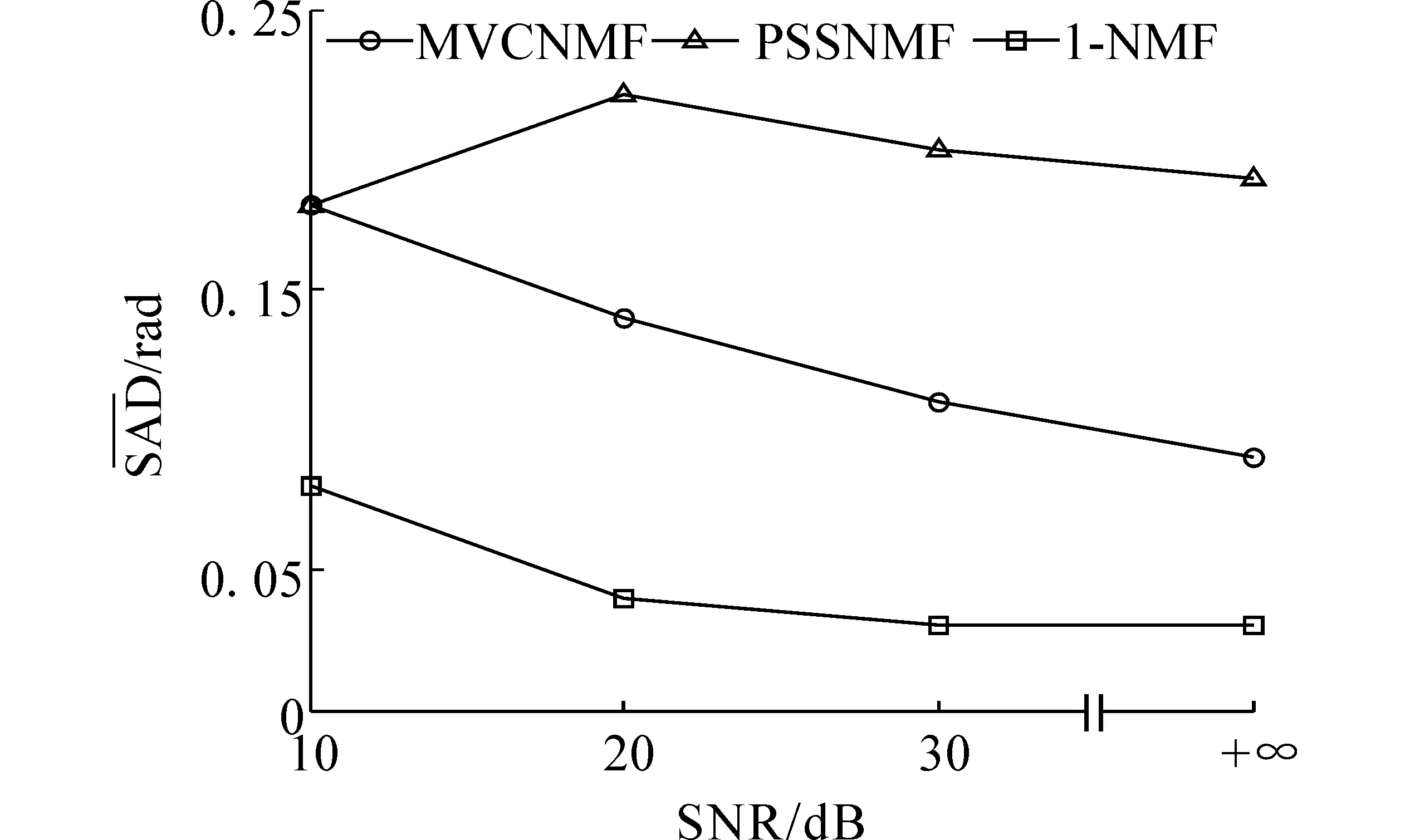
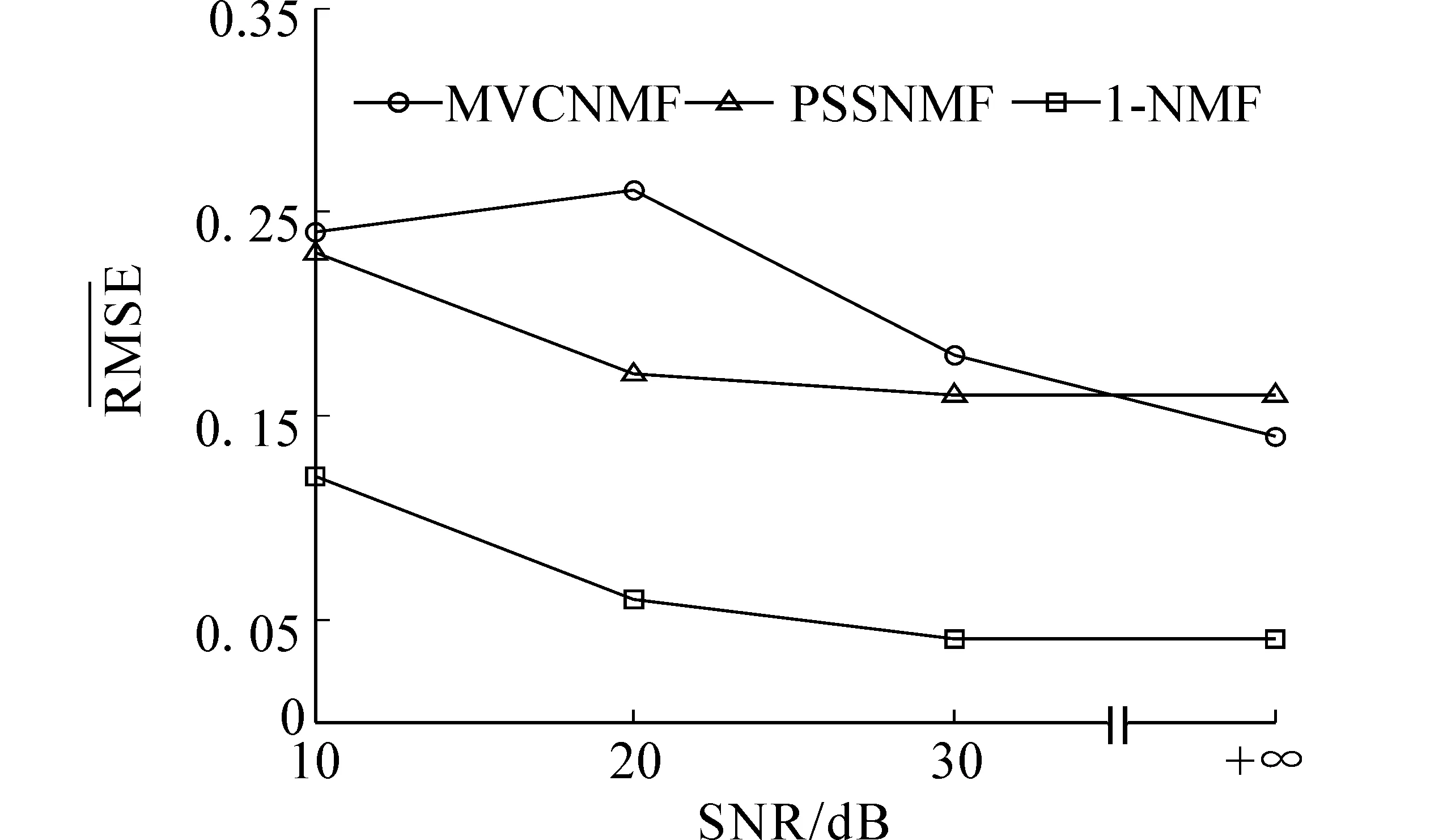
不同像元个数解混性能实验：像元个数不同时，I-NMF与MVCNMF、PSSCNMF算法解混性能比较，如图2。像元数目H分别为1 600、3 600、6 400、10 000，信噪比固定为20 dB。

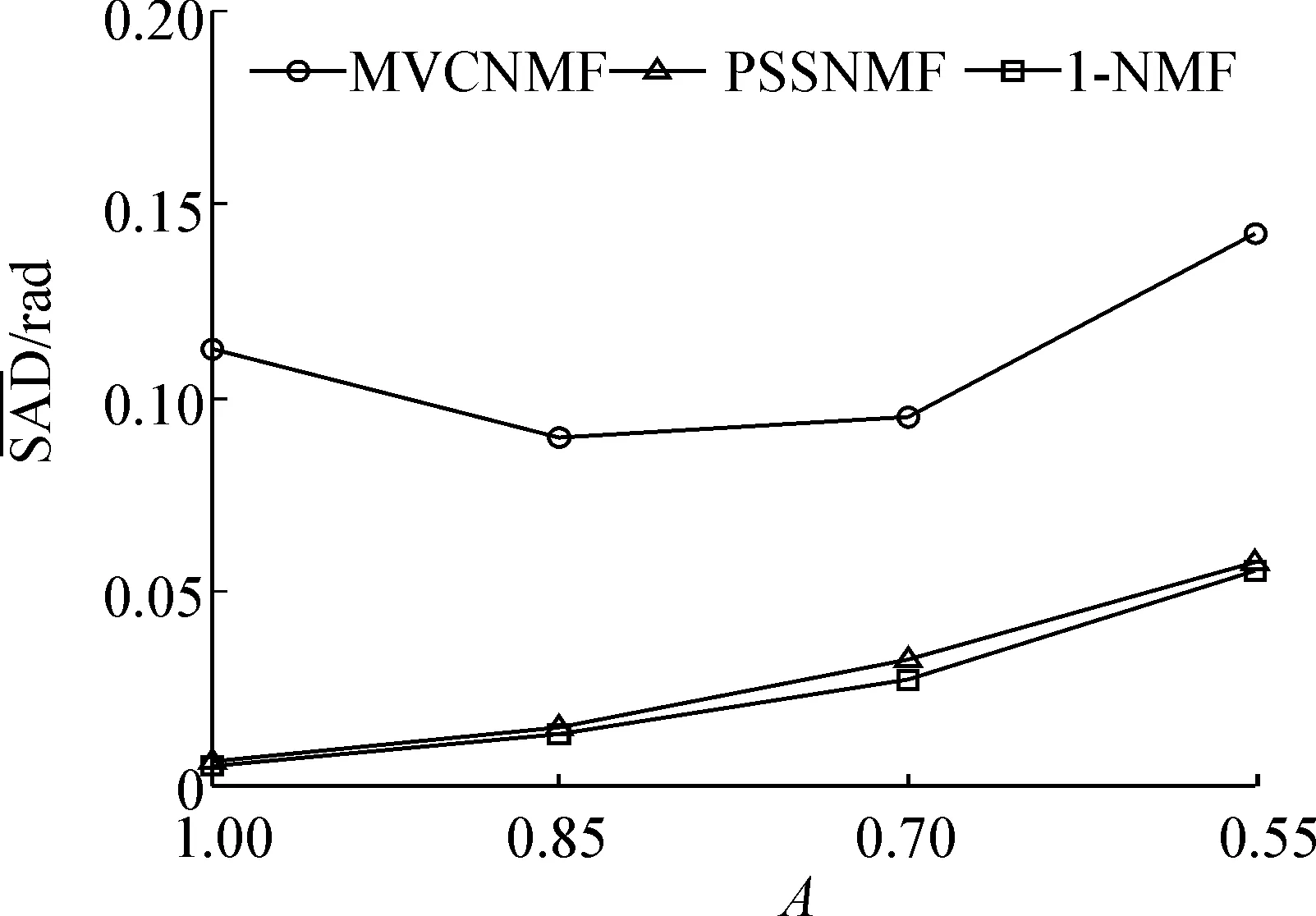
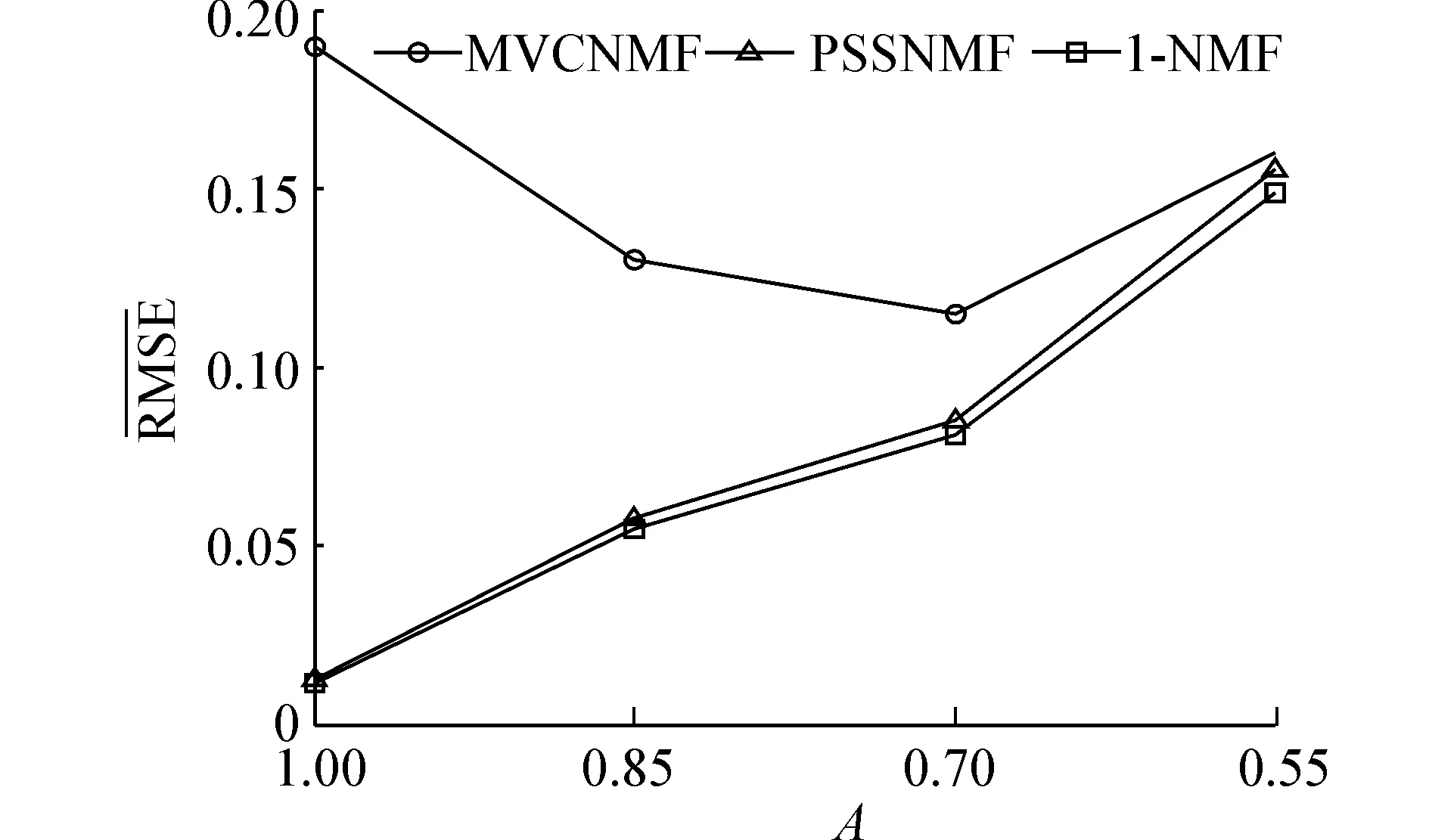
无纯像元情况的解混性能实验：对I-NMF与MVCNMF、PSSCNMF算法在无纯像元时解混性能比较，如图3。全部端元的丰度A从1降到0.55(1表示数据中存在纯像元)，信噪比为30 dB。观察实验结果，I-NMF算法解混性能要优于MVCNMF、PSSCNMF算法。

2.3 真实数据实验

采用美国JPL实验室的AVIRIS获得的内华达州Cuprite高光谱图像，图4为第183、193、207波段图像合成的伪彩色图像。去除信噪比低和水蒸气吸收波段余下188个有效波段。文献[14]给出了该地区的真实地物分布。

图4 Cuprite伪彩色图像

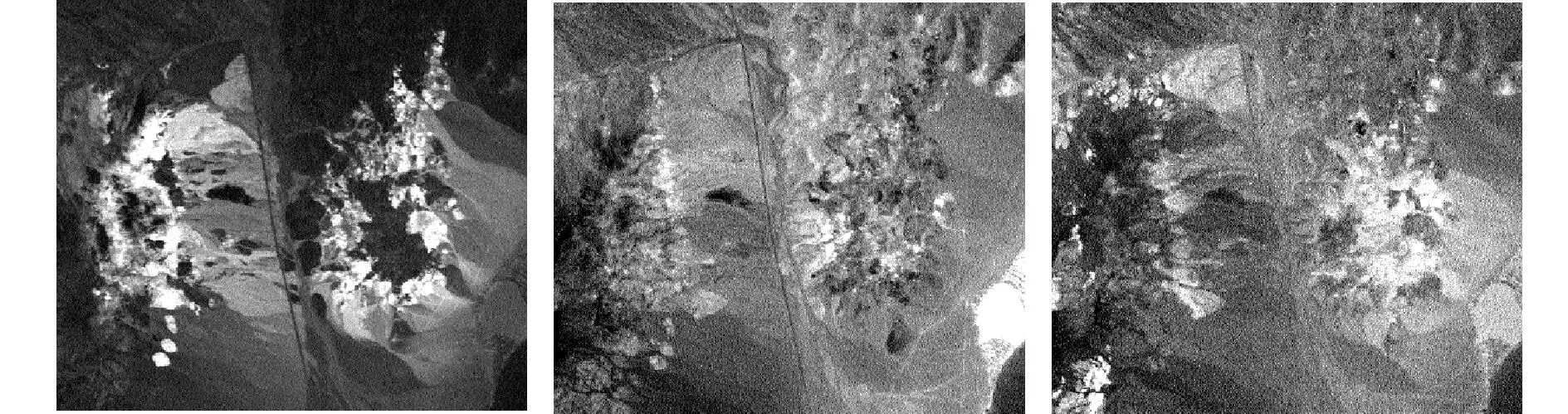
(a)明矾石 (b)水铵长石 (c)方解石

(d)黄钾铁矾 (e)高岭石 (f)蒙脱石

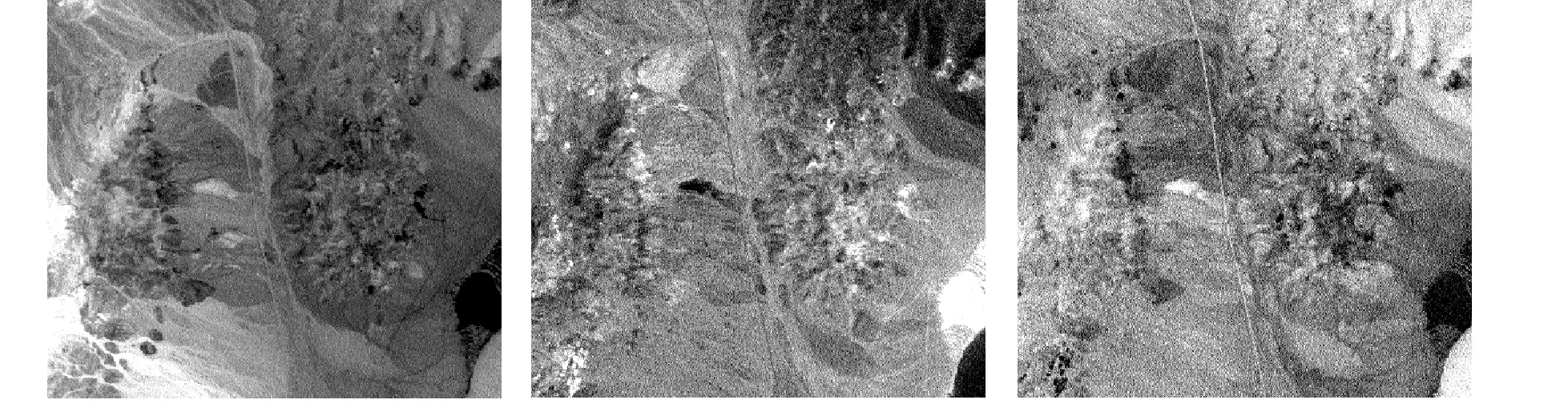
(g)白云母 (h)绿脱石 (i)榍石

表1 Cuprite数据的光谱角比较

3 结束语

针对线性混合像元分解的特点，提出一种基于独立性约束的非负矩阵分解的混合像元分解方法。该方法适用于无纯像元的情况。通过模拟数据与真实数据实验分析，表明本文提出的方法能够提高混合像元分解的精度。投影梯度算法的收敛速度较慢，需采用更有效的优化算法来提高解混的效率。

参考文献：

[1]杜培军，谭琨，夏俊士. 高光谱遥感影像分类与支持向量机应用研究[M]. 北京：科学出版社，2012:6-9.

[2]LEE D D, SEUNG H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature, 1999, 401:788-791.

[3]刘雪松，王斌，张立明. 基于非负矩阵分解的高光谱遥感图像混合像元分解[J]. 红外与毫米波雷达学报，2011，30(1):27-32.

LIU Xuesong, WANG Bin, ZHANG Liming. Hyperspectral unmixing based on nonnegative matrix factorization[J]. J Infrared Millim Waves, 2011, 30(1):27-32.

[4]MIAO Lidan, QI Hairong. Endmember extraction from highly mixed data using minimum volume constrained nonnegative matrix factorization[J]. IEEE Trans Geosci Remote Sens, 2007, 45(3):765-777.

[5]贾森，钱沄涛，纪震，等. 基于光谱和空间特性的高光谱解混方法[J]. 深圳大学学报:理工版，2009, 26(3):262-267.

JIA Sen, QIAN Yuntao, JI Zhen, et al. Spectral and spatial character-based hyperspectral unmixing[J]. Journal of Shenzhen University:Science and Engineering, 2009, 26(3):262-267.

[6]赵春晖，成宝芝，杨伟超. 利用约束非负矩阵分解的高光谱解混算法[J]. 哈尔滨工程大学学报，2012, 33(3):377-382.

ZHAO Chunhui，CHENG Baozhi，YANG Weichao. Algorithm for hyperspectral unmixing using constrained nonnegative matrix factorization[J]. Journal of Harbin Engineering University, 2012, 33(3):377-382.

[7]吴波，赵银娣，周小成. 端元约束下的高光谱混合像元非负矩阵分解[J]. 计算机工程，2008, 34(22):229-233.

WU Bo，ZHAO Yindi，ZHOU Xiaocheng. Unmixing mixture pixels of hyperspectral imagery using endmember constrained nonnegative matrix factorization[J]. Computer Engineering, 2008, 34(22):229-233.

[8]HYVARINEN A, KARHUNEN J, OJA E. Independent component analysis[M]. New York: Wiley, 2001:1-5.

[9]李娜，赵慧洁. 高光谱数据非监督分类的改进独立成分分析方法[J]. 国土资源遥感，2011, 89(2):70-74.

LI Na, ZHAO Huijie. An improved independent component analysis method for unsupervised classification of hyperspectral data[J]. Remote Sensing for Land & Resources,2011, 89(2):70-74.

[10]路威，余旭初，马永刚，等. 高光谱遥感影像海上舰船目标检测算法的研究[J]. 海洋测绘，2005, 25(4):8-12.

LU Wei, YU Xuchu, MA Yonggang, et al. Research of sea fleet targets detection approach in hyperspectral image[J]. Hydrographic Surveying and Charting, 2005, 25(4):8-12.

[11]ARNAVUT Z, NARUMALANI S. Lossless compression of multispectral images using permutations[C]//IEEE IGARSS ’96, 1996:463-465.

[12]HEINZ D C, CHANG C I. Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery[J]. IEEE Trans Geosci Remote Sens, 2001, 39(3):529-545.

[13]GILLIS N, GLINEUR F. Using under-approximations for sparse nonnegative matrix factorization[J]. Pattern Recognition, 2010, 43(4):1676-1687.

[14]CIARK R N, SWAYZE G A. Evolution in imaging spectroscopy analysis and sensor signal-to-noise: an examination of how far we have come[C/OL]//The 6th Annual JPL Airborne Earth Science Work Shop, 1996. http://speclab.cr.usgs.gov/PAPERS.imspec. evol/aviris.evolution.html.