基于峰后特征的深部隧道围岩分层断裂数值分析*

苏永华，毛克明，梁 斌，付 雄，贺 炜

(1. 湖南大学 土木工程学院，湖南 长沙 410082; 2. 长沙理工大学 土木与建筑学院，湖南 长沙 410114)

由于煤炭、石油、国防以及核废料处理等领域向地层深部或超深部挺进，深部岩体的开挖变形问题已引起了岩土工程界的广泛重视.传统的观测和理论公认，地下工程开挖后仅在靠近临空面围岩形成单一破裂带.但在深部工程开挖及相关试验中，发现围岩表现出不同于浅部工程的破裂区域分布，即非经典破裂现象.

俄罗斯学者E.I.shemyakin等[1]通过模型试验获得了分区破裂化现象，并在深部开采中得到电阻率法测试结果的证实.李术才等[2]通过临界值定义，在淮南矿区丁集煤矿深部巷道围岩中通过钻孔电视成像仪观察到了分区破裂化.周小平等[3]运用弹性力学和断裂力学理论，研究了破裂区和非破裂区的宽度和数量问题.李英杰等[4]探讨了围岩分区破裂机理，认为它是劈裂破坏现象.李树忱等[5]通过对围岩或数值单元的破坏进行重新定义或改造后，利用FLAC3D的模拟获得围岩的分区破裂图像，并简要讨论了不同因素的影响程度.苏永华[6]等研究了原岩应力场对分层断裂的影响.

深部工程开挖和试验均观察到围岩的非经典破裂现象，但数值分析作为地下工程开挖一种最普遍的模拟手段，早先海量的模拟成果一直没有出现非经典破裂现象，而上述文献模拟结果虽然得到分区破裂，但对经典破裂定义进行了修正.所以有些专家一直困惑甚至怀疑[7]，如果围岩的非经典破裂是深部工程开挖围岩响应的特征，为什么常规的数值模拟中却观察不到？

本文根据深部工程围岩的赋存环境，分析了围岩的受力传递途径，根据其特征选用相应的模型刻画其力学特征.建立常规数值模型并在模拟中监控围岩各部分应力发展过程.利用监控资料，基于岩石力学破裂原理，分析深部围岩非经典断裂现象之一——分层断裂产生的机制，释疑深部围岩非经典破裂与数值模拟结果关系的困惑.

1 深部隧道围岩环境特点

有关工程测试及研究显示，达到一定深度的地层，原位应力场会趋于静水应力状态，岩体在高围压应力状态下会处于潜塑性状态.由于成岩后完整岩层在漫长历史中多次承受地质运动的扰动和破坏作用(开挖是其受到的最新扰动和破坏)，开挖在对围岩单侧卸载的同时弱化了岩体物理力学性质，使开挖面围岩复位变形导致处于静态的原生、次生裂隙复活，并萌生新的卸荷裂隙.图1是完整岩块中裂隙对于强度影响的试验过程结果[8]，图中上面实线为无连续面的岩体峰值强度，下面实线相当于岩石的残余强度.

图1 结构面倾角对岩石强度的影响

试验显示，当完整岩石中存在裂隙时，在绝大多数情况下会从岩石的峰值强度降低到残余强度.原有裂隙的复活和卸荷裂隙的萌生导致了深部工程围岩中大量各式裂隙的存在.所以深部地层岩体是完整地层的损伤体.深部工程围岩对开挖的力学响应行为应该是岩石峰后特征的表现.多位专家提出[7]，峰后岩石的应力-应变软化行为导致了分层断裂、分区破裂化等非典型破裂现象.

2 数值模型及计算方案

根据深部工程围岩的上述特征，在本部分选用能反应岩石峰后特征的应力-应变软化模型及相关参数，并设计相应模拟计算方案.在数值模拟中，作任何人为的假设和前提，完全遵循常规的开挖数值模拟原理和力学分析方法.

2.1 应力-应变软化模型

理想弹塑性模型如莫尔-库仑模型，在塑性屈服开始后，黏聚力、内摩擦角、剪胀角和抗拉强度等岩体参数均维持恒定值，而实际上岩体在破裂过程中由于裂隙的发展，上述性质会发生弱化.因此应力-应变软化模型引入了峰后参数的弱化特性，以反映岩体损伤局部化过程，表达裂隙的萌生、扩展及演化.FLAC3D软件内有成熟地描述岩石力学性质的模型，选用FLAC3D作为本项研究的模拟工具．软化模型在理想塑性模型基础上定义应变软化参数η，该参数可表示为：

(1)

2.2 数值模型

经典的弹塑性开挖分析结论，即隧道开挖后仅在靠近临空面围岩中形成单一的破裂区是在轴对称圆形断面中得到的.为了对照，相应地模拟计算中选用一半径为2 m的圆形隧道，模型外形范围尺寸为7倍隧道半径.按轴对称原理，计算模型采用半径为16 m的四分之一圆域，该模型被划分为51 798个单元，如图2所示.深部岩体初始应力为静水压力，模型的外圆弧为应力边界(考虑静水压力)，内圆弧为临空面，其余均为法向位移约束.

图2 数值计算模型

围岩力学参数参照湘西某穿越武陵山脉的公路隧道砂岩围岩力学参数：岩石剪切模量G=103MPa; 泊松比μ=0.25，峰值黏聚力cp=0.5 MPa，峰值摩擦角φp=30°; 残余黏聚力cr=0.35 MPa，残余摩擦角φr=22°; 岩体剪胀角ψ=3.75°，初始地应力为σ0=6 MPa.

2.3 计算及监测方案

图3 不同峰后脆性示意图

3 模拟结果及机制分析

根据上述方案进行了大量的模拟计算和围岩响应监测，获得了大批监测数据和相应图件，其中有关资料、结果如下.

3.1 分层断裂产生的条件

图4 圆形洞室围岩弹塑性应力场

单元离洞壁距离/m

单元离洞壁距离/m

在具体的工程实际中，有关学者在甘肃金川镍矿深部地下巷道围岩监测中发现了类似的现象[9]，监测得到的应力σ1在约5 m的地方出现应力低点，而在6 m处出现较明显的峰值.

3.2 分层断裂差异表现

图围岩断裂分布情况

图围岩断裂分布情况

根据上述围岩断裂分布情况可知：

1)岩石的峰后脆性影响着围岩分层断裂分布形态.随着峰后脆性的增强，分层断裂现象越来越明显.原因可能是峰后脆性的增强使岩石达到峰后残余阶段时仅需产生较小的塑性剪切应变.岩体在产生同样的塑性剪切应变值时，峰后脆性最强的岩体可能已经处于残余阶段，而其他岩体可能仍处于具有较大强度的软化初始阶段.峰后脆性越弱，其应力应变关系越接近理想弹塑性状态，由此造成了断裂形态上的区别.

2)随着峰后脆性的增强，分层断裂面向围岩深处延伸，分层断裂圈半径逐渐增大.这是由于峰后脆性的增强导致岩体将更有可能处于残余阶段，围岩强度的降低使其断裂层范围也增大.

图9～图12为水平方向和垂直方向围岩中径向应力σr和环向应力σθ的分布状况.

从图9～图12显示，围岩环向应力，径向应力分布曲线低应力→高应力→低应力→高应力反复交替出现.

单元离洞壁距离/m

单元离洞壁距离/m

单元离洞壁距离/m

单元离洞壁距离/m

3.3 分层断裂产生机理简析

深部地下工程开挖，对于靠近隧道临空面一定范围的围岩，相当于卸载径向力，同时由于应力转移和传递形成更高的环向应力.陈士林[10]等，王明洋[11]等，根据地下结构开挖应力重分布理论和支撑压力理论分析，从宏观上导出了深部工程开挖围岩的多重自由面应力模型．

多重自由面应力模型从理论上有效地解释了分区破裂化现象，但由于地下岩体的和工程本身的特点和复杂性，无法从试验中观察到，仍然存在质疑[7]：这种从理论上假设的自由面是否会真正形成，认为这种假设的真实性无法确认.至此，上述数值试验结果，图10，图11和图12等应力分布图，可以清晰地看到，隧道围岩中的次生自由面确实是存在的，为深部工程开挖围岩中的多自由面理论模型提供了数值试验验证.

对处于支承压力区的微单元体进行受力分析，此时可认为单元体径向应力σr和环向应力σθ均为主应力，且其环向应力σθ比初始围压大，而径向应力σr小于围压.微单元体相当于处于较大的主压力及较小的侧压力作用下的单轴压缩(如图13)，当主压力与侧压力满足一定条件时，单元体将发生劈裂破坏.Fairhurst等[12]研究指出，当应力值达到格里菲斯强度时，裂纹将向最大主应力方向扩展.对于圆形洞室，当应力状态满足一定关系时，围岩中的裂纹将沿着最大主应力方向发展，即围岩环向应力σθ方向.当应力足够大时，该裂纹将最终贯通，形成环状断裂，由此产生分层断裂现象的第一层断裂层.第一个断裂层相当于围岩中一个新的自由面，从而在围岩深处进一步形成峰值应力区和新的断裂层.如此反复，直至环向应力和径向应力不满足断裂发生的条件.

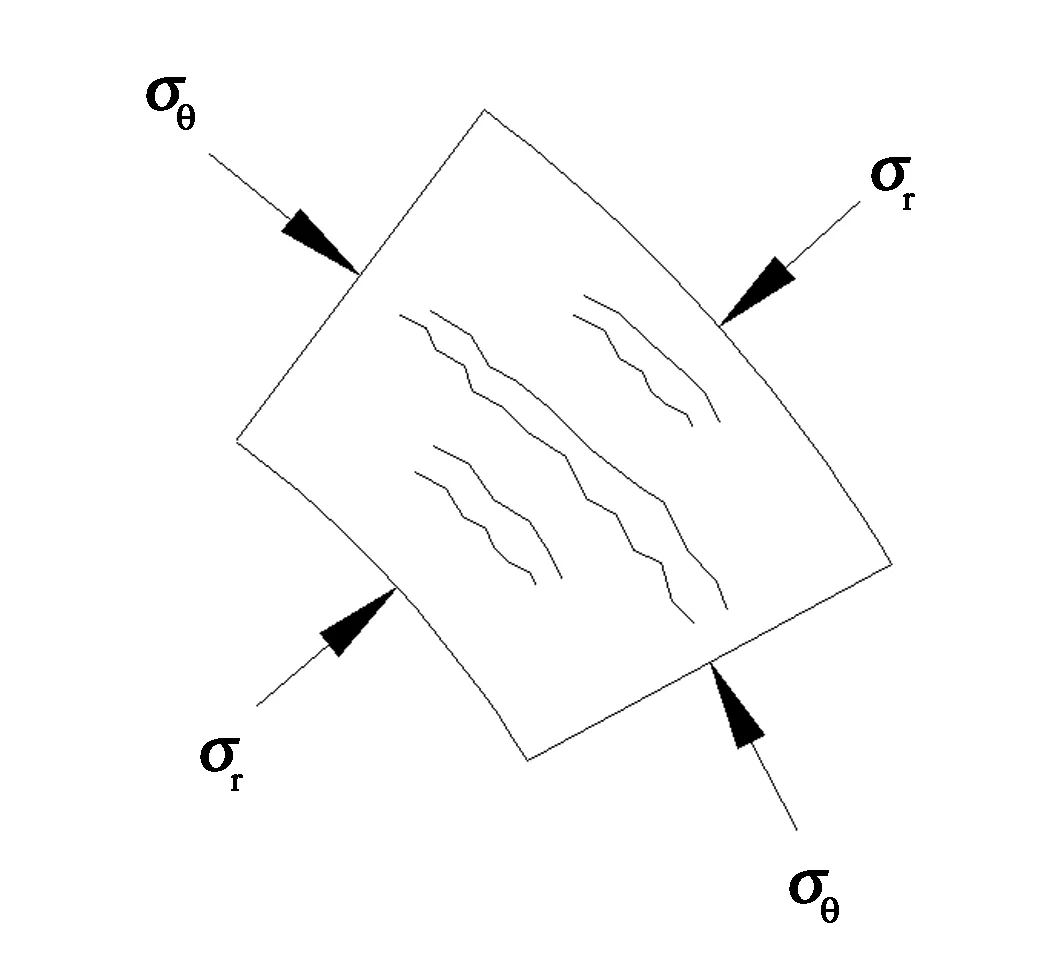
图13 峰值应力区的微单元体

表1 断裂层单元应力统计表

4 结 语

本文基于应变软化模型建立数值模型并监控围岩各部分应力发展过程，利用岩石力学破裂原理分析分层断裂产生的机理.在如下几个方面取得进展：

1)清晰地将深部工程开挖导致的围岩分层断裂现象在数值模拟中得到重现，为消除因数值模拟没有观察到分层断裂而导致对深部工程围岩非典型破裂现象的真实性和普遍性的疑虑提供了依据.

2)围岩中破裂区域径向应力、环向应力的强烈震荡性分布，证实了深部工程开挖围岩中多自由面理论模型的正确性.

3)岩石的峰后脆性是分层断裂的决定性因素之一.随着峰后脆性的增强，断裂层数增多、断裂层宽度和整个破裂带的范围、断裂层与完整带之间的应力降幅、应力峰值增大.

4)围岩中次生的环向应力和径向应力对分层断裂的扩展具有重要影响，两者应力比值满足一定条件时，将会产生环状断裂.

5)应变软化模型在一定程度上可以模拟深部岩体分层断裂现象.但本文的结果仅仅是初步的，模拟工具、方法，分层断裂机理的精确定量关系等，将是下一步需要大力推进的工作.

[1]SHEMYAKIN E I, FISENKO G L, KURLENYA M V,etal. Zonal disintegration of rocks around underground workings. Part 1: data of in-situ observations[J]. Soviet Mining Science, 1986,22(3): 157-168.

[2]李术才,王汉鹏,钱七虎,等. 深部巷道围岩分区破裂化现象现场监测研究[J]. 岩石力学与工程学报, 2008,27(8): 1545-1553.

LI Shu-cai, WANG Han-peng, QIAN Qi-hu,etal. In-situ monitoring research on zonal disintegration of surrounding rock mass in deep mine roadways[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(8): 1545-1553. (In Chinese)

[3]周小平,钱七虎. 深埋巷道分区破裂化机制[J]. 岩石力学与工程学报, 2007, 26(5): 877-885.

ZHOU Xiao-ping, QIAN Qi-hu. Zonal fracturing mechanism in deep tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2007,26(5): 877-885. (In Chinese)

[4]李英杰,潘一山,李忠华, 等. 岩体产生分区碎裂化现象机理分析[J].岩土工程学报, 2006, 28(9): 1124-1128.

LI Ying-jie, PAN Yi-shan, LI Zhong-hua,etal. Analysis of mechanism of zonal disintegration of rocks[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9): 1124-1128. (In Chinese)

[5]李树忱,冯现大,李术才，等. 深部岩体分区破裂化现象数值模拟[J]. 岩石力学与工程学报,2011,30(7): 1337-1344.

LI Shu-chen, FENG Xian-da, LI Shu-cai,etal. Numerical simulation of zonal disintegration for deep rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2011,30(7): 1337-1344. (In Chinese)

[6]苏永华,郑璇. 深部节理岩体分区破裂化机制数值研究[J]. 公路交通科技,2013,30(1): 94-101.

SU Yong-hua, ZHENG Xuan. Numerical study on mechanism of zonal disintegration in deep rock mass with joints[J]. Journal of Highway and Transportation Research and Development, 2013,30(1): 94-101. (In Chinese)

[7]中国科学技术协会. 围岩分区破裂现象以及相关的理论问题报告[R]. 北京:中国科学技术协会,2008:47-50.

China Association for Science and Technology. Reports of zonal disintegration phenomenon and related problems in deep roadways[R]. Beijing: China Association for Science and Technology, 2008:47-50. (In Chinese)

[8]李志业,曾艳华. 地下结构设计原理和方法[M]. 成都: 西南交通大学出版社,2009：32-33.

LI Zhi-ye, ZENG Yan-hua. Design principle and method of underground structures[M]. Chengdu: Southwest Jiaotong University Press, 2009：32-33. (In Chinese)

[9]刘高,王小春,聂德新. 金川矿区地下巷道围岩应力场特征及演化机制[J]. 地质灾害与环境保护, 2002,13(4): 40-45.

LIU Gao, WANG Xiao-chun, NIE De-xin. The characteristics and evolution mechanism of stresses in surrounding rocks of underground works in Jinchuan mine[J]. Journal of Geological Hazards and Environment Preservation, 2002, 13(4): 40-45. (In Chinese)

[10]陈士林,钱七虎,王明洋. 深部坑道围岩的变形与承载能力问题[J].岩石力学与工程学报, 2005, 24(13): 2203-2211.

CHEN Shi-lin, QIAN Qi-hu, WANG Ming-yang. Problems of deformation and bearing capacity of rock mass around deep buried tunnels[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(13): 2203-2211. (In Chinese)

[11]王明洋,宋华,郑大亮，等. 深部巷道围岩的分区破裂机制及“深部”界定探讨[J]. 岩石力学与工程学报, 2006, 25(9):1771-1776.

WANG Ming-yang, SONG Hua, ZHENG Da-liang,etal. On mechanism of zonal disintegration within rock mass around deep tunnel and definition of “deep rock engineering”[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(9): 1771-1776.(In Chinese)

[12]FAIRHURST C, COOK N G W. The phenomenon of rock splitting parallel to the direction of maximum compression in the neighborhood of a surface[C]//Proceedings First International Congress. Lisbon:International Society for Rock Mechanics,1966: 687-692.