关于平衡态热力学常见过程的定义

郭余年 程铁欣

(1长春工业大学 吉林长春130012;2吉林大学化学学院 吉林长春130021)

平衡态热力学所研究的是处于平衡态的封闭系统及其由一个平衡态变为另一个平衡态的过程。平衡态热力学中的常见过程指的是等温过程、等压过程和等容过程。

1 等温过程定义

1.1 等温过程定义的说法

关于等温过程的定义，存在着不同的说法。主要有以下3种:

说法1 系统的始态温度T1等于终态温度T2等于环境的恒定温度T环(恒定)的过程为等温过程［1-5］，即:

式中的“定值”不宜写为“常数”，因为T不是量纲指数为0的纯数。

说法2 系统与环境的温度相等并恒定不变的过程为等温过程［6-10］，定义式为:

式(2)中的T是所谓“过程中系统的温度”。

说法3 其他说法。该说法是通过种种努力将说法1与说法2“统一”起来的说法，统称为其他说法。由于说法1与说法2有差别，所以这些努力为等温过程定义这个概念平添了一些混乱。

比较式(1)与式(2)知，这两种说法都认为等温过程是环境温度恒定的过程，这是它们的共同点。由于过程中系统的温度T恒定，自然满足T1=T2，故说法1包括了说法2。但是，满足T1=T2可能有两种情况:一是过程中系统的温度不恒定;一是恒定。即说法2是说法1的两种可能情况之一，这是它们的差别。由于这个差别，它们描述的过程不完全相同。

1.2 等温过程一例

等温过程常见的实例是将具有透热壁的系统放在与它始态温度相同的一个热源中进行的过程。

设有一活塞筒是透热壁，活塞无质量且与筒壁无摩擦，筒内充有物质的量为n，压力为p1，体积为V1，温度为T的理想气体。把它放在温度为T的热源(T环=定值)中。使气体变为压力为体积为V2，温度为T的终态。气体的该过程示意如下:

若以下面3种途径完成这一过程:

(a)气体恒外压一次膨胀;

(b)气体分3步恒外压膨胀(三次膨胀);

(c)气体在与环境的压差为无限小的情况下连续地膨胀(准静态膨胀)。

这3种途径组成的过程都是等温过程，它们的共性是都满足式(1)。即说法1与此例相符;途径(a)和途径(b)是等温不可逆过程，在不可逆过程中，系统必经历非平衡态，因而，系统在不可逆过程中不可能存在均匀的温度。例如，活塞筒内的气体膨胀时，气体各部分的密度、温度和压力并不完全相同，靠近活塞表面的气体的密度要小些，温度和压力要低些;说法2与此不符，说法1对此并不排斥。途径(c)是等温可逆过程，在过程进行中，系统时刻处于(或无限接近于)平衡态，因而有一个与环境恒定温度相等的温度T，即T=T环=定值，此式即是式(2);亦即，说法2与此相符，说法1对此也可包容。所以，说法1作为等温过程的定义是可取的;说法2定义的过程是等温可逆过程，把它作为包括不可逆和可逆两种情况的等温过程的定义是不全面的。

对于此例(或类似此例)中的热源的作用，也存在着不同的提法:提法①“以保持系统为恒温”［11-13］;提法②“以使平衡时系统的温度与热源的温度相等”［9］;提法③“以维持气体的温度”［1］。

作为系统的环境的热源，是以地球、大气、海洋等实际物体为背景抽象出来的理想化的客体，它应是物质的量与热容为无限大的客体，它不因有限热量的得失而变温。因而为过程的进行提供一个恒温环境(T环=定值)。在平衡态热力学中，系统(或环境)过程的始态和终态都是平衡态［2］。在不存在绝热壁的情况下，热源的作用之一就是约束系统的始态及终态温度与环境的恒定温度相等。根据热力学第零定律，温度是描述系统平衡态的一个物理量;对于非平衡态系统，不能用温度来描述它的状态。所以，关于等温过程中热源的作用，提法①是不符合实际、不正确的，但它却支持了等温过程定义的说法2的观点;提法②和提法③都是正确的。显然，提法③比提法②简练，但它易被误解。

1.3 说法2定义的过程是等温可逆过程

温度是热力学第零定律揭示出来的均相系统的一个平衡性质，并表述为温度定理:“任一热力学均相系统，在平衡态各自都存在一个状态函数，称之为温度(T);它具有这样的特性，对于一切互呈热平衡的均相系统，其温度彼此相等。”［14］将说法2与该定理对照有:① 在说法2定义的过程进行中，系统应时刻处于平衡态。根据过程进行中系统是处于平衡态还是非平衡态，将过程分为准静态过程和非准静态过程两大类。非准静态过程就是不可逆过程。因此，说法2定义的过程肯定不是(或不包括)不可逆过程，而只可能是准静态过程;②在说法2定义的过程进行中，系统与环境应时刻处于热平衡状态。对于有传热的过程，系统与环境处于热平衡状态下的热传导，叫做“等温热传导”。无摩擦的、系统与环境进行等温热传导的准静态过程(如上例中的途径(c))是可逆过程。

在任一封闭系统的一个微变过程的Clausius不等式

中:＞适用于不可逆过程，=适用于可逆过程(下同);δQ是实际过程中系统与环境交换的热量;T环(恒定)是环境的温度，因为环境是热源，在过程中其温度恒定，记作T环(恒定);dS是过程中系统的熵变，其定义为:

式(4)中，δQr是过程可逆时系统与环境交换的热量;T是系统的温度。

假设该微变过程是可逆过程，式(3)中的δQ变为δQr且式(3)只取等号。有:

对于有传热的过程，δQr≠0，则由式(5)有:

此式即是式(2)。从普适的式(3)至式(2)只附加了一个“可逆过程”的条件，即只有当过程是可逆时，过程中系统的温度才等于环境的恒定温度。亦即，说法2定义的过程是环境温度恒定条件下的可逆过程。所以，说法2定义的过程是说法1定义的过程的可逆情况。如果把说法1定义的过程叫做等温过程，则说法2定义的过程就是等温可逆过程(或恒温过程)。

1.4 定义的应用与检验

等温过程定义的应用之一是在由判断过程方向、限度的熵判据引出Helmholtz函数判据的演绎中，应用说法1进行该演绎可有多种方法:

方法＜1＞ 对于任一均相系统的任一有限过程，式(3)变为:(5)

若过程中环境对系统做的总功为 W;系统的热力学能(U)的增量为 ΔU，由热力学第一定律(ΔU=Q+W)，有:

式中ΔU≡U2-U1，ΔS≡S2-S1，若过程为说法1定义的等温过程，则由式(1)，有:

代入式(7)，有:

将均相平衡态系统的状态函数(U-TS)称为Helmholtz函数(A)，即:

式(9)适用于均相平衡态系统。将式(9)代入式(8)，有:

外推得:

式(10)和式(11)即为Helmholtz函数判据;下标T表示此2式适用于说法1定义的等温过程，因为在由式(6)至此2式的演绎中应用了式(1)。

应用说法1进行熵判据至式(10)的过渡简便且直观，物理意义清楚，结果正确。那么可否应用说法1从熵判据直接得到式(11)呢?有人认为不可能，因为说法1是针对有限过程定义的;只有说法2才能解决这个问题，因为它是对无限小过程进行定义的。其实不然。

方法＜2＞ 对均相系统的任一微变过程，式(7)变为:

对于等温过程，由式(1)，有:

即:

即:

将式(9)代入式(15)，得式(11);外推得式(10)。

方法＜3＞ 由于在等温过程定义的说法1中，系统的始态、终态以及环境(热源)的温度是任意指定的。若该温度指定为T(如上例)，则由式(1)，有:

在式(16)中，T是系统任一平衡态的温度。由式(16)，有:

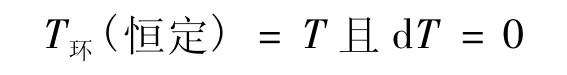
则:

代入式(12)得式(15)，经式(9)得式(11);外推得式(10)。

2 等压过程定义

对于等压过程的定义，也有与等温过程定义类似的各种说法:

说法1 系统始态压力p1等于终态压力p2等于环境的恒定压力p环(恒定)，即:

的过程为等压过程［2-5］。

说法2 系统与环境的压力相等并恒定不变的过程为等压过程［6-9］，其表达式为:

式(18)中的p是所谓“过程中系统的压力”。

说法3 其他说法。该说法是通过各种努力将说法1与说法2“统一”起来的说法，统称为其他说法。由于说法1与说法2有差别，所以这些努力为等压过程定义这个概念带来了一些混乱。

压力(p)只在系统的平衡态中才有明确的意义，系统在非平衡态时不存在均匀统一的压力。因此，说法2定义的过程是说法1定义的过程的准静态过程。如果把说法1定义的过程叫做等压过程，则说法2定义的过程是等压准静态过程或进一步理想化的等压可逆过程(或恒压过程)。所以，将说法2作为等压过程的定义是不合适的。

等压过程定义的应用之一是在引出Gibbs函数判据的演绎中，并在演绎中接受检验。应用说法1进行该演绎可有以下方法:

方法＜1＞ 将过程的总功W分为体积功W体和非体积功W'。由体积功的定义(δW体=－p环dV)知，对于式(17)定义的等压过程，有:

对等温等压过程，由式(10)与式(19)，有:

定义平衡态均相系统的状态函数(A+pV)为系统的Gibbs函数(G)，即:

式(21)适用于平衡态均相系统。将式(21)代入式(20)，有:

或:

在式(22)与式(23)中，下标T，p表示此2式适用于式(1)和式(17)定义的等温等压过程，此2式即是Gibbs函数判据。

方法＜2＞ 对均相系统等温等压微变过程，式(11)可改写为:

由式(17)，有:

即:

即:

将式(21)代入式(27)得式(23);外推得式(22)。

方法＜3＞ 等压过程常见的实例是在不存在刚壁的情况下，将系统放在与它始态压力相同的一个恒压环境(p环=定值)中进行的过程。若指定任一平衡态均相系统的压力为p的状态为始态，即p=p1，则对由式(17)定义的等压过程，有:

形似式(18)的式(28)中的p为任一平衡态均相系统的压力。由式(28)，有:

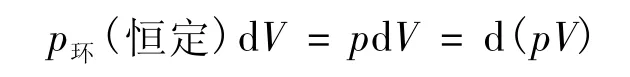
代入式(24)，经式 (21)得式(23);外推得式(22)。

3 等容过程定义

对等容过程的定义，也存在着不同的说法。主要有:

说法1 系统体积V恒定不变，即:

的过程为等容过程。

说法2 系统的始态与终态体积相等，即:

的过程为等容过程。

说法3 说法3是将说法1与说法2放在一起的说法。例如有的给出了定义式“V=V1=V2=定值”。

虽然对定义有不同的说法，但在应用中各种说法的作者都采用的是说法1，即等容过程就是系统的体积恒定不变的过程。等容过程一般是指在刚性密闭容器中或凝聚系统发生的过程。

4 小结

系统与环境的温度(或压力)相等并恒定的过程，是等温(或等压)过程极限情况的可逆过程，关于可逆过程的实质，有一句名言:“在寻常的实验时间里，可逆过程等于没有过程，也就是平衡状态。”［16］

［1］傅鹰.化学热力学导论.北京:科学出版社，1963

［2］吉林工业大学，吉林工学院.物理化学.北京:机械工业出版社，1980

［3］王明德.大学化学，2011，26(4):72

［4］朱文涛.基础物理化学(上册).北京:清华大学出版社，2011

［5］杨永华.物理化学.北京:高等教育出版社，2012

［6］胡英.物理化学(上册).北京:人民教育出版社，1979

［7］胡英.物理化学(上册).第3版.北京:高等教育出版社，1988

［8］胡英.物理化学(上册).第5版.北京:高等教育出版社，2007

［9］天津大学物理化学教研室.物理化学(上册).第4版.北京:高等教育出版社，2001

［10］朱志昂，阮文娟.近代物理化学(上册).第4版.北京:科学出版社，2008

［11］傅献彩，沈文霞，姚天扬，等.物理化学(上册).第5版.北京:高等教育出版社，2005

［12］傅献彩，陈瑞华.物理化学(上册).第3版.北京:高等教育出版社，1979

［13］傅献彩，沈文霞，姚天扬.物理化学(上册).第4版.北京:高等教育出版社，1990

［14］韩德刚，高执棣，高盘良.物理化学.第2版.北京:高等教育出版社，2009

［15］沈文霞.物理化学核心教程.第2版.北京:科学出版社，2009

［16］黄子卿.物理化学.北京:高等教育出版社，1955