高速8PSK的PFD载波恢复设计

吴文权，姚远程，秦明伟

(1.西南科技大学信息工程学院，四川绵阳 621010;2.特殊环境机器人四川省重点实验室，四川绵阳 621010)

MPSK调制方案广泛应用于一些高速的数字无线通信系统中，如宽带数字视频广播系统、中继卫星通信系统等，具有频谱利用率高和较强的抗干扰能力。载波同步是通信中的一个重要问题，它关系着整个通信系统的质量。无线通信中由于多普勒平移以及较高的符号率等原因，往往存在着较大的频偏，对于高阶的PSK调制中载波恢复，同时也要求具有较小的稳态相差来抵抗较低的信噪比。高速8PSK调制的载波同步方案的设计目标:能够捕获和跟踪较大的频偏，具有较小的稳态相位抖动，长时间稳定性好，易于硬件实现。

对于8PSK的载波同步，如采用一些数字锁相环，如科斯塔斯环路、松尾环等用于QPSK的同步环路(costas环)，由于其部分星座点的两路幅度不同，需要对costas环路和松尾环做一些修改才能用于8PSK［1］。文献［2］提出了一种用于MPSK的基于DFT的盲频率捕获的方法，具有较好的性能。文献［3］中提出一种使用MQAM和MPSK信号的通用载波同步环路，理论上能够完全消除码型噪声和避免其他算法跟踪高阶调制方式出现的假锁点，能够达到比较理想的载波跟踪，但这种方式随着调制阶数的升高，环路线性捕捉范围将会迅速减少，不适于大频偏的捕获。本文结合通用载波同步环路的优点，设计了适合于高速8PSK大频偏捕获的PFD环路，克服了通用环路捕获范围小的缺点，同时能够得到比较小的稳态相差，而且环路结构简单，易于硬件实现。

1 环路设计

基于8PSK的PFD载波恢复环路设计整体框图如图1所示。其中S(t)为混频后经过低通滤波器的，已经完成了定时恢复，包含有相偏和频偏的基带信号。NCO反馈回来的正余弦信号经过基带的解旋后，通过CORDIC算法计算出信号星座点的相位角，这里相位角有两个作用，一是用来做通用环路的预判决信号，二是作为PFD的加窗信号。当星座点落入到某个范围内，进行相位跟踪，如果在该范围之外，就保持上个时刻的鉴相输出，使得环路具有鉴频鉴相的功能。得到的误差信号通过环路滤波器输出控制NCO的归一化误差，NCO输出的正余弦通过解旋模块，去除基带信号的相偏和频偏，得到正确的解调信号。

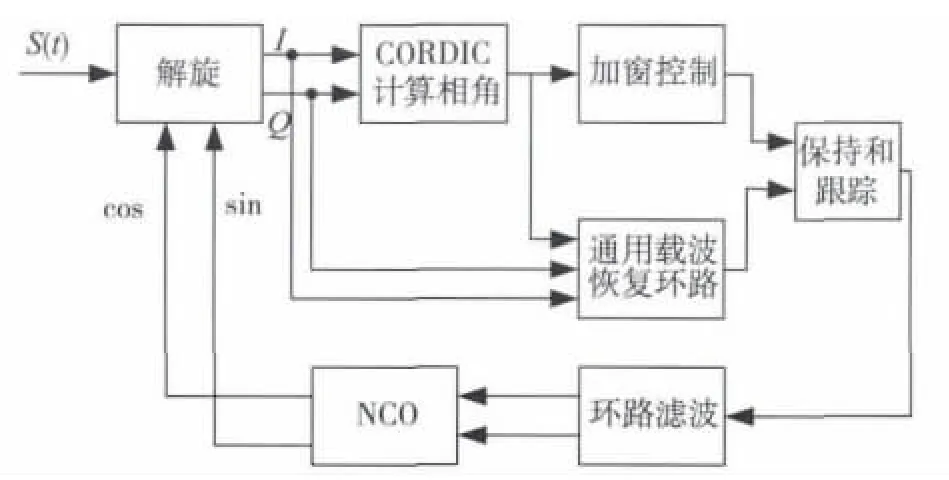
图1 PFD载波恢复环路

2 各模块设计

2.1 解旋模块

相位解旋一般有两种方法，正交下变频方案和复数对相位解旋方案。正交下变频方案要将误差信号反馈到中频去混频，复数对相位解旋方案为反馈到近似零中频包含有频偏的信号中，是一种基带解旋处理，为了降低载波同步模块的处理速率，文中采用第二种方案。复数对相位解旋实现框图如图2所示。

图2 复数对相位解旋框图

其解旋原理如下:正交调制中经过下变频和低通滤波后含有频偏的I，Q两路信号为

式中:Δω为频率偏差。这里假设NCO输出为经过跟踪、达到系统频偏频率的正余弦信号，即输出为sin(Δωt)和cos(Δωt)。则根据图2的解旋原理，解旋输出为

将式(1)、式(2)代入到式(3)、式(4)可以得到

由式(5)可以知道，当环路跟踪，使NCO的输出与输入的信号达到了严格的同频同相之后，通过解旋模块后，得到需要的两路基带信号，完成了解旋。

2.2 鉴相算法模块设计

通用载波同步环是一种专门用于QAM信号集的载波恢复环路，它同样也是适用于MPSK信号。通用环在高阶调制的同步中，不需要改变其鉴相算法部分，而只需根据不同的调制方式来设计不同的判决模块，适合于具有多种正交调制方式的接收机［4］。同时，通用环锁定时相位抖动小，这里选通用环作为鉴相算法，其实现结构框图如图3所示。

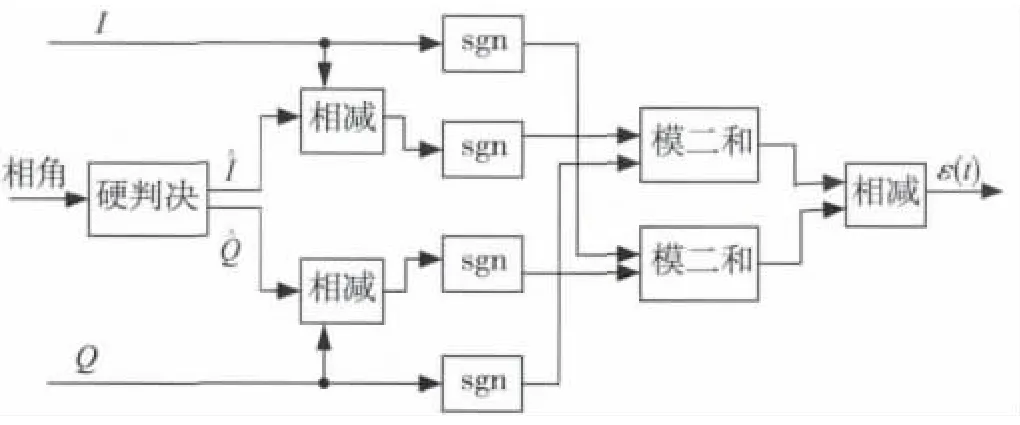
图3 PD设计框图

由结构图可知通用环的鉴相特性函数为

式中:I，Q为解旋后的基带信号，为硬判决后的输出。判决规则是星座点的相角［5］，以两个星座点的中间分界为判决界限，如调制到0的8PSK信号，将星座点分为8个区间，如将落入到－π/8～+π/8的星座点判决为=1=0，其他角度的判决类似。

2.3 PFD模块

由Sari等人提出的PFD算法［6］，其原理是基于传统PD基础上，进行了一些改动，只增加一部分的判断控制模块，使得PD算法又具有FD的功能，从而来弥补PD不具有鉴频的缺点。PFD模块设计的框图如图4所示。PFD的工作原理为，一般PD的输出为零直流分量信号，这样的信号是无法提供频偏信息的，因此在环路中加入了一个判断和保持的模块，这里一般采用对星座点加窗的方法，来判断星座点是否落在了窗内，如果落在了窗内，则输出PD，如果不在窗内，则保持上一个鉴相误差的输出，这时输出一个跟频偏具有相同的极性直流分量，此时环路具有FD的功能，直到下一个检测周期，再次来检测星座点的位置。

图4 PFD控制模块设计框图

根据图4可以得到PFD的输出为

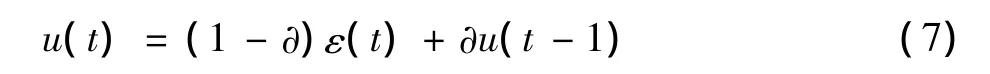
式中:∂根据检测星座点是否落在窗内取0和1;ε(t)为鉴相输出。

星座点加窗的思想来源于文献［7－8］，不同的调制方式有不同的加窗方法，如对QPSK调试方式，文献［9］提出采用星座点的横纵坐标来判断是否落在窗内，而对于QAM信号的加窗一般采用幅度来判断。对于8PSK窗的设计，这里提出2种加窗方法:

1)根据星座点的圆周幅度。设置一个角度θ为界，判断某一星座点，找出与其距离最近的一个标准星座点，然后计算出这个星座点与标准星座点之间的圆周幅度是否为θ，当小于θ时，则表明落在了窗内，否则落在了窗外。

2)根据星座点的相角。计算出星座点的相位角，同样设置一个角度θ，然后用标准星座点的相位角加减θ为窗，如果这个星座点的相角小于θ，则表明在窗内，否则在窗外。

比较以上2种加窗设置门限的方法，第2个方法是要优于第1个方法，因为第1个方法容易受到噪声的影响，如果受到噪声的影响，星座点不再落在标准圆上，此时，求出的圆周幅度不再准确，会造成门限的误判，影响其收敛的速度。使用第2个方法的另外的一个原因是判决时正好已经求出了星座点的相位角，可以直接用相位角来判断星座点是否落在窗内。设计的PFD门限示意图如图5所示，黑点为标准的星座点，θ为门限的界，两虚线之间的部分为窗口，对每个星座点都如此设置，因此总共有8个窗口。

图5 PFD的星座窗口门限示意图

对于门限值θ的选择，要遵循一些规则，对于8PSK调制方式，门限值不能大于π/6，因为如果大于π/6，会造成相邻两个窗口的混叠和干扰，造成窗口不能正常工作。在没有噪声下，检测的直接增益满足

式中:θ为窗口界限;g(·)为PD输出。从式(8)可以看出，对于小的窗口可以获得大的直流增益，能够捕获更大的频偏，但同时，小窗口的抗噪声性能很差，因此对于窗口大小要在频偏捕获范围和抗噪性能上折中选择，文中选用π/12作为窗口界限。

2.4 环路滤波器

这里的LF(环路滤波器)采用常用的二阶型，环路滤波器具有平滑输出误差、滤除误差中的高频成分和噪声的作用，它的输出控制数控振荡器的频率控制字，由此来改变数控振荡器的输出频率，不断拉动NCO的输出频率向发送的载波频率靠近，误差在一个极小的范围内波动，使环路达到稳定。二阶环路滤波器的参数计算式［10］为

式中:wn为自然角频率;ts为采样周期;ξ为阻尼因子，工程上取值一般为0.5～0.707，这里取0.707。根据实际的需要设定等效噪声带宽Bn，Bn与自然角频率和阻尼因子的关系为

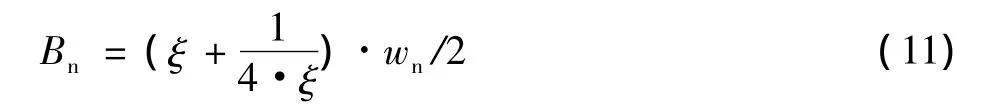
根据以上公式，就可以计算出环路滤波器的参数C1，C2。

3 仿真结果分析

根据以上各部分的设计，按照图1的总体框图，采用MATLAB/Simulink软件搭建仿真模型，仿真的调制方式为偏移0°的8PSK调制。系统参数设置为，符号率Rb=40 Mbaud，滚降系数为0.35，对每个符号做4倍的插值。设置10 kHz的频偏后，控制信号∂的输出曲线如图6所示，由图可知，控制信号1 100个采样点之前，输出的为0和1交替的信号，表明窗口一直检测到没有在窗口中的点，此时处于FD工作状态，而且其所占的宽度不一样，开始时1和0的宽度差不多，表明落在窗口内和窗口外的点差别不大，1的宽度越来越宽，表明大频偏不断地被纠正，前后的频差越来越小，使得星座点旋转变慢，此时∂=1，到1 100点之后，∂的值一直保持在0，表明星座点全部落入到窗口之中，此时，环路进入PD的工作状态。

图6 控制信号∂的输出曲线

星座图的输出如图7所示，图7a为载波未同步的星座图，一直处于旋转状态，图7b为同步之后的星座图。

图7 载波回复前后的星座图

对系统加入400 kHz的频偏，即1/100符号率的频偏时，如果不加入FD控制环路，只是PD单独工作，LF输出如图8a所示，从图中可以知道，大概经过60 000个点后，环路跟踪上了频偏，纵坐标输出一直在0.01上下波动，即表示跟踪到的频率为0.01倍符号率。当加入FD控制环路后，LF的输出如图8b所示，从图中可以看出，大概经过20 000个点后，环路就跟踪上了频偏，通过两个图比较可以得出，加入FD工作后，环路的捕获速度提高了大概3倍。经过实测，PD工作的环路最多能够捕获到2%符号率左右的频偏，而加入FD控制环路后，可以捕获10%符号率的频偏。可以知道，设计的环路不但增大了捕获频偏的范围，而且也加快了其捕获速度，最后环路工作在PD下，稳态相位波动也比较小。

误码率曲线如图9所示，仿真了加入不同频偏时，系统纠正频偏的误码率性能。从图中可以看出，频偏较大时，误码率性能会下降，在较低的信噪比，如低于6 dB时，误码率恶化得比较多，大概2～3 dB，较高性噪比下，误码率曲线和理论只相差0.5 dB，说明频偏纠正模块具有较好的性能。

图8 LF的输出

图9 误码率曲线

4 结论

文中设计了基于8PSK的PFD载波恢复方案，分析了各部分的设计框图以及原理，通过仿真验证了PFD载波恢复模块相比于PD能够纠正较大的频偏、较快的捕获速度，PFD模块最后工作在PD下，载波恢复后也能获得小的相位误差抖动，通过对误码率曲线的仿真，得出该方案具有较理想的性能。

:

［1］张欣.扩频通信数字基带信号处理算法及其VLSI实现［M］.北京:科学出版社，2004.

［2］YAN Xiao，WANG Qian，QIN Kaiyu.Frequency pre－estimation aided carrier recovery algorithm for hign－speed M－PSK communication［C］//Proc.11th IEEE Singapore International Conference on Communication Systems.Guangzhou，China:IEEE Press，2008:1339－1343.

［3］LECLERT A，VANDAMME P.Universal carrier recovery loop for QASK and PSK signal sets［J］.IEEE Trans.Communications，1983，31(1):130－136.

［4］FILIP M，PANG K H.Simulation of a universal base－band carrier recovery loop［C］//Proc.IEEE Colloquium on New Synchronization Techniques for Radio Systems.London:IEEE Press，1995:1－6.

［5］徐光明，王世练，朱江，等.通用载波同步模块的设计与实现［J］.电子工程师，2008，34(8):25－27.

［6］SARI H，MORIDI S.New phase and frequency detector For carrier recovery in PSK and QAM systems［J］.IEEE Trans.Communications，1988，36(9):1035－1043.

［7］HORIKAWA I，MURASE T，SAITO Y.Design and performance of a 200Mbit/s 16QAM digital radio system［J］.IEEE Trans.Communications，1979，27(12):1953－1958.

［8］HORIKAWA I，SAITO Y.16QAM carrier recovery with selective gated phase－locked loop［J］.Electronics and Communications in Japan，1980，63(7):692－699.

［9］晏辉，张培忠.低信噪比下锁频锁相器性能分析及改进［J］.电子学报，2011，39(1):1－6.

［10］张安安，杜勇，韩方景.全数字Costas环在FPGA上的设计与实现［J］.电子工程师，2006，32(1):18－20.