采用入侵杂草优化算法的WSN定位精度提高方法
张 浩,吕 真,连卫民,王 硕
(河南牧业经济学院计算机系,河南郑州 450044)
无线传感器网络(Wireless Sensor Network,WSN)作为一种全新的信息获取和处理技术在众多领域具有十分广泛的应用前景[1]。同时无线传感器网络中的节点定位技术作为传感器网络众多应用的前提具有重大的支撑作用[2]。无需测距的定位算法作为一种典型的定位算法,因其在成本、功耗及环境定位精度方面的较强优势,而在大型WSN中备受关注[3]。DV-Hop算法作为无需测距定位算法的典型代表而成为这一领域的研究热点[4]。
众多学者在对DV-Hop算法的研究中指出,为了满足应用需求,需要进一步对该算法的定位精度进行提高。针对这一问题,文献[5-8]提出了一些改进方法:文献[5]将RSSI策略应用到在DV-Hop算法中计算节点间的距离上,利用减小节点间误差来对算法的定位精度进行提高;文献[6]通过在每步DV-Hop操作中引入介质访问机制来调节距离误差;文献[7]通过利用人工蜂群算法替代三边法计算未知节点的坐标改善了算法的定位性能;文献[8]通过引入最佳调整因子对每个锚节点计算的距离进行修正从而减小了平均跳距的计算误差。
本文受到文献[7]的启发,在详细介绍DV-Hop算法原理的基础上,通过对该算法产生误差的主要原因进行分析,将对未知节点坐标的计算转化为最优化求解,同时,通过确定目标函数,成功地引入了改进后的入侵杂草优化算法来计算未知节点坐标,使得锚节点与未知节点之间的距离误差大大减小,从而有效地提高了算法的定位精度。
1 DV-Hop算法描述
DV-Hop算法的主体由3个步骤组成,具体如下:
1)每个锚节点向处于通信范围内的邻居节点发出广播,通告其自身的位置信息。接收广播的节点收到数据后记录锚节点的最小跳数,同时对来自同一个锚节点的跳数信息中较大的进行忽略,然后将此跳数值加1后再向邻居节点进行转发。
2)每个锚节点根据所记录的其他锚节点的坐标信息和跳数,网络平均跳距估算公式为

式中:hopSij为锚节点i和j之间的跳数;(xi,yi)为锚节点坐标。
锚节点计算平均跳距后,对整个网络进行广播,未知节点收到平均跳距后,仅记录第一个收到的数值,然后转发给邻居节点;未知节点计算出平均跳距和跳数信息后,根据此数据估算出某个锚节点到未知节点i的距离,即

3)未知节点通过三边法或多边法计算未知节点的坐标,式(2)中Li计算公式为

式中:(xi,yi)为该未知节点所记录的锚节点的坐标;(x,y)为未知节点的坐标。通过整理后可以得到一个线性方程AX=b,其中
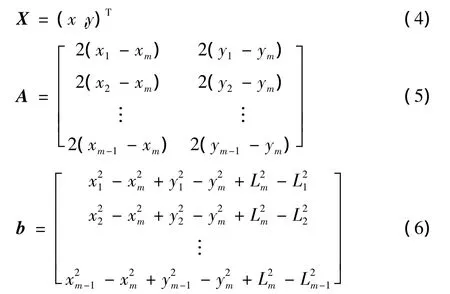
考虑到WSN中各种因素的影响,DV-Hop算法所测量的距离L必然存在较大误差,因此求解未知节点坐标的线性方程应为

式中:ε为误差向量。因此,对式(7)利用最小二乘法求解时由于误差向量ε的影响,使计算出的节点位置会产生较大的误差。针对这一问题,本文利用最优化方法通过确定目标函数将上述问题转化为最优求解问题,以期减小节点坐标的计算误差。
假设fn为未知节点到锚节点之间的测距误差,则
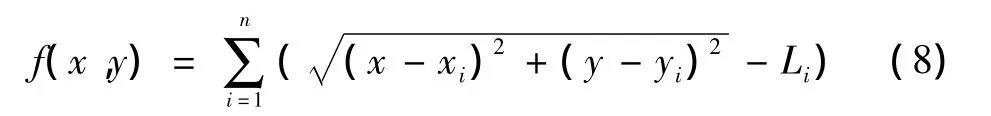
当式(8)要求总误差最小时,需取得最小值,且未知节点的解是最优的。而此时的最优解为坐标(x,y)满足

然而利用传统的数学方法求解上述方程存在不小的难度,而用来解决最优化问题中比较有效的方法之一就是利用入侵杂草优化算法[9]。综上所述,本文令式(9)为IWO算法的目标函数,从而成功地将未知节点坐标求解问题转化为非线性最优化问题,实现未知节点坐标的精度计算。
2 改进DV-Hop算法
2.1 入侵杂草优化算法
入侵杂草优化(Invasive Weed Optimization,IWO)算法[9]是模拟自然界中杂草群在空间中扩散、生长、繁殖和生存竞争过程的进化寻优算法,其中种群是所有杂草的集合,杂草为问题的可行解,种子是杂草产生的后代。IWO算法主要由3步组成:
1)杂草繁殖。随机产生的杂草根据其繁殖能力(适应度值)产生种子,即

式中:wi是种子个数;f(xi)是杂草xi的适应度值,xi(i=1,2,…,N)是D维杂草;fmin和fmax是当前种群中所对应的最小和最大适应度值;smin和smax分别是一个杂草所能产生种子的最小和最大个数。
2)空间扩散。在每个杂草的周围,按式(10)计算的种子个数产生种子,其中种子服从N(0,σ)的正态分布,σ的计算公式为

式中:σinitial和σfinal是标准偏差的最初值和最终值;itermax是最大进化代数;iter是当前进化代数;n为非线性调和因子,一般情况下n=3。
3)个体竞争生存。当种群规模大于最大种群规模P_Max后,种群中杂草和种子按适应度值大小进行排序,选取较好的前P_Max,淘汰其余个体。
2.2 基于蜂群搜索机制的IWO算法
在IWO算法的进化后期,随着进化代数的逐渐增加,种群多样性将逐渐降低,导致搜索空间缩小,从而使算法容易陷入局部最优。但是该算法并没有跳出局部最优的策略,因而容易出现早熟的现象。
Karaboga于2003年提出的人工蜂群算法[10]是一种群集智能优化算法。由于该算法的蜜源搜索方程针对蜂群的分工机制采用不同的搜索策略,因而其具有较强的探索能力,蜜源搜索方程为

式中:i,k={1,2,…,N},且i≠k,j={1,2,…,D}。φi,j为[-1,1]之间的随机数。从式(12)可以看出,新的候选解向种群中随机的个体移动,因而具有较强的随机性。然而该方程侧重于提高算法的探索能力,而忽略了算法的开发能力,针对这一问题,文献[11]结合粒子群算法的搜索方程,提出了全局最优引导策略,即
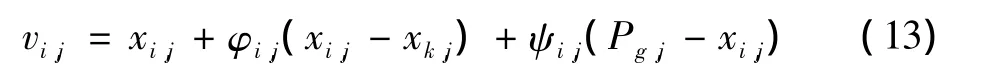
式中:Pg,j为全局最优解;ψi,j为[0,1.5]的随机数。通过这一策略有效地平衡了蜂群算法的开发与探索能力。
“着力解决问题最突出、矛盾最集中、群众要求最紧迫的水利问题,增强民生水利保障能力,扩大民生水利成果,使水利更好地惠泽民生,造福人民群众。”水利部部长陈雷的话语掷地有声,在代表们心中产生强烈共鸣。
基于此,本文结合文献[12]提出的全局引导蜜源搜索策略来改进IWO算法,对算法的探索能力进行提高,从而对算法中早熟现象进行避免,进一步改善IWO算法的全局寻优能力,下面给出了结合蜂群搜索机制的IWO算法步骤:
1)设置主要初始参数;
2)随机产生P个初始杂草位置,进入循环;
3)杂草根据式(10)计算繁殖种子个数;
4)根据式(11)计算种子分布的标准差,并正态分布在杂草周围;
5)根据式(9)计算适应度值并存储最优解;
6)种子根据式(13)搜索邻近候选解;
7)计算新种子的适应度值,并选取更优的种子;
9)存储此时的最优解;
10)循环次数加1;
11)满足终止条件,达到最大循环次数。
2.3 改进DV-Hop算法的流程
本文借助于IWO算法较强的寻优能力,在将DVHop算法未知节点坐标计算问题成果转换为全局最优化求解问题的基础上,结合人工蜂群全局最优引导策略,在对IWO算法进行改进以提高其收敛速度和搜索精度后,提出了基于人工蜂群搜索机制的IWO算法的DV-Hop改进算法,记为BWDV-Hop算法。以期较好地解决求解未知节点坐标时误差较大的问题,图1给出了算法的流程。
3 实验结果及分析
为了验证改进算法的有效性,仿真平台均基于MATLAB实现,并对传统DV-Hop算法、文献[6]提出的ADVHop算法进行比较。设监测区域为边长等于100 m的方形区域;BIWO算法初始种群P为10,P_Max为30,迭代次数为30,σinitial=3,σfinal=0.000 1,smax=5,smin=0,搜索区间为[0,100];ABC算法初始种群SN=10,循环次数为30,limit=10。分别仿真比较了本文算法和文献[7]提出的ADV-Hop和标准DV-Hop算法中,在节点个数不同、锚节点个数不同及通信半径条件不同时的定位精度,通过仿真分析得出不同条件下算法的定位性能。本文通过计算归一化平均定位误差作为评价指标[12],试验结果基于500次独立仿真实验,计算公式为
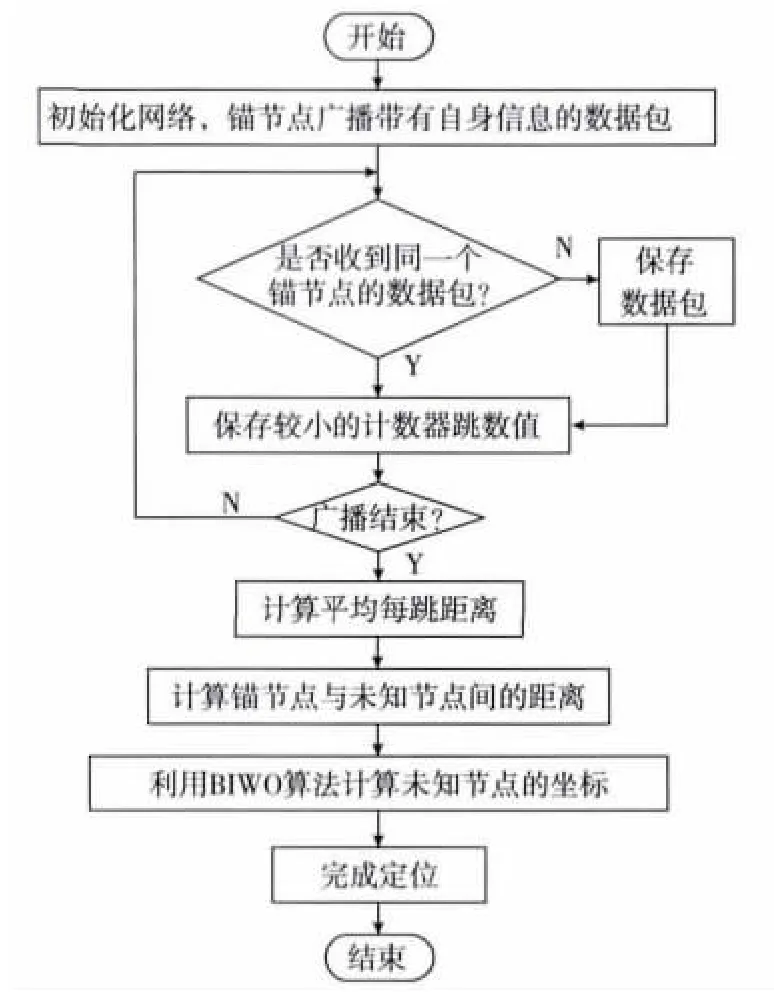
图1 BWDV-Hop算法流程

式中:m为锚节点个数;nc为可定位节点的个数;(xi,yi)为对未知节点的估计坐标,(x'i,y'i)为其实际坐标。
图2给出了3种DV-Hop算法归一化平均定位误差随传感器节点个数变化的曲线,其中锚节点比例为10%,节点通信半径R=22 m。由图2可以看出,在节点个数由60向240变化的过程中,3种算法的归一化平均定位误差均逐渐减小;另外BWDV-Hop的定位误差明显小于其他两种算法的定位误差,具体相比于DV-Hop和ADV-Hop算法分别减小了23.48%和13.53%。

图2 不同节点个数下的定位性能
图3给出了3种DV-Hop算法的定位性能随锚节点个数变化的曲线,其中节点通信半径R=22 m,节点总数为120。从图3中可以发现,当锚节点个数不断增多时,归一化定位误差对于三种算法来说均逐渐减小并趋于稳定,相比于DV-Hop和ADV-Hop算法,BWDV-Hop算法的平均定位误差分别减小了29.03%和19.43%。

图3 不同锚节点个数下的定位性能
图4为不同节点通信半径对3种DV-Hop算法定位性能的影响程度,其中节点总数为120,锚节点数为12。从图4中可以看出,随着节点通信半径的不断增加,3种算法的归一化平均定位误差均逐渐减小,相比于DV-Hop和ADV-Hop算法,本文提出的BWDV-Hop算法在归一化平均定位误差方面分别平均减小了14.57%和22.8%。

图4 不同通信半径下的定位性能
图5为传统DV-Hop算法、ADV-Hop算法以及本文提出的BWDV-Hop算法在边长为100 m的方形区域内的定位结果图。从图5可以看出,BWDV-Hop算法的定位误差小于DV-Hop算法以及ADV-Hop算法,且定位效果明显优于其他两种算法。
通过图5的仿真结果计算得出,当100个节点随机部署在边长为100 m的方形区域内,未知节点个数为90,锚节点个数为10,节点通信半径为20 m时,传统DV-Hop的平均定位误差为76.02%,ADV-Hop算法的平均定位误差为52.28%,而本文改进算法BWDV-Hop算法的平均定位误差为29.78%。
4 总结

图5 3种算法定位算法比较图
本文主要研究了无线传感器网络中,无需测距的DV-Hop定位算法。首先对DV-Hop算法的基本原理进行介绍,通过对算法原理的详细分析,总结算法产生误差的主要原因,在此基础上将未知节点位置的计算问题转化为全局最优化求解问题,通过设置目标函数,成功地将改进的入侵杂草优化算法引入到DV-Hop算法中。经仿真实验,验证了不同节点个数、锚节点个数及节点通信半径下,与标准DV-Hop算法和ADV-Hop算法进行比较,在定位精度与平均定位误差方面,本文改进算法具有明显优势。
:
[1]尚志军,曾鹏,于海斌.无线传感器网络节点定位问题[J].计算机科学,2004,31(10):35-38.
[2]LEE S,KIM K.Determination of communication range for range-free multi-hop localization in wireless sensor networks[C]//Proc.Computer Communications and Networks.[S.l]:IEEE Press,2011:1095-2055.
[3]PERKINS C,ROYER E.Ad hoc on demand distance vector routing[J].Mobile System and Applications,1999,24(3):59-81.
[4]NICULESCU D,NATH B.Ad hoc positioning system(APS)using AOA[C]//Proc.IEEE Computer and Communications Societies.San Francisco:IEEE Press,2003:1734-1743.
[5]ZHANG Dengyin,CUI Guodong.A union node localization algorithm based on RSSI and DV-Hop for WSNs[C]//Proc.Instrumentation,Measurement,Computer,Communication and Control(IMCCC).Harbin:[s.n.],2012:1094-1098.
[6]GUI L Q,WEI A,VAL T.A range-free localization protocol for wireless sensor networks[C]//Proc.International Symposium on Wireless Communication System(ISWCS).Paris:IEEE Press,2012:496-500.
[7]LI Mudong,XIONG Wei,LIANG Qing.An improved ABC-based node localization algorithm for wireless sensor networks[C]//Proc.International Conference on Wireless Communications,Networking and Mobile Computing(WICOM).Shanghai:IEEE Press,2012:1-4.
[8]WOO H,LEE S.Range-free localization with isotropic distance scaling in wireless sensor networks[C]//Proc.International Conference on Information Networking(ICOIN).Bangkok:IEEE Press,2013:632-636.
[9]MEHRABIAN A R,LUCAS C.A novel numerical optimization algorithm inspired from weed colonization[J].Ecological Informatics,2006(4):355-366.
[10]KARABOGA D,BASTURK B.On the performance of artificial bee colony(ABC)algorithm[J].Applied Soft Computing,2008,8(1):687-697.
[11]嵇玮玮,刘中.DV-Hop定位算法在随机传感器网络中的应用研究[J].电子与信息学报,2008,30(4):970-974.
[12]ZHU G P,KWONG S.Gbest-guided artificial bee colony algorithm for numerical function optimization[J].Applied Mathematics and Computation,2010,217(7):3166-3173.

