MIMO-OFDM系统ICI自消除改进算法
王振朝,张建平,种少飞
(河北大学电子信息工程学院,河北保定 071002)
MIMO-OFDM技术既有很高的数据传输速率,又可以克服无线信道频率选择性衰落[1],但是OFDM系统具有对频率和相位失真敏感的特点[2],尤其是易受载波频偏影响,使其子载波间的正交性遭到破坏,产生子载波间干扰ICI(Inter-Carrier Interference),而ICI使得系统的性能降低。所以如何消除ICI是MIMO-OFDM技术研究中的一大热点问题。
在抑制ICI的诸多方法中,ICI自消除算法由于其具有易于实现、抑制ICI效果好等特点而得到广泛应用。Zhao和Haggman首先提出了ICI自消除算法的基本原理及两根发射天线STFBC方案[3],之后Y.Gong和 K.B.Letaief在两根发射天线的基础上提出了多发射天线STFBC 方案[4],M.Uysal和 N.Al-Dhahir提出了将一组数据分别映射到相邻子载波和对称子载波——ICI自消除算法[4]。近年,研究者们又相继提出一系列的改进方案,包括分别在相邻子载波和对称子载波上传输数据取反信号、数据实数加权取反信号、数据共轭信号等算法[5-6]。
现有ICI自消除算法的研究,主要针对SISO-OFDM系统,对于MIMO-OFDM系统ICI自消除算法的研究还处于起步阶段。本文主要探讨MIMO-OFDM系统ICI自消除算法的基本原理,针对现有ICI自消除算法中实数加权取反算法在提高CIR时会降低系统的抗噪声性能这一问题给出改进方案:将一组复数加权共轭数据分别映射到相邻子载波和对称子载波上,这种算法能够改善系统因相位旋转而引进相位误差的问题,最后达到提高系统抗噪声性能的目的。
1 ICI自消除算法的基本原理分析
1.1 SISO-OFDM 系统 ICI分析
图1所示为频偏条件下的SISO-OFDM系统图。

图1 SISO-OFDM系统ICI分析
为了便于考虑ICI对系统造成的影响,将接收端和发送端的晶振频率不一致导致的频偏看作是在信道上乘以一个固定的衰减[7],在接收端暂时忽略噪声干扰,在接收端经过一系列的变化得到第k个子载波上的接收信号为
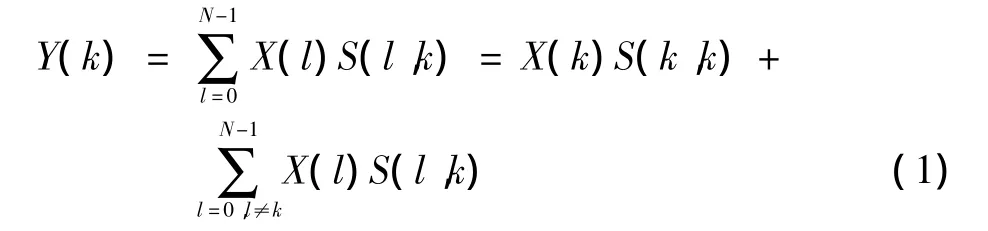
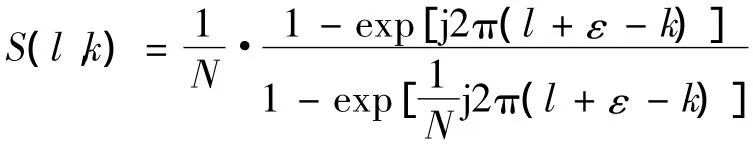
定义信号功率与干扰功率之比(Carrier to Interference Ratio,CIR)为系统ICI的量化评价参数。假设传输的信号在载波“0”上传输,忽略白噪声的影响,可以得出CIR的表达式为

SISO-OFDM系统的ICI自消除算法的基本思路是,将一组数据符号调制到一个子载波上,再将这组数据符号取反后调制到相邻的子载波上,在接收端将每个子载波中的信号按奇偶排序的规律进行合并来抵消ICI的影响。
令X(1)=-X(0),X(3)=-X(2),…,X(N-1)=-X(N-2),则解调出来的第2k个和第2k+1个子载波上的接收信号分别表示为

将式(3)与式(4)相减,使ICI相互抵消,得到的接收信号为

定义 ICI自消除的调制系数S'l-k=S2l-2k-S2l+1-2k,ICI自消除的解调系数S″l-k=2S2l-2k-S2l+1-2k-S2l-1-2k,ICI自消除调制和ICI自消除解调组合成ICI自消除算法,达到ICI自消除的效果。
载干比CIR可以表示为

1.2 MIMO-OFDM 系统 ICI分析
设MIMO-OFDM系统有M个发射天线和N个接收天线,OFDM调制的子载波数为K。系统结构如图2所示。

图2 MIMO-OFDM的系统模型
在接收端,接收天线n上的接收信号为

式中:zn(k)是均值为零的复高斯随机变量;Cm(k)为发送端STFBC映射的码字,可以表示为

Hm,n(k)为发射天线m和接收天线n之间信道的频域响应,可以表示为

式中:L为发送天线m和接收天线n之间的信道中的多径数;系数αm,n(t,l)表示的是发射天线m和接收天线n之间的第l路径的复增益,且满足均值为0、方差为,且;Δf=1/Ts,Ts为OFDM 符号周期;τl表示第l路径的延时。
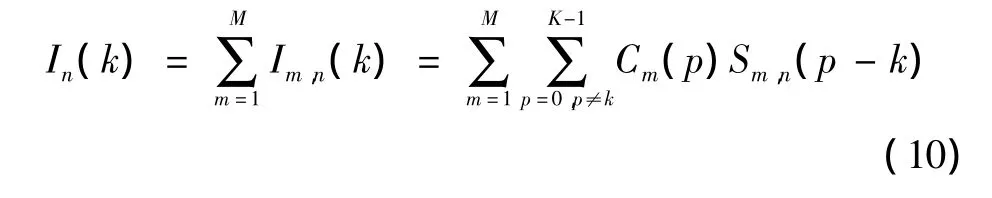


参考OFDM系统中的ICI自消除算法,MIMO-OFDM系统中也可以通过自消除算法来抑制ICI,但MIMOOFDM系统中的ICI自消除算法比较复杂。MIMO系统通过空时频编码,在发送端将要发送的信息映射到各天线上,在接收端进行解调,根据空时频编码准则,在接收端应用干扰消除调制方案。在接收端根据相应的规则进行解调,接收天线n上的第2k个和第2k+1个子载波上的接收信号分别为

将解调后的两个子载波式(12)和式(13)相减,可以得到抑制ICI的最后的解调信号为

载干比可以表示为
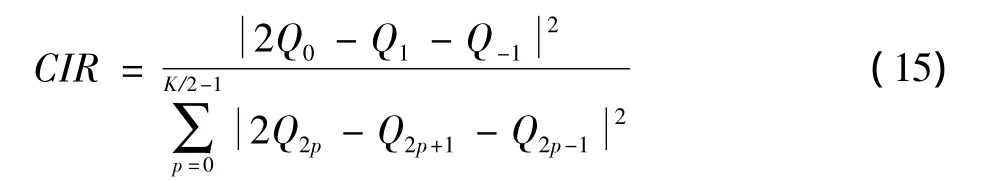
MIMO-OFDM系统中现有ICI自消除算法为分别在相邻子载波和对称的子载波上映射数据取反信号、数据实数加权取反信号、数据共轭的算法信号,这些算法中,数据实数加权取反算法的CIR最好,且它的CIR会随着加权因子减小而增大[9],但是加权因子过小会降低系统的抗噪声性能。这些算法并没有考虑因相位旋转而导致系统性能降低这一问题。
2 ICI自消除改进算法
针对实数加权取反算法中存在的问题,可以通过在发送端对数据进行复数加权运算来解决,是因为这种算法造成的相位旋转最小,可以有效地减少接收信号的相位误差,从而改善系统的抗噪声性能。
频偏引起的ICI系数会随着子载波位置的变化而变化[8],尤其是相邻子载波和对称子载波之间的ICI系数变化很小,所以本文将数据分别映射到相邻子载波和对称子载波上,从而最大程度地减小ICI系数。
文献[9]中提到了一种新的ICI自消除算法,在相邻子载波上发送共轭数据,最后仿真结果表明,这种方法可以提高系统的载干比且能够降低系统的BER[10-11],但这种算法同样存在因相位旋转而降低系统的抗噪声性能这一问题。综上,本文给出一种ICI自消除改进算法。
此时外面雨势稍减,方从云朝张位拱了拱手,闪身便出了轿子,张位连忙掀开窗帘去看,哪里还有方从云的影子?倒是一直在旁边躲雨的二管家吓了一跳,迎上前来:“老爷可有什么吩咐?这雨太大了,我让轿夫们先歇歇……”
2.1 相邻子载波上传输复数加权共轭数据
相邻子载波复数加权共轭数据传输算法的基本思想:将一组数据调制到子载波上,在相邻的子载波上发送复数加权共轭的数据。这种算法可以有效地减少接收机信号因相位旋转导致的相位误差,与现有ICI自消除算法作比较,这种算法可以降低系统由于相位误差带来的性能损 失。 映 射 方 法 为X(1)=ejπ/2X*(0),X(3)=ejπ/2X*(2),…,X(K-1)=ejπ/2X*(K-2),解调后天线n上的第2k个子载波和第2k+1个子载波上的接收信号分别可以表示为

类似一般的自消除算法对信号进行解调,将式(16)和式(17)加权相减,则解调信号为
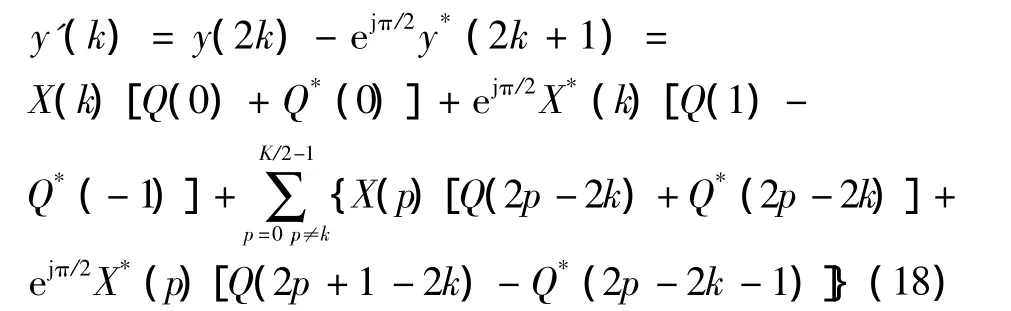
可以得到改进方法的载干比(CIR)为

2.2 对称子载波上传输复数加权共轭数据
在传输复数加权共轭数据的基础上提出一种改进方案,其主要思想是:改变在相邻的子载波上传输复数加权共轭数据,而在对称子载波上进行映射,即调制后第K-k-1个子载波上的数据是第k个子载波上的数据取共轭再将相位旋转π/2。
令X'(k)=X(k),X'(K-k-1)=ejπ/2X*(k),则天线n上的第k个子载波和第K-k-1个子载波上的接收信号分别为

根据相应的规则,将式(20)和式(21)加权相减,则解调信号为

则这种方法的载干比可以表示为
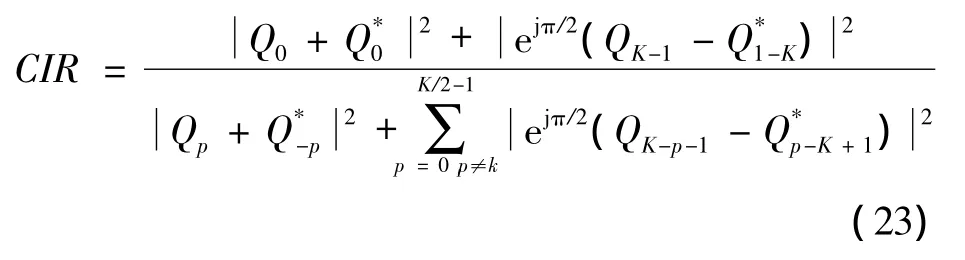
3 系统仿真与性能分析
为了验证本文算法的有效性,对系统进行MATLAB仿真比较。令子载波数为64,归一化频偏为0.3,对标准OFDM系统ICI干扰系数和ICI自消除调制系数和ICI自消除解调系数进行比较,仿真结果如图3所示。

图3 ICI干扰系数的比较
如图3所示,OFDM系统ICI干扰系数最大,ICI自消除调制的系数较小,ICI自消除解调的系数最小,说明ICI自消除算法可以抑制接收信号的ICI。
将标准OFDM系统、相邻子载波上数据取反算法、相邻子载波上实数加权取反算法、相邻子载波上和对称子载波上数据复数加权共轭算法的CIR进行仿真比较,结果如图4所示。

图4 几种算法的CIR比较
图4可以得到:整体比较这几种ICI自消除算法都能够提高系统的CIR,达到抑制ICI的作用;频偏较小时,相邻数据复数加权共轭算法的CIR最大;随着频偏的增大,相邻数据实数加权取反算法的CIR最好,且优于本文算法。
载干比是在忽略白噪声的情况下讨论的,为了分析这几种ICI自消除算法对系统性能的改善程度,可以通过对系统进行BER仿真。如图5所示是对标准OFDM、实数加权取反算法、相邻子载波上复数加权共轭算法和对称子载波上复数加权共轭算法的BER仿真。

图5 几种算法的BER比较
由图5可以看出,3种ICI自消除算法的BER都随着信噪比的增加而降低,这说明这3种算法都可以提高系统的抗噪声性能,与实数加权算法相比本文算法能够进一步降低系统的BER,说明本文算法可以更好地改善系统的抗噪声性能。
4 结论
小频偏条件下,ICI自消除算法能够很好地抑制MIMO-OFDM系统中的ICI,现有ICI自消除算法中实数加权取反算法抑制ICI的能力最好,但这种算法并没有考虑信号由于相位旋转造成的相位误差会降低系统性能这一影响,本文给出分别在相邻子载波和对称子载波上映射复数加权共轭数据的算法,这种算法可以有效地减小接收端信号的相位误差,从而能够提高系统的抗噪声性能。仿真结果表明本文算法与现有ICI自消除算法都能够抑制ICI,虽然本文算法在载干比的标准上抑制ICI的能力没有完全优于现有自消除算法,但本文算法降低了系统的BER,有更好的抗噪声性能。
:
[1]STAMOULIS A,DIGGAVI S N,AL-DHAHIR N.Intercarrier interference in MIMO - OFDM[J].IEEE Trans.Signal Processing,2002,50(10):2451-2464.
[2]金益峰.MIMO-OFDM系统中 ICI消除[D].上海:上海交通大学,2006.
[3]ZHAO Y,HAGGMAN S.Intercarrier interference self-cancellation scheme for OFDM mobile communication systems[J].IEEE Trans.Communication,2001,49(7):1185-1191.
[4]IDRIS A.CIR and BER Performance of STFBC in MIMO OFDM system[J].Australian Journal of Basic and Applied Sciences,2011,5(12):3179-3187.
[5]YIWLEAK A,PIRAK C.Zero-padded complex conjugate technique for intercarrier interference cancellation in MIMO-OFDM systems[C]//Proc.International Symposium on Communications and Information Technologies.Tokyo:IEEE Press,2010:901-906.
[6]IDRIS A,ALAM S,YUSOF S K S.A new data-conjugate intercarrier(ICI)self-cancellation for ICI reduction in space time frequency block codes MIMO-OFDM system[C]//Proc.2010 Second International Conference on Computer and Network Technology.Bangkok:IEEE Press,2010,43-47.
[7]康洁.MIMO-OFDM系统干扰消除技术的研究[D].西安:西安科技大学,2008.
[8]DAO D N,TELLAMBURA C.Intercarrier interference self-cancellation space-frequency codes for MIMO-OFDM[J].IEEE Trans.Vehicular Technology,2005,54(5):1729-1738.
[9]余华.高移动性环境下OFDM系统载波间干扰抑制技术[D].成都:西南交通大学,2010.
[10]周丽杰.OFDM无线通信系统中ICI自消除算法的研究[D].天津:南开大学,2009.
[11]IDRIS A,DIMYATI K.Interference self-cancellation schemes for space time frequency block codes MIMO-OFDM system[J].IJCSNS International Journal of Computer Science and Network Security,2008,8(9):139-148.
[12]MOLISCH A F,WIN M Z,WINTERS J H.Space-time-frequency(STF)coding for MIMO-OFDM systems[J].IEEE Communications Letters,2002,6(9):370-372.

