基于可变遗忘因子在OFDM系统的载波频偏估计

张军龙，刘立程，郝禄国

(广东工业大学信息工程学院，广东广州 510006)

OFDM技术作为第四代移动通信系统的核心技术［1］，其主要缺陷在于对CFO非常敏感，而CFO会破坏OFDM系统子载波间的正交性，引起子载波间干扰(ICI)。造成CFO的主要原因是由于发射机的载波频率和接收机本地振荡器频率之间的误差，或者是由于通信收发双方的相对移动而引发的多普勒频移。在高载频和高速移动环境中，由于多普勒扩展的增大使得无线信道往往表现为时间—频率双选择性衰落(时变)信道［2］，而时变信道极大地增加了信道的未知参量，通常需要通过建立基带扩展模型(BEM)［3］来简化信道的未知参量。

RLS自适应滤波［4］是通过对参数采用递推方式进行更新，以实现跟踪和适应系统或环境的变化，所使用的确定性线性回归模型是卡尔曼(KF)滤波算法［5］的一种特殊无激励的状态空间模型。将RLS自适应滤波应用到时变信道下OFDM系统CFO估计，提高了CFO估计的精度。与经典信号估计方法［6］(贝叶斯(Bayesian)估计法和最大似然(ML)估计法)相比，不仅避免了高阶矩阵求逆运算，可以减小计算量的同时也解决不可辨识问题［7］;而且避免了CFO估计的“搜索”过程，提高了运算效率。

在RLS算法中利用遗忘因子进行指数加权实现对各个时刻误差的遗忘作用，所以遗忘因子对RLS算法的收敛速度和跟踪能力有很大的影响，然而CFF－RLS算法无法同时满足对CFO估计的快速跟踪能力和足够小的估计误差的需求。为了解决传统的RLS算法［8］在收敛速度与收敛精度方面对遗忘因子要求的矛盾，本文提出了两种可变遗忘因子方案，来适应RLS算法对遗忘因子的要求。与CFF－RLS算法相比较，VFF－RLS算法既能确保对CFO具有快速跟踪能力，同时又能保证具有足够小的CFO估计误差。

1 系统模型

在OFDM系统的发送端，由导频符号和数据符号构成的帧结构如图1所示［8］，则一个OFDM符号的时域发送数据(或导频)为x(n)，其中n∈［－Ng，N－1］，N为子载波数，Ng为循环前缀(CP)的长度。

图1 发送符号的帧结构示意图

为了减少时变信道的未知参量，可以通过建立BEM模型［3］来表示时变信道。根据采用的基函数种类不同，主要的BEM模型有复指数BEM(CE－BEM)、多项式BEM(P－BEM)和卡洛 BEM(KL－BEM)。其中 CE－BEM 模型采用的基函数是傅里叶基，对应的信道第l个抽头的时域离散冲激响应为

在接收端，经过时变的多径信道后，假设系统在时间和相位上同步，考虑到CFO的影响，接收到的时域信号为

式中:ε为归一化频偏(小数倍频偏);L为信道的路径总数;w(n)为零均值的复高斯白噪声。

2 基于VFF－RLS的CFO估计

2.1 CFF－RLS 算法

根据时域的接收信号，建立关于CFO的最小二乘(LS)代价函数，其第i次迭代的RLS表达式［7］为

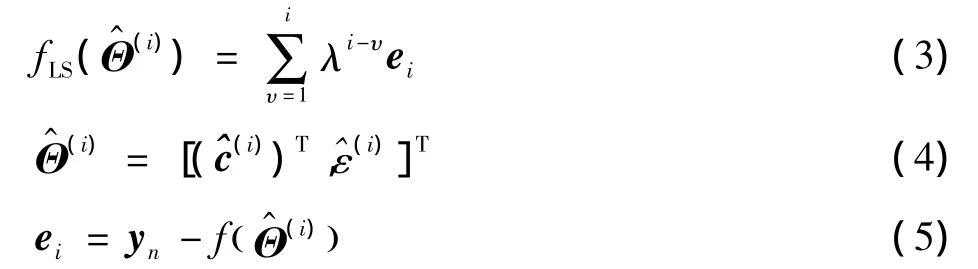
式中:加权因子λ为遗忘因子(Forget Factor，FF);ei为估计误差;yn为实际滤波输出信号;f)为期望的输出号;为信道和频偏的状态向量，CE－BEM系数

为了使得ei可以进行线性迭代运算，通过对式(5)利用一阶泰勒级数逼近，得到

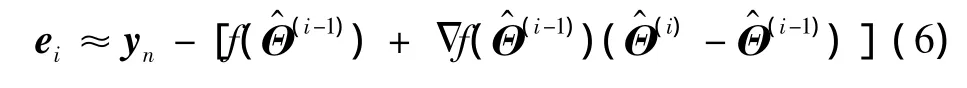
代表估计参量的梯度向量表示为

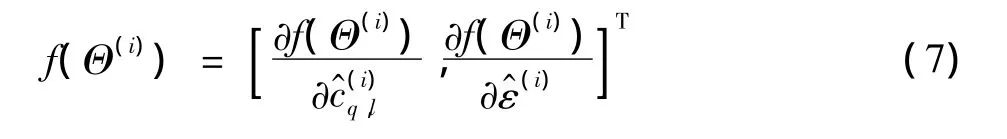
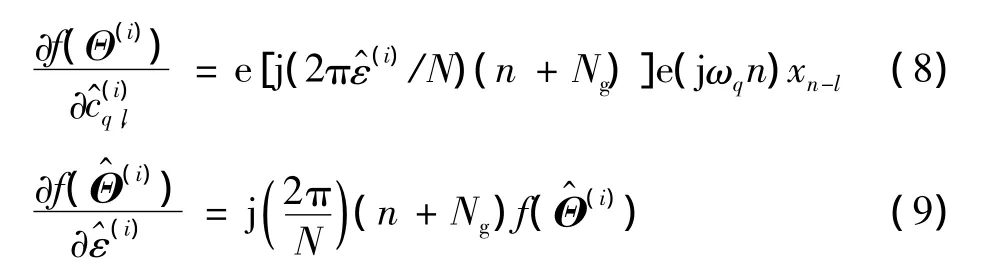
2.2 改进的VFF－RLS算法

式(3)中遗忘因子λ的作用是对离i时刻越近的误差加较大的权重，而对离i时刻越远的误差加较小的权重，即λ对各个时刻的误差具有一定的遗忘作用。遗忘因子的取值范围为0＜λ＜1，当λ=1相对于各时刻的误差无任何遗忘功能，此时RLS退化为一般的最小二乘方法(LS)。反之，λ=0表示只有现时刻的误差起作用，而过去时刻的误差完全被遗忘，不起任何作用，有文献进一步规定遗忘因子取值范围为0.9＜λ＜0.995［9］。

将式(3)展开得到

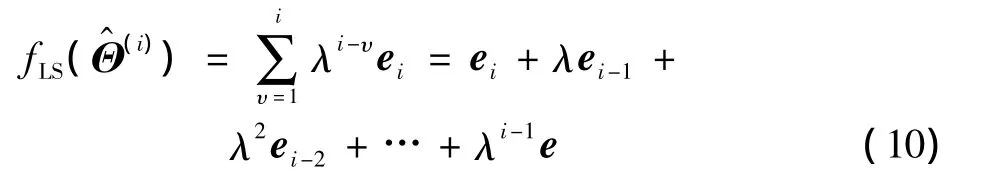
由式(10)可知，传统RLS算法取固定λ，若λ取值越小，代价函数就越接近最新的误差，对前面误差遗忘的越快，跟踪效果就越好，能够提高参数估计的收敛性，但是参数估计误差有所增加，同时会影响算法的稳定性。若λ取值偏大，可以保证足够低的估计误差，但是在初始阶段参数的估计性能不是非常的理想，收敛性较差，算法的跟踪效果较弱。所以，CFF－RLS算法不能同时满足收敛速度和参数估计误差，需要在跟踪速度与稳定性之间进行折中［8］。

因此，考虑采用VFF－RLS来提高CFO的估计性能。当初始阶段或者系统动态变化时，取较小的遗忘因子以跟踪动态参数的变化;当系统趋于平稳时，取遗忘因子趋于1，从而获得较小的稳态误差。基于这一准则，本文分别提出线性遗忘因子RLS(LFF－RLS)和非线性遗忘因子RLS(NLFF－RLS)估计法进行CFO估计，如图2所示。

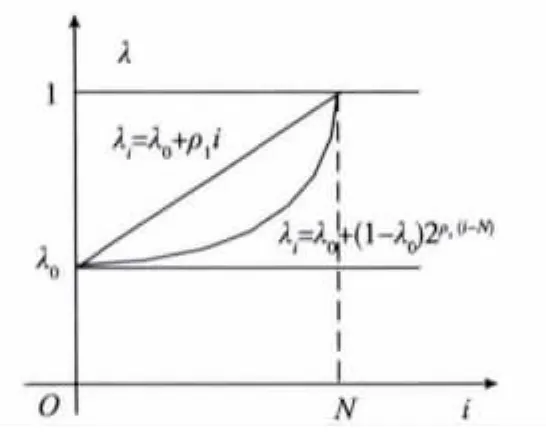
图2 可变遗忘因子的示意图

其中LFF表达式为

式中:λ0为起始值;ρ1为线性遗忘因子λi的步长参数。

NLFF表达式为

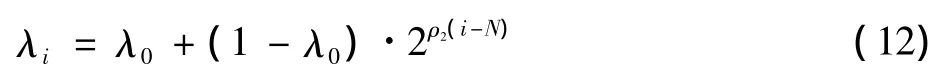
式中:λ0为起始值;ρ2为非线性遗忘因子λi的学习速率参数;N为迭代的次数。

根据标准RLS算法的CFO估计流程，则本文提出的LFF－RLS算法和NLFF－RLS算法具体步骤如下:

1)首先进行初始化，即

式中:Ρ1为初始化值;系数γ为正规化参数。经过以下的重复运算和参数更新完成RLS算法的递推，实现CFO的估计。

2)重复过程:第i次迭代过程更新参数表达式为

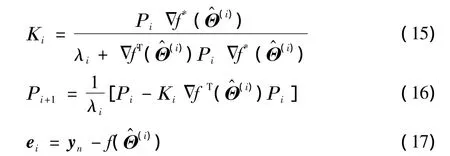
3)更新第i次迭代估计为

3 仿真分析

仿真参数如下:载波频率为fc=2 GHz，采样频率为fs=1.92 MHz，子载波数N=128，循环前缀Ng=10，一个帧结构包含15个OFDM子符号、3个导频符号。信道采用JAKE模型［3］，共5条路径，CE－BEM模型基函数Q=2，OCE －BEM 模型k=2，正规化参数 γ =0.01，遗忘因子的起始值 λ0=0.8，参数 ρ1=0.001 55，参数 ρ2=0.05。

通过选取不同的常量遗忘因子(即图3中的λ)，采用CE－BEM模型，对OFDM系统CFO估计性能进行比较。图3所示的是在信号接收端的移动速度5 km/h，归一化载波偏移量ε0=0.01下CFO估计的均方误差值，可以看出，当遗忘因子λ取较大值时，在高信噪比的情况下，可以保持足够低的均方误差，可是在低信噪比时，性能表现的较差;当遗忘因子λ取较小值时，虽然在低信噪比的情况下，可以降低CFO估计的均方误差，但是在高信噪比时，性能表现的有所降低。由此验证CFF－RLS无法同时满足CFO估计的收敛速度和足够小的均方误差，需要利用可变的遗忘因子来改善CFO的估计性能。

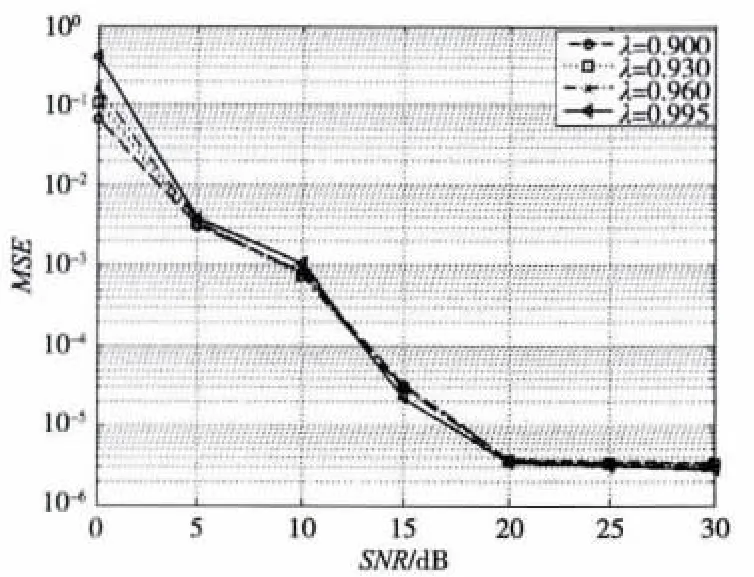
图3 CFO估计的均方误差 ，ε0=0.01，v=5 km/h

图4所示的是在信号接收端的移动速度10 km/h，归一化载波偏移量 ε0=0.01下，通过采用 CE－BEM和OCE－BEM两种时变信道模型，对3种遗忘因子设计方案的CFO估计性能进行比较。其中A1为λ取固定值0.95的CFF－RLS算法，A2为LFF－RLS算法，A3为 NLFF－RLS算法。相比较CFF－RLS算法、LFF－RLS算法和NLFFRLS算法表现的性能更优。由A2、A3可以看到，当在递推的过程中采用可变的遗忘因子λ，既能在低信噪比时降低均方误差，也能在高信噪比时呈现足够好的CFO估计性能。在不同的BEM模型下，LFF－RLS算法和NLFFRLS算法呈现的均方误差各有高低，关键在于可变遗忘因子是否适应系统的动态变化。

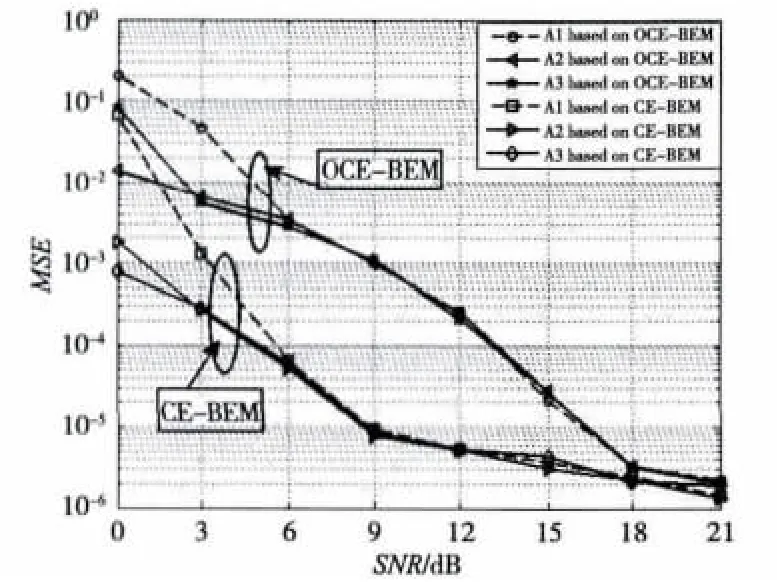
图4 CFO的估计的均方误差 ，ε0=0.01，v=10 km/h

图5所示的是在移动速度50 km/h，信噪比SNR=5 dB下，在不同CFO取值情形下CFO估计性能的比较。当采用OCE－BEM模型，在CFO取值小于0.2时，VFFRLS算法的CFO估计性能要明显优于CFF－RLS算法，而且CFO估计性能保持稳定;当采用CE－BEM模型，在CFO取值小于0.1时，VFF－RLS算法的CFO估计性能优于CFF－RLS算法，其中相比较NLFF－RLS算法的CFO估计性能，LFF－RLS算法表现的稍显“逊色”。随着CFO取值的增大，导致时变信道下OFDM系统CFO估计性能开始恶化，VFF－RLS算法对CFO估计性能的改善作用渐渐减弱，3种方案的CFO估计性能越来越接近。

4 结论

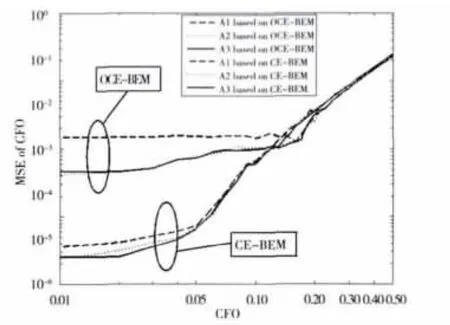
图5 CFO估计的均方误差，SNR=5 dB，v=50 km/h

本文提出了线性变化遗忘因子和非线性变化遗忘因子两种方案的改进RLS算法，用来改善时变信道下OFDM系统CFO估计性能。通过与CFF－RLS算法的CFO估计均方误差比较，可变的遗忘因子既可以对CFO保持快速跟踪能力，又可以确保足够小的CFO估计误差。因此，可变的遗忘因子更加适合在时变信道环境中对OFDM系统CFO的估计，需要注意的是控制好遗忘因子的变化速度以及初始值。

:

［1］汪裕民.OFDM关键技术与应用［M］.北京:机械工业出版社，2007.

［2］梁婷，王玲，戴香玉.OFDM系统中时变信道下信道估计方法的研究［J］.电视技术，2006，30(9):4－7.

［3］RABBI M F.High mobility orthogonal frequency division multiple access channel estimation using basis expansion model［J］.IET Communicaiton，2010，4(3):353－367.

［4］赵春晖，张朝柱，王立国，等.自适应信号处理技术［M］.北京:北京理工大学出版社，2009.

［5］SIMON E P，HIJAZI H，ROS L，et al.Joint estimation of carrier frequency offset and channel complex gains for OFDM systems in fast time－varying vehicular environments［C］//Proc.IEEE International Conference on Communications Workshops.［S.l.］:IEEE Press，2010:1－5.

［6］RICKLIN N，ZEIDLER J R.Data－aided joint estimation of carrier frequency offset and frequency－selective time－varying channel［C］//Proc.IEEE International Conference on Communications.［S.l.］:IEEE Press，2008:589－593.

［7］GAO F F，NALLANATHAN A.Identifiability of data－aided carrier－frequency offset estimation over frequency selective channels［J］.IEEE Trans.Signal Processing，2006，54(6):3653－3657.

［8］NGUYEN－LE H，THO L N.Pilot－aided joint CFO and doubly－selective channel estimation for OFDM transmissions［J］.IEEE Trans.Broadcasting，2010，56(4):514－522.

［9］HAYKIN S.Adaptive filter theory［M］.4th ed.Englewood Cliffs，NJ:Prentice－Hall，2002.