智能视频监控系统中运动目标跟踪的研究

许慧芳，许亚军

(太原理工大学信息工程学院，山西太原030024)

作为智能监控的基础组成部分之一，运动目标跟踪与目标检测一样是监控领域的重要问题和关键技术，也是计算机视觉与人工智能研究领域中具有相当挑战的热门研究课题之一［1］。智能视频监控中，运动目标跟踪是建立在目标有效检测的基础上、位于行为描述与理解之前的关键技术，它可以为数据融合、图像理解、场景描述等后续处理提供重要的操作平台。现阶段运动目标跟踪已经被广泛地应用在工业生产监督、医学研究、交通流量观测监控、自动导航、图像检索和恢复、天文观测等领域。

目标跟踪的技术思路是利用运动目标的位置、纹理、形状、颜色、轮廓等特征，采取某些具有特定目的的算法，通过帧图像之间对应匹配关系确定目标轨迹等相关信息，并对感兴趣目标的运动路径及状态进行确定，从而实现对视频序列中运动目标的实时跟踪［2］。图像序列目标匹配过程中，具有真正使用价值的跟踪算法需要满足三个标准，即能够在提高跟踪准确性和鲁棒性的同时保证系统运行的实时性。近年来人们从这三个评估因素出发，提出了大量的创新改进的跟踪算法。由于在不同的应用领域对运动目标跟踪的要求是不同的，目前为止并没有一种跟踪算法能够兼顾三者，因此有限的时间内目标跟踪技术还不能达到人类所需的各种场景，还有许多值得研究、改进和完善的问题。

1 基于均值偏移的跟踪算法研究

均值偏移(Mean－Shift)，顾名思义，首先计算规定的起始点的偏移均值量，该数量值就是起始点移动的距离值;将起始点移动之后的位置作为新起点，继续沿着密度函数的梯度方向移动，最后收敛于一个局部最优点。Mean－Shift是一个连续迭代的循环，实质就是通过迭代不断地寻找目标的新的位置点。实际应用中，Mean－Shift跟踪算法的目标模板经常使用图像的颜色特征来确定，下面就基于颜色特征的Mean－Shift算法在目标跟踪方面的应用进行具体阐述和推导。

设跟踪目标的中心在图像的原点处，并且用矩形表示跟踪目标，其空间坐标为x*i(i=1，2，…，n)，目标颜色空间被均匀地分散在m个直方图区间。令目标模型的直方图为 p=［p1，p2，…，pm］T，每个直方图区间的直方图计算如下

设候选区域目标的坐标为xi(i=1，2，…，n)，它的直方图表示为q(z)=［q1(z)，q2(z)，…，qm(z)］T，其中q(z)如下

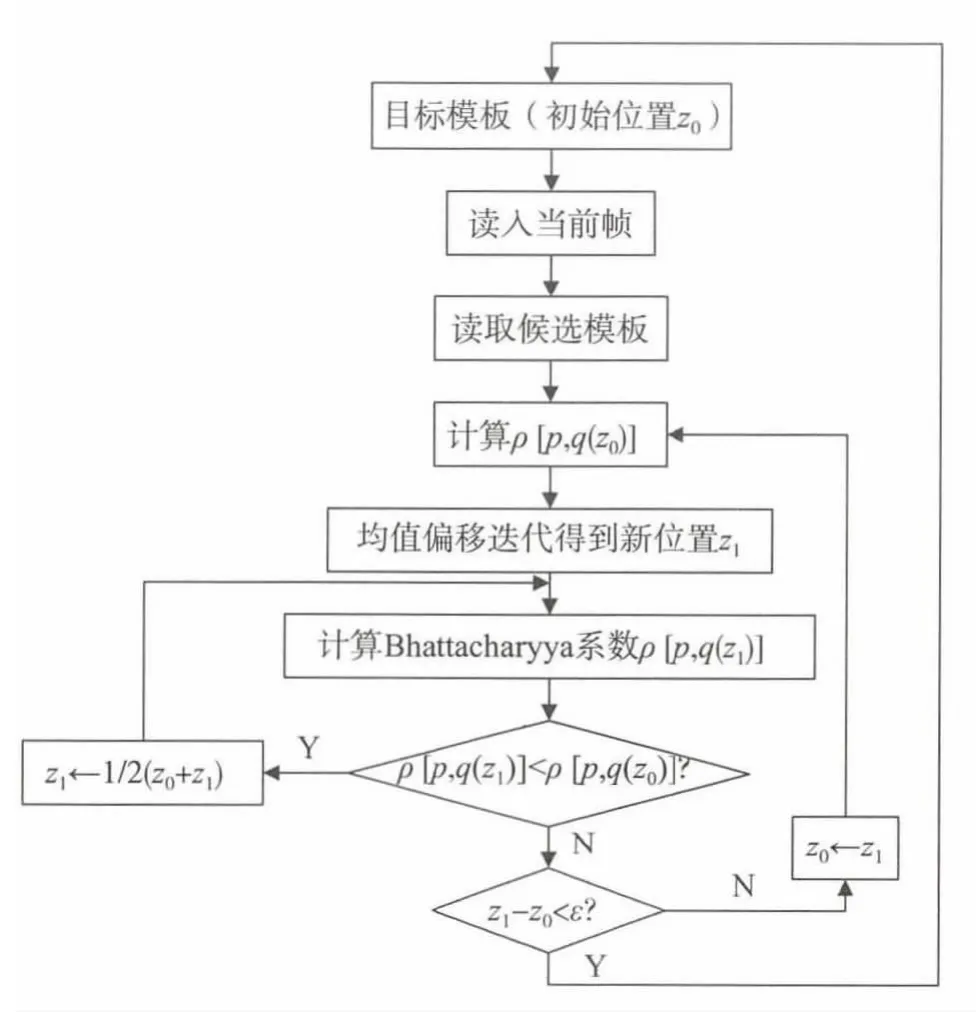
图1 Mean－Shift算法流程

目标模型与候选目标模型之间的巴氏距离如下

式中:ρ［p，q(z)］即为巴氏系数 Bhattacharyya［3］，形式如下

puqu(z)的极小化就是d(z)得极大化。跟踪目标的初始位置设定为z0，通过推导可以得出

如前所述，Mean－Shift算法是建立在均值偏移矢量连续自动迭代的基础之上。由算法流程图1可以看出Mean－Shift算法进行跟踪主要分为3个步骤:1)初始化搜索窗即设定跟踪目标窗口，也就是目标模板的大小;2)分别计算目标模板的中心、质心位置，利用均值偏移向量将模板的中心移动到质心位置;3)重复步骤2)中目标模板中心到质心的移动，直至找到Bhattacharyya系数取极大值的位置，即目标的真实位置。

2 基于粒子滤波的跟踪算法研究

粒子滤波器是基于贝叶斯估计、蒙特卡洛模拟提出的一种实时推理算法。简单来说，粒子滤波方法是用一组带权的样本粒子来表达一个后验概率分布。样本点在任意状态空间进行漂移、扩散、测量等循环过程，最后这些样本的权重乘以测量概率密度完成重采样过程，生成新的样本粒子，并根据给定的当前测量估计其似然度。粒子滤波具有灵活、易实现、并行化等特点，它可以很好地解决非线性、非高斯动态系统问题。下面从贝叶斯估计和蒙特卡洛采样两个方面对粒子滤波的原理进行阐述。

2.1 贝叶斯估计

系统模型和测量模型，这两者是利用贝叶斯估计理论进行动态系统分析必不可少的［4］。其中，系统模型用来表征随着时间的推移而变形演化的系统状态，也称为状态模型;描述与状态有关的带有噪声的测量模型也即观测模型。下面先引入两个状态方程

式中:ft表示状态转换函数;ht表示系统观测函数;系统在t时刻的状态由Xt来表征，t时刻对未知系统状态的观测由Zt来表征;vt表示系统状态误差，nt表示观测误差，可模型化为2组独立同分布不相关的噪声序列。

贝叶斯估计的根本在于，利用系统模型预测状态的已知信息得到系统状态变量的置信程度，也就是后验概率密度。用Bayes估计理解、认知并研究目标跟踪，就是在系统测量数据Z1:t已知的情况下，估算系统在t时刻的状态向量Xt的后验概率密度函数p(Xt|Z1:t)。如果，假定初始状态向量X0的先验概率密度函数为p(X0|Z0)，那么通过预测和更新的连续递归就应该可以得到系统状态向量的后验概率密度函数p(Xt|Z1:t)。

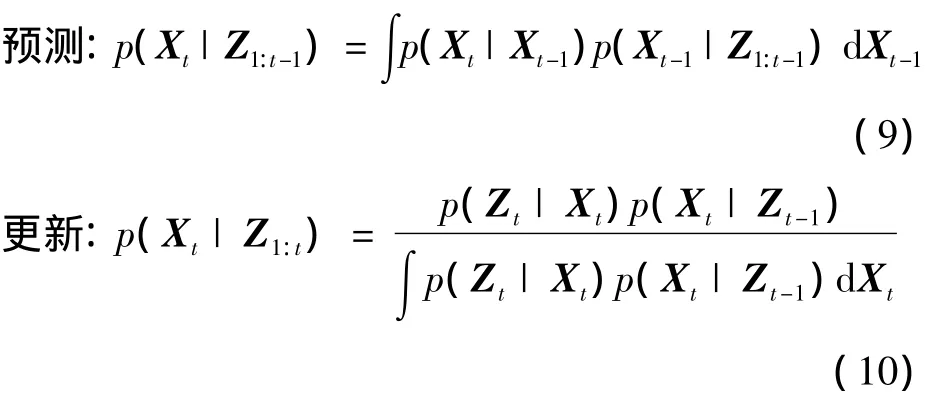
式中:p(Xt|Xt－1，Z1:t－1)=p(Xt|Xt－1)是一阶马尔科夫过程。状态变化的概率模型p(Xt|Xt－1)由状态方程决定。p(Zt|Xt)是表示t时刻的系统状态似然函数。由式(9)和式(10)共同构成了一个由先验概率密度p(Xt－1|Z1:t－1)到后验概率密度p(Xt|Z1:t)的递推过程。

2.2 蒙特卡洛采样

贝叶斯滤波器的递推，本文采用非参数化的蒙特卡洛粒子来模拟实现。蒙特卡洛又称作随机模拟方法，它利用随机抽样的方式来求解问题，其采样的实质是:采取一组随机样本，并给这些样本赋予权值，然后利用这些样本、样本权值以及对样本的估算，来求得后验概率分布，也就是状态的估计值。当样本数足够大的时候，蒙特卡洛特性就几乎等价于后验概率密度，那么蒙特卡洛粒子滤波器就无限接近于贝叶斯最优估计。图2为蒙特卡洛采样下的粒子滤波工作原理示意图。

图2 Particle Filter工作原理示意图

用集合 S= {，i=1，2，…，N}表示t－1时刻的N个样本，以及各样本被赋予的权值，∑=1。获得系统状态在k时刻的后验概率的步骤为:1)对N个样本进行重采样;2)利用状态方程对粒子进行预测;3)利用观测方程更新粒子权值=p(Xi k|Zk)。可以通过离散加权的办法求得t时刻的后验概率密度

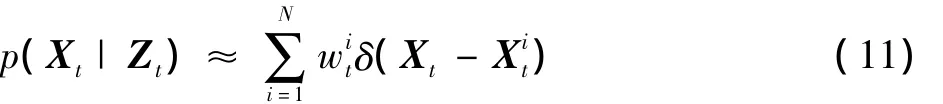
由于粒子滤波器的蒙特卡洛性质，粒子数目的多少决定着跟踪的精确度，粒子数目越多，粒子滤波对后验概率密度的估计越准确，跟踪的鲁棒性也就越强。相反的是，粒子数目越多，使计算量变大，实时性也变得更差。在实际应用中，通常需要平衡算法的准确性与实时性。

3 融合Mean－Shift的粒子滤波跟踪算法

归纳起来，Mean－Shift算法计算效率较高，算法复杂度低，实时性也较好，对目标变形有一定适应性，其跟踪的鲁棒性在很大程度上依赖于图像分析结果的可靠程度。但同时，Mean－Shift算法是一种局部优化方法，有时候不可避免地收敛于局部极值点。在目标跟踪方面，也就意味着其对目标被局部遮挡、完全遮挡的情形等不适应，并要求目标单帧移动距离不能太大。其次，Mean－Shift算法在目标颜色与背景颜色相近等低背景对比度的情况下，很容易造成目标的丢失，其抗干扰能力和鲁棒性都有待增强。

相反，由于粒子滤波器可以很好地解决非高斯非线性系统问题，其在很多方面的表现都比Mean－Shift算法强。最具有对比价值的就是，粒子滤波方法维持了目标的多种假设状态，具有非常强的处理目标遮挡问题的潜力，而且对低背景对比度下的目标跟踪也优于Mean－Shift算法。但是，由于粒子滤波的蒙特卡洛特性，在进行目标跟踪时需要大量的样本粒子，粒子数目的增加固然可以提高算法的可靠性，可是也使得算法复杂度和计算量急剧上升，进而导致实时性变差，这就需要对算法可靠性与实时性进行平衡折中。其次，滤波中的粒子面临不断退化的情况，尽管重采样算法可以降低退化的影响，但它同时也带来其他一些问题:粒子都必须被重新计算，重采样削弱了粒子的多样性。

基于这些分析，本文认为将Mean－Shift与粒子滤波相结合可以实现优势互补:粒子滤波可使Mean－Shift避免收敛到局部峰值点，增强抗遮挡性能;Mean－Shift算法的聚类作用可以对粒子重新配置，有效改善粒子退化现象，保证了粒子多样性，提高了采样效率，进而有效提高算法的可靠性、鲁棒性，使得粒子滤波算法可以用到对实时性要求高的场合。

本节提出的算法是建立在前两节算法理论的基础之上，因此算法基本原理不再叙述。重点分析如何将Mean－Shift与粒子滤波完美结合达到优化跟踪的目的。

首先引入一个概念:聚类分析。聚类分析的核心思想［5］就是依据同类样本之间的相似性，将一些未标签的样本集分成几个群类，各个样本群具有各自的相似性。换言之，聚类分析的作用就是汇集同一群类中的样本数据在一起，同时隔离不同群类中的样本数据。目前，聚类分析已经在智能控制、故障诊断等很多需要进行大量数据分析的领域产生了巨大影响。多数情况下，聚类分析的使用结合了密度估计方法。均值漂移的聚类作用即属于此类型。

接下来，要对目标模型更新进行探讨。本文采用的是基于颜色直方图分布的粒子滤波器，它的跟踪质量极易受到天气阴晴、光照条件以及可视角度等因素的影响。为了有效抑制干扰降低外界影响，目标更新环节的加入就显得尤为重要，其作用当然也非同寻常:在目标更新条件驱使下算法自行判断是否进行目标更新，从而保证当监控场景中存在太多噪声或发生遮挡时目标模型不被更新，而当目标重新出现时系统能迅速找到目标。这也就是粒子滤波具有处理目标被全遮挡和强抗噪性的原因所在。在此，给出目标更新条件的判决公式

式中:πT是判决门限，大量试验之后本文取值 0．8;πE［S］为E［S］的观测概率，E［S］表征样本集 S={，，i=1，2，…，N}的平均状态。

以k时刻的模板定义给出模型更新公式

经过如图2的重采样之后，采用加权的方式确定目标位置

融合Mean－Shift的粒子滤波算法，就是粒子在经过重采样和动态模型随机传播之后，加入能够对粒子进行聚集作用的均值漂移算法，使归属于不同群类的四面八方样本粒子向目标的最大化区域边缘定向移动。所以，可以更新粒子权重的时候最大可能地为每个样子粒子赋予较大的权重，从而实现使用较少样本粒子描述较多目标状态的功能。这样处理的结果就是，远离目标区域的粒子能够尽量地靠近目标，样本粒子“猜测”的成分降低，算法需要的总迭代次数减少，进而算法计算量大幅下降。图3为融合Mean－Shift的粒子滤波算法流程图。

4 实验结果分析

图3 融合Mean－Shift的粒子滤波算法流程

本文选用PETS2001/DATASET2中的视频测试序列［6］“CAMERA1”(大小 360 ×240，共 2 825 帧)来验证算法的有效性。图4为3种算法跟踪同一个蓝色小车的效果图，抽取其中的5帧图像进行分析，3种算法抽取的视频帧号由上至下依次为第 956，979，1 000，1 008，1 026帧，由左至右分别为均值偏移算法、粒子滤波算法、融合Mean－Shift的粒子滤波算法的跟踪结果。程序运行环境为 MATLAB 7．10，处理器为 Intel Core i5，主机CPU 2．50 GHz，内存 2 Gbyte。

由第956帧在3种算法下的跟踪结果图可以看出，图像都是目标在正常行驶情况下的跟踪结果，Mean－Shift算法跟踪目标边框相对较大，而另外两种没有明显差别，总体来说3种算法的跟踪效果都比较满意。第979帧的跟踪图像表示算法在目标被部分遮挡下的表现。由图可以看出，虽然近端的大树晃动对目标跟踪产生了一定的影响，但算法的跟踪效果没有受到明显干扰，只有Mean－Shift算法跟踪目标边框依旧相对较大，也反映了Mean－Shift算法跟踪精度相对较弱的实质。第1 000帧图像显示了3种算法在目标被完全遮挡情况下跟踪的差异，Mean－Shift算法已经完全丢失了目标，而后两者却仍然在继续移动。这就体现了之前分析的Mean－Shift算法对目标完全被遮挡的不适应性，而融合了Mean－Shift的粒子滤波算法由于其蒙特卡洛特性，目标跟踪仍然可以维持。当跟踪序列进行到第1 008和1 026帧的时候，Mean－Shift算法已经停滞不前，后两者能够迅速搜索到目标并继续完成目标的跟踪，并且跟踪非常准确。这更加充分地说明加入目标模板更新算法对重新搜索、定位并迅速跟踪目标的重要性。

图4 3种算法的跟踪结果对比

由图4还可以看出，粒子滤波、融合Mean－Shift的粒子滤波两种算法在跟踪效果方面几乎没太大差别，这是一种错觉，因为它们执行跟踪过程所用时间有极大的差距。3种算法所用平均执行时间以及样本粒子数如表1所示。

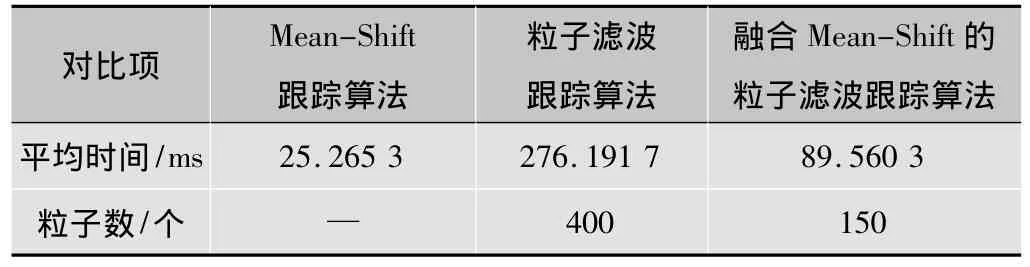
表1 3种算法平均执行时间以及所需粒子数

经过多次的跟踪试验，得知粒子滤波算法至少需要390个粒子才能获得相对准确的跟踪表现。为了保证跟踪可靠性，实验中选取了400个粒子。而融合Mean－Shift的粒子滤波算法最少只需要150个粒子。通过仿真，获知均值漂移跟踪算法执行时间平均为25．265 3 ms，执行时间最少;粒子滤波跟踪算法的平均执行时间为276．191 7 ms;而改进后的算法平均执行时间仅需要为89．560 3 ms。第三种算法在150个粒子条件下的跟踪效果几乎等同于粒子滤波选用400个粒子的跟踪效果。正是由于均值漂移对粒子的重新配置，很好地抑制了粒子退化现象，提高了采样效率，在降低计算量的同时提高了算法的精确度和实时性。

5 总结

本文对智能视频监控的关键技术——运动目标跟踪进行了研究，提出了一种融合Mean－Shift的粒子滤波目标跟踪算法，该算法提高了Mean－Shift算法在目标遮挡情况时的工作性能;同时，利用Mean－Shift对粒子样本的重新配置，降低了计算量，提高了采样效率，很好地抑制了粒子的退化现象，使得目标跟踪可靠性增强，提高了运动目标跟踪算法的实时性和鲁棒性。最后在MATLAB上进行了实验仿真，与传统的粒子滤波相比较，本方法具有算法复杂度低、鲁棒性较好、抗遮挡干扰强等特点，是一种有效的运动目标跟踪方法，可广泛应用于实时性要求较高的智能视频监控技术中。

:

［1］乌恩．智能视频监控中运动目标检测与跟踪算法研究［D］．长沙:国防科技大学，2010．

［2］ WANG H，WANG J T，REN M W，et al．A new robust objects tracking algorithm by fusing multi－features［J］．Journal of Image and Graphics，2009，14(3):489－498．

［3］ KUSHWAHA A K S，SRIVASTAVA R．Performance evaluation of various moving object segmentation techniques for intelligent video surveillance system［C］//Proc．2014 International Conference on Signal Processing and Integrated Networks(SPIN)．［S．l．］:IEEE Press，2014:196－201．

［4］袁国武．智能视频监控中的运动目标检测和跟踪算法研究［D］．昆明:云南大学，2012．

［5］ TISSAINAYAGAM P，SUTER D．Object tracking in image sequences using point features［J］．Pattern Recognition，2005，38(1):105－113．

［6］ PETS2001，The second IEEE international workshop on performance evaluation of tracking and surveillance［EB/OL］．［2014－07－20］．http://www．cvg．cs．rdg．ac．uk/PETS2001．