基于最优小波基的主泵裂纹转子特征识别研究
李 彬,夏 虹
(哈尔滨工程大学 核科学与技术学院,哈尔滨 150001)
反应堆主冷却剂泵作为核电厂的一个重要组成部分,其运行状态直接关系核电厂的运行安全,从第一座核电站运行至今,由于主冷却剂泵的故障引起的核电厂停堆事故达到多起,造成了重大经济损失。而作为主冷却剂泵的一个主要核心部件——转子的特性直接决定了主泵的运行状态,所以对转子故障特征的监测与识别能够及时有效地保证反应堆的安全运行以及减少不必要的维护费用。
小波分析方法由于其良好的分析特性己经在旋转机械的故障诊断中得到了广泛应用,但是其在工程应用中仍然有一个重要的难题没有解决——小波基的选择问题。不同的小波基具有不同的性质,对信号的分析能力也不同,对同一信号采用不同的小波基得到的结果也不同[1-3],在小波应用中,多数采用离散的 db小波或者haar小波,也有少部分利用连续的morlet小波[4]。众多学者也积极对这一领域开展研究,例如,Yang等[5]利用最大形状匹配的原则来确定适合振动信号的小波基,Schukin等[4]利用最小总误差和时频分辨率的规则来选择适合冲击信号的小波基,但是多数研究结果也都只是从某一方面来确定适合特定信号的小波基。
小波变换后的小波系数表明了小波与被处理信号之间的相似程度,如果小波系数较大,则表明小波和信号的波形相似程度较大;反之则比较小。所以,本文提出基于小波系数与信号之间的互相关系数的方法来选取合适的小波基。通过对反应堆主冷却剂泵裂纹故障进行建模仿真,获取故障信号,然后利用选取的小波基信号进行故障特征识别。
1 最大互相关系数法
将任意L2(R)空间中的函数f(t)在小波基下展开,称这种展开为函数f(t)的连续小波变换(CWT),其表达式为[6]:
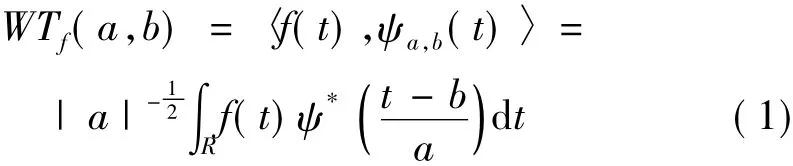
我们称WTf(a,b)为小波系数,它反映信号与小波基的相似程度为连续小波基函数,通过调整尺度参数a和平移参数b,可以得到具有不同时-频宽度的小波以匹配被测信号的任意位置,达到对信号的时-频局部化分析的目的。
小波变换实质上就是分析信号与小波基在不同尺度上的相似性,根据这个特点,我们引入了互相关系数——用来描述两个变量相互之间密切程度的数字特征量。由于小波系数能够描述被测信号的局部特征,所以其就成为了联系小波基与信号的纽带,而小波系数与信号之间的互相关系数自然也就能够刻画小波基与被测信号的相似程度,即当互相关系数绝对值越接近1时,表示小波基与被测信号越相似。
结合互相关系数的定义,我们重新给出小波系数与被测信号之间互相关系数的公式:
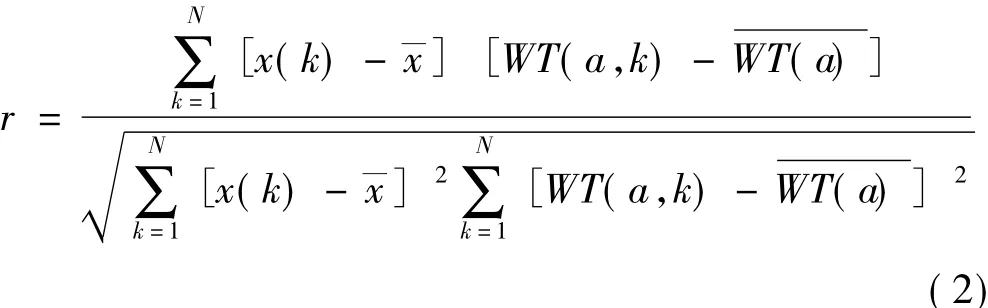
其中,N是被测信号x(n)的序列长度,WT(a,k)是被测信号x(n)在尺度a上的第k个小波系数,WT(a)和—x分别表示为尺度a上的小波系数和被测信号的平均值。利用这个公式,我们能够计算出在尺度a上小波系数与被测信号的互相关系数,然后,再通过比较不同的小波基与被测信号的互相关系数,确定使互相关系数最大的小波基作为最优小波基,我们称这种方法为最大互相关系数法。本文中主要从以下18种小波基中选择被测信号的最优小波基,它们分别为:haar、meyr、morl、mexh、db2、db4、db6、db8、db10、db12、db16、sym2、sym4、sym6、sym8、coif1、coif2、coif3 等,它们的特点如下表1中所示:

表1 不同小波基函数的特点Tab.1 Characteristics of different wavelet basis functions

图1 裂纹模型Fig.1 Model of crack
2 反应堆主冷却剂泵裂纹转子振动模型
目前,大多数裂纹转子系统模型的研究是基于水平转子[7-8],而反应堆主冷却剂泵一般情况下是垂直安装,所以要充分考虑轴承和基础对转子的影响,基于此,本研究结合有关裂纹转子的刚度模型[9](图1)建立了垂直安装主泵的裂纹转子-轴承-基础的振动模型,如图2所示,其中m1为泵体等效质量;O1为m1的质心;c1为泵体支撑阻尼;k1为泵体支撑刚度;m3为轴等效质量;O3为m3的质心;m2为等效圆盘质量;Oe为等效圆盘质心;y表示径向;O2为轴心;c2为转子阻尼;2kp为转轴刚度。该模型的振动微分方程如公式5所示,式中:x、y为各个等效质量的径向振幅;c、k分别为阻尼和刚度;e为等效圆盘的偏心距;m为各个等效质量;w为轴转速;t为时间;φ为初始相位角。
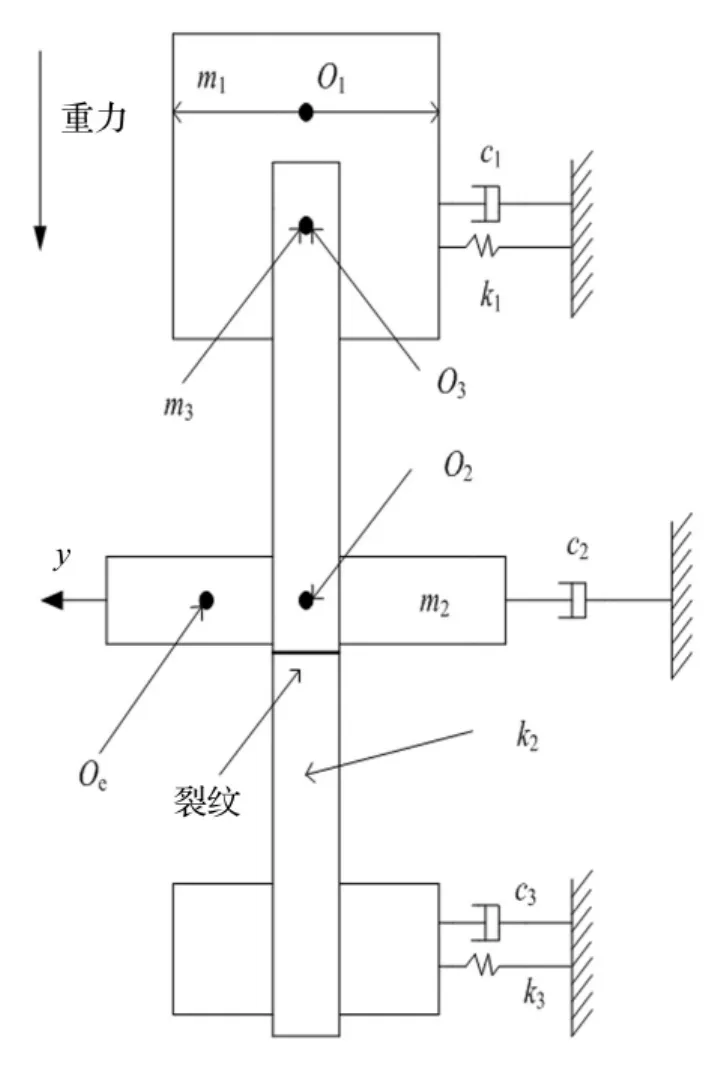
图2 反应堆主冷却剂泵裂纹转子模型Fig.2 Model of the cracked rotor of RCP

在上面的微分方程中,裂纹转子的刚度表示为如下式子:
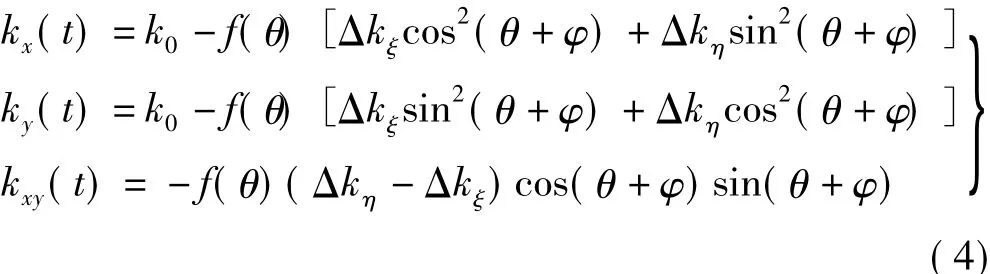
其中,f(θ)为开关函数,其表达式如下[8]:

在公式(4)和(5)中,θ=wt+φ+β-,其中 可由tan=得到,β为转子偏心方向与裂纹方向的夹角,α可以通过cosα=求出,R、T分别为轴直径和裂纹深度,k0为无裂纹时的初始刚度,Δkη、Δkξ为有裂纹时的刚度变量。R-T
3 主泵转子裂纹故障特征识别
由于主泵垂直安装,重力在径向几乎不起作用,在动挠度远大于静挠度的前提下,可采用开裂纹形式[10],即开关函数f(θ)=1。而由于转子裂纹的出现,使转轴的刚度不对称,从而引发非线性振动,出现旋转频率的1倍、2倍、3倍等高倍分量。
现设转轴转速w=2 200 r/min,m1=200 kg,m2=220 kg,m3=30 kg,c1=4 300 N·s/m,c2=9 300 N·s/m,c3=3 000 N·s/m,k1=5.26×107N/m,k2=2.104 ×108N/m,k3=5 ×107N/m,e=0.2 mm,φ =0,α=,β=0,这里裂纹取在 ξ方向上,kη=2.004×108N/m,kξ=1.8×108N/m。其仿真信号及其傅里叶变换如图3和图4所示,其中采样频率为2 000 Hz。从原始信号的傅里叶变换图中,可以清晰地看出转子的旋转频率,其值为36.7 Hz,并不能识别出裂纹转子的高倍分量故障特征。
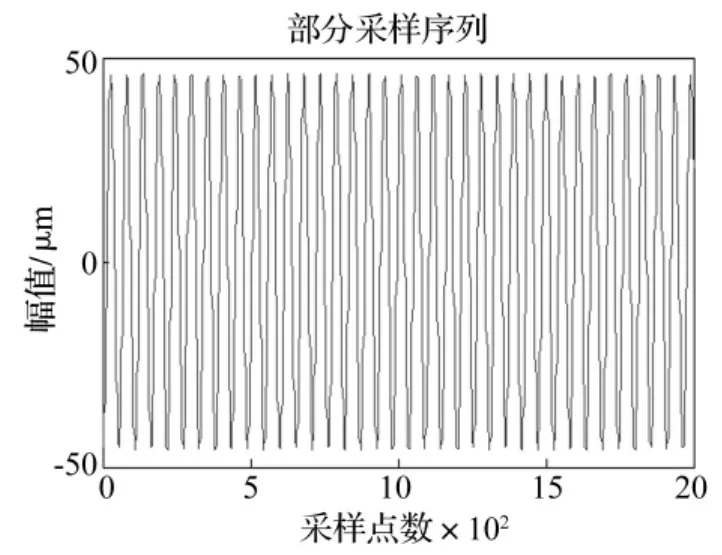
图3 转速2 000 r/min开裂纹信号Fig.3 The open crack signal at the speed of 2 000 r/min
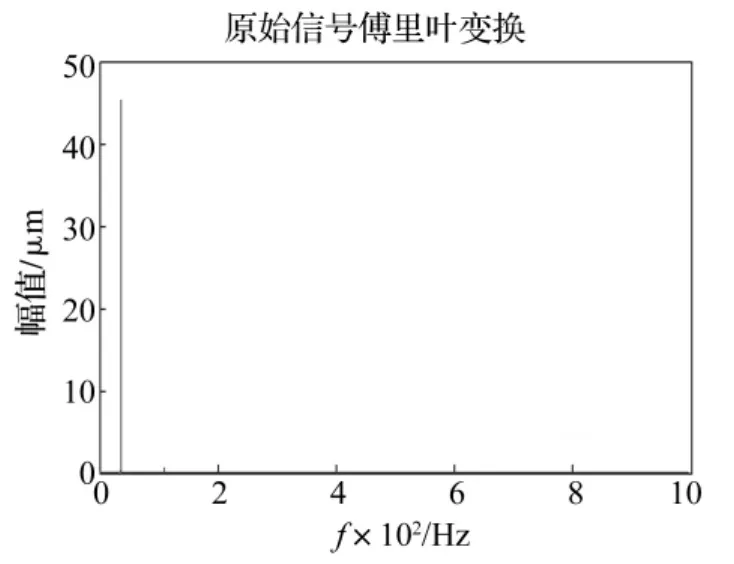
图4 信号傅里叶变换Fig.4 FFT of the signal
下面,我们采用最大互相关系数法来选取原始信号的最优小波基。首先,我们利用上面的18种小波基分别与信号计算互相关系数,如图5所示。我们取其中互相关系数最大的db8小波、互相关系数较小的meyer小波以及互相关系数与db8较为接近的db12小波这3种代表性的小波分别对信号进行连续小波变换,并将小波变换结果以功率谱的形式刻画出来,如图6、图7和图8,对比分析结果确定最优小波基以及开裂纹信号的故障特征。
从db8小波的分析图中可以清晰地分辨出除了作为旋转频率的1倍频外,还存在3倍频与5倍频(5倍频的能量相对较小),因此db8小波能够识别出裂纹转子的高倍频分量,除此之外,随着尺度的变化,功率谱的光滑性也说明了db8小波在不同尺度上的识别能力都比较好。meyer小波对信号的分析结果如图7所示,虽然识别出了3倍频,但是其没能识别出5倍频,并且,该小波在不同尺度上对故障特征的识别能力也相差较大。而互相关系数与db8相差不大的db12小波,如图8所显示的,能够识别出3倍频和5倍频,但是其在低尺度上的识别能力较差。所以,作为互相关系数最大的db8小波,不仅有效识别出了裂纹转子的故障特征,而且在不同尺度上都能够很好地实现对故障特征的识别,因此,db8小波可以作为该仿真信号的最优小波基,并且从功率谱上也能够确定3倍频是其主要故障特征。
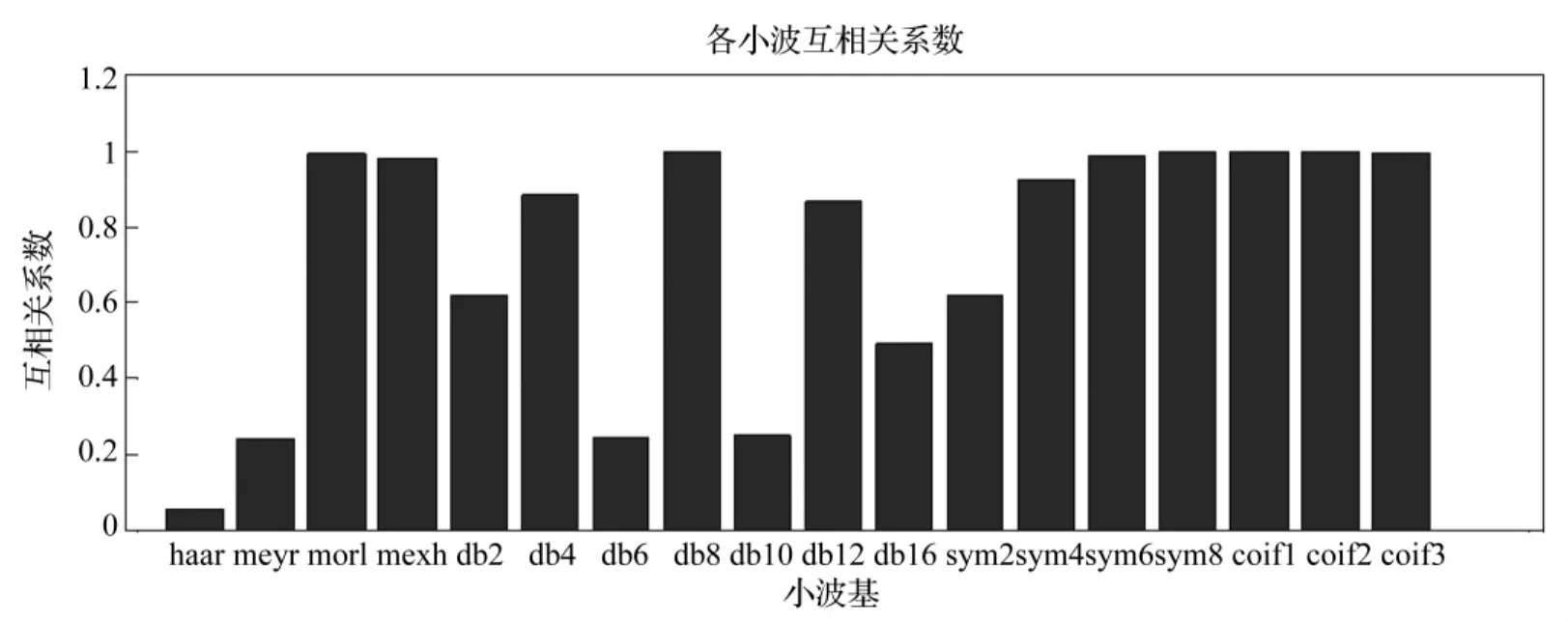
图5 信号与不同小波基的互相关系数Fig.5 Cross-correlation coefficients between the signal and various wavelet basis
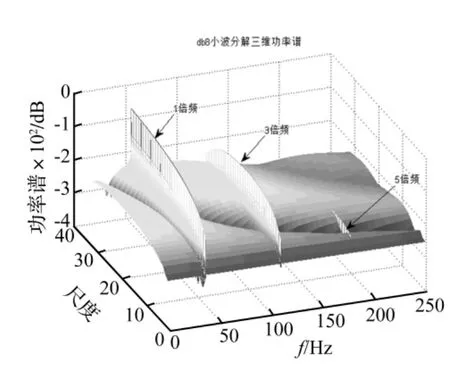
图6 db8连续小波变换功率谱Fig.6 Power spectrum of db8 CWT
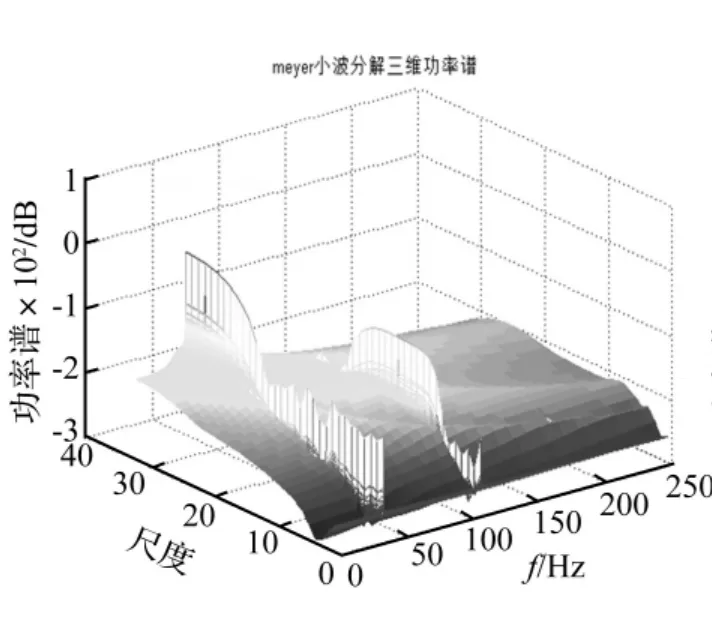
图7 meyer连续小波变换功率谱Fig.7 Power spectrum of meyer CWT
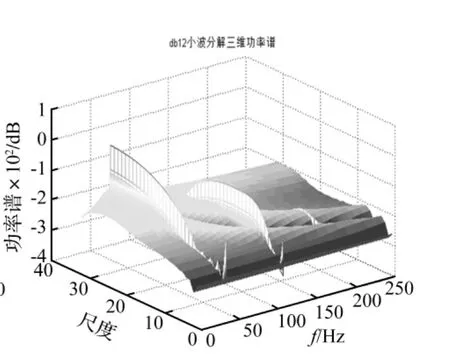
图8 db12连续小波变换功率谱Fig.8 Power spectrum of db12 CWT
为了更好地验证最大互相关系数法能够选取分析信号的最优小波基,我们不妨取另一组开裂纹振动信号进行分析,现设转子的转速为1 100 r/min,所得到的仿真信号以及傅里叶变换结果如图9、10。
从信号的傅里叶变换结果中,我们能够观测到,信号的旋转频率为18.3 HZ,并且除了旋转频率外,还存在一个3倍频。接下来,我们采用最大互相关系数法计算信号与不同小波基的互相关系数,如图11所示,系数最大的为mexh小波。我们仍然选取与mexh小波较为接近的coif1小波以及互相关系数最小的db10对信号进行分析对比,结果如图12、13和14所示,mexh小波不仅能够识别信号的旋转频率和3倍频,而且识别出了5倍频以及7倍频(能量较小),并且在各个尺度上,都有较好的识别能力。coif1小波虽然也能够识别出信号的3倍频、5倍频以及7倍频,但是随着尺度的增加,其识别能力变差,而db10小波的分析结果明显较差。
因此,作为互相关系数最大的mexh小波,不仅能够识别裂纹信号的3倍频、5倍频等故障特征,而且其在不同尺度上都具有较好的识别能力,所以,mexh小波可以作为该仿真信号的最优小波基,此外,从小波分析结果中,我们也能够得出3倍频是该振动信号的主要故障特征。
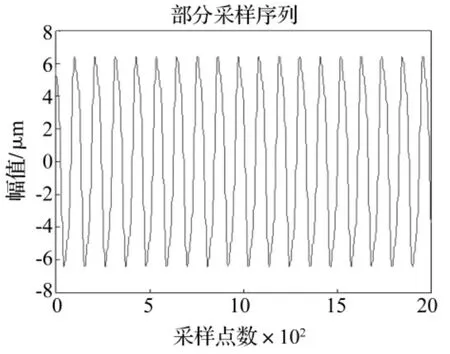
图9 转速1 100 r/min开裂纹信号Fig.9 The open crack signal at the speed of 1 100 r/min
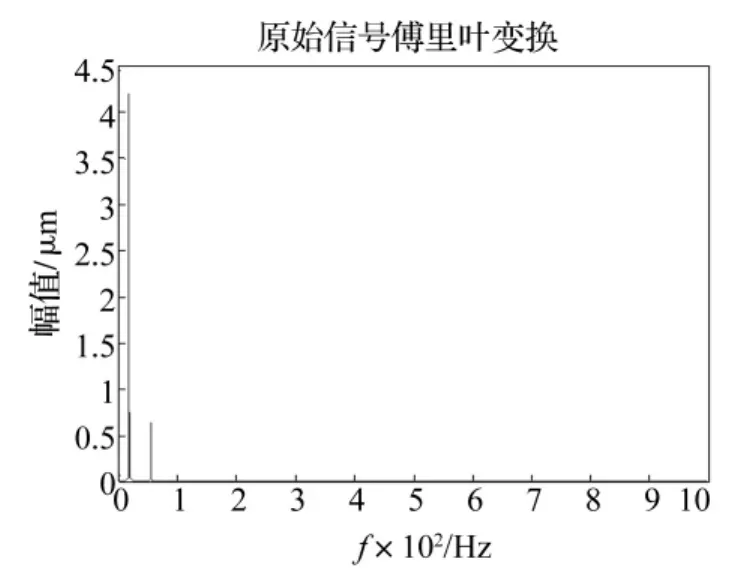
图10 信号傅里叶变换Fig.10 FFT of the signal

图11 信号与不同小波基的互相关系数Fig.11 Cross-correlation coefficients between the signal and various wavelet basis
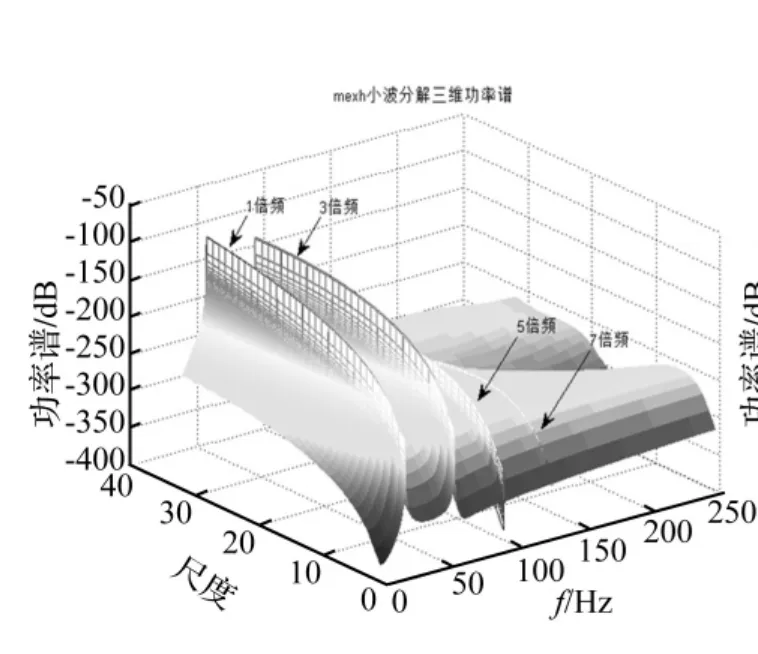
图12 mexh连续小波变换功率谱Fig.12 Power spectrum of mexh CWT
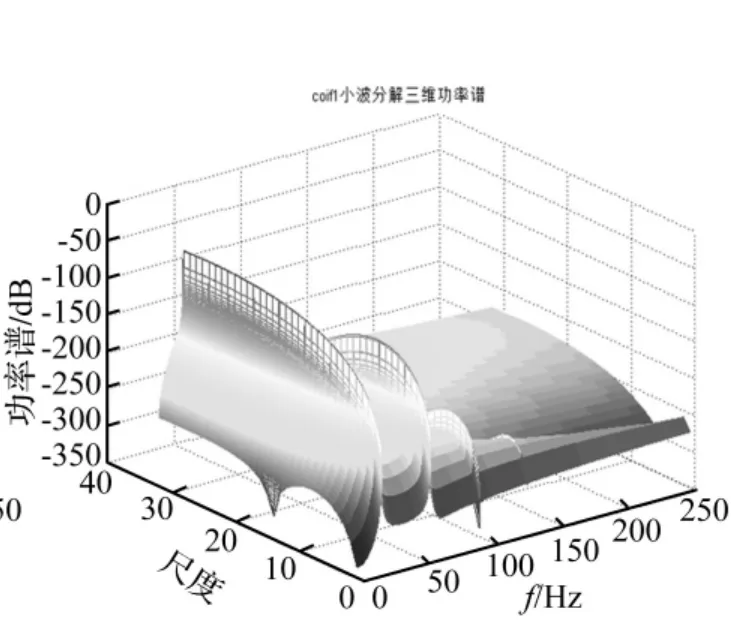
图13 coif1连续小波变换功率谱Fig.13 Power spectrum of coif1 CWT
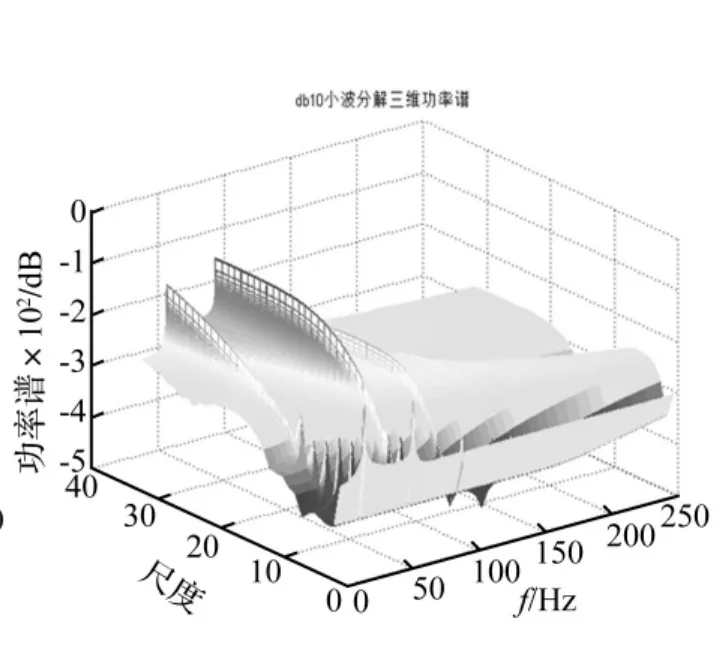
图14 db10连续小波变换功率谱Fig.14 Power spectrum of db10 CWT
4 结论
本文基于主冷却剂泵的裂纹转子的振动仿真模型,通过从小波基库中选取18种不同的小波基,分别计算这些小波基与两组不同转速的开裂纹故障信号之间的互相关系数,并选取3种具有代表性的小波基分别对故障信号进行小波变换,从分析结果中可以得出:
(1)最大互相关系数法能够实现两组不同转速的开裂纹故障信号的最优小波基,分别为db8与mexh小波;
(2)在该仿真模型下,虽然转速不同,但是转子开裂纹信号的主要故障特征频率都是3倍频。
由于本文只是从18种不同的小波基中选取信号的最优小波基,所以在小波基的选择范围上还有待扩展。此外,只考虑了开裂纹故障信号,并没有将噪声的影响考虑在内,所以今后还需要进行更加深入的探讨研究。
[1]郑钧,侯锐锋.小波去噪中小波基的选择[J].沈阳大学学报,2009,21(2):108-110.ZHENG Jun,HOU Rui-feng.Selection of wavelet base in denoising of wavelet transform[J].Journal of Shenyang University,2009,21(2):108 -110.
[2]孔国杰,张培林,徐龙堂,等.信号奇异性检测中的小波基选择及其工程应用[J].机械科学与技术,2009,28(4):542-545.KONG Guo-jie,ZHANG Pei-lin,XU Long-tang,et al.Selection of wavelet base in signal singularity detection and its application[J].Mechanical Science and Technology for Aerospace Engineering,2009,28(4):542 -545.
[3]田幕玲,王晓玲.电机故障诊断中的小波分析方法及小波基选取[J].煤矿机械,2007,28(5):176-178.TIAN Mu-ling,WANG Xiao-ling.Wavelet analysis method applied in fault diagnosis of motor and selection of wavelet base[J].Coal Mine Machinery,2007,28(5):176 - 178.
[4] Schukin E L,Zamaraev R U,Schukin L I,The optimization of wavelet transform for the impulsive analysis in vibration signals[J].Mechanical Systems and Signal Processing,2004,18(6):1315 -1333.
[5]Yang W X,Ren X M,Detecting impulses in mechanical signals by wavelets[J].EURASIP Journal on Applied Signal Processing,2004,8:1156 -1162.
[6]杨建国.小波分析及其工程应用[M].北京:机械工业出版社,2005.6.
[7]闻邦椿,顾家柳,夏松波,等.高等转子动力学[M].北京:机械工业出版社,1998.
[8]杨丹,甘春标,杨世锡,等.含横向裂纹Jeffcott转子刚度及动力学特性研究[J].振动与冲击,2012,31(15):121-126.YANG Dan,GAN Chun-biao,YANG Shi-xi,etl.Stiffness and dynamical behavior of Jeffcott rotor with cross crack[J].Journal of Vibration and Shock,2012,31(15):121 -126.
[9]高建民,朱晓梅.转轴上裂纹开闭模型的研究[J].应用力学学报,1992,9(1):108 -112.GAO Jian-min,ZHU Xiao-mei.Study on the Model of the shaft crack opening and closing[J].Chinese Journal of Applied Mechanics,1992,9(1):108 -112.
[10]夏虹,黄华,陈志辉,等.基于频率补偿小波的屏蔽主泵裂纹转子识别[J].原子能科学技术,2010,44(7):841-847.XIA Hong,HUANG Hua,CHEN Zhi-hui.Identification of cracked rotor of canned motor pump based on wavelet analysis of frequency compensation[J].Atomic Energy Science and Technology,2010,44(7):841 -847.

