正交变传动比面齿轮的设计及三维造型*

林 超，李莎莎，龚 海

(重庆大学 机械传动国家重点实验室，重庆 400044)

面齿轮传动是一种圆锥齿轮与圆柱齿轮相互啮合的齿轮传动[1]，圆锥齿轮(面齿轮)采用直齿渐开线齿轮刀具经范成加工而成.常见的面齿轮按传动位置关系可分为正交、非正交、偏置正交和偏置非正交4种情形[2-5].按照齿形分为直齿面齿轮、斜齿面齿轮和弧齿面齿轮[6-11].目前，相交轴间的变传动比传动主要是利用非圆锥齿轮副来实现的[12]，然而非圆锥齿轮副的设计与加工相当困难，正交变传动比面齿轮副是在深入研究非圆锥齿轮副的基础上设计的，由一个非圆柱齿轮和特殊非圆锥齿轮(变传动比面齿轮)组成.与非圆锥齿轮副相比，正交变传动比面齿轮副的最大特点是设计与加工更简单，可以利用现有的机床和刀具对其进行加工，易实现批量生产.正交变传动比面齿轮在纺织机械、农用机械、工程机械、汽车等场合有着广阔的应用前景，所以对正交变传动比面齿轮的研究有很重要的理论意义和工程应用价值[13].

正交变传动比面齿轮目前还无法通过三维软件对其进行直接造型，而齿轮的三维模型是进行有限元分析、机构仿真、数控加工等不可缺少的，为此，从正交变传动比面齿轮设计基本原理和插齿加工原理出发，利用VB和Solidworks的二次开发工具，开发一套该面齿轮参数化设计及仿真加工系统，实现快速设计，大大减少重复设计量，缩短设计周期、提高设计效率.正交变传动比面齿轮仿真加工系统可在计算机上模拟加工过程，得到该面齿轮三维模型并真实、直观地展现其展成原理、复杂加工过程和效果，为进一步的分析及制造研究奠定基础.

1 几何设计

1.1 节曲线设计

本文讨论的非圆柱齿轮节曲线为椭圆曲线(包括低阶椭圆和高阶椭圆)，其节曲线方程为[14]：

(1)

式中:a为椭圆的长轴半径；k1为椭圆的偏心率，n1为椭圆的阶数.

建立正交变传动比面齿轮副的坐标系如图1所示：坐标系s1(x1,y1,z1)和s2(x2,y2,z2)为动坐标系分别与非圆柱齿轮和正交变传动比面齿轮刚性固接.坐标系s10(x10,y10,z10)和s20(x20,y20,z20)为定坐标系，与切齿机床的机座刚性固接.初始时，坐标系s1和s10，s2和s20重合.R为正交变传动比面齿轮节曲线所在圆柱齿轮的半径，θ1，θ2分别为非圆齿轮、正交变传动比面齿轮转角.

图1 正交变传动比面齿轮副设计坐标系

根据空间啮合原理及空间坐标变换关系得到由s1(x1,y1,z1)转换到s2(x2,y2,z2)转换矩阵为：

(2)

根据齿轮啮合原理的推导，正交变传动比面齿轮的节曲线在坐标系s2(x2,y2,z2)用下列矩阵方程表示：

(3)

定义n2为正交变传动比面齿轮的阶数，表示该面齿轮节曲线在0～2π范围内变化的周期个数.根据节曲线封闭的条件有：

(4)

式中：i12为正交变传动比面齿轮副传动比.

根据式(1)(4)算得R,带入式(2)得到正交变传动比面齿轮节曲线参数方程为：

(5)

由式(3)可以看出，正交变传动比面齿轮节曲线的x，y坐标表示的是一个半径为定值R的圆，而z坐标则是随着θ1变化的，所以正交变传动比面齿轮的节曲线是圆柱面上的空间曲线.

1.2 齿顶齿根曲线设计

正交变传动比面齿轮的齿顶高和齿根高沿其节曲线法线方向计算，其齿顶曲线与齿根曲线是节曲线的等距曲线，它们与节曲线之间的法向距离分别是齿顶高ha和齿根高hf.由于直接基于圆柱面求齿顶曲线和齿根曲线的表达式比较困难，将正交变传动比面齿轮节曲线展开为平面曲线，推导出其齿顶、齿根曲线方程.参照非圆齿轮的齿顶齿根计算方法，得到正交变传动比面齿轮的齿顶曲线直角坐标表达式：

(6)

齿根曲线直角坐标表达式：

(7)

式中：

1.3 齿面方程

如图2所示，刀具渐开线齿面方程为：

(8)

式中：τ=θos+θs，rbs为刀具基圆半径，θs为刀具渐开线上一点的角度参数，μs为刀具渐开线上一点的轴向(沿zs方向)参数，θos确定刀具在基圆上的齿槽宽，并且对标准渐开线刀具用式(9)方程表示：

(9)

式中：Zs为刀具齿数；α0为压力角.

根据空间坐标变换关系得刀具坐标系osxsyszs到正交变传动比面齿轮动坐标系s2(x2,y2,z2)的转换矩阵[15]为：

(10)

式中：γ=ψ+θ1；

A=Dsinβ2sinθ2-Rcosθ2；

B=-Dsinβ2cosθ2-Rsinθ2；

C=r(π)-Dcosβ2．

ψ由公式(17)给出，D,β2在图4中标出．

图2 刀具渐开线齿廓

正交变传动比面齿轮齿面Σ2是由刀具齿面Σs包络而成，Σ2可表示为：

(11)

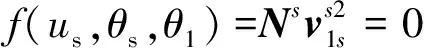
1.4 齿宽设计

1.4.1 正交变传动比面齿轮不根切的最小内半径

正交变传动比面齿轮与一般的定传动比面齿轮传动一样，也存在根切现象.由于根切的存在，正交变传动比面齿轮的齿宽会受到限制，因此对其根切现象的研究是十分必要的，根据齿轮传动无根切的通用条件[16]，可以得到加工刀具根切界限线的方程组：

(12)

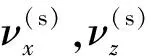
(13)

式中：ras为刀具齿顶圆半径.

(14)

1.4.2 正交变传动比面齿轮不变尖的最大外半径

正交变传动比面齿轮齿顶变尖的几何特征是轮齿两侧齿面相交其齿顶厚等于零.图3是正交变传动比面齿轮y2o2z2平面的轴截面示意图，R1和R2分别表示其最小内半径和最大外半径.因为y2o2z2平面是正交变传动比面齿轮轮齿两侧齿廓的对称平面，所以正交变传动比面齿轮齿顶变尖处应在y2o2z2平面上，参考图3，则变尖出的坐标为：

x2=0,y2=-R2,z2=-rsm．

(15)

正交变传动比面齿轮的齿面方程是关于θs和θ1两个未知数的方程.由其齿面方程(11)和式(15)的第一和第三式可解出θs和θ1，从而得到正交变传动比面齿轮不变尖的最大外半径R2.

求得了正交变传动比面齿轮不根切的最小内半径和不变尖的最大外半径，正交变传动比面齿轮的齿宽可表示为：

B=R2-R1．

(16)

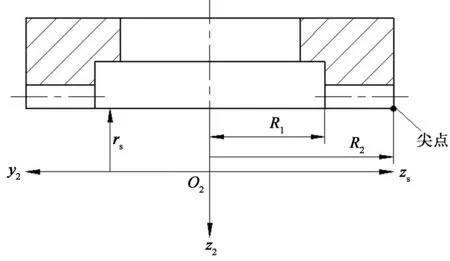
图3 最大外半径

2 三维造型

正交变传动比面齿轮齿面是很复杂的曲面，参考一般定传动比面齿轮的建模方法，基于现有的三维软件，主要的建模方法有NURBS自由曲面重构和虚拟加工方法.前者是根据面齿轮齿面方程运用数值方法求解齿面离散点，再在三维软件中进行曲面重构，实现面齿轮的几何建模.后者是基于布尔运算原理，模拟刀具和面齿轮毛坯的范成运动，在三维软件中直接实现面齿轮的几何建模.由于正交变传动比面齿轮数值求解过程抽象而繁琐，因此，本文选用虚拟加工方法在Solidworks软件中实现正交变传动比面齿轮的三维造型.

2.1 虚拟加工原理

正交变传动比面齿轮齿面是通过渐开线齿轮刀具与该面齿轮毛坯做范成运动形成的，运动过程中假想刀具与非圆齿轮内啮合.由于在Solidworks中无法实现实体的连续运动并且进行相关布尔运算，因此，可以靠每次微小角度的转动来模拟刀具和正交变传动比面齿轮毛坯的范成运动.切削该面齿轮的过程，实际上就是正交变传动比面齿轮毛坯与刀具作布尔减运算的过程.根据相对运动原理，可以假设其毛坯固定，刀具的节曲线在毛坯节曲线上作纯滚动，只要确定每一瞬时刀具的空间运动关系，再完成布尔减运算就能得到正交变传动比面齿轮的三维模型.由于在布尔减运算结果仅余被减物体，因此每次布尔减运算后，都应该对刀具进行复制，实际上每次正交变传动比面齿轮毛坯与刀具的布尔减运算，减去的是刀具的副本，刀具本身没有变化.仿真模型的精度是由每次刀具齿轮转动的步进角控制的，步进角越小，精度越高.

根据啮合原理和空间几何关系，加工刀具空间运动关系如图4所示.φ1，φ2分别为非圆齿轮、正交变传动比面齿轮转角，r3为刀具节圆半径.

图4 刀具空间运动关系示意图

刀具绕自身轴线旋转角度：

(17)

由微分几何可得：

(18)

由刀具发生纯滚动的弧长与非圆齿轮φ1角对应的弧长相等可得：

(19)

根据余弦定理：

(20)

(21)

x=Dcos (φ1-β2)．

(22)

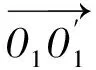
y=Dsin (φ1-β2)．

(23)

由传动比关系得，刀具绕面齿轮轴线旋转角：

(24)

正交变传动比面齿轮参数化仿真加工模块的程序流程图如图5所示．

2.2 软件设计

根据以上设计过程及仿真加工原理，基于visual basic语言与Solidworks开发平台，并结合matlab数学计算软件，设计出正交变传动比面齿轮参数化设计及仿真加工软件，其界面如图6所示．

参数化设计计算完成后，在仿真加工模块输入加工精度，加工起始角度和加工终止角度，依次点击生成刀具、生成毛坯、仿真加工按钮，程序会自动调用Solidwork软件，开始虚拟加工.

2.3 仿真加工实例

分别取n1= [2，3]，n2=[8,12]，k=0.1，z1=[26，27]，m=3，由正交变传动比面齿轮仿真加工程序得到三维实体后，利用三维软件自带的合并曲面功能，将仿真加工时产生的小曲面合并，分别得到的8阶和12阶正交变传动比面齿轮模型如图7所示.

图5 程序流程图

图6 软件界面

图7 虚拟加工模型图

3 实体加工及实验研究

3.1 实体加工

分别用三轴数控铣削加工和数控电火花线切割加工方法加工出八阶正交变传动比面齿轮和二阶非圆齿轮实体.仿真加工模型与实体如图8所示.由图8(c)可见，仿真加工模型与实体一致，表明该正交变传动比面齿轮副的参数化设计及仿真系统的正确性.

图8 实体加工

3.2 实验研究

正交变传动比面齿轮副的试验台由变频直流电动机、转速扭矩测量仪、正交变传动比面齿轮副传动箱、试验台架、变速箱综合测试系统等仪器及设备组成.传动试验台如图9所示.

图9 试验台布置

如图10所示，实验测定的实际传动比曲线和理论传动比曲线在有些部位表现出差异，导致这种差异的原因是齿轮副加工过程存在加工误差，齿轮的安装过程存在安装误差，同时，传感器采集数据本身及后期的数据处理过程也有一定的误差.但是，其变化规律基本相同，变化趋势基本一致，表明正交变传动比面齿轮副的设计及三维造型方法是可行的.

4 结 论

1) 建立了正交变传动比面齿轮啮合坐标系，由空间坐标转换原理，得出了各坐标的相互转换关系，进而推导出了正交变传动比面齿轮的节曲线、齿顶曲线以及齿根曲线的参数方程.

2) 根据共轭齿廓理论，分析了加工过程中刀具的空间走刀轨迹，推导得到了正交变传动比面齿轮的齿面参数方程.

3) 由空间齿轮啮合原理，对正交变传动比面齿轮的根切和变尖现象进行了详细的研究，得出了正交变传动比面齿轮无根切的最小内径及不产生变尖最大外径计算方法.

4) 利用Solidworks三维造型功能以及应用程序接口(API)，结合编程软件VB，开发了正交变传动比面齿轮的设计与仿真加工系统，得到了正交变传动比面齿轮的三维实体及其装配模型，实现了正交变传动比面齿轮的可视化.

5) 完成了正交变传动比面齿轮的加工，搭建了正交变传动比面齿轮副的传动实验台，通过实验研究，验证了设计分析方法及加工制造方法的正确性和可行性.

[1] LITVIN F L, ALFONSO F, MATT H． Design generation and TCA of new type of asymmetric face-gear drive with modified geometry[J]. Computer Methods in Applied Mechanics and Engineering, 2001,19(43/44):5837-5865.

[2] 王 志,石照耀,刘建炜,等.正交面齿轮计算机仿真加工[J].北京工业大学学报,2012,38(7):1004-1007.

WANG Zhi,SHI Zhao-yao,LIU Jian-wei,etal. Simulation of orthogonal face gear proceeding[J]. Journal of Beijing University of Technology,2012,38(7):1004-1007. (In Chinese)

[3] 李大庆,邓效忠,魏冰阳,等.偏置斜齿面齿轮几何设计及齿宽特性分析[J].机械设计,2011,28(9):59-62.

LI Da-qing, DENG Xiao-zhong, WEI Bing-yang,etal. Tooth geometry design and tooth width characteristics analysis of offset helical face-gear[J]. Journal of Machine Design,2011,28(9):59-62. (In Chinese)

[4] 张会会.非正交面齿轮传动设计研究[D].济南:山东大学机电工程学院,2012.

ZHANG Hui-hui.Research on the non-orthogonal face gear drive design[D].Jinan:College of Mechanical and Electrical Engineering, Shandong University,2012. (In Chinese)

[5] MICHELE G, JEAN-PIERRE D V, COLIN-YANN J. Quasi-static analysis of a face gear under torque[J]. Computer Methods in Applied Mechanics and Engineering, 2005,194(39/41): 4301-4318.

[6] FRACKOWIAK P. Modeling and cutting a face-gear with straight line on CNC milling-machine[J]. Manufacturing Engineering, 2010,9 (3):19-21.

[7] FRACKOWIAK P. Forming and geometrical dependences in the nom-homogeneous face-gear with involute line[J]. Manufacturing Engineering ,2010,9 (4): 28-30.

[8] OHSHIMA F , YOSHINO H, NADEHIRO E. A study on high reduction face gears (2nd report, cutting of face gear) [J]. Transactions of the Japan Society of Mechanical Engineers, Part C, 2009,75(758):2816-2821.

[9] WANG Yan-zhong, WU Can-hui,GONG Kang,etal. Loaded tooth contact analysis of orthogonal face-gear drives[J]. Proceedings of the Institution of Mechanical Engineers, 2012,226(9):2309-2319.

[10]ZHAO N, GUO H, FANG Z D,etal. Loaded tooth contact analysis of modified helical face gears[C]// YAN X T, EYNARD B, ION W J，etal. Global Design and Manufacture to Gain a Competitive Edge． London: Springer Verlag, 2008:45-54.

[11]LITVIN F L, ZHANG Y,WANG J C,etal. Design and geometry of face-gear drives[J]. Journal of Mechanical Design,1992,114(4): 642-647.

[12]林超,侯玉杰,龚海,等.高阶变性椭圆锥齿轮传动模式设计与分析[J].机械工程学报,2011,47(13) :131-139.

LIN Chao, HOU Yu-jie, GONG Hai,etal. Design and analysis of transmission mode for high-order deformed elliptic bevel gears[J]. Journal of Mechanical Engineering,2011, 47(13):131-139. (In Chinese)

[13]龚海.正交非圆面齿轮副的传动设计与特性分析[D].重庆:重庆大学机械工程学院,2012.

GONG Hai. Transmission design and characteristic analysis of orthogonal non-circular face gear drive[D].Chongqing: College of Mechanical Engineering, Chongqing University,2012. (In Chinese)

[14]吴序堂,王贵海.非圆齿轮及非匀速比传动[M].北京：机械工业出版社,1997:17-19.

WU Xu-tang, WANG Gui-hai. Transmission of noncircular gears and variable ratio[M].Beijing:China Machine Press,1997:17-19. (In Chinese)

[15]杨俊,谭建平,杨武,等.大型水压机阀芯驱动系统双圆弧凸轮设计及应用[J].湖南大学学报:自然科学版，2013,40(7):53-58.

YANG Jun , TAN Jian-ping, YANG Wu,etal. Design and application of cam with two arc curvein the spool opening of large water hydraulic press[J]. Journal of Hunan University：Natural Sciences,2013,40(7):53-58.(In Chinese)

[16]李特文 F L.齿轮几何学与应用理论[M].上海:上海科学技术出版社,2008:112-115.

LITVIN F L. Gear geometry and applied theory[M]. Shanghai: Shanghai Science Press, 2008:112-115. (In Chinese)