混沌云克隆选择算法及其应用＊

张英杰，赵芳芳

（湖南大学 信息科学与工程学院，湖南 长沙 410082）

免疫克隆选择算法是一种高性能优化方法，其良好的自学习和自适应能力，为函数优化等具体数学模型问题提供了很好的解决方案［1］．但传统的免疫克隆选择算法也存在一些固有缺陷，如：采用二进制编码方式的算法易出现维数灾难且搜索效率不高等问题；高斯变异虽具有较强的局部搜索能力但易陷入局部极值、在迭代后期出现停止不前等现象；柯西变异与高斯变异相比虽然更易跳出局部极值点，但在进行更精确的局部搜索方面性能降低．为此，国内外相关研究学者提出新的算子来改进算法，更好地提高算法的全局搜索能力和收敛速度［2－5］．

云模型是一种用语言值描述的某个定性概念与其定量表示之间的不确定性转换模型，同时具有随机性和稳定性，为定性与定量相结合的信息处理提供了有力手段．近年来，进化算法研究学者也对其十分关注：文献［6］利用云发生器代替遗传算法中的交叉、变异算子，提出一种云遗传算法（CGA），在函数优化中取得了良好效果；文献［7］利用云模型对粒子进化和变异进行统一建模，提出了一种云变异粒子群算法（CHPSO），该算法有较强的全局搜索能力，适用于多峰值函数的优化．

本文将云模型理论与克隆选择算法相结合，提出一种改进算法——混沌云克隆选择算法（Chaotic Cloud Clonal Selection Algorithm，CCCSA）．旨在通过引用混沌初始化，以提高群体的质量；利用基本云发生器产生的云算子实现变异操作，改善抗体的多样性，以达到总体提高算法优化性能的目的．

1 算法改进与设计

假定连续优化问题可描述为式（1）形式：

式中：抗原对应于f（x），其为n维解空间S上的连续实函数；抗体xi对应于解的值；函数值对应于抗体和抗原的亲和度．其中，抗体xi采用十进制编码方式以提高算法的求解精度与增大搜索空间．

1．1 混沌初始化算子

一般的混沌初始化算法的思想是：首先产生一定量的混沌序列进行全局搜索，再对搜索结果进行排序，从中择优选择初始化群体，这样有助于求解效率的提高和解质量的改善［8］．本文采用混沌序列中的Logistic映射来初始化种群．典型的一维Logistic映射表达式如式（2）所示［9］：

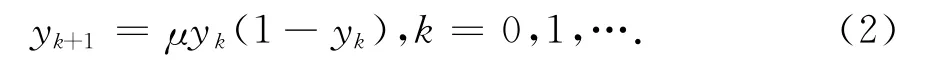
式中：k为迭代次数；μ为控制系统混沌行为的参数，其取值区间为（0，r］，当μ＝4，控制系统呈现出完全的混沌状态；yk为混沌变量；y0∈（0，1）是混沌变量的初始值，且y0≠0．5．

这里，D 维的混沌向量Yi可描述为式（3）：

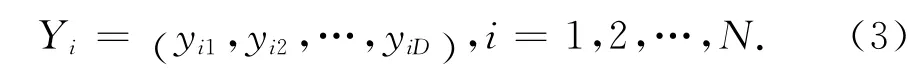
式中：优化变量xi由式（4）计算生成：

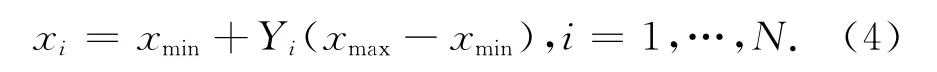
计算目标函数值，从N个初始群体中选择性能较好的m个解作为初始解，即随机产生m个初始抗体．

1．2 云变异算子

为了提高克隆选择算法的动态寻优性能及变异的有效性，本文利用云模型云滴的随机性和稳定倾向性特点，由云模型基本云发生器算法实现变异操作．随机性可以保持个体多样性从而避免搜索陷入局部极值，而稳定倾向性又可以很好地保护较优个体从而对全局最优值进行自适应定位［10］．云变异算子实现算法可描述为：

Step 1Ex＝xi，（xi为抗体），

Step 2En＝（xmax（j）－xmin（j））／c1，

Step 3He＝En／c2，

Step 4 执行正态云的基本生成算法，并生成随机数Temp，更新抗体．

其中，Ex代表父本抗体的优良特征；En代表抗体变异的大概范围；He决定抗体变异的离散程度，表征进化的稳定性，He过大，会在一定程度上丧失“稳定倾向性”，He过小，又在一定程度上丧失”随机性”；xmax（j），xmin（j）分别为第j维变量的最大值与最小值．兼顾算法的效率和精度，本文实验取c1＝2．9，c2＝10．

1．3 其他算子

1）克隆选择算子

在算法进化过程中，遵循亲和度较高的个体被遗传到下一代的概率较大而亲和度较低的个体被遗传到下一代的概率较小的原则，故选择克隆算子如式（5）所示：

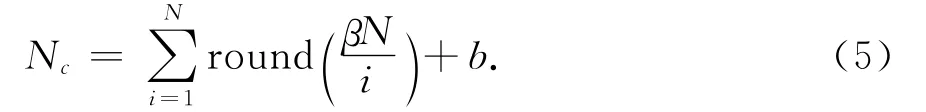
式中：Nc为克隆后的抗体群规模；β为克隆系数，用来控制克隆的规模；round为取整函数；b为大于1的常数以确保每个抗体都存在一定数量的克隆个体．按此算子进行克隆操作，算法可在很大程度上使高亲和力抗体中的优秀基因得以更好的保存和发展．

2）克隆抑制算子

采用精英保留策略，对进化结果进行有选择的抑制操作．克隆算子操作的源抗体与克隆抗体经变异算子作用后得到的临时抗体群共同形成一个集合Ab′，克隆抑制算子对抗体群Ab′进行再选择，抑制亲和度低的抗体，保留亲和度高的抗体进入新的抗体种群，该操作有利于加强算法的局部搜索能力．

3）种群更新算子

种群更新操作是对种群中亲和度较低的抗体进行更新，从抗体种群中删除这些抗体并用混沌算法生成的新抗体替代．该操作有利于保持抗体的多样性、探索新的可行解空间区域与加强全局搜索能力．

2 改进算法的实现步骤

Step 1 解初始化．采用混沌算法生成种群规模为N的初始种群Ab′；

Step 2 评价机制．对种群中的每一个可行解进行适应度评价，并按亲和度从大到小进行排序；

Step 3 终止判断．判断是否满足算法终止条件（当前进化代数大于最大迭代代数或函数值达到所接受的精度），若满足，则输出计算结果并终止；否则，继续寻优运算；

Step 4 免疫选择．选择m个亲和度较高的抗体形成免疫记忆库M；

Step 5 克隆操作．对记忆库M中的每个抗体按克隆算子进行克隆，得到克隆抗体群Abc；

Step 6 变异操作．对Abc抗体群中每个抗体按照云变异算子进行变异，得到变异抗体群Abm；

Step 7 抑制操作．删除Ab，Abm抗体群中亲和度较低的抗体，得到抗体群Abs；

Step 8 更新操作．用混沌算法生成的n个新的抗体替代Abs中亲和度较低的抗体，返回Step 3．

3 经典函数测试

采用文献［7］中的16个经典函数进行测试．实验参数设置为：种群大小为100，最大迭代代数为1 000，每个函数独立运行30 次．CGA 数据来自于文献［6］，CHPSO 数据来自于文献［7］．实验结果如表1所示．

表1中，参考值是指函数的理论最小值，平均代数是指最佳适应度与参考适应度之差的绝对值小于10－3时，其进化代数多次独立实验的平均值，‘－’表示在1 000次迭代后最佳值实验结果不理想，所以未计算其最佳值、平均值和平均代数．

CCCSA 利用了基于抗体的免疫进化机制和正态云模型的稳定倾向性、随机性以及混沌的遍历性特点．稳定倾向性能较好地保护最优抗体从而实现对最优值的自适应定位，随机性能保持个体多样性从而有效地防止算法陷入局部极值，遍历性能提高初始种群的质量从而加快算法的收敛速度．由表1可知，除F7，F15和F16这些高维、变量范围较大的函数外，CCCSA 对其余函数的算法性能明显优于CGA；综合算法精度和收敛速度，CCCSA 整体性能优于CHPSO 算法．

表1 CCCSA ＆CGA，CHPSO 优化结果比较Tab．1 The comparison of CCCSA ＆CGA，CHPSO on function test

4 CCCSA应用－ADRC参数优化整定

4．1 自抗扰控制理论

自抗扰控制器是由我国学者韩京清提出的新一代非线性控制器，简称ADRC［11－12］．其基本结构如图1 所示．可见，ADRC 主要由跟踪微分器TD（Tracking Differentiator）、扩 张 状 态 观 测 器ESO（Extended Stte Observer）和非线性状态误差反馈控制律NLSEF（Non－Linear State Error Feedback）3部分构成，是在汲取经典PID 不依赖于对象模型的思想精髓基础上，改进经典PID 固有缺陷而形成的新型控制器．

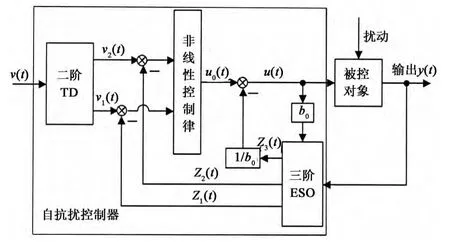
图1 自抗扰控制的基本结构Fig．1 The structure diagram of the ADRC

这种控制器只需要对象的输入u、输出y和控制器的目标值，不依靠受控对象的精确模型，因此更适应于广泛地控制工程实践．但自抗扰控制器进行参数整定时，需要设置参数β01，β02，β03，β1，β2，参数众多难以调整，制约了这一优良控制器在工程中的广泛应用，因此，ADRC的参优化整定也成为自抗扰控制理论的研究热点［13］．鉴于此，本文将改进算法CCCSA应用到自抗扰控制器参数优化整定中，期望进一步提高控制系统的调节精度和抗干扰性能．

4．2 实验对象及适应度函数

为验证本文算法对ADRC 参数优化整定的有效性选取如式（6）所示的时滞对象［11］：

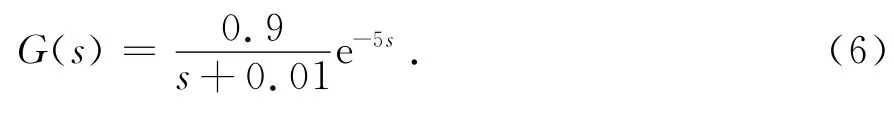
该对象由于纯迟延的存在，因此当对象受到干扰而引起被调量改变时，控制器产生的控制作用不能即时对干扰产生抑制作用．含有纯滞后环节的闭环抵制系统必然存在较大的超调量和较长的调节时间［1 4］．

因此，为了获取满意的控制效果和过渡过程的动态特性，同时为了解决控制量过大和超调量较大的问题，采用式（7）的适应度评价函数：

式中：e（t）为系统误差，u（t）为控制器输出，tu为上升时间．在该实验中，采样时间取为0．1s，输入令为单位阶跃信号，权值w1＝0．999，w2＝0．015，w3＝2，w4＝100．设置ADRC 控制器的时滞系数，TD 的快慢因子r0取800，滤波因子h0取1，控制器的非线性系数［α01，α02］为［0．75，1．25］，ESO 的非线性系数取［0．5，0．25］，线性区间δ取0．01，参数β1，β2的取值范围为［0，1］，参数β01，β02，β03的取值范围为［0，50］．

4．3 仿真实验

实验1 阶跃响应

对系统施加一个单位阶跃输入信号，采用本文算法CCCSA，PSO［11］和CSA［15］3种优化算法得到的控制器参数见表2，仿真结果如图2、图3所示．由图2和图3可知，经CCCSA算法整定参数的二阶自抗扰控制器具有更好的控制效果，其控制的滞后系统的性能指标（上升时间，超调量和稳态误差）远远优于PSO 算法以及CSA整定的自抗扰控制器．

表2 3种算法阶跃响应实验性能指标Tab．2 The parameter of ADRC＿step＿response

实验2 抗扰动测试

在系统的输入通道中加入一个幅值为0．1的方波（35s～40s）扰动，仿真结果如图4 和图5 所示．由图4 和图5 可知，CCCSA 优化的控制系统与PSO、CSA 优化的控制系统相比，系统在40s后出现的波动更小，且系统能较快的重新回到稳态．

实验3 鲁棒性实验

采用Monte－Carlo方法定量比较采用CCCSA方法整定的ADRC 和采用PSO，CSA 方法整定的ADRC的鲁棒性．这里只给出了系统模型的比例参数在－20%～20%内随机摄动的情形．根据单位阶跃定值响应，计算ts，σ% 和ITAE，重复实验1 000次，仿真结果如表3和图6所示．由表3可知，CCCSA 的各项指标明显优于PSO 和CSA．显然，通过CCCSA 优化整定参数的自抗扰控制器具有更强的鲁棒性．

由上述实验可知，在相同的输入给定作用下，本文算法整定的控制系统具有更优良的控制性能以及较强的抗干扰性能．

图5 局部精细曲线Fig．5 The local refined curve

图2 目标收敛曲线Fig．2 The objective function convergence curve

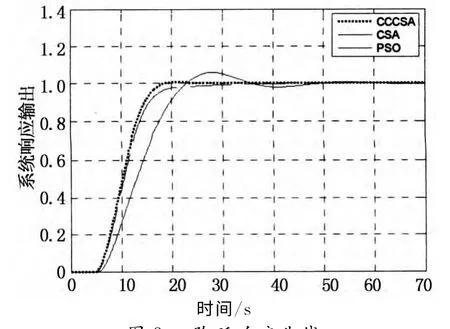
图3 阶跃响应曲线Fig．3 The step response curve

图4 扰动后的阶跃响应曲线Fig．4 The step response curve

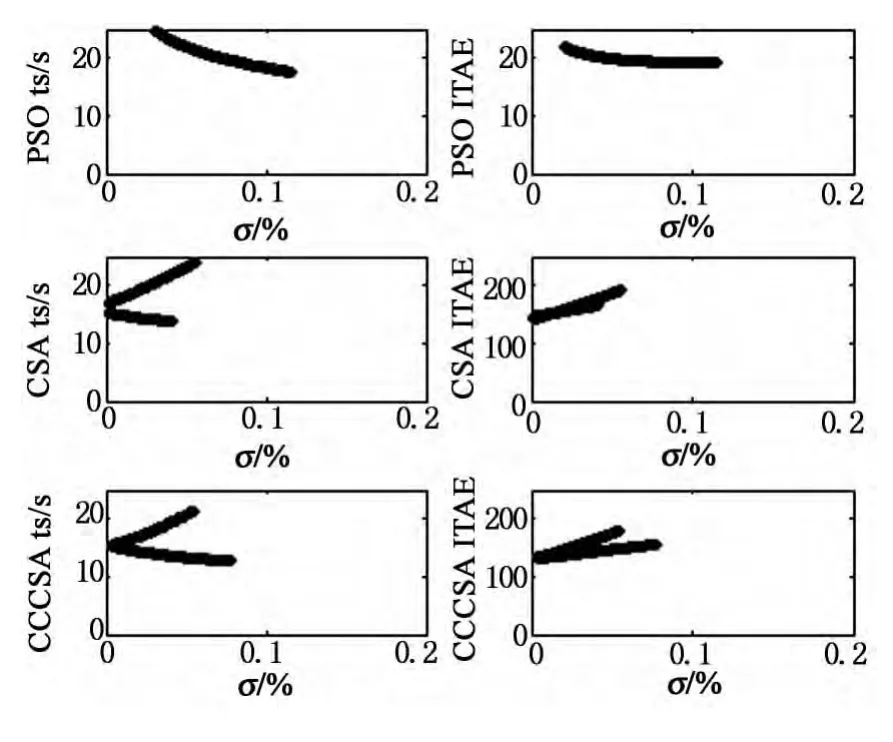
图6 3种算法整定的控制系统鲁棒性比较Fig．6 The compare of robustness

表3 自抗扰控制器鲁棒性实验性能指标Tab．3 Roubustness of performance for adjusted ADRC

传统的克隆选择算法在函数优化寻优已表现出良好的算法性能，但也存在一些固有的缺陷．本文利用云模型云滴的随机性和稳定倾向性以及混沌系统的随机性、遍历性，提出一种混沌云克隆选择算法（CCCSA）．该算法的主要思想是通过利用混沌遍历性产生初始种群，由云模型基本云发生器实现免疫算法中的变异算子，完成进化过程，实现改善算法整体性能的目的．

经典函数测试实验结果，验证本文算法有较快的收敛速度，较强的全局搜索能力和较好的鲁棒性．在以时滞系统为受控对象的ADRC 参数整定优化应用实例中，优化的控制系统具有优良的控制性能与鲁棒性以及较强的抗干扰能力，进一步验证了该算法的有效性．

［1］DE CASTRO L N，ZUBEN F V．The clonal selection algorithm with engineering applications［C］／／Procedings of the Gentetic and Evolutionary Computation Conference，Workshop on Artificial Immune Systems and Their Applications，July，2000：36－37．

［2］杨明慧，彭玉楼，傅明．实数编码的克隆选择算法的网络入侵检测［J］．计算机工程与应用，2005，10（28）：135－136．

YANG Ming－hui， PENG Yu－lou， FU Ming． Network intrusion detection based on real coded clone selection algorithm ［J］．Computer Engineering and Applications，2005，10（28）：135－136．（In Chinese）

［3］陶新民，刘福荣，刘玉，等．定向多尺度变异克隆选择优化算法［J］．控制与决策，2011，2（26）：175－181．

TAO Xin－min，LIU Fu－rong，LIU Yu，etal．Clone selection optimization algorithm with directional multi－scale mutation［J］．Control and Decision，2011，2（26）：175－181．（In Chinese）

［4］邓雪峰，唐俊．一种新型的克隆选择算法［J］．计算机应用研究，2011，28（1）：332－334．

DENG Xue－feng，TANG Jun．Novel clone selection algorithm［J］．Application Research of Computers，2011，28（1）：332－334．（In Chinese）

［5］宋丹，赖旭芝，吴敏．基于等级变异的克隆选择算法［J］．模式识别与人工智能，2011，24（3）：438－443．

SONG Dan，LAI Xu－zhi，WU Min．Clonal selection algorithm based on grade variation［J］．PR ＆AI，2011，24（3）：438－443．（In Chinese）

［6］戴朝华，朱云芳，陈维荣，等．云遗传算法及其应用［J］．电子学报，2007，35（7）：1419－1424．

DAI Chao－hua，ZHU Yun－fang，CHEN Wei－rong，etal．Cloud model based genetic algorithm and its applications［J］．Acta Electronica Sinica，2007，35（7）：1419 － 1424．（In Chinese）

［7］张英杰，邵岁峰，JULIUS N．一种基于云模型的云变异粒子群算法［J］．模式识别与人工智能，2011，24（1）：90－96．ZHANG Ying－jie，SHAO Sun－feng，JULIUS N．Cloud hypermutat－ion particle swarm optimization algorithm ［J］．PR ＆AI，2011，24（1）：90－96．（In Chinese）

［8］KANSO A，SMAOUI N．Logistic chaotic maps for binary numbers generations［J］．Chaos Solitons ＆ Fractals，2009，40（5）：2557－2568．

［9］王兴元，王明军．二维Logistic映射的混沌控制［J］．物理学报，2008，2（57）：731－736．

WANG Xing－yuan，WANG Ming－jun．Chaotic control of the coupled Logistic map［J］．Acta Phys Sin，2008，2（57）：731－736．（In Chinese）

［10］ 张光卫，何锐，刘禹，等．基于云模型的进化算法［J］．计算机学报，2008，31（7）：1082－1091．

ZHANG Gong－wei，HE Rui，LIU Yu，etal．An evolutionary algorithm based on cloud model ［J］．Chinese Journal of Computers，2008，31（7）：1082－1091．（In Chinese）

［11］ 史永丽，侯朝桢，苏海滨．基于粒子群优化算法的自抗扰控制器设计［J］．系统仿真学报，2008，20（2）：433－436．

SHI Yong－li，HOU Chao－zhen，SU Hai－bin．Autodisturbance rejection controller design based on particle swarm optimization algorithm ［J］．Journal of System Simulation，2008，20（2）：433－436．（In Chinese）

［12］ 刘朝华，张英杰，章兢，等．基于免疫双态微粒群的混沌系统自抗扰控制［J］．物理学报，2011，60（1）：1－9．

LIU Zhao－hua，ZHANG Ying－jie，ZHANG Jing，etal．Active disturbance rejection control of a chaotic system based on immune binary－state particle swarm optimization algorithm［J］．Acta Phys Sin，2011，60（1）：1－9．（In Chinese）

［13］ 孙亮，吴根忠．自抗扰控制器优化设计及其应用［J］．系统电机与控制应用，2010，37（3）：26－30．

SUN Liang，WU Gen－zhong．Application and optimize design of active disturbance rejection controller ［J］．Motor and Control Application，2010，37（3）：26－30．（In Chinese）

［14］ 韩京清．时滞对象的自抗扰控制 ［J］．控制工程，2008，15（1）：7－11．

HAN Jing－qing． Auto－disturbances rejection control for time－delay systems［J］．Control Engineering of China，2008，15（1）：7－11．（In Chinese）

［15］ 任海鹏，朱峰．基干免疫克隆选择算法的无刷直流电动机速度自抗扰控制器优化设计 ［J］．电机与控制学报，2010，14（9）：69－74．

REN Hai－peng，ZHU Feng．Optimal design of speed adaptive disturbance rejection controller for brushless DC motor based on immune clonal selection algorithms［J］．Electric Machines and Control，2010，14（9）：69－74．（In Chinese）