基于热流分析的搅拌摩擦焊接工艺参数

冯天涛，张晓辉

（山东农业大学 山东省园艺机械与装备重点实验室，山东 泰安 271018）

0 前言

搅拌摩擦焊FSW（friction stir welding）是一种固相连接新技术，与传统焊接方法相比，优势明显，可以用来焊接很多过去认为难以焊接的金属。为了更好地理解FSW工艺过程，国内外学者在过去的十几年中建立了很多解析和数值模型，根据它们的应用范围和物理假设可分为三类：热传输模型[1-5]、基于固体力学的热力分析模型[6-9]和基于流体力学的热流分析模型[10-14]。热传输模型主要通过构建不同形式的热源求解热传导方程来预测工件温度场的分布，而温度与接头的组织和性能是密切相关的。热力分析模型将热传输模型得到的温度场与工件的受力进行耦合来预测工件的残余应力与残余变形。上述两类模型在求解温度场的过程中均没有考虑材料流动的影响。热流分析模型将FSW过程中的固体材料认为是流体，通过求解连续性方程、动量方程和能量方程获得包含对流传热影响的温度场、速度场及压力场等相关信息。

FSW过程工艺参数是搅拌头的旋转速度、工件移动速度（焊接速度）和下压量（或轴向压力）；响应参数主要是峰值温度、作用于搅拌针上的纵向力（与焊接速度反向）和扭矩[15]。焊接过程首先要获得性能良好的接头，同时希望效率高、能耗少且搅拌头使用时间长。实现高效率就要提高焊接速度，FSW过程中随着焊接速度的提高，搅拌针折断的可能性增加，使用寿命缩短，提高搅拌头的旋转速度会缓解这一矛盾，但能耗会增加。所以，选择合理的工艺参数具有十分重要的实际意义。

本研究利用热流分析模型分析FSW过程中随旋转速度和焊接速度的变化，峰值温度与纵向力的变化趋势，以期为焊接工艺参数的选择提供依据。热流分析过程中必须考虑搅拌头周围材料流动的影响，而其速度大小与搅拌头和工件的接触条件有关，接触系数越大，搅拌头周围材料流动速度越快，在此对随接触系数的变化，峰值温度与纵向力的变化趋势也进行了研究。

1 热流分析模型

本研究将FSW过程中的材料看作是绕过旋转圆柱体的层流、粘性、非牛顿流体，通过求解流体的连续性方程、动量方程和能量方程分析准稳态时的热流耦合情况。

焊接过程的热输入来自于搅拌头与工件接触区域的摩擦摩擦产热和塑性变形产热，当达到准稳态时，接触区域的任一点的摩擦剪应力等于材料发生塑性变形时的剪应力[5]。分析时，轴肩、搅拌针侧面和底面与工件在接触区域所产生的热量均予以考虑。

轴肩与工件在接触区域由于摩擦和塑性变形而产生的热量可表示为

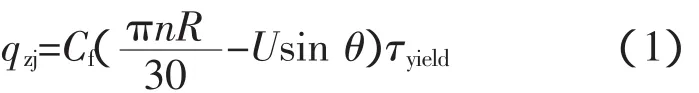
搅拌针侧面与工件在接触区域由于摩擦和塑性变形而产生的热输入可表示为

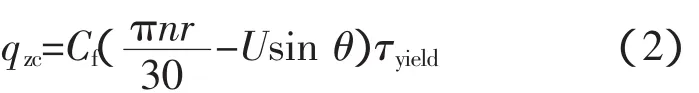
式中 Cf为搅拌头与工件在接触区域产生的热量传入工件的比例，在此取为0.85；n为搅拌头的旋转速度；U为工件运动速度（焊接速度与其大小相等，方向相反）；R为轴肩与工件的接触区域上任意一点到搅拌头旋转轴线的距离；r为搅拌针的半径；θ为搅拌头与工件的接触区域上任意一点与旋转轴线的连线与工件运动方向的夹角；τyield为材料发生屈服时的剪切应力。

搅拌针底面与工件在接触区域由于摩擦和塑性变形而产生的热输入与式（1）相同。

工件与搅拌头的接触条件认为是部分滑移粘着状态[2]，接触系数取为0.65[16]。τyield与屈服强度的关系见式（3），而材料的屈服强度随温度的上升而减小[5]，当温度达到一定值后，屈服强度减少为0，搅拌头与工件的接触区域就不再产生热量，温度就不再上升。

在此选用6061铝合金，熔点为855 K，密度随温度变化较小，取为2 700 kg/m3，将导热系数λ、比热Cp和屈服强度σs随温度变化的数据[14]分别拟合为

2 模拟过程

FSW过程中搅拌头垂直于工件，轴肩是一个平面，直径26 mm；搅拌针为光滑圆柱体，直径5.9 mm，长度5.6 mm；搅拌头作逆时针旋转运动，转速600 r/min，工件自左向右沿x正方向匀速运动，速度90 mm/min。为节省计算时间，只取工件的一部分进行计算，计算区域为一圆柱形区域，x方向为52 mm，即两倍的轴肩直径，z方向为50 mm，y方向为板厚6.3 mm，如图1所示。

图1 计算区域示意Fig.1 Schematic of computational zone

轴肩、搅拌针侧面及底面为热输入边界，其热流量见式（1）、式（2）。上表面、下表面、前进侧和后退侧的边界均设置为移动墙，速度与工件运动速度相同。流体入口边界设置为速度入口边界条件，且速度等于工件运动速度，流体出口边界设置为压力出口边界条件。上表面暴露于空气中，是一种热对流边界，热对流系数取为50 W/（m2·K）；下表面与垫板接触，热传导系数取为500 W/（m2·K）；前进侧和后退侧部分与空气接触，部分与夹具接触，设置其热传导对流系数取为200 W/（m2·K），初始温度设为300 K。

对计算区域利用Gambit建模、划分网格并导入计算流体力学软件Fluent，采用隐式、线性、分离解算器进行计算并对网格进行离散。在求解过程中，应用标准离散方程计算压力，应用二阶逆风方程计算动量方程，应用一阶逆风方程计算能量方程。

为分析工艺参数变化对响应参数的影响，以文献[14-16]中的焊接速度和旋转速度进行计算，其他参数不变，共20个算例。焊接速度为：0.5 mm/s、1 mm/s、1.5 mm/s和 2 mm/s，旋转速度为：200 r/min、400 r/min、600 r/min、800 r/min 和 1 000 r/min。

为分析接触系数对响应参数的影响，以恒定的焊接速度和旋转速度进行计算，共5个算例。焊接速度为1.5 mm/s，搅拌头旋转速度为600 r/min，接触系数分别取 0.1、0.3、0.65、0.85 和 1。

3 结果与分析

3.1 温度场和速度场分布

经搅拌头的轴线将计算的温度场沿纵向切片如图2所示，计算表明峰值温度为759 K，约为6061铝合金熔点的89%。垂直于搅拌头的轴线将计算的速度场沿横向切片如图3所示。该算例采用的参数是：旋转速度600 r/min，焊接速度1.5 mm/s，接触系数0.65。

图2 热流模型计算的温度分布Fig.2 Contour of temperature computed by thermal and fluid model

3.2 旋转速度对峰值温度的影响

焊接速度为1.5 mm/s时不同旋转速度对应的峰值温度如图4所示。由图4可知，在旋转速度较小时，随着旋转速度的增加，峰值温度增加较为明显，当旋转速度增加到600 r/min以后，峰值温度基本保持稳定，这是因为在焊接速度、搅拌头尺寸一定的情况下，焊接过程热输入与旋转速度和材料的最大剪切应力有关，随着旋转速度的提高，一方面材料温度升高，另一方面温度升高又使材料的最大剪切应力减小，在两者的综合作用下，焊接热输入保持基本不变，因而峰值温度也就维持恒定。

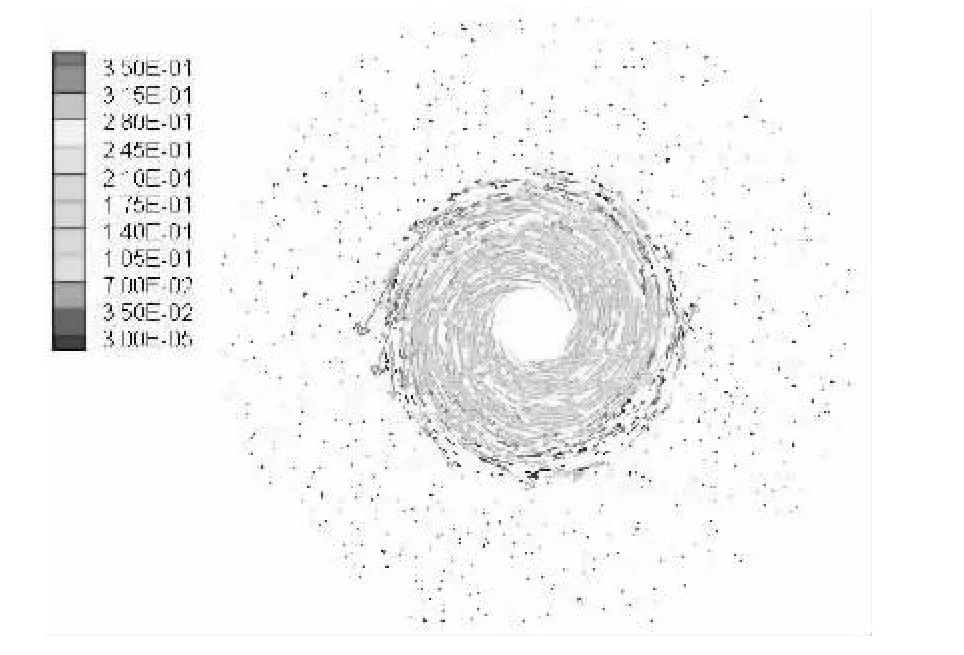
图3 热流模型计算的速度矢量Fig.3 Vector of velocity computed by thermal and fluid model

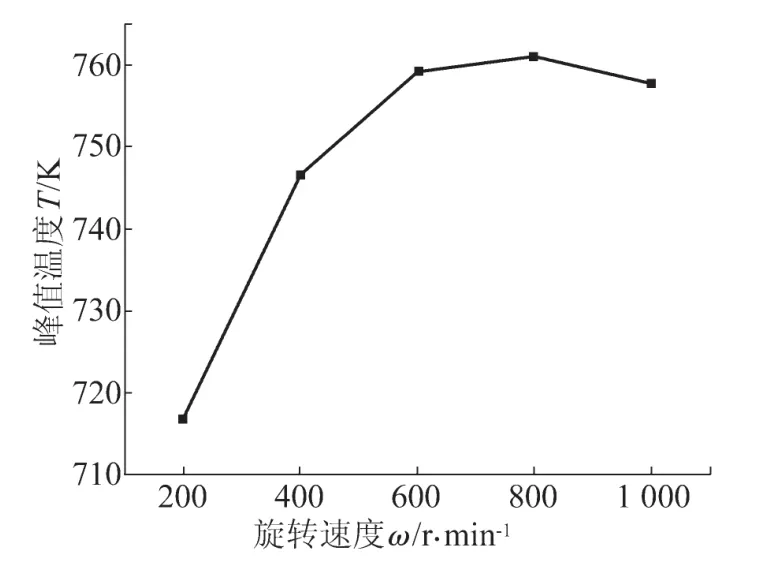
图4 不同旋转速度对峰值温度的影响Fig.4 Effect of different rotating speed on peak temperature

3.3 旋转速度对纵向力的影响

焊接速度为1.5 mm/s时不同旋转速度对应的纵向力如图5所示。由图5可知，随着旋转速度的增加，纵向力逐渐减小，且曲线趋于平缓。这是因为随着旋转速度的增加，焊接热输入不断增加，材料温度和应变率升高，流动应力下降，搅拌头前进的阻力减小。但搅拌头的旋转速度增加到一定程度，温度不会继续升高，应变率则随旋转速度的增加而继续变大，而使流动应力下降的速率减缓。从工具使用寿命考虑，应采用大的旋转速度，但耗能会增加。

3.4 焊接速度对峰值温度的影响

旋转速度为600 r/min时不同焊接速度对应的峰值温度如图6所示。由图6可知，焊接速度对峰值温度的影响很小，且没有明显的规律可循，这是因为FSW过程中焊接速度与搅拌头的线速度相比太小，焊接速度的变化对焊接过程的热输入影响甚微。

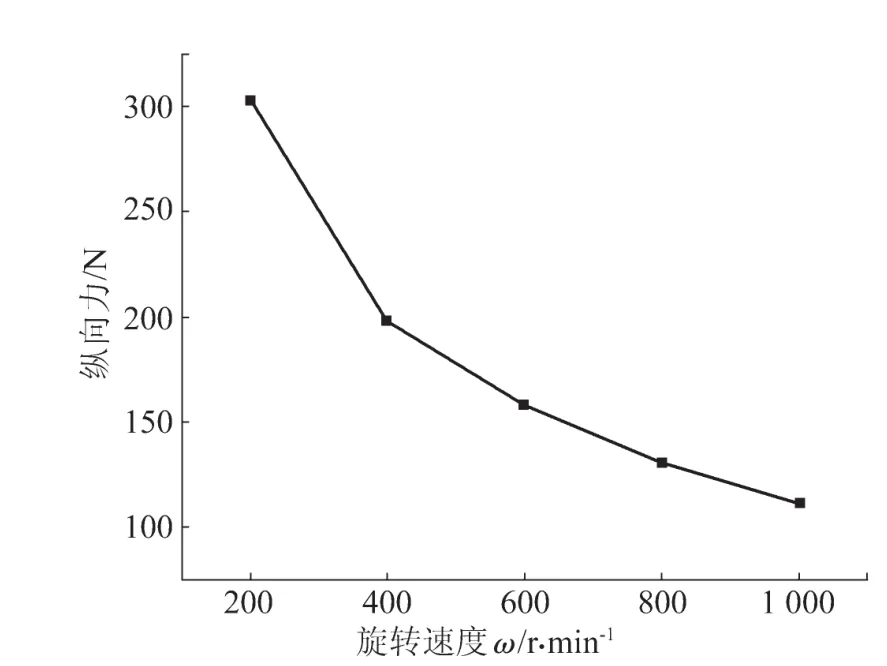
图5 不同旋转速度对纵向力的影响Fig.5 Effectofdifferentrotatingspeedonlongitudinalforce

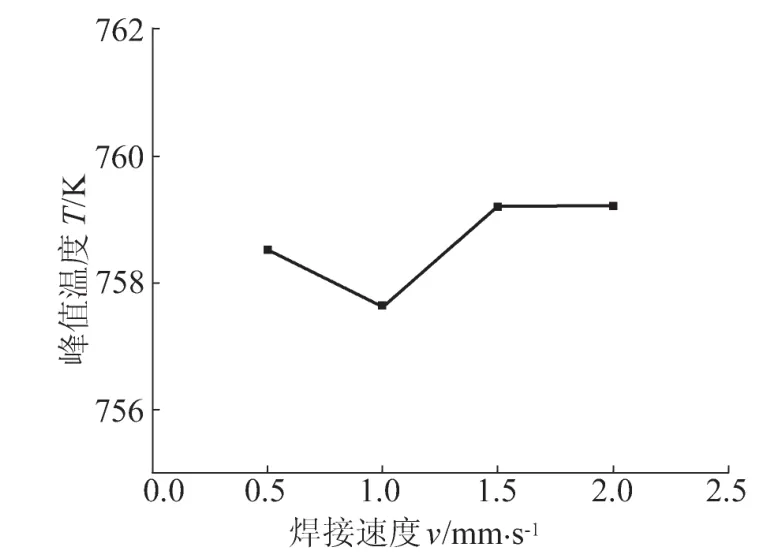
图6 不同焊接速度对峰值温度的影响Fig.6 Effect of different welding speed on peak temperature

3.5 焊接速度对纵向力的影响

旋转速度为600 r/min时不同焊接速度对应的纵向力如图7所示，由图7可知，随着焊接速度的增加，纵向力线性增加。这是因为随着焊接速度的增加，搅拌头前方需要转移到后部的材料层变厚，而使搅拌头前进的阻力增大。从工具使用寿命考虑，应采用小的焊接速度，但生产效率会降低。

从生产角度出发，希望在保证质量的前提下，提高生产效率，降低能耗，延长工具使用寿命，所以在焊接工艺参数选择时必须综合考虑。不能一味为提高生产效率而提高焊接速度，如果采用大的焊接速度，一定要以大的转速相配合，否则，即使可以得到性能良好的接头，搅拌头的使用寿命也会大大降低。但转速不要过高，一是能耗问题，二是因为在焊接速度一定的情况下，转速超过一定值，峰值温度基本不变，纵向力的减小趋势也会减缓。

3.6接触系数对峰值温度的影响

图7 不同焊接速度对纵向力的影响Fig.7 Effectofdifferentweldingspeedonlongitudinalforce

当接触系数为0时，搅拌头与工件之间是纯滑移，搅拌头周围的材料不运动，热量仅有摩擦产生；当接触系数为1时，搅拌头与工件之间是纯粘着，搅拌头周围的材料以与搅拌头相同的转速旋转，热量仅有材料的塑性变形产生。不同接触系数对峰值温度的影响如图8所示，由图8可知，在接触系数由小变大的过程中，峰值温度不断减小，只是在系数较小时峰值温度有所上升。这是因为接触系数较小时，搅拌头周围的材料运动较为缓慢，这部分材料由于塑性变形会产生一部分热量，另外也会由于塑性变形材料的“润滑”作用减少摩擦产热，塑性变形热和摩擦热相互叠加使温度升高。但随接触系数变大，塑性变形材料的润滑效果越来越明显，由摩擦产生的热量大幅减少，焊接热输入主要来自于材料的塑性变形产热，两者叠加使峰值温度下降。

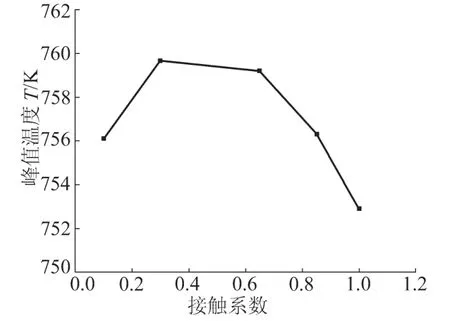
图8 不同接触系数对峰值温度的影响Fig.8 Effect of different contact coefficient on peak temperature

3.6 接触系数对纵向力的影响

不同接触系数对纵向力的影响如图9所示。由图9可知，随着接触系数由小变大，纵向力逐渐减小，但系数超过0.6以后，纵向力变化不大。这是因为随着接触系数的增大，搅拌头周围材料的运动速度变大，流动应力减小，从而使搅拌头前进的阻力减小。而系数超过0.6后，虽然运动速度在增大，但温度在降低，两者的综合作用使流动应力基本不变，因此搅拌头前进的阻力变化不大。

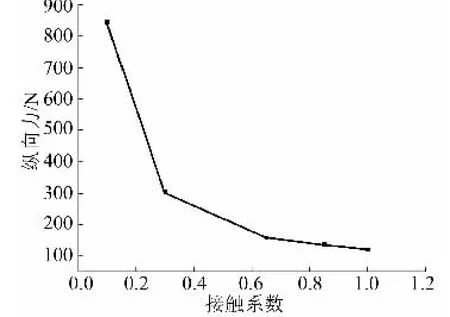
图9 不同接触系数对纵向力的影响Fig.9 Effect of different contact coefficient on longitudinal force

4 结论

（1）建立了铝合金滚筒筒体搅拌摩擦焊接过程的热流分析模型，并利用模型分析了焊接工艺参数与响应参数的关系。

（2）选取了生产中常用的参数范围：旋转速度200～1 000 r/min，焊接速度 0.5～2 mm/s进行分析。旋转速度对峰值温度和纵向力影响较大，但趋势相反，旋转速度增加使峰值温度上升而纵向力下降。焊接速度增大使纵向力线性上升，但对峰值温度影响较小，且没有明显的规律可循。

（3）利用接触系数研究了搅拌头周围材料运动速度对峰值温度和而纵向力的影响。

：

[1]SONG M，KOVACEVIC R.Thermal modeling of friction stir welding in a moving coordinate system and its validation[J].International Journal of Machine Tools&Manufacture，2003（43）：605-615.

[2]SCHMIDT H，HATTEL J.Modeling heat flow around tool probe in friction stir welding[J].Science and Technology of Welding and Joining，2005，10（2）：176-186.

[3]李红克，史清宇，赵海燕，等.热量自适应搅拌摩擦焊热源模型[J].焊接学报，2006，27（11）：81-85.

[4]COLEGROVE P A，SHERCLIFF H R，ZETTLER R.Model for predicting heat generation and temperature in friction stir welding from the material properties[J].Science and Technology of Welding and Joining，2007，12（4）：284-297.[5]SCHMIDT H B，HATTEL J H.Thermal modeling of friction stir welding[J].Scripta Materialia，2008（58）：332-337.

[6]CHEN C M，KOVACEVIC R.Finite element modeling of friction stir welding—thermal and thermo mechanical analysis[J].International Journal of Machine Tools&Manufacture，2003（43）：1319-1326.

[7]DENG X M，XU S W.Two-Dimensional Finite Element Simulation of Material Flow in the Friction Stir Welding Process[J].Journal of Manufacturing Processes，2004，6（2）：125-133.

[8]SOUNDARARAJAN V，ZEKOVIC S，KOVACEVIC R.The rmo-mechanical model with adaptive boundary conditions for friction stir welding of Al 6061[J].International Journal of Machine Tools&Manufacture，2005（45）：1577-1587.

[9]鄢东洋，史清宇，吴爱萍，等.搅拌摩擦焊接的热力耦合分析模型[J].机械工程学报，2010，46（16）：106-112.

[10]SEIDEL T U，REYNOLDS A P.Two-dimensional friction stir welding process model based on fluid mechanics[J].Science and Technology of Welding and Joining，2003，8（3）：175-183.

[11]ULYSSE P.Three-dimensional modeling of the friction stirwelding process[J].International Journal of Machine Tools&Manufacture，2002（42）：1549-1557.

[12]NANDAN R，ROY G G，DEBROY T.Numerical simulation of three-dimensional heat transfer and plastic flow during friction stir welding[J].Metallurgical and materials transactions A，2006，37A（4）：1247-1259.

[13]赵衍华，林三宝，贺紫秋，等.2014铝合金搅拌摩擦焊接过程的数值模拟[J].机械工程学报，2006，42（7）：92-97.

[14]NANDAN R，Roy G G，LIENERT T J，DEBROY T.Threedimensional heat and material?ow during friction stir welding of mild steel[J].Acta Materialia，2007（55）：883-895.

[15]LONG T，REYNOLDS A P.Parametric studies of friction stir welding by commercial fluid dynamics simulation[J].Science and Technology of Welding and Joining，2006，11（2）：200-208.

[16]ATHARIFAR H，LIN D，KOVACEVIC R.Numerical and experimental investigations on the loads carried by the tool during friction stir welding[J].Journal of Materials Engineering and Performance，2009，18（4）：339-350.