基于节点状态输出的动力学网络的自适应同步*
肖玉柱 唐素芳
(1.长安大学理学院数学与信息科学系,710086 西安)(2.西安财经学院统计学院应用数学系,710100 西安)
基于节点状态输出的动力学网络的自适应同步*
肖玉柱1†唐素芳2
(1.长安大学理学院数学与信息科学系,710086 西安)(2.西安财经学院统计学院应用数学系,710100 西安)
基于微分方程不变原理,针对带有一般耦合函数的动力学网络,设计了实现网络同步的自适应同步方法.与其它的自适应同步方法相比较,该方法的优点是利用网络的一个节点的状态作为控制目标轨道来设计控制器.这一改进可以降低控制系统的维数,并且减少控制过程中各节点间的信息传递量.最后,通过一些数值算例验证所设计控制方法的有效性.
自适应控制, 动力学网络, 复杂网络, 混沌系统, 同步
引言
自Pecora和Carroll在混沌同步方面的先驱工作[1],同步已成为非线性科学研究领域的一个重要课题.到目前为止,针对两个耦合混沌系统,学者们已经提出了很多有效的控制方法,如非线性控制[2]、自适应控制[3]、主动控制[4]等等.实际上,很多实际系统都应该由多个节点构成的具有复杂结构的动力学网络来描述,如:生物系统、神经系统和社会系统等[5].由于很多自然现象都可以通过动力学网络的同步来解释,因此动力学网络同步的研究吸引了不同领域学者们的观注.针对动力学网络的同步问题,学者们已经提出了一些有效的分析方法,如“主函数法 (master stability function method)[6]”、“连接图方法 (connection graph stability method)[7]”,以及Lu等提出的新方法[8].利用这些分析方法,学者们研究了具有不同复杂结构的动力学网络同步的条件[6-10].另一方面,现实中的网络不可避免要受到各种外界因素的影响,因此实际中网络的各节点很难自发地达到同步.为了实现实际中网络各节点间的同步,学者们已经提出了一系列有效的方法.在文献[11,12]中,作者们研究了如何利用牵制控制(pinning control)实现网络的同步.在牵制控制中,只选择网络的部分节点施加控制,因此牵制控制是实现网络同步最合适方法,但在网络结构未知的情况下,如何选折哪个节点施加控制还是一个没解决的问题.由于脉冲控制的结构简单,学者们研究了实现动力学网络同步的脉冲控制方法[13,14].由于自适应控制的反应快速和自动性,学者们提出了一些实现网络同步的自适应控制方法[15,16].上述的这些控制方法都非常有效,利用这些控制方法可以实现节点系统为混沌系统,网络结构未知的复杂动力学网络的各节点间的同步.然而,这些控制方法以节点系统的一个解作为控制目标轨道,因此要利用这些控制方法,必须事先得到节点系统的一个解.但在很多实际情况中很难得到节点系统的一个解,例如网络不存在孤立节点且节点系统的具体结构未知.为了解决上述问题,我们利用各节点状态的平均值为控制目标,设计了实现动力学网络同步的自适应控制方法[17,18].在本文中,我们将利用网络的一个节点状态作为控制的目标轨道,设计实现网络同步的自适应控制方法,这一改进可以降低控制系统的维数,使控制器结构更加简单,并可以减少控制过程中网络各节点间的信息传递量.
1 自适应控制方案
考虑由m个耦合节点构成的有一般耦合函数的动力学网络:

其中xi=(,…)T∈Rn是描述网络中第i个节点的状态向量,f(x)=(f1,f2,…,fn)T是描述孤立节点动力学行为的非线性向量函数,gi(x1,x2,…,xm):Rm×n→Rn(i=1,2,…,m)是未知的非线性耦合函数.
本文的目的是设计实现网络中各节点同步的有效控制方法,在每个节点上增加一个控制器ui=(,…,)T后,得到受控的动力学网络为:
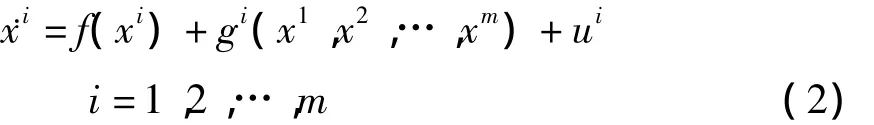
与文献[17,18]中的控制方法相比较,本文利用第l个节点的状态X(t)=xl作为控制的目标轨道.引入向量:
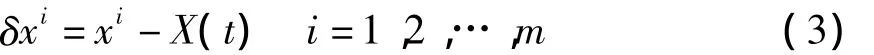
其中向量 δxi=(,…)T∈Rn经常被称为同步误差向量,它描述了网络中第i个节点偏离目标轨道X(t)的程度.
显然,误差向量δxi应该满足如下方程:
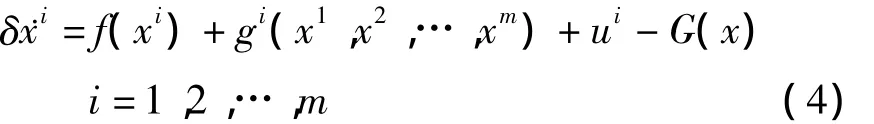
其中G(x)为向量函数:

通过引入误差向量 δxi(i=1,2,…,m),动力学网络(2)的同步问题被转化为误差系统(4)的稳定问题.因此我们的目的就是设计有效的控制器ui(i=1,2,…,m)使误差系统在原点渐进稳定.基于文献[3,17]中的工作,我们引入如下的自适应反馈控制器ui:
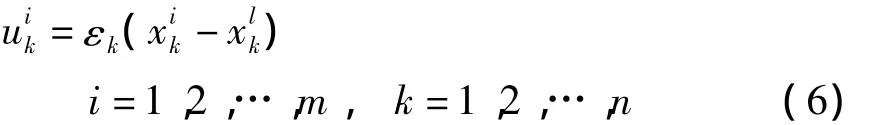
其中 ε =(ε1,ε2,…,εn)T∈Rn是自适应变化的反馈强度.反馈强度ε将按照如下法则自动更新:
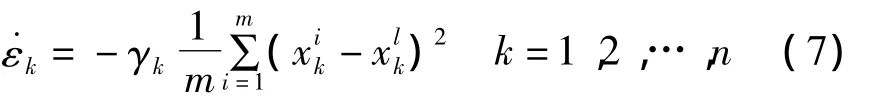
这里 γk(k=1,2,…,n)是任意正常数.
为获得所设计控制器有效的充分条件,在本文中将对非线性向量函数f(x)和耦合函数gi(x1,x2,…,xm)(i=1,2,…,m)作如下假设:
假设1 假设动力学网络(2)有界,且对任意xi(i=1,2,…,m)∈Ω 和yi(i=1,2,…,m)∈Ω(其中 Ω为有界集),存在正常数l1,l2满足如下不等式
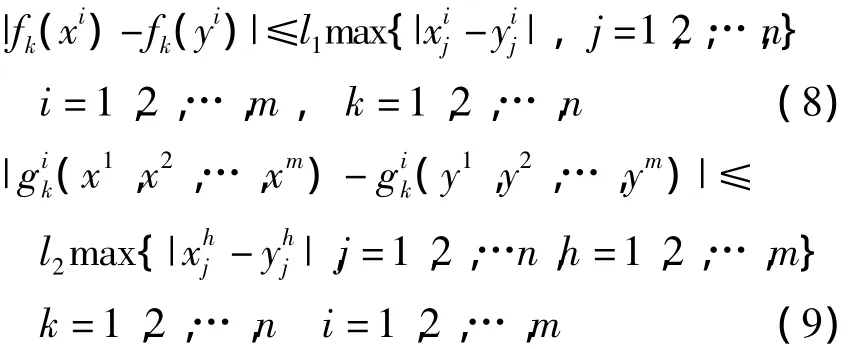
假设2 对任意x1=x2=…=xm,耦合函数gi(x1,x2,…,xm)满足:
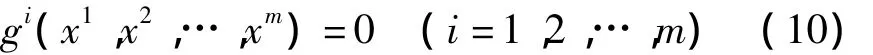
条件(8)和(9)通常称为Lipschitz条件,是一个比较普通的条件.条件(10)是为了确保动力学网络(2)的同步流形的存在.
为了证明在假设1和假设2下,受控动力学网络 (2)在控制器(6),(7)的作用下,各节点间能够达到同步,针对由(2),(6)和(7)构成的复合系统,我们引入如下是非负函数:
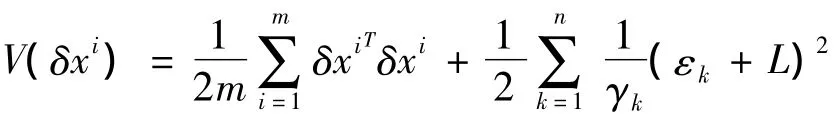
其中L为足够大常数.将函数V沿着复合系统的一条轨道求导得:
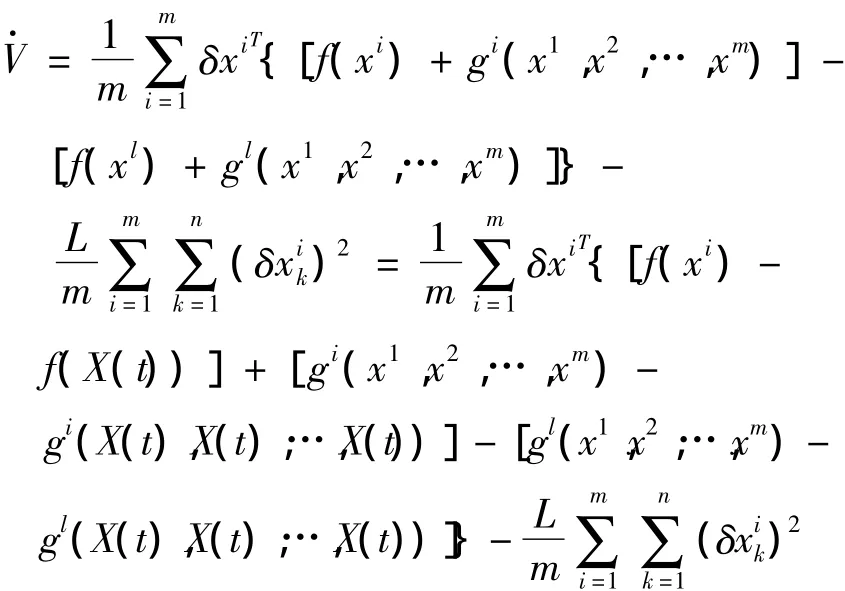
显然在上式中利用了条件(10),再利用不等式(8)和(9),容易证明

利用上述两个不等式有
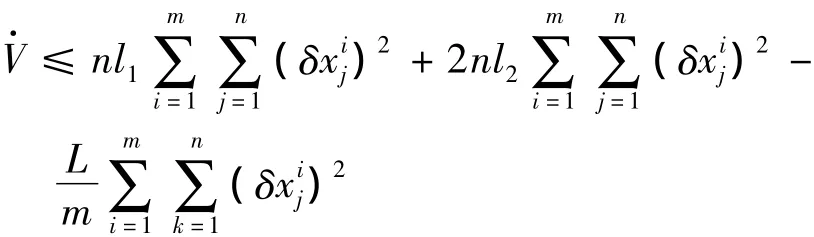
上式表明,如果选取L足够大,那么≤0,并且=0当且仅当=0,也就是集合
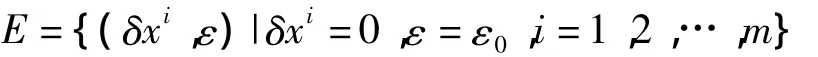
是=0中的最大不变集.根据LaSalle不变原理,以任何初值出发的复合系统的解都将渐进地收敛到集合E,即当t→∞时,则同步误差δxi→0和反馈强度 ε→ε0.
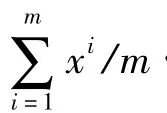
注2 在上述证明中,我们假设动力学网络(2)是有界的.实际上,当函数f(x)和gi(x)为非线性函数时,要证明网路系统 (2)的有界性是非常困难的,然而我们可以通过引入适当的分段和开关耦合数值策略来确保控制过程中系统 (2)的有界性[19].通过数值模拟,我们发现在很多情况下是不需要引入上述策略的,例如,节点系统拥有一个全局吸引混沌吸引子.
2 数值模拟
本节中,我们将通过数值模拟来验证所设计控制方法的有效性.我们利用统一混沌系统作为节点系统来描述节点的动力学行为.统一混沌系统可描述如下:
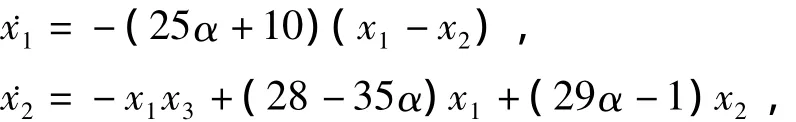

其中α为位于[0,1]间的正参数,根据文献[20],当0≤α<0.8时,系统 (11)属于广义 Lorenz系统;当 α=0.8时,系统 (11)属于Lü系统;当0.8<α≤1时,系统(11)属于广义Chen系统.
在数值模拟中,令网络的节点数m=100,并取耦合函数
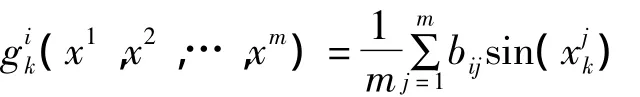
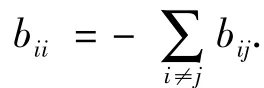
为了展示数值模拟结果,定义如下的量:
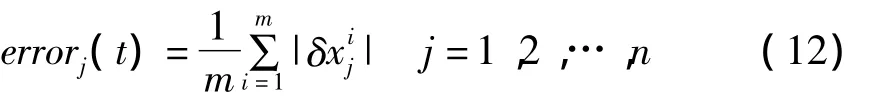
显然,当t→∞时,若errorj(t)→0,则所有状态→0(i=1,2,…,m,k=1,2,…,n).

图1 当α=0.2时,errori的时间历程图Fig.1 The temporal evolution of erroriwith α =0.2
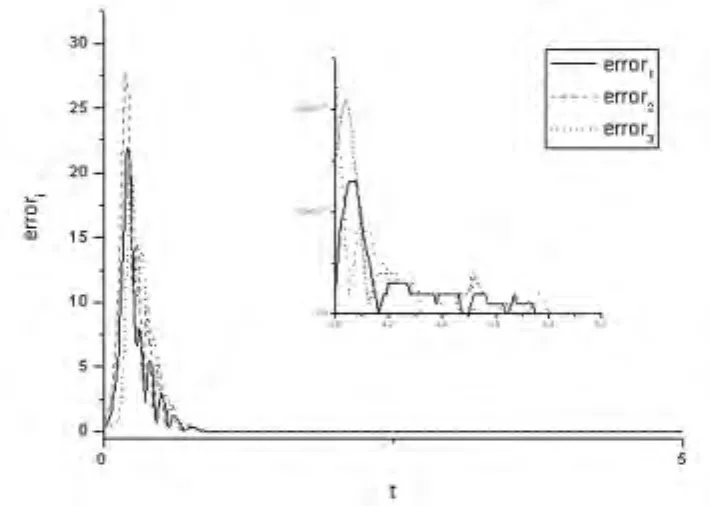
图2 当α=0.8时,errrori的时间历程图Fig.2 The temporal evolution of erroriwith α =0.8
在数值模拟中,利用四阶Runge-Kutta方法求解方程.系统初值(i=1,2,…,m,k=1,2,…,n)从[-1,1]间随机选取,并令控制强度ε初值为零,控制器中的常数 γk=0.1(k=1,2,…,n).图 1-图3中展示了数值模拟结果,在这些图中分别取参数 α =0.2(图1),α =0.8(图2),α =0.9(图3).通过这些图,容易看出我们的方法在很短的时间内就实现了网络个节点间的同步,并且同步的效果非常好.

图3 当α=0.9时,errori的时间历程图Fig.3 The temporal evolution of erroriwith α =0.9
3 结论
基于微分方程不变原理,本文设计了实现动力学网络同步的自适应控制方法.该控制方法非常有效,可以在事先不知道网络结构和节点系统结构的情况下,控制器根据同步误差自适应的调节控制强度,最终实现网络各节点间的同步,因此该方法有一定的通用性.与作者之前工作[17,18]中方法相比较,该方法对网络中所有节点施加相同的控制强度,因此对于整个网络只需额外的增加一个n维系统来计算控制强度,这可以降低系统的维数,简化控制器结构;利用一个节点的状态作为控制目标轨道,因此在控制过程中只需要将作为控制目标轨道的节点的状态传输给网络中的其它节点,这可以减少在控制过程中各节点间的信息传递量.利用该方法实现网络的同步,选取任何一个网络节点作为控制目标轨道都可以实现网络节点间的同步,至于如何选择哪个轨道作为控制目标使同步的时间最短是我们进一步的研究内容.该方法既简单又有效,将来会有一定的应用价值.
1 Pecora L M and Carroll T L.Synchronization in chaotic systems.Physical Review Letter,1990,64:821~824
2 Huang L L,Feng R P and Wang M.Synchronization of chaotic systems via nonlinear control.Physics Letter A,2004,320:271~275
3 Huang D B.Simple adaptive-feedback controller for identical chaos synchronization.Physical Review E,2005,71:037203
4 Tang F and Wang L.An adaptive active control for the modified Chua’s circuit.Physics Letters A,2005,346:342~346
5 Watts D J,Strogatz S H.Collective dynamics of smallworld'networks.Nature,1998,393:440 ~442
6 Pecora L M,Carroll T L.Master stability functions for synchronized coupled systems.Physical Review Letter,1998,80:2109~2112
7 Belykh V N,Belykh I V,Hasler M.Connection graph stability method for synchronized chaotic systems.Physica D,2004,195:159 ~187
8 Lu W L,Chen T P.New approach to synchronization analysis of linearly coupled ordinary differential systems.Physica D,2006,213:214~230
9 Pecora L M,Carroll T L,Johnson G,Mar D,Fink K S.Synchronization stability in coupled oscillator arrays:solution for arbitrary configuration.International Journal of Bifurcation and Chaos,2000,10:273 ~290
10 Wang X F,Chen G R.Synchronization in scale-free dynamical networks:robustness and fragility .IEEE Transactions on Circuits and Systems I,2002,49:54~62
11 Li X,Wang X F,Cheng G R.Pinning a complex dynamical network to its equilibrium.IEEE Transactions on Circuit and Systems I,2004,51:2074 ~2087
12 Song Q,Cao J D.On pinning synchronization of directed and undirected complex dynamical networks .IEEE Transaction on Circuits and Systems I,2010,57:672~680
13 张刚,张伟.复杂网络的脉冲同步.动力学与控制学报,2009,7:1 ~4(Zhang G,Zhang W.Impulsive synchronization of complex network.Journal of Dynamics and Control,2009,7:1~4(in Chinese))
14 Liu B,Liu X Z,Chen G R,Wang H Y.Robust impulsive synchronization of uncertain dynamical networks.IEEE Transactions on Circuits and Systems I,2005,52:1431~1441
15 Zhou J,Lu J A,Lü J H.Adaptive synchronization of an uncertain complex dynamical network.IEEE Transaction on Automatic Control,2006,51:652 ~656
16 Li Z,Jiao C,Lee J J.Robust adaptive global synchronization of complex dynamical networks by adjusting time-varying coupling strength.Physica A,2008,387:1369 ~1380
17 Xiao Y Z,Xu W,et al.Complete synchronization of un-certain chaotic dynamical network via a simple adaptive control.Chinese Physics B,2008,17:80~86
18 Xiao Y Z,Xu W,et al.Adaptive complete synchronization of chaotic dynamical network with unknown and mismatched parameters.Chaos,2007,17:033118
19 Lin W,Ma H F,Feng J F,Chen G R.Locating unstable periodic orbits:When adaptation integrates into delayed feedback control.Physical Review E,2010,82:046214
20 Lü J H,Chen G R,Cheng D Z,Celikovsky S.Bridge the gap between the Lorenz system and the Chen system.International Journal of Bifurcation and Chaos,2002,12:2917~2926
*The project supported by the National Natural Science Foundation of China(11202035,11201038,61202437),the Special Foundation for Basic Scientific Research of Central Colleges(CHD2011JC006 and 2013G2121017),and Foundation for Basic Scientific Research of Chang’an University
† Corresponding author E-mail:yuzhuxiao@chd.edu.cn
ADAPTIVE SYNCHRONIZATION OF DYNAMICAL NETWORKS USING STATE OF ONE NODE AS TARGET ORBIT*
Xiao Yuzhu1†Tang Sufang2
(1.Department of Mathematics and Information Science,Chang’an University,Xi’an710086,China)(2.School of Statistics,Xi’an University of Finance and Economics,Xi’an710100,China)
Based on the invariance principle of differential equation,a simple adaptive control method was proposed to synchronize the dynamical networks with the general coupling functions.Compared with other previous adaptive control methods,only one node’s states were used as target orbit to design the controller.This improvement can reduce the dimension of the system and amount of information transmitted among the nodes.To show the effectiveness of the proposed method,some numerical simulations were performed.
adaptive control, dynamical network, complex network, chaotic system, synchronization
8 July 2013,
19 July 2013.
10.6052/1672-6553-2013-108
2013-07-08 收到第 1 稿,2013-07-19 收到修改稿.
*国家自然科学青年基金(11202035,11201038,61202437),及中央高校基本科研业务费专项资金和长安大学基础研究自持计划专项资金(CHD2011JC006,2013G2121017)资助
E-mail:yuzhuxiao@chd.edu.cn

