大展弦比机翼非线性颤振剪裁设计新方法*

任智毅 金海波 丁 运亮

(南京航空航天大学航空宇航学院，南京 2 10016)

大展弦比机翼非线性颤振剪裁设计新方法*

任智毅†金海波 丁 运亮

(南京航空航天大学航空宇航学院，南京 2 10016)

针对大展弦比机翼水平弯曲模态参与耦合颤振问题，首先用考虑几何非线性的颤振分析方法研究了某大展弦比机翼的颤振特性，结果表明水平一弯模态参与耦合降低了机翼传统模式的线性颤振速度;然后研究了复合材料的铺层主刚度方向角对机翼非线性振动特性和颤振特性的影响规律，提出了大展弦比机翼非线性颤振剪裁设计的新方法．结果表明主刚度方向角的变化主要引起了水平一弯模态振型的改变，一般表现为主刚度方向角从机翼后梁向后缘偏转，该阶模态的相对扭转振型节线位置向前缘移动;反之，该节线位置后移．进一步非线性颤振分析，发现水平一弯模态振型的变化引起了该阶模态参与耦合颤振速度的明显改变，主要表现为该颤振型的颤振速度随该阶模态的相对扭转振型节线位置前移量的增加而增大．通过两个算例验证了结论的正确性．

大展弦比， 几何非线性， 颤振， 气动弹性剪裁， 节线

引言

高空长航时飞行器要求留空时间长、航程远，故大多采用高升阻比特性的大展弦比机翼布局形式．由于大展弦比机翼柔性大、变形大，因此具有非常显著的几何非线性特征，这改变了模态频率和振型，从而使得机翼颤振特性发生显著变化．对于实际机翼结构几何非线性颤振问题，由于结构变形复杂多样，如果直接采用CFD－CSD耦合方式［1－3］求解，其计算方法效率较低，在机翼初步设计阶段很难开展有效分析，因此目前主要通过在非线性平衡态附近应用动力学线性化方法［4］来预测大柔性机翼的颤振临界速度．谢长川、扬超等［5－6］采用该方法针对某大展弦比机翼结构进行研究，结果表明其水平一弯频率一般低于一阶扭转频率，在机翼承载变形时，几何非线性引起该两阶模态的运动耦合，这使得处在低阶的水平弯曲模态振型耦合有扭转分量，进而与临近的垂直弯曲模态相互耦合引起了非常严重的非线性气动弹性问题．但这些研究仅分析了水平弯曲模态参与耦合颤振的机理以及其对颤振特性的影响，并没有提出具体的防颤振设计方法，因此如何采用先进的气动弹性设计技术来解决大展弦比机翼非线性气动弹性问题，成为了一个非常具有研究价值的课题．

本文以某大展弦比复合材料机翼结构为对象，尝试在不改变机翼结构重量前提下，利用复合材料铺层方向的可设计性，从复合材料铺层角度入手，通过改变铺层角度的方式来研究其对几何非线性结构动力学特性以及非线性气动弹性特性的影响．

1 大展弦比机翼颤振分析

由于大展弦比机翼在飞行时，载荷作用下其翼尖变形较大，这使得常规固有振动分析所依赖的结构小变形假设不再适用，因此采用线性颤振分析方法可能得不到实际的颤振速度．由于大展弦比机翼在大变形后，材料仍满足线弹性本构关系，因此可通过在非线性平衡态附近构造机翼的线性动力学模型来计算结构在承载平衡态附近的动力学特性，然后基于平衡位置处的动力学特性建立频域气动弹性运动方程，并采用PK法求解该方程可得到机翼非线性变形后的颤振临界速度．本文以某大展弦比复合材料机翼为模型，该机翼采用的是单块式结构，其中翼肋采用的是垂直后梁的布局形式［7］．机翼有限元模型见图1，其展弦比约为25，机翼根部固支．

图1 机翼的有限元模型Fig．1 The finite element model of the wing

图2 颤振计算结果ig．2 The numerical result of the flutter analysis

图2给出了在等效海平面飞行速度50m/s～350m/s范围，采用线性和非线性颤振分析方法计算得出的颤振V－g曲线图，其中在非线性颤振分析中本文选用最大起飞状态为设计载荷情况．从图2可知，在线性分析情况下，随着速度的变化，水平一弯模态阻尼基本不变，而扭转模态阻尼发生很大变化，并在某个临界速度下，阻尼变为正值，对振动产生正激励，发生颤振，其颤振临界速度为276．05m/s．在非线性情况下，机翼的水平一弯模态阻尼随速度发生很大变化，并在较低速度下，阻尼变为正值，从而发生颤振，其颤振临界速度为153．85m/s，这远低于线性颤振计算结果．从以上分析可知考虑几何非线性影响后，水平一弯模态参与耦合的颤振型成为了决定机翼飞行安全的最低颤振形式，故有必要对该颤振型的防颤振设计方法进行深入研究．

2 主刚度角对机翼非线性振动特性的影响

在实际复合材料机翼结构设计中，由于受加工工艺的限制，铺层角度不能为任意值．根据复合材料层合板的一般铺层设计要求，尽量采用0°，±45°，90°的标准铺层角，这四个铺层角一般可以满足载荷设计要求，同时也能简化分析和制造，因此本文采用这四个标准铺层角度．由于气动弹性问题通常只考虑结构的总体刚度，复合材料铺层顺序对机翼结构的总体刚度影响不大，为了简化问题，本文把机翼结构的层合板的对称均衡铺层模型简化为［(±45°)n1，(90°)n2，(0°)n3］，其中 n1、n2、n3 表示层合板结构 ±45°、90°、0°的铺层厚度．

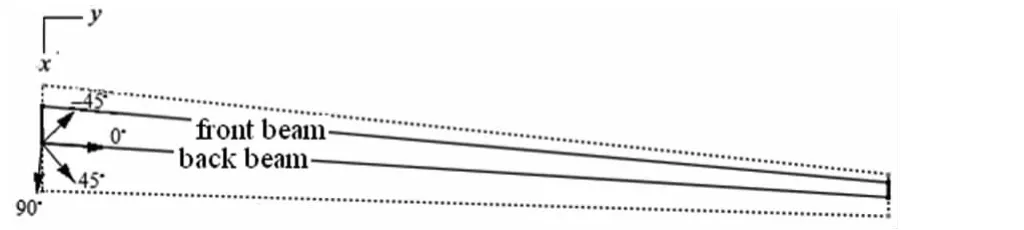
图3 机翼上、下蒙皮铺层角度的示意图Fig．3 The layer angle diagram of the wing up and down skin

上述处理就将一个复杂的铺层顺序模型用三个设计变量来表达，使得所研究问题得到了简化．根据单块式机翼结构的受力和传力特点，机翼主要是通过蒙皮传递机翼的弯矩和扭矩，因而影响机翼弯曲和扭转刚度的主要参数是机翼上、下蒙皮的铺层参数．由于大展弦比机翼的弯曲刚度较低，较小范围内增加复合材料的铺层数对结构的弯曲频率影响不大，而且增加铺层数不利于结构的轻量化设计，因此本文保持四个标准铺层角度的铺层厚度不变，即结构的质量特性不变，通过改变复合材料上、下蒙皮的铺层方向角来研究其对大展弦比机翼非线性颤振特性的影响规律．对于本文研究的复合材料机翼蒙皮，0°铺层方向角为蒙皮的主刚度方向，并假定0°方向角的初始方向沿机翼的后梁，各个铺层方向角示意图如图3所示．复合材料蒙皮铺层角度的设计方法是:以零铺层主方向角θ作为设计变量，其中零铺层主方向角相对于机翼后梁顺时针偏转时θ定为正值，±45°、90°方向角的变化方式分别为 ±45°+θ、90°+θ．

2．1 主刚度方向角对机翼非线性模态频率的影响

对于实际机翼结构几何非线性颤振问题，其颤振特性受到结构非线性振动特性的影响，因此本文首先分析复合材料蒙皮主刚度方向角对机翼振动特性的影响规律．假定本文研究的复合材料蒙皮主刚度方向角θ的变化范围是－5°～5°．在设计载荷作用下采用非线性模态求解方法得到不同θ情况下机翼的振动特性，其主要模态频率计算结果见表1．从表1中可知，主刚度方向角θ的变化对静平衡条件下机翼振动频率的影响较小．

表1 不同θ时，机翼非线性模态频率计算结果Table 1 The nonlinear modal frequency numerical results of the wing at the different θ

2．2 主刚度方向角对模态振型节线位置的影响

由于结构模态振型涉及复杂的几何形式表达，工程上一般不直接对结构振动的模态振型进行设计，而是抓住模态振动的关键信息－节线．传统的节线概念反映的是模态振型中不动点的连线［8］，大展弦比机翼在大变形条件下，其水平弯曲模态是和扭转模态相互耦合的，这种耦合导致很难采用传统概念定义本文应用的节线概念．因此本文在原有节线概念定义的基础上，提出了一种相对扭转振型节线的概念，处于该位置上的点，仅仅是在相对扭转振型中处于不动位置点的连线．具体的计算方法采用的是双向单侧搜索法［9］来搜索模态振型上垂向振幅为零的节点，进而将搜索到的节点连线作为节线．不同主刚度方向角θ下，机翼水平一弯和一阶扭转模态的相对扭转节线位置如图4～图6．

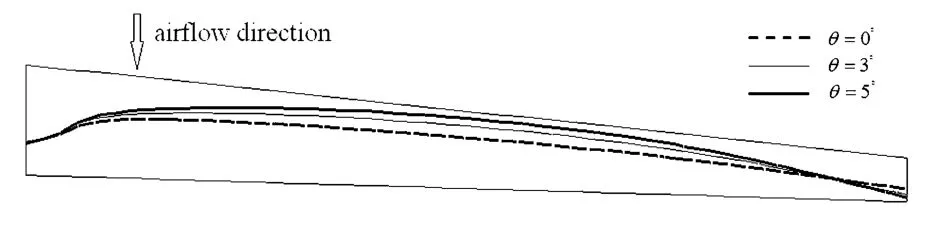
图 4 θ=0°，3°，5°时，水平一弯模态的节线位置ig．4 The section line of the first horizontal bending mode at the different θ

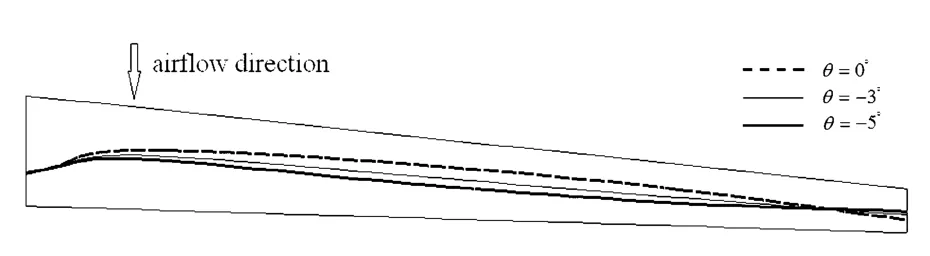
图5 θ=0°，－3°，－5°时，水平一弯模态的节线位置ig．5 The section line of the first horizontal bending mode at the different θ

从图4～图6可知，对于水平一弯模态振型，主刚度方向角θ为正时，这会使得水平一弯模态的相对扭转节线位置有较为明显的前移(向前缘方向移动)，且随着+θ的增加，该节线位置前移量增大;当θ为负值时，其结果与此相反．而对于一阶扭转模态振型，主刚度方向角的变化对该阶模态的相对扭转节线位置影响较小．

图6 不同θ时，一阶扭转模态的节线位置Fig．6 The section line of the first torsion mode at the different θ

2．3 改变节线位置的影响因素

为了分析节线位置变化的影响因素，以M．J．Patil和 D．H．Hodges［10］研究的 HALE 梁式机翼标准模型来说明影响节线位置改变的主要因素，其有限元模型见图7．首先为了保证HALE机翼模型和本文研究的机翼模型具有一定的相似性，本文要求这里采用的HALE模型要和所研究的机翼模型具有相近弯曲变形和振动频率．相应的展向和弦向弯曲刚度以及扭转刚度分别为9×105N·m2、7×106N·m2、5．5 ×105N·m2，其它结构数据参见文献［12］．外载为在机翼上施加单位展向气动力300 N/m．

图7 HALE机翼有限元模型Fig．7 The finite element model of the HALE wing

为了分析相对扭转振型节线位置的改变规律，本文从如下两种情况进行讨论:(1)机翼质量特性和刚度性不变，调整HALE机翼的扭转变形，即在机翼上加载不同的单位展向扭矩．(2)机翼刚度特性和外载不变，改变HALE机翼的质量分布，即通过如下两种方式进行对比研究:①把HALE梁式机翼前缘位置的结构配重提高0．5倍;②把HALE梁式机翼后缘位置的结构配重提高0．5倍．

对于情况一，其主要模态频率计算结果见表2，其中使机翼抬头的扭矩定义为正;机翼水平一弯和一阶扭转模态的相对扭转节线位置见图8．从表2中可知，扭矩对静平衡条件下机翼振动频率的影响较小．从图8中可知，扭矩对机翼水平一弯模态的相对扭转振型节线位置影响较大，而对一阶扭转模态的相对扭转节线位置影响较小．其主要表现为:正扭矩使得机翼水平一弯模态的相对扭转振型节线位置前移，且随着正扭矩的增加，该节线位置前移量加大;反之，负扭矩的增加使得该节线位置后移量加大．对于情况二，其主要模态频率计算结果见表3，水平一弯和一阶扭转模态的相对扭转振型节线位置如图9所示．从表3中可知，两种质量分布下，机翼的振动频率相等．从图9中可知，前缘加配重使得机翼的水平一弯和一阶扭转模态的相对扭转振型节线位置均发生了变化．其主要表现为:前缘加配重，机翼重心前移，该两阶模态的相对扭转振型节线位置前移;后缘加配重与此相反．对于2．2节中的复合材料机翼，由于主刚度方向角的变化没有改变机翼的质量分布，通过上述分析，可以得知，该机翼的水平一弯模态的相对扭转振型节线位置的前移主要是由于主刚度方向角从机翼后梁向后缘偏转，导致机翼产生附加的正扭矩，该扭矩使得机翼的相对扭转振型节线位置前移;反之，该节线位置后移．前面分析表明，蒙皮主刚度方向角的变化对机翼模态频率影响较小，而对水平弯曲模态振型影响较大．由于水平弯曲模态振型的变化就有可能引起其参与耦合颤振特性的改变．因此，下面进一步研究复合材料蒙皮主刚度方向角变化对机翼非线性颤振特性的影响．

表2 不同扭矩时，机翼非线性模态频率计算结果Table 2 The nonlinear modal frequency numerical results of the wing at the different torques

表3 两种质量分布下，机翼非线性模态频率计算结果Table 3 The nonlinear modal frequency numerical results of the wing at two mass distributions

图8 不同扭矩时，水平一弯(左)和一阶扭转(右)的振型节线位置Fig．8 The section line of the first horizontal bending(left)and torsion(right)mode at the different torques

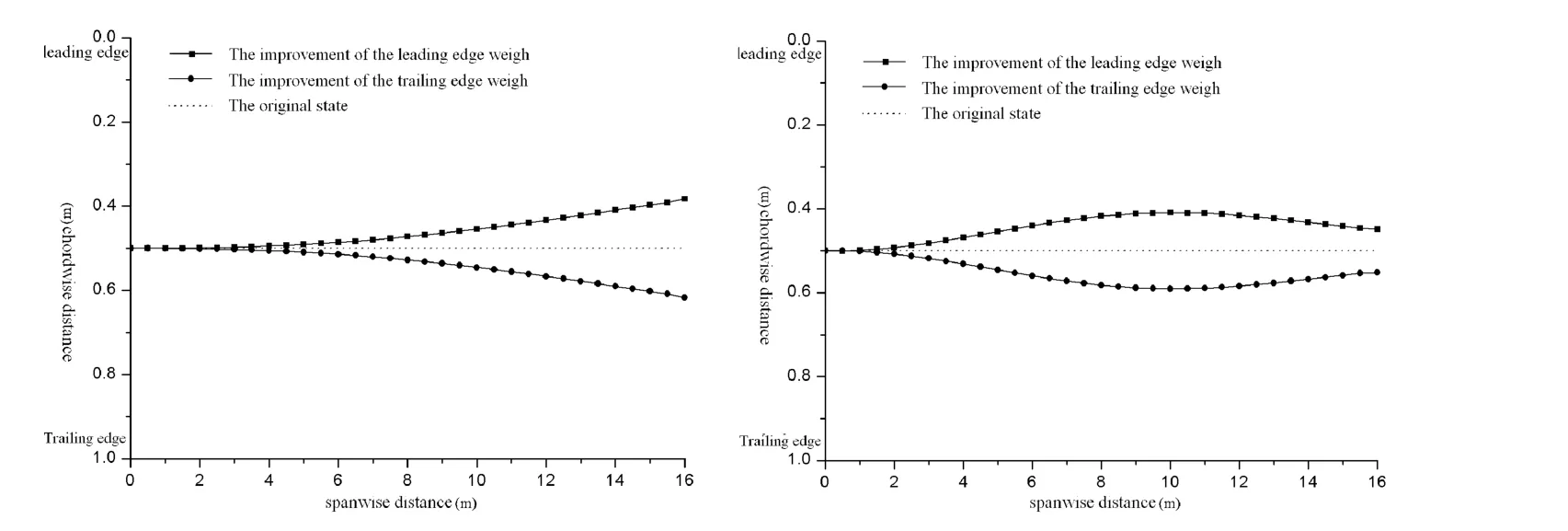
图9 两种质量分布下，水平一弯左)和一阶扭转(右)振型节线位置ig．9 The section line of the first horizontal bending(left)and torsion(right)mode at two mass distributions

3 主刚度角对机翼非线性颤振特性的影响

3．1 主刚度方向角对机翼颤振速度的影响

由初步非线性颤振分析图2可知，机翼出现了两个颤振分支，第一分支为水平一弯模态参与耦合颤振型;第二分支为一阶扭转模态参与耦合颤振型．本文进一步评估机翼不同主刚度方向角对该两种颤振型的颤振速度的影响，其计算结果见表4，表中N表示在所选海平面飞行速度范围内没发生颤振．

从表4中可知，当θ为正时，能够较为明显地提高水平弯曲模态参与耦合颤振型的颤振临界速度，且随着+θ的增加，该颤振型的颤振临界速度逐渐增大;反之，－θ会减小该颤振型的颤振临界速度．由于主刚度方向角的变化对机翼非线性振动频率影响较小，而对机翼水平一弯模态振型影响显著，因此水平一弯模态参与耦合颤振型的颤振临界速度的变化是由该阶模态振型的改变引起的．当θ为正时，由2．2节内容分析表明，该阶模态振型的相对扭转振型节线位置向前缘方向移动，进一步非线性颤振特性研究表明，该颤振型的颤振临界速度提高，故本文认为节线前移能够提高机翼颤振临界速度;节线后移与此相反．对于第二支颤振模态，由于主刚度方向角的变化对一阶扭转模态频率和模态振型节线位置影响较小，因此其对该颤振型的颤振临界速度影响不明显．

表4 不同θ时，机翼非线性颤振计算结果Table 4 The nonlinear flutter numerical results of the wing at the different θ

3．2 结论验证

为了进一步说明相对扭转振型节线位置前移能够提高机翼颤振速度，本文进一步对2．3节中两种情况下HALE机翼模型的非线性颤振临界速度进行评估，情况一和情况二的计算结果分别见表5和表6．从颤振计算结果上看，正扭矩和重心前移均引起水平一弯模态的相对扭转振型节线位置前移，其参与耦合的颤振速度均得到提高，这进一步说明相对扭转振型节线位置的前移能够提高颤振速度．

4 结论

在大展弦比机翼非线性颤振剪裁设计时，通过控制复材蒙皮主刚度方向角，使得诱发机翼颤振的扭转型模态的振型节线位置向前缘移动，能够在不增加结构重量的前提下提高机翼的非线性颤振临界速度．

表5 不同扭转时，HALE梁式机翼非线性颤振计算结果Table 5 The nonlinear flutter numerical results of the wing at the different torques

表6 两种质量分布下，HALE梁式机翼非线性颤振计算结果Table 6 The nonlinear flutter numerical results of the wing at two mass distributions

1 Dunn P，Dugundji J．Nonlinear stall flutter and divergence analysis of cantilevered graphite/epoxy wings．AIAA Journal，1991，30(1):153 ～162

2 Liu J K，Zhao L C．Bifurcation analysis of airfoil in incompressible flow．Journal of Sound and Vibration，1992，154(1):117～124

3 赵永辉，胡海岩，具有操纵面间隙非线性二维翼段的气动弹性分析．航空学报，2003，21(6):521～525(Zhao Y H，Hu H Y．Aeroelastic analysis of a two－dimensional airfoil with control surface freeplay nonlinearity．Acta Aeronautica et Astronautica Sinica，2003，21(6):521～525(in chinese))

4 Tang D，Dowell E H．Experimental and theoretical study on aeroelastic response of hight－aspect－ratio wings．AIAA Journal，2001，39(8):1430 ～1441

5 Xie C C，Yang C．Linearization method of nonlinear aeroelastic stability for complete aircraft with high－aspect－ratio wings．Science China Techological Sciences，2001，54:403～411

6 谢长川，杨超．大展弦比飞机几何非线性气动弹性稳定性的线性化方法．中国科学:技术科学，2011，41(3):385～393(Xie C C，Yang C．Linearization method of nonlinear aeroelastic stability for complete aircraft with high－aspect－ratio wings．Science China Techological Sciences，2011，41(3):385～393(in chinese))

7 Niu M C Y．Airframe structural design．Hong Kong:Conmilit Press，1998

8 胡海岩，孙久厚，陈怀海．机械振动与冲击．北京:航空工业出版社，2002:63～66(Hu H Y，Sun J H，Chen H H．Mechanical Vibration and Shock．Beijing:Aviation Industry Press，2002:63～66(in chinese))

9 陈怀海，周传荣．一种满足多阶固有频率和节线位置等要求的结构动力学设计方法．应用力学学报，1996，13(1):59～64(Chen H H，Zhou C R．Structural design subjected to multiple frequencies positions of nodal lines and other constraints．Chinese Journal of Applied Mechanics，1996，13(1):59～64(in chinese))

10 Patil M J，Hodges D H．On the importance of aerodynamic and structural geometrical nonlinearities in aeroelastic behavior of high－aspect－ratio wings．Journal of Fluids and Structures，2004，905～915

*The project supported by the National Natural Science Foundation of China(10872091)and the Special Science Foundation of Nanjing University of Aeronautics＆Astronautics(NS2011003)

† Corresponding author E－mail:renzhiyi335@sina．com

A NEW METHOD ON FLUTTER TAILORING TECHNIQUES OF HIGH-ASPECT-RATIO WINGS*

Ren Zhiyi†Jin Haibo Ding Yuliang
(College of Aerospace Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing210016，China)

A method was presented to analyze the nonlinear flutter．Based on this method，the flutter characteristics of the high aspect wing were illustrated．The numerical results show that the flutter speed is decreased when the first horizontal bending mode involved．Secondly，this study discussed how the main direction of the composite influenced the character of the nonlinear vibration and flutter，and established the method of the flutter clipping to the high aspect wing．And the result shows that the stiffness of structure can be changed by changing the main direction of the composite．It mainly changes the horizontal bending mode，makes the main direction tend to the trailing edge，and then makes the section line move to the leading edge．Further analyzing the nonlinear flutter reveals that it is the changing of the horizontal bending mode that causes the flutter speed change obviously．And by the section line of this mode moves ahead，the flutter speed will become larger．In the study，two examples were illustrated to validate its truthiness．

high－aspect－ratio， geometry nonlinear， flutter， aeroelastic tailoring， section line

12 June 2014，

23 July 2014．

10．6052/1672－6553－2014－061

2014－06－12 收到第 1 稿，2014－07－23 收到修改稿．

*国家自然科学基金资助项目(10872091)，南京航空航天大学基本科研业务费专项科研项目(NS2011003)

E－mail:renzhiyi335@sina．com