火箭结构系统纵向模态自动辨识方法*

方勃 唐冶 杨飞虎 张业伟 臧健

(1．哈尔滨工业大学航天学院，哈尔滨 1 50001)(2．沈阳航空航天大学航空航天工程学部，沈阳 1 10136)(3．北京环境强度研究所，北京 1 00076)(4．上海大学上海市应用数学和力学研究所，上海 2 00072)

火箭结构系统纵向模态自动辨识方法*

方勃1，2唐冶1†杨飞虎3张业伟4臧健2

(1．哈尔滨工业大学航天学院，哈尔滨 1 50001)(2．沈阳航空航天大学航空航天工程学部，沈阳 1 10136)(3．北京环境强度研究所，北京 1 00076)(4．上海大学上海市应用数学和力学研究所，上海 2 00072)

针对工程中需要从火箭结构系统的整体模态中识别纵向模态，根据模态有效质量理论，提出了一种识别火箭结构系统纵向模态的自动辨识方法．以具有集中质量系统的振动特性作为算例，通过有限元软件，建立了具有集中质量系统的梁模型，利用自动辨识的方法，自动辨识出系统的纵向模态，并与应用模态分析法所计算的系统模态信息相比较，这种自动辨识方法不仅能准确的辨识出振动系统的纵向模态，而且还具有自动高效的识别特点．为准确快速建立液体火箭POGO振动系统的动力学模型等工程系统的模型提供理论依据．

火箭结构系统， 纵向模态， 模态有效质量， 自动辨识， 模态分析

引言

液体火箭POGO振动的现象是指液体火箭推进系统的流体脉动和箭体结构系统的纵向振动发生耦合而产生的自激振动，这种振动现象会给火箭飞行带来很多不利的影响［1－7］．从箭体结构整体模态中挑出纵向模态可准确把握火箭结构系统的纵向振动特性，这是分析和抑制POGO振动的前提和基础．对于火箭结构系统的模态信息，学者们主要采用了有限元和试验的方法通过计算而得到．Pan等［8］采用耦合质量方法模拟了液体推进剂，实现了基于梁模型的火箭结构系统的建模和动力学特性分析．吴素春等［9］研究了载人运载火箭全箭模态试验技术，取得了载人运载火箭各特征秒状态下的频率、振型、阻尼和振型斜率等全部模态数据，通过理论分析可知试验取得的全部模态数据可靠，为稳定系统设计及火箭飞行过程中宇航员的振动环境提供了试验依据．王建民等［10］采用试验与有限元分析相结合的技术途径，对捆绑火箭模态结果进行了分析，并给出了捆绑火箭的模态族和纵横扭耦合模态特征．

结构系统的模态有效质量能够反映出结构的很多动力特征，它代表在基础激励下，各阶次模态的动力学质量和模态参与因子的大小，很多学者采用了这种理论解决了许多工程实际的问题．文献［11］中的Clough首次提出结构振动系统的模态有效质量的概念用于研究结构的动力学相关问题．Liu等［12］基于模态有效质量理论建立了安装有效载荷的整星隔振系统的简单模型，并分析了阻尼和刚度参数对此隔振系统的影响．文献［13］阐述了结构在基础激励下，系统有效模态质量与有限元模型的准确性之间是一种直接的关系．文献［14］介绍了大型复杂结构在基础激励下有效模态质量的估算方法．石进峰等［15］介绍了一种简单的基于有效模态质量与结构质量的比值来判断有限元模态精确度的方法，并结合多自由度系统的振动特性验证了此方法的正确性．刘辉等［16］针对弯扭耦合振动力学模型的特点，利用有限元和数学模型相结合，建立了车辆动力传动系统弯扭耦合振动模型，探讨耦合模态中的振动形式以及模态参与因子和有效质量，研究齿轮时变啮合刚度和啮合阻尼对多轴齿轮动力传动系统弯扭耦合振动模态的影响情况，然后对齿轮传动系统进行弯扭耦合振动台架试验，将试验数据与仿真计算结果进行对比，从而验证了有限元模型的正确性．

本文针对在液体火箭POGO振动分析中需要建立箭体结构系统的纵向振动模型，根据模态有效质量理论，提出了一种自动识别火箭结构系统纵向模态的方法．以具有集中质量系统的振动特性作为算例，通过有限元软件，建立了具有集中质量系统的梁模型，利用自动辨识的方法，自动辨识出系统的纵向模态，并与应用模态分析法所计算的系统模态信息相比较，来说明自动辨识方法的有效性和优点．为进一步分析火箭POGO振动特性，快速的设计火箭结构参数提供有力工具．

1 火箭结构系统的模态有效质量理论

描述液体火箭结构系统的动力学模型为

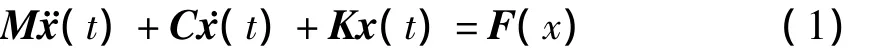
式中，M、C和K分别为火箭结构系统的质量矩阵、阻尼矩阵和刚度矩阵．t为时间，F(t)为系统受到的外力列阵．x(t)(t)和(t)分别为系统的状态位移列阵、状态速度列阵和状态加速度列阵．

设方程(1)的解为

式中，φi为火箭结构系统的第i阶特征向量，j表示虚数单位，即为火箭结构系统的第i阶固有频率．将方程(2)代入方程(1)中，可得火箭结构系统的特征方程为

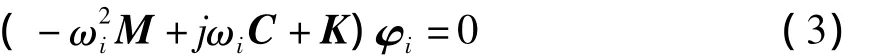
根据方程(3)，可计算出箭体结构系统的振动固有频率ωi和所对应的特征向量φi(i=1，2，…)．

定义火箭结构系统的系数矩阵为

式中，Φ为火箭结构系统模态矩阵，它是由系统的特征向量φi(i=1，2，…)所组成．r为影响矩阵，表示结构基础的单位静位移使各个质点所产生的位移．利用火箭结构系统的固有振型正交性，将质量矩阵M对角化，则第i对角元素为

根据方程(4)和方程(5)，可计算出箭体结构系统的第i阶模态在自由度g上的模态参与因子为

通过方程(4)、方程(5)和方程(6)，可导出箭体结构系统的第i阶模态在自由度g上的模态有效质量为

假设火箭结构系统为串连刚体系，所以根据式(7)，火箭结构系统的第i阶模态在f方向上的模态有效质量可近似表示为

式中，ml为火箭结构系统中第l个单元质量，N为单元总数表示箭体结构系统在第l个单元中第i阶模态在f方向上的振型．f方向分别为箭体结构系统沿横向(X)、法向(Y)、纵向(Z)平动以及绕横向转动(RX)、绕法向转动(RY)、绕纵向转动(RZ)．

2 识别火箭结构纵向模态的判据

根据液体火箭结构系统的实际情况以及箭体结构系统的模态有效质量理论，提出辨识箭体结构系统纵向模态的判据为:若火箭结构系统振动的模态在纵向Z方向的模态有效质量与其它方向的最大模态有效质量之比大于某一指定的数值，则该模态为箭体结构系统的与其它任意方向不发生耦合的纵向模态．

3 算例分析

将火箭纵向模态的自动辨识方法应用到具有集中质量系统的梁模型中，辨识出的梁模型的纵向模态和常规的模态分析法所辨识的结果进行比较，说明本文所提出的方法的有效性．

3．1 具有集中质量系统的梁模型

利用有限元软件，建立具有11个集中质量块结构系统的梁模型，长度为10m，每个集中质量重3700Kg，弹性模量为68GPa，泊松比为0．31，系统采用分支梁单元，具体如图1所示．

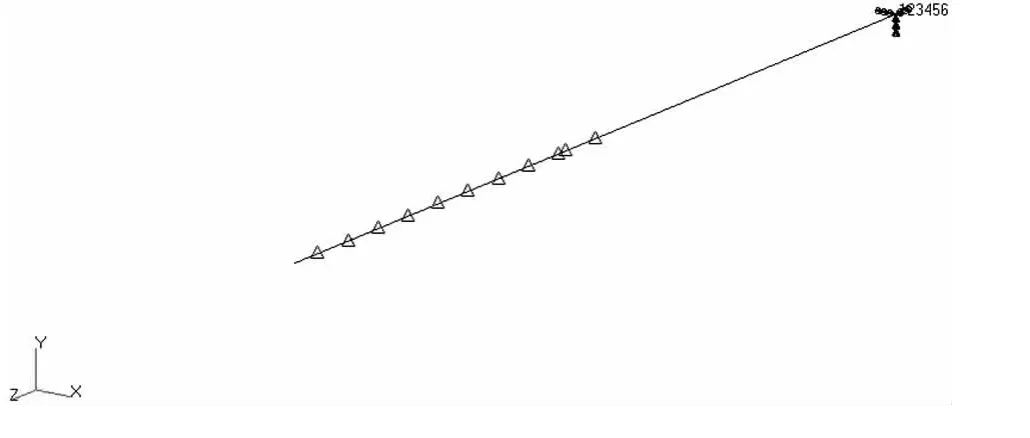
图1 具有集中质量系统的梁模型Fig．1 Beam model of the system with lumped mass

表1 具有集中质量系统的各质量块分布情况Table 1 Distributing case of each mass in lumped mass system

在图1所示的具有集中质量系统的梁模型中，系统整体共有六个运动方向，即系统沿横向(X)、法向(Y)、纵向(Z)平动以及绕横向转动(RX)、绕法向转动(RY)、绕纵向转动(RZ)．系统的各质量块单元序号从左到右依次为1～11，这11个质量块的分布情况具体如表1所示．

3．2 具有集中质量系统纵向模态的辨识

根据具有集中质量系统的实际情况，利用辨识火箭结构系统纵向模态的自动辨识方法，提出辨识具有集中质量系统纵向模态的判据为:若系统的模态在纵向(Z)方向的模态有效质量与其它方向的最大模态有效质量之比的数量级大于3，则该模态为系统的纵向模态．根据这个判据，可从系统的整体模态中辨识出纵向模态．

应用有限元技术，可提取具有集中质量系统的动力学特性数据，利用火箭结构系统模态有效质量的计算方法，可计算出具有集中质量系统的前20阶模态有效质量在各个方向上的分布，如表2所示．

表2 具有集中质量系统的模态有效质量分布情况Table 2 Distributing case of modal effective mass in lumped mass system

根据模态有效质量理论以及本文所提出的具有集中质量系统的纵向模态辨识的判据，利用MATLAB软件，可编制出识别系统纵向模态的界面，将表2中模态有效质量分布文件输入到界面中，可自动辨识出系统的纵向模态，如表3所示．

表3 具有集中质量系统纵向模态的辨识结果Table 3 Identificaiton result of longitudinal modes in lumped mass system

基于如图1所示的具有集中质量系统的梁模型，通过MSC/NASTRAN软件，利用模态分析法，可分析出此系统的模态信息，如表4所示．

从表4可以看出，具有集中质量系统的第8阶和第15阶模态为该系统的前两阶纵向模态．

比较表3和表4得，利用本文所提出的方法辨识出的具有集中质量系统的纵向模态，与应用模态分析法分析得到的该系统的纵向模态结果是一致的．常规的模态分析法辨识纵向模态是需要利用有限元软件分析，然后通过系统每一阶次具体的振动模态形式比较而得，而本文的方法通过识别纵向模态的判据编制界面，只要从有限元软件中计算出动力学特性数据，便可自动得到结果．这说明利用模态有效质量理论来辨识系统的纵向模态的方法不仅能准确的辨识出纵向模态，而且还具有自动高效的识别特点．另外，利用本文的方法，可编制出识别火箭结构系统在各个特征秒状态下纵向模态的界面，能自动的辨识出火箭全部状态的纵向模态．和传统的模态分析法相比较，识别的速度更快，效率更高．

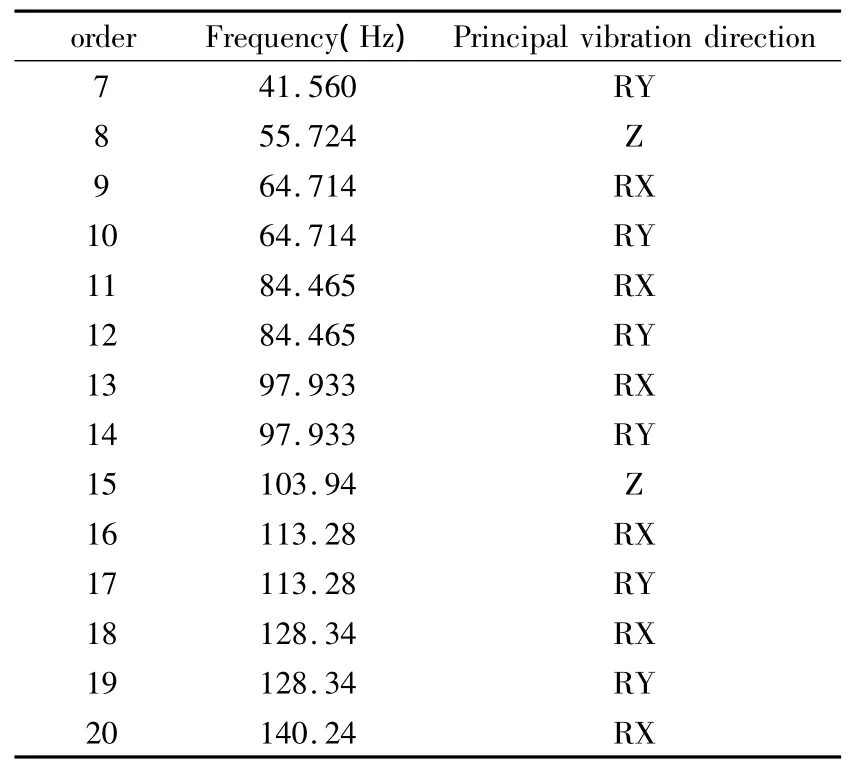
表4 具有集中质量系统的模态信息Table 4 Modal information in lumped mass system

4 小结

本文针对在火箭POGO振动分析中需要建立结构系统的纵向振动模型，根据模态有效质量理论，提出了一种自动识别结构系统纵向模态的方法．以辨识具有集中质量系统的纵向模态为例，通过比较利用本文提出的方法和模态分析法的辨识结果，表明利用模态有效质量理论来辨识系统的纵向模态的方法不仅能准确的辨识出系统的纵向模态，而且还具有自动高效的识别特点．为准确建立液体火箭POGO振动系统的动力学模型等工程系统的模型，快速分析工程系统的动力学特性提供有力工具．

1 Dotson K W，Rubin S，Sako B H．Mission－specific POGO stability analysis with correlated pump parameters．Journal of Propulsion and Power，2005，21(4):619 ～626

2 Zhao Z H，Ren G X，Yu Z W，et al．Parameter study on pogo stability of liquid rockets．Journal of Spacecraft and Rockets，2011，8(3):537～541

3 Rubin S．Longitudinal instability of liquid rockets due to propulsion feedback(POGO)．Journal of Spacecraft andRockets，1966，3(8):1188～1195

4 黄怀德．液体火箭的POGO振动研究．振动工程学报，1987，1(1):5 ～13(Huang H D．Research into POGO vibration of liquid rockets．Journal of Vibration Engineering，1987，1(1):5 ～13(in Chinese))

5 严海，方勃，黄文虎．液体火箭的POGO振动研究与参数分析．导弹与航天运载技术，2009，304(6):531～534(Yan H，Fang B，Huang W H．Research and parameter analysis of POGO vibration in liquid rocket．Missiles and Space Vehicles，2009，304(6):531～534(in Chinese))

6 王其政，高万镛，顾永春等．跷振(POGO)稳定性可靠性算法与参数分析．宇航学报，1986，(2):29～47(Wang Q Z，Gao W Y，Gu Y C，et al．POGO stability reliability and parameters analysis．Journal of Astronautics，1986，(2):29～47(in Chinese))

7 Dordain J J，Lourme D，Estoueig C．Study on POGO effect on launchers Europa－2 and Diamond－B．Acta Astronautica，1974，1(11):1357～1384

8 Pan Z W，Xing Y F，Zhu L W，et al．Liquid propellant analogy technique in dynamic modeling of launch vehicle．Science China:Technological Sciences，2010，53(8):2102～2110

9 吴素春，贾文成，邱吉宝．载人运载火箭全箭模态试验．宇航学报，2005，26(5):531～534(Wu S C，Jia W C，Qiu J B．Integrated modal test for the manned launch vehicle．Journal of Astronautics，2005，26(5):531 ～ 5 34(in Chinese))

10 王建民，荣克林，冯颖川等．捆绑火箭全箭动力学特性研究．宇航学报，2009，30(3):821～826(Wang J M，Rong K L，Feng Y C，et al．The research of dynamic characteristics for the strap－on launch vehicle．Journal of Astronautics，2009，30(3):821 ～826(in Chinese))

11 Clough R W，Penzien J．Dynamics of structures．New York:Mcgraw－Hill Incorporated，1975

12 Liu L K，Zheng G T．Parameter analysis of PAF for whole－spacecraft vibration isolation．Aerospace Science and Technology，2007，11(6):464～472

13 Appel S．Calculation of modal participation factors and effective mass with the large mass approach．Berlin，Heidelberg，GERMANY:Springer，1992:1654 ～1661

14 Ramin S，Yvan S，Nicolas E．Efficient estimation of effective mass for complex structures under base excitations．Canadian Aeronautics and Space Journal，2003，49(6):135～143

15 石进峰，吴清文，郭万纯等．基于有效模态质量的有限元建模．系统仿真学报，2013，25(5):995～998(Shi J F，Wu Q F，Guo W C，et al．Application of modal effective mass for finite element model construction．Journal of System Simulation，2013，25(5):995 ～998(in Chinese))

16 刘辉，项昌乐，孙恬恬等．车辆动力传动系统弯扭耦合振动模型的建立及复模态分析．机械工程学报，2010，46(24):67 ～74(Liu H，Xiang C L，Sun T T，et al．Construction of Bending－torsional coupled vibration model and complex modal analysis of the vehicle powertrain．Journal of Mechanical Engineering，2010，46(24):67 ～74(in Chinese ))

*The project supported by the National Natural Science Foundation of China(11202140)

† Corresponding author E－mail:tangye2010_hit@163．com

AN AUTOMATIC IDENTIFICATION METHOD FOR LONGITUDINAL MODES OF STRUCTURAL SYSTEM OF ROCKET*

Fang Bo1，2Tang Ye1†Yang Feihu3Zhang Yewei4Zang Jian2

(1．School of Astronautics，Harbin Institute of Technology，Harbin150001，China)(2．China Department of Astronautics，Shenyang Aerospace University，Shenyang110136，China)(3．Beijing Institute of Structure and Environment Engineering，Beijing100076，China)(4．Shanghai Institute of Applied Mathematics and Mechanics，Shanghai200072，China)

Aiming at the problem that the longitudinal modes of structural system of rocket need to be identified from its integral modes in engineering，a method that automatically identifies the longitudinal modes of structural system of rocket was proposed according to the theory of modal effective mass．Taking the vibration characteristics of system with lumped mass as a computing example，applying the finite element software，the beam model of system with lumped mass was established，and the longitudinal modes of the system were automatically identified based on the method．Compared with the system modal information calculated by the method of modal analysis，this automatic identification method not only can accurately identify the longitudinal modes of vibrating system，but also has automatic and high efficiency identification feature．It provides a theoretical basis for the dynamic model of POGO vibrating system in liquid rockets and other model of engineering systems to be accurately and promptly established．

structural system of rocket， longitudinal modes， modal effective mass， automatic identification，modal analysis

20 June 2014，

11 July 2014．

10．6052/1672－6553－2014－043

2014－06－20 收到第 1 稿，2014－07－11 收到修改稿．

*国家自然科学基金资助项目(11202140)

E－mail:tangye2010_hit@163．com