平板裂缝天线热加工误差数值仿真及其对天线电性能的影响*

肖志城，朱敏波，宋立伟，段宝岩

(西安电子科技大学电子装备结构设计教育部重点实验室， 陕西 西安 710071)

平板裂缝天线热加工误差数值仿真及其对天线电性能的影响*

肖志城，朱敏波，宋立伟，段宝岩

(西安电子科技大学电子装备结构设计教育部重点实验室， 陕西 西安 710071)

基于学科交叉，文中研究了热加工对平板裂缝天线电性能的影响问题。首先，应用热弹塑性理论和生死单元技术，模拟了降温曲线、焊料及工装方式3种不同因素对天线残余应力、变形的影响。然后，文中提出了结构位移场与电磁场的场耦合理论模型，研究了热加工误差对天线电性能(增益、副瓣电平等)的影响。最后，将理论与方法应用于某机载平板裂缝天线的实际工程中，取得了较为满意的结果。

平板裂缝天线；焊接变形；降温曲线；焊料；工装方式；电性能

引 言

随着电子技术、信息技术的快速发展以及军事需求的日益提高，对电子装备如平板裂缝天线的电性能要求越来越高，正朝着高频段、高增益，高密度、小型化，快响应、高指向精度的方向发展。作为一种典型的机电结合的复杂电子装备，平板裂缝天线由于具有体积小、重量轻、结构紧凑、口径利用率高、天线增益高、副瓣电平低等特点而得到了广泛应用。

平板裂缝天线由多层薄壁波导腔体构件(厚度大约0.5～1 mm)构成，即由激励波导、耦合波导与辐射波导组成。通过将这3个薄壁腔体件焊接(盐浴焊或真空钎焊)而成型。平板裂缝天线中作为微波传输通道的波导有严格的尺寸精度、位置精度以及形状精度要求。以工作在X频段的平板裂缝天线为例，要求波导误差不超过±0.05 mm[1]。值得指出的是，实际制造过程中，对波导加工精度的要求虽然很高，但通过高精度的加工中心加工，精度不难实现。遗憾的是，前面的高精度往往被后面的热加工焊接成型过程给吃掉了。也就是说，保证平板裂缝天线高加工精度的主要矛盾是后面的焊接成型过程，而不是前面的波导加工精度。因此，合理选择热加工工艺，以保证平板裂缝天线加工精度及其电性能要求，已成为一个关键技术问题。

从公开报道的文献看，大多数研究主要集中在工艺、焊接接头等单方面的研究上。也有学者对天线焊接时的工装受力和工艺进行了分析[2-4]，但对平板裂缝天线焊接的热变形和残余应力分布及其对电性能影响的研究却鲜见报道。为此，本文针对大型机载平板裂缝天线的热加工过程进行数值模拟，较系统地研究不同的降温曲线、焊料及工装方式对天线结构最终的焊接变形和残余应力的影响情况，以及焊接变形对天线电性能的影响。

1 影响焊接变形的工艺因素

影响天线焊接效果的因素主要有降温曲线、焊料及工装方式。这3种因素都将导致天线焊接后产生结构变形，进而对天线电性能产生影响。下面对焊接过程中的主要工艺因素对焊接变形的影响加以说明。

1)在不同的降温曲线下，波导结构材料(主要为铝合金)的物性参数变化趋势不同。由于热膨胀系数在热加工过程中随曲线变化，导致焊接过程中，天线结构应力分布不均匀，累积形成残余变形。

2)焊料与铝合金的物性参数不同。在焊接过程中，由于焊料和铝合金的热膨胀系数不同，将在两者间产生较大的应力分布，从而引起焊接变形。同时焊料的熔点决定了焊接温度，也将影响到焊接变形。

3)工装方式不同。在高温阶段，铝合金会出现软化，工装能在一定程度上减小天线结构的软化变形。然而，不同的工装方式，导致天线结构在焊接过程中的受力情况不一样，会影响到天线结构的最终焊接变形。

2 焊接过程数值模拟与机电热分析

平板裂缝天线焊接过程是结构和热两个领域的能量和信息相互作用的过程，其为典型的结构-热之间的耦合问题。根据结构和热分析模型的差异，结构-热耦合分析主要有两种方法。

(1)异构模型分析

当结构分析采用有限元模型，热分析应用有限体积模型时，由于两种模型的网格信息不同，即为异构模型。为实现结构-热耦合分析，需要将热分析得到的温度场分布信息，通过插值法映射到结构有限元模型的单元上形成温度载荷，而后进行结构有限元分析。

(2)同构模型分析

当结构和热分析均采用有限元模型，并且两个模型的单元类型和节点信息一致时，可先进行热分析得到温度场分布，然后对该模型进行温度载荷下的结构有限元分析，实现热到结构的信息传递。

可见，同构模型分析方法在结构和热模型间信息传递较为简便和高效，本文采取该分析方法进行平板裂缝天线的焊接模拟。由于在天线焊接后会有结构变形存在，必然会对天线电性能产生影响。为此，本文除平板裂缝天线的结构-热耦合分析外，还需进行焊接变形的天线电性能分析，整个分析过程为机-电-热耦合分析，具体分析流程如图1所示。

图1 机-电-热分析流程

首先进行热分析，建立天线的热分析有限元模型，设置热膨胀系数等与温度相关的材料参数，施加热边界条件(包括换热系数、参考温度等)，设置求解方法及结果输出控制，施加热源分布进行瞬态求解，得到温度场分布。

其次进行结构分析，设置材料的结构参数(如泊松比、密度等)，施加结构边界条件(如约束等)，设置求解方法及结果输出控制，将温度场分布转换为单元温度载荷进行求解，采用热弹塑性理论，求得天线的残余应力分布和变形信息。其中焊料在分析过程中根据其刚度贡献情况采用生死单元技术。

最后进行天线电性能分析，使用结构分析时求得的天线变形信息，求得辐射缝的偏移量和偏转量，应用平板裂缝天线的机电两场耦合理论模型进行包括增益、副瓣电平在内的电性能计算。

2.1 热弹塑性有限元处理技术

热弹塑性有限元法可以在焊接热循环过程中动态地记录材料的热力学行为，详尽地掌握焊接残余应力和变形的产生及发展过程，因此是预测焊接变形的最重要和适应性最强的方法[1]。本文采用热弹塑性有限元法进行分析，以得到详尽的残余应力和变形在焊接过程中的变化情况。

焊接热弹塑性分析包括如下4个基本关系：应力-应变关系(本构关系)、应变-位移关系(相容性条件)、相应边界条件及平衡条件。在热弹塑性分析时需要做如下一些假定：材料的屈服服从米塞斯屈服准则；塑性区内的行为服从流动法则并显示出应变硬化；弹性应变、温度应变与塑性应变是可分的；与温度有关的机械性能、应力应变在微小的时间增量内线性变化[5]。

2.2 生死单元处理技术

在焊接过程中，焊料在温度超过熔点的时候会熔化成液态，此时焊料在模型中没有刚度贡献，焊料单元就可以被认为是“死亡单元”。单元生死选项并非真正的删除或重新加入单元，死单元在模型中依然存在，只是在刚度矩阵中将对应单元的影响项乘以一个很小的数(如ANSYS默认设置为1E-6)，使求解时其单元载荷、刚度、质量、阻尼、比热等接近0[6]。而当温度降低到焊料的熔点以下时，焊料开始凝固，凝固的单元就在有限元模型中“出生”，“单元出生”并不是将新单元添加到模型中，而是将以前“死亡”的单元重新激活。当一个单元被激活后，其单元载荷、刚度、质量等将被恢复为其初始值。这个过程是一个材料从无到有的过程，数值结果说明，使用有限元生死单元技术可以很好地模拟这个过程[7-8]。

在模拟焊接过程中，建模时必须建立完整的有限元模型，包括母材和焊料在内的整体模型。开始计算时先将焊料单元“杀死”，焊接过程的温度下降到焊料熔点时，再让这些单元“出生”。对焊料熔化过程中焊料的单元采用生死单元技术处理，可得到焊料在温度曲线下的应力和应变情况。

3 基于机电耦合模型的电性能分析

平板裂缝天线经过焊接后，结构将产生塑性应变及热应变等，这些应变都将带来天线结构变形。由于本文研究中未计入波导和缝隙机加工过程等引入的随机误差，通过焊接过程的数值模拟，得到的是天线结构受热加工过程引起的系统误差。从平板裂缝天线的电磁传播和辐射机理角度看，结构系统误差一方面影响了波导中电磁传播的路径，另一方面影响了电磁辐射空间的阵面边界。

在波导的电磁传播路径上，馈电网络变形主要为天线阵面辐射缝的面内偏移和偏转等系统误差，进而影响辐射缝电压分布。由于天线模型本身比较大，直接计算天线结构变形后的缝电压工作量较大。根据文献[9]，当辐射缝存在图2所示的面内偏移和偏转时，缝电压的变化量为

Δv=vn′-vn=

(1)

式中：vn和vn′分别为变形前后第n个辐射缝的缝电压；dn和dn′分别为变形前后辐射缝到所在波导边的距离；Δθn为变形后辐射缝的偏转角度；λ为工作波长；a和a′分别为变形前后辐射缝所在波导的宽度；i=arcsin(λ/2a)；i′=arcsin(λ/2a′)。

图2 辐射缝在波导中的变形示意图

在天线电磁辐射的边界上，结构变形主要为天线阵面上辐射缝的空间偏移和偏转等系统误差(图3)。辐射缝的偏移引起单元间的空间相位误差，偏转引起单元方向图变化，进而对天线电性能产生影响。结合辐射缝电压受馈电网络变形的影响关系式(1)，并应用平板裂缝天线的机电两场耦合模型[10]，天线结构变形后的远场方向图可表示为

exp[jk(rn+Δrn)·(sinθcosφ,

sinθsinφ,cosθ)]

(2)

式中：fn(θ-ξθn,φ-ξφn)为第n个辐射缝的单元方向图；ξθn、ξφn为第n个辐射缝的偏转量；θ、φ为空间点的观察方向；k为传播常数；rn和Δrn分别为第n个辐射缝的初始位置和偏移量。单元方向图的表达式见文献[11]。

图3 天线缝隙变形后的几何关系

4 某平板裂缝天线数值分析与讨论

现针对某机载平板裂缝天线，进行焊接过程和电性能分析。该天线整体尺寸为900 mm × 900 mm ×15 mm，包含激励、耦合及辐射波导层，且各层波导壁厚为1 mm，其中32根激励波导上各开有1个激励缝，辐射波导阵面上开有1 172个辐射缝，为多层空腔薄壁结构。

采用壳单元建立该天线结构的有限元模型，共包含420 991个单元和194 908个节点，其中母材部分单元总数为325 499，焊料部分单元总数为95 492，焊料位置如图4所示。数值模拟中使用的铝合金和焊料的材料参数列于表1和表2中。

图4 焊料位置情况图

表1 铝合金的物性参数

表2 焊料的物性参数

4.1 不同降温曲线的影响

焊接结束后总应变主要为塑性应变、热应变和相变应变三者残余量之和，由于这些应变都受到热载荷的影响，因此本文通过改变降温曲线，研究降温过程中降温曲线对这些应变的影响，以及变形对其相应天线电性能的影响。不同降温曲线是通过使天线在降温过程中改变其周围环境温度实现的。因此只要设定不同的时间-环境温度曲线，就能实现天线的不同降温曲线。焊接时一般将保温温度控制在低于母材固相线温度而高于焊料液相线温度。温度过高易产生母材熔蚀缺陷，温度过低易出现钎焊强度低，甚至焊料不全熔。钎焊保温时间以工件达到焊料液相线温度以后2 min左右为宜。保温时间过短，焊料不饱满圆滑，甚至不完全熔化。保温时间过长，则出现焊料漫流或漏焊[12]。当然，保温和冷却时间还受到零件大小和工装的影响。因此本文设计了3条降温曲线，如图5所示。

图5 降温曲线

由图5可知，曲线1是在2 100 s内，从600 ℃降至室温的降温过程；曲线2是在1 200 s内降至530 ℃，然后在2 400 s内从530 ℃降至室温的降温过程；曲线3是在2 400 s内降至530 ℃，然后在3 100 s内从530 ℃降至室温的降温过程。从曲线1到曲线3，降温速度越来越慢。曲线2和曲线3在高温阶段的降温速度比较慢，是为了使天线在高温时的温差比较小，以免对晶相产生影响。不同的降温曲线影响材料晶相生长，引起天线在降温过程中的物性参数产生变化。目前许多工程材料尚缺乏高温时的各种物性参数[13]，经过试验测得当冷却速率增大时，材料热膨胀系数增大[14]。针对图5的降温曲线假设了几组不同热膨胀系数，如图6所示。

图6 母材热膨胀系数α随温度的变化

图6中，α1、α2、α3分别为降温曲线1、2、3对应的母材热膨胀系数。不同降温曲线在整个模型上产生的温差和最大应力如图7和8所示。

图7 不同降温曲线在模型上产生的温差

图8 不同降温曲线在模型上产生的最大应力

由图7可见，降温最快的曲线1产生的最大温差达到1.9 ℃，降温最慢的曲线3产生的最大温差只有1.1 ℃。即降温曲线越平缓，模型中的最大温差越小，可以使模型中的温度梯度比较均匀。从降温曲线1和3的温差曲线可知，增加降温时间，降温曲线会变缓，这样可使天线内部的热量通过传导扩散到散热表面，对天线内部的温度下降比较有利。

由图8可知，天线在降温过程中，最大应力随着焊料的凝固而增加，在温度降到室温时，应力达到最大值。高温阶段的最大应力会随着降温曲线的变化而变化，高温阶段的降温时间比较长，焊料的凝固时间也较长，因此同样的最大应力出现的时间也发生了变化。

在不同降温曲线下，天线钎焊后的最终残余应力、变形及辐射面RMS(均方根误差)值列于表3。

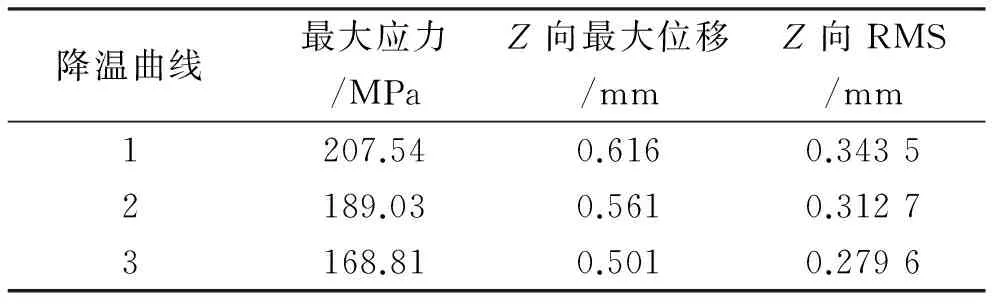
表3 不同降温曲线下最终残余应力及变形

由表3可知，降温越慢，天线结构在整个降温过程中的温度分布越均匀，能明显改善天线焊接后的残余应力和变形。如降温最快的曲线1最终的残余应力为207.54 MPa，降温最慢的曲线3最终的残余应力为168.81 MPa，减小了18.7%。同时，降低降温速率，对改善变形也很明显。如相对曲线1，曲线3最终Z向最大位移减小了0.115 mm，改善了19.1%，表面RMS则减小了0.063 9 mm，改善了18.6%。

从天线结构变形中提取出辐射缝的面内偏移量和偏转量，并应用公式(1)计算出缝电压的变化量。表4给出了降温曲线2下的情况，其中天线工作频率为10 GHz。

表4 降温曲线2下的辐射缝信息

由表4可知，平板裂缝天线焊接后结构变形引起的面内偏移量较小，尤其是辐射缝的面内偏转量几乎可以忽略，这与辐射缝位于同层波导上有关。结合表3的法向位移(Z向)信息，应用公式(2)计算天线远场方向图的变化情况，并提出增益损失和副瓣电平情况列于表5。

表5 不同降温曲线下的电参数

由表5可知，降温过程慢，最终的表面RMS较好，天线电性能也相应变好，与理论一致。因此，随着降温曲线变慢，天线的电性能随之变好，降温曲线3的增益损失比降温曲线1改善了22%。

4.2 不同焊料的影响

选用合理的焊料能提升焊接后天线的强度、减小变形。本文选取了3组焊料，根据已有的铝基焊料，如Bal86SiMg, Bal88SiMg, Bal89SiMg等，它们的热膨胀系数与母材分别相差约15%、10%、5%[15]。焊接模拟分析时，采用了3种不同的焊料热膨胀系数，具体信息列于表6。其中低胀是指焊料的热膨胀系数低于母材的热膨胀系数，得到热胀系数比分别为15%、10%、5%的情况。在不同热胀系数比的情况下，分析结果列于表7。

表6 焊料的热膨胀系数

表7 不同热胀系数比下的最终残余应力和变形

由表7可知，Z向最大变形和表面RMS随着热胀系数比的减小而减小。这是由于热膨胀系数差异越小，降温过程中焊料与母材的收缩量趋于一致，使得结构变形减小。在焊料热膨胀系数接近母材热膨胀系数时，由于焊料的收缩量变大，焊料受到的压应力随之减小。

不同热胀系数比的情况下，焊接后的天线增益损失和副瓣电平情况列于表8。

表8 不同热胀系数比下的电参数

由表8可知，随着热胀系数比的减小，天线的增益损失和副瓣电平减小，如低胀5%的增益损失比低胀15%减小了18.8%。这说明降低热胀系数比可有效改善焊接后的天线电性能。

4.3 不同工装方式的影响

工装方式也是影响焊接后结构变形的关键因素之一。由图9的工装示意图可知，通常平板裂缝天线的辐射层阵面置于云母之上，弹簧的夹紧力施加到其背面，具体包括辐射层、耦合层及激励层的背面。根据弹簧夹紧力在天线背面施加的位置和方式，本文设计了3种工装方式，如图10、11和12所示。

图9 天线焊接过程中工装示意图

图10 工装方式1

图11 工装方式2

图12 工装方式3

在图10的工装方式1中，通过连接弹簧的平面钢板将夹紧力施加到平板裂缝天线的背面。由于激励层所在位置高于其他波导层，夹紧力仅施加到激励层的背面。而仅压激励层，会导致焊接面积比较大的辐射层没有被压紧，容易出现虚焊问题。这里主要用这种工装方式与其他方式做比较。

将工装方式1的钢板拆分成多块，部分钢板可置于辐射层背面，形成工装方式2(图11)。这样夹紧力不仅施加在激励层背面，还包括辐射层的背面，可使工件背面受力较为均匀。

进一步将工装方式2的多块钢板拆分成多个小圆板，每个弹簧连接一个小圆板，形成工装方式3(图12)。由于天线的受力面积相对工装方式2减少，其受力情况不如工装方式2均匀。在这3种工装方式中，当支架刚度不够时，可以添加横梁来加强刚度。由于这3种工装方式的压头都与装在支架上的弹簧连在一起，因此不会影响熔盐的流动。

根据文献[16]和文献[4]，选取弹簧夹紧力在0.005～0.01 MPa之间，分别为2.5e-3、5e-3、7.5e-3、10e-3 MPa 4种。

在进行焊接模拟时，降温曲线为图5中曲线1，热胀系数比为低胀15%，不同工装方式的分析结果见表9、10、11及12。

表9 工装1不同夹紧力下的变形

表10 工装2不同夹紧力下的变形

表11 工装3不同夹紧力下的变形(7个压头)

表12 工装3不同夹紧力下的变形(18个压头)

由表9～12可知：

1)在夹紧力小于0.01 MPa时，天线焊接后的效果都是比较理想的，最终天线辐射面的RMS都能保持在0.05 mm左右。在夹紧力达到0.01 MPa时，天线焊接后的最大变形和表面最终RMS出现明显变化，因此在使用工装方式2或3时，最大夹紧力应控制在0.007 5 MPa左右。

2)由表10～12可知，在夹紧力相同的情况下，使用工装2或3两种不同的压头分布，受力均匀的工装2的计算结果较好。

3)由表11和12可知，在同一种工装形式下，增加压头的数量并不一定能改善天线焊接效果。当把工装2视为工装3增大压头的情况时，只有当天线受力分布均匀时，才能改善天线的焊接效果。

4.4 各因素的影响比重

通过分析各工艺因素在焊接过程中对焊接结果的影响比重，可在实际焊接过程中控制这些关键工艺因素，改善焊接后的天线结构变形，降低对天线电性能的影响。为此，设定各工艺因素影响焊接变形最小时的参数为最优工况，并将其作为基准工况。然后分别改变各参数至最差参数，计算焊接后的天线阵面RMS值。与基准工况的RMS值进行对比，求得各因素的影响量和比重。模拟过程中选择了表13所示的不同工况参数，得到天线焊接后的阵面RMS值、影响量及比重。

表13 不同工况参数

各工况下阵面RMS值的影响量计算公式为：

式中：x0为基准工况的RMS值；xi为各工况的RMS值。影响量给出的比重计算公式为：

wi=Δxi/(Δx1+Δx2+Δx3)×100% (i=1,2,3)

由表13可知，降温曲线对天线的焊接变形影响最大，占50%；热胀系数比次之，占44.8%；而改变工装方式的影响最小。可见，在降温过程中，控制降温曲线和选择合适的焊料能比较明显地改善天线焊接后的变形，进而改善其电性能。

5 结束语

通过对平板裂缝天线焊接工艺的数值模拟，获得了不同的降温曲线、热胀系数比及工装方式等工艺因素对天线结构焊接后变形、残余应力及天线电性能的影响。同时分析了不同工艺因素对焊接变形的影响比重。本文的研究工作可为平板裂缝天线的工艺参数的选择提供借鉴。

需指出的是，本文所得结果是基于3层波导的机加工不存在误差的情况，这是不符合工程实际的。下一步工作应在模型中加入各层波导的加工误差，研究可在多大程度上降低对波导加工精度的要求，从而降低研制和制造成本。

[1] 王岩, 汤小红. 铝合金焊接应力与变形数值分析综述[J]. 焊接技术, 2012, 41(1): 1-4.

[2] 郭利军. 微波器件的真空铝钎焊加工工艺研究[D]. 西安: 西安工业大学, 2007.

[3] 陈晓梅, 李亨昭, 陈敏. 整体拼装平板裂缝天线组件结构工艺研究[J]. 现代雷达, 2006(3): 95-98.

[4] 黄剑波. 机载雷达平板裂缝天线盐浴钎焊工艺研究[D]. 南京: 南京理工大学, 2010.

[5] 张庆移. 6061铝合金薄板的焊接变形数值模拟[D]. 上海: 上海交通大学, 2004.

[6] 刘学武, 郭彦林. 考虑几何非线性钢结构施工力学分析方法[J]. 西安建筑科技大学学报: 自然科学版, 2008(2): 161-169.

[7] MASUBUCHI K. Analysis of Welded Structures: Residual Stresses, Distortions and Their Consequences[M]. Pergamon Press, 1980.

[8] LINDGREN L, KARLSSON L. Deformations and stresses in welding of shell structures[J]. International Journal for Numerical Methods in Engineering, 1988, 25(2): 635-655.

[9] COETZEE J C, JOUBERT J, MCNAMARA D A. Off center frequency analysis of a complete planar[J]. IEEE Transactions on Antenna and Propagation, 2000, 48(11): 1746-1755.

[10] 宋立伟. 天线结构位移场与电磁场耦合建模及分析研究[D]. 西安: 西安电子科技大学, 2011: 41-45.

[11] MAXUM B. Resonant slots with independent control of amplitude and phase[J]. IEEE Transactions on Antennas and Propagation, 1960, 8(4): 384-389.

[12] BACHORSKI A, PAINTER M J, SAMAILES A J, et al. Finite element prediction of distortion during gas metal arc welding using the shrinkage volume approach[J]. Journal of Materials Processing Technology, 1999, 8(60): 405-409.

[13] 武传松, 陆皓, 魏艳红. 焊接多物理场耦合数值模拟的研究进展与发展动向[J]. 焊接, 2012(1): 10-22.

[14] 纪宏志, 袁林, 单德彬. 不同冷却速率下7A09铝合金冷却收缩行为研究[J]. 材料科学与工艺, 2011, 19(5): 17-20.

[15] 程鹤. 平板裂缝天线的钎焊变形分析及研究[D]. 西安: 西安电子科技大学, 2012: 33-34.

[16] 杨少木, 袁体松. 铝合金大板拼焊配重压紧法[J]. 电焊机, 1993(1): 36-37.

肖志城(1987-)，男，硕士研究生，主要从事平板裂缝天线机-电-热耦合分析。

宋立伟(1981-)，男，副教授，主要从事电子装备机电耦合理论及应用研究。

Numerical Simulation of Manufacturing Errors from Braze Welding for Planar Slotted Waveguide Antennas and Its Effects on Antenna Electromagnetic Performance

XIAO Zhi-cheng，ZHU Min-bo，SONG Li-wei，DUAN Bao-yan

(KeyLaboratoryofElectronicEquipmentStructureDesign,MinistryofEducation,XidianUniversity,Xi′an710071,China)

The effect of braze welding on the electromagnetic performance of planar slotted waveguide antennas is studied based on inter-disciplinarity. Firstly, according to thermal elastic-plastic theory and birth-death technique, the impact of three factors including cooling curve, solder and clamping method on the antenna′s residual stress and deformation is simulated. Secondly, on the basis of fields coupled mathematical model between structural displacement field and electromagnetic field, the influence of manufacturing errors from braze welding on the antenna′s electromagnetic performance (gain, side lobes, etc.) is explored. Finally, the theory and method are applied to an airborne planar slotted waveguide antenna, some satisfactory results are obtained.

planar slotted waveguide antenna; soldering distortion; cooling curve; solder; clamping method; electromagnetic performance

2014-05-12

国家自然科学基金资助项目(51365003，51405364)；中央高校基本科研业务费项目

TN823+.24; TG457

A

1008-5300(2014)05-0041-07