北师大版教材教学的一点思索

颜巍

随着新一轮课改的深入，教师的教育教学方法发生了很大的变化，新课程强调教学过程师生交往、共同发展的互动过程，注重培养学生的独立性和自主性.让学生在实践中学习，使学习成为在教师指导下主动的富有个性的过程，与新课程理念相配套的新教材充分体现了这点，特别是“几何”部分拓广为“空间与图形”与以前的教材有很大的不同，因此认真研究数学课程标准对教材的要求，在新教材教学实践有如下体会.

课程改革是在吸纳原有教材精华的基础上，结合并凝练实际教学中的优秀经验，并且将这些经验纳入课本进行理论上的创新.数学课程标准提出，数学教学是不能够脱离学生实际经验的情况下进行的，要和学生的德智发展同时进行.执教进行的过程中，教师要提前准备好丰富生动的教学内容，这些内容最好是能够与学生熟悉与生活的环境息息相关，以拉近学生和课程之间的心理距离.在讲授课程时，还应注重调动学生的兴致与疑惑，以达到让学生主动进行思考、积极思考的目的，在这一互动式的教学中，教师也能够收得更丰富的教学经验.

在教学过程中，教师可以从以下几个方面对学生进行培养.

一、在探求新知时，引导学生操作实验

在教学过程中，常常是教师从头到尾和盘托出，把定理、公理、性质等讲完，学生会应用运用它们解决问题这一课就算结束，但在新课程中，大量使用了“探索……”，因此，不能教师一手包办.

例如，在讲“直线公理”时，教师可以请学生思考身边的实例：建筑师傅是如何确定高楼建造是否竖直的？然后让学生动手做实验：用一个图钉将一根小薄木条钉在墙上，请一位同学转动木条，并观察现象，然后再在木条上加上一个图钉再转动观察现象，通过动手实验，总结出直线公理并用它解释实践生活中的一些操作的原理，接着再用它解决问题，如怎样使一列桌子摆列整齐等.

又如，在讲“正方体的平面展开图”时，先分小组动手沿着棱剪开正方体后展开，组内看看有几种不同展开图，再到组与组之间的交流，把不同的展开图贴在黑板上共可收集到11种不同展开图，然后让学生思考展开时共剪开正方体的几条棱？为什么？最后由六个相同的小正方形折起来能否折成正方体？探讨能折成正方体的条件.这种经由学生亲自实践的教学方法，能让学生对知识的记忆更加深刻，更重要的是可以引导学生对待问题的态度：只有积极地思考与着手尝试才是解决问题的不二法门.

二、设置凝问，让学生敢于提出问题

在数学教学中，学生亲自参与实践是最有效的方法.

例如，在讲“三角形三边关系定理”时，教师可先提出疑问：是任何长度的三条线段都能围成三角形吗？开始时学生的观点多是肯定与中立的，这时给每组学生分发事先准备好的塑料棒，通过学生的实践让他们判断问题的答案，学生可能会发现并不是任意的长度搭配都能形成三角形，那么在什么样的条件下，线段才能围成所需形状呢？类似的可以进行衍伸的测验：在一个△ABC中，小蚂蚁从一个顶点爬到另外一个顶点，有几种可行的路径呢？每条路线的长一样吗？小虫从B出发沿三角形的边爬到C有如下两条路线：方法1：从B→C；方法2：从B→A→C.从B沿边BC到C的路线长为线段BC的长，从B沿边BA到A，从A到C的路线长为BA+AC，经测量BA+AC>BC，即两路线不一样长，提出问题：在同一个三角形中，任意两边之和与第三边有什么关系？通过学生动手和实验容易得到上述结论，同时指出：能否利用以前所学知识说明这结论，这样安排比直接告诉学生三角形的任意两边之和大于第三边容易接受得多.

三、创设现实情境，提供给学生主动探究空间

课程改革的其中一个重要目标是培养学生有效能、有效率的学习方式，尤其是在数学学习中，因为数学不单单是纯粹的记忆力的需要，更多的是要激发学生的实践及逻辑能力，在自主思索与动手的过程中自然而然的吸收新的知识.

例如，在讲“点、线、面三种基本要素转化”时，可以简单引导学生把铅笔或粉笔的笔尖当做一个点要素，当移动笔尖时，就逐渐形成了线要素.把汽车雨刷看做一条线，它在挡风玻璃上运动时有什么现象，钟表上的分针在运动过程中有什么现象？长方形纸片绕着它的一边旋转，形成了什么？通过现象分析得出结论，这样从学生己有的生活经验和已有的知识出发，给学生提供“现实的、有意义的、富有挑战性”的学习材料，提供充分的数学活动和交流的机会，引导学生在“做数学”的活动中和在自主探索的过程中获得知识和技能，掌握基本的数学思想方法，通过动手操作和主动参与，让学生在观察、操作、猜想交流中认识图形，发展空间观念，创设情境使学生积极参与到数学活动中来，对数学产生好奇心和求知欲.

教师可给学生留下测量学校旗杆高度的题目，让学生进行分组，自由讨论可行的测量方案，有的学生可能会想要将旗杆放平直接量取，有的学生可能会根据学过的比例法则，设立参照物分别量取旗杆和参照物的投影长度，进而进行计算，教师所需要做的就是正确引导，让学生思考这些方案的难易度、准确度与可行性.让学生亲自实践时也会遇到各种情况：如旗杆的影子不在水平地面上，而是有部分在其它建筑物上不能直接测量到旗杆底部或者是下雨天没有太阳怎样测量，从而进一步激发学生遇到具体情况时要能找到解决问题的办法.可见，只要给学生一点空间，他们就会把它放大，这就是实践与创新，这才是学有价值的数学.

在课程改革的过程中，学生的实践经验是备受关注的一个关键原则.学习的过程不仅仅是书本知识的获得，还应是学生的综合能力，如逻辑、情商、观念等多个层次的同时提升，鼓励学生的实践能力能够让学生收获更多，全方位地提高自身.

四、通过动手实验、操作形成解决问题的能力

数学课程标准这一新标中重点提出学生获得知识途径的更新，从传统的讲授变为互动的实践，学生收获的不单单中知识，更重要的是学习方法与思考方式，对于以后的深远学习乃至生活都有更多的益处.在一些习题中对于剪、拼、旋、叠的问题作为一个亮点出现，解决这类问题的有效方法就是通过实验操作探究变化过程存在的规律问题，揭示数学问题的变化过程，能给学生以强烈的直观效果，活跃学生的思维，从而可导出解决问题的特殊化方法.

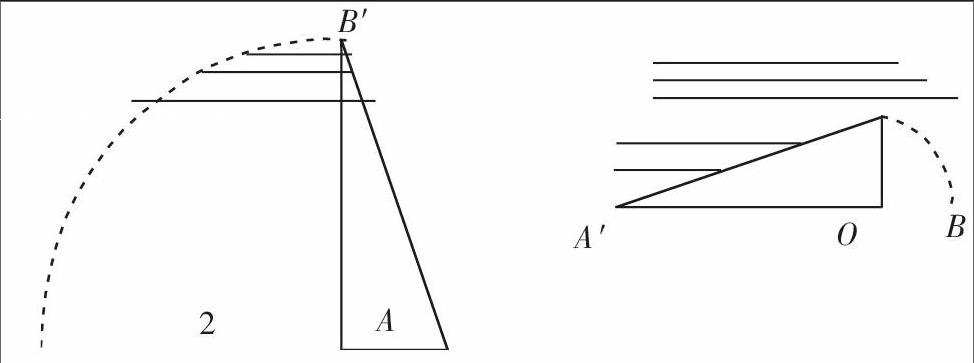
例如，如图1，在△AOB中，OA=3cm，OB=1cm.将△AOB绕着O点逆时针方向转动90°，形成新的图形△A′OB′，那么在这一旋转过程中，AB扫过的区域（即图中阴影部分）的面积是cm2.

图1

此例若直接求阴影部分面积困难极大，但是在大量的有意识的训练下，大部分学生都形成了一定能力，他们都会动手操作，剪一个△OAB让它绕O逆时针旋转，在多次旋转过程中认真观察O，B，A三点的变化情况，发现阴影部分面积等于扇形OAA′与扇形OBB′面积之差，使问题简单解决.

总之，“授人以鱼，不如授人以渔”.只要在教学实践中坚持新课程理念，真正以学生为本，把课堂还给学生，给学生以足够的时间和空间，让学生独立思考把握时机，让学生的多种感官参与学习，通过动手操作和实验等手段探究知识，从中学到分析问题、解决问题的能力，就能培养学生的能力和创新精神.