基于MFOA和LW的混沌时间序列鲁棒模糊预测

刘福才，窦金梅，王树恩

(燕山大学 电院工业计算机控制工程河北省重点实验室，河北 秦皇岛 066004)

混沌是一种出现在确定性系统中的貌似无序类似随机的复杂现象。随着混沌理论研究的不断深入及其在通信信号处理、自动控制与电子对抗等领域中的广泛应用，混沌时间序列的建模与预测已成为混沌理论研究领域中一个非常重要且极为活跃的方向。模糊集合理论自1965年创建以来，已得到广泛研究，并在许多领域得到了应用。基于模糊系统的混沌时间序列预测已取得丰硕成果，如文献[1]中提出基于模糊树模型辨识混沌系统， 文献[2]提出了一种模糊竞争学习算法的在线辨识方法来预测混沌动力系统，文献[3]提出一种鲁棒模糊聚类算法预测混沌时间序列，增强了模型的抗干扰能力。果蝇优化算法(fruit fly optimization algorithm,FOA)是一种新的元启发式算法[4]，具有编程简单、全局优化、计算速度快等优点，目前在外贸出口预测[5]、企业经营业绩评估[6]、船舶操纵响应模型的辨识[7]等方面都得到很好的应用，将FOA应用于模糊模型的参数辨识是一个全新方向，为模糊辨识参数优化提供了一条新途径。最小Wilcoxon (least Wilcoxon， LW)算法[8]可以在有例外点的情况下实现对线性系统的辨识，有较强的鲁棒性，其应用已被很多学者重视。如文献[9]基于最小Wilcoxon T-S模糊模型，对非线性函数进行逼近；文献[10]用神经网络和粒子群优化算法对非线性复杂系统进行了基于LW方法的鲁棒辨识；文献[11]中，用W-范数和粒子群算法对前馈有源噪声系统进行鲁棒控制，改善了传统的x滤波最小均方误差(FxLMS)算法对扰动敏感的问题。针对混沌时间序列的建模与预测问题，考虑到上述方法结合的优点，本文提出了一种基于修正型果蝇优化算法(modified fruit fly optimization algorithm， MFOA)和LW的混合算法的模糊预测方法，分别用来优化模糊模型的前提和结论参数，实现对模型参数的全局优化。

1 模糊模型与参数优化编码

采用基于T-S模糊模型的混沌时间序列预测方法，一个模糊逼近器由数条模糊规则组成，T-S模型的第i条规则描述为[12]

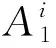
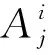
前件模糊划分采用高斯型隶属函数:

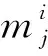
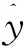
(1)

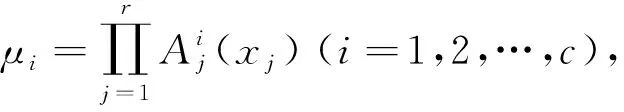
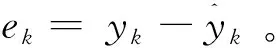
图1 模糊辨识的结构框图Fig.1 Diagram of fuzzy identification

在一个模糊系统中，如果有r个输入变量，c条模糊规则，那么对于MFOA，食物在搜索空间的位置可由向量f表示:

式中：m和σ分别为隶属函数的中心和宽度。f为2r×c维向量，此即优化参数的编码。

2 MFOA与LW方法

2.1 修正型果蝇优化算法(MFOA)

FOA是基于果蝇的觅食行为推演出寻求全局优化的新方法。作为一种昆虫，果蝇在感官知觉上，尤其是嗅觉和视觉上优于其他生物。果蝇的嗅觉器官能够搜索到漂浮在空气中的所有气味，甚至能够嗅到40 km外的食物源，在飞近食物的位置后又可以利用敏锐的视觉发现食物和同伴聚集位置，并飞向该方向[4]。

虽然FOA计算简单，易于编程和理解，但在随机初始化果蝇的位置距食物较远时，FOA有可能不成熟收敛，容易陷入局部最优值。为了得到较FOA性能更好的算法，文献[13]提出一种带逃离局部最优因子β的修正型果蝇优化算法(MFOA)，它通过一种数学转换来扩展味道浓度值的分布，从而避免陷入局部最优，同时提高收敛速度，获得高质量的解。

基于果蝇搜寻食物的特点，MFOA主要有以下几个步骤[13]:

1) 给定种群个体数目(sizepop)和最大迭代次数(maxgen)，随机初始化果蝇的初始位置(IntiX_axis,IntiY_axis)。

2) 给出果蝇个体利用嗅觉搜寻食物的随机方向和距离(Xi,Yi)，如式(2)所示。

(2)

3) 估计果蝇与原点之间的距离(Disti)，计算味道浓度判定值(SMi)。

SMi=1/Disti+β

式中：β为逃离局部最优因子，它的2种表达式如式(9)和(10)所示:

β=g×Disti

(3)

β=λ×IntiX_axis orλ×IntiY_axis

(4)

式(3)中g为服从均匀分布的随机变量，式(4)说明β与群体的随机初始化相关，λ是一个常数。

4) 将SMi代入味道浓度判定函数(Fitness function)求出该果蝇个体位置的味道浓度(Smelli)。

Smelli=Function(SMi)

5) 找出此果蝇群体中味道浓度最高的果蝇。

[bestSmell bestIndex]=max(Smelli)

(5)

6) 保留最佳味道浓度值，最佳味道浓度判定值与相应果蝇x、y坐标，果蝇群体中其他果蝇利用视觉向该方向飞去。

Smellbest=bestSmell

Sbest=SM(bestIndex)

IntiX_axis=X(bestIndex)

IntiY_axis=Y(bestIndex)

7) 迭代寻优，重复执行2)～5)，并判断味道浓度是否优于前一次迭代味道浓度，若是，则进入6)。

在MFOA算法中，以味道浓度值最大为迭代标准，所以将建模的均方根误差(RMSE)的倒数作为果蝇味道浓度判断函数，而得到的对应的最佳味道浓度判定值即作为参数的潜在最优解。所以，果蝇味道浓度判定函数为

Function=1/(RMSE+ε)

(6)

式中：ε=10-10，用于避免零作为除数(RMSE为零时)。

2.2 最小Wilcoxon方法

W-范数考虑的是误差值的顺序或位置而不是其幅值。考虑向量v=[v1v2…vl]，其中l是向量的长度，那么v的W-范数定义为[8]

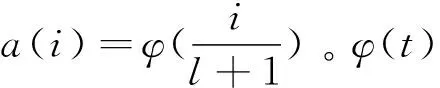
文献[15]中给出了很多记号函数，这里选择最常用的一个，即

(7)

由于Wilcoxon范数是基于统计参数的一个排序，所以在W-范数中，需要采用点或块的学习策略来计算一个排序。基于点的学习方法耗费时间，并且在实时应用中难于实现。然而，由于权值在每个输入样本块输入后就进行更新，所以基于块的学习方法速度更快。因此本文采用基于块的学习方法。

由式(1)可得出模糊系统的输出

[w1w1x1...w1xr...wcwcx1...wcxr]×

将K对输入输出数据代入上式可得

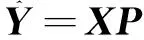
(8)

式中：P是L=(r+1)c维结论参数向量；Y、X是K×I、K×L的矩阵。

为了求出结论参数P，这里应用LW方法来进行辨识。每次迭代的输入向量相同，权值不断更新，随着每次实验，权值达到收敛。

辨识误差向量为

E=[e(1)e(2) …e(K)]Τ

式中：误差的第k个元素定义如下:

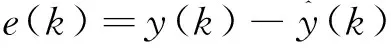
(9)

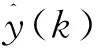
式(9)用矩阵表示为

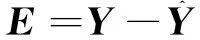
(10)

目标函数定义为

(11)

式中：s(k)是通过记号函数φ(t):[0,1]→R定义的联合记号函数，记号函数的选择如式(7)所示。ek表示的是将向量E中的值e(k)按升序排列后的误差值:

ek≤ek+1，1≤k≤K

(12)

(13)

式中：R{e(k)}表示e(k)在向量E中的顺序号。

式(13)写成矩阵形式为

(14)

式中：R表示R{e(k)}在k=1,2,…,K时所形成的一个矩阵。

结论参数P的更新公式可以写成

P=P+ΔP

(15)

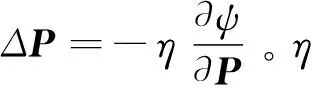
(16)

式中s、X如前所述。

所以，LW算法可以由等式(8)、(10)、(14)～(16)来完整描述。

2.3 MFOA-LW混合算法

将MFOA和LW算法以一种组合的形式来训练含有例外点的T-S模糊模型。本文根据经验给定模糊规则数和输入变量，采用模糊网格对角线法划分前提结构[14]，MFOA算法用来优化模型的前提参数(即隶属函数参数)，果蝇寻找到的每一个最佳味道浓度判断值都是一个潜在的前提解。前提结构和参数确定以后，下一步工作就是用LW方法辨识结论参数。

MFOA-LW混合学习算法辨识T-S模糊模型的学习步骤如下:

1) 由目标系统得到一组输入输出数据对；

2) 设计一个模糊逼近器(其中包括输入变量个数的选择和模糊规则数的确定，模糊空间的划分)；

3) 随机初始化果蝇的初始位置，根据第2.1节中MFOA算法的步骤计算初始果蝇群体中最佳味道浓度判定值，将其作为模糊模型的初始前提参数；

4) 输入训练数据集到图1所示的模糊逼近器，用2.2节的LW方法计算T-S模型结论参数P；

5) 用结论参数P和训练数据集计算模型的输出；

6) 用式(6)计算果蝇的味道浓度值(类似适应度函数)，并根据式(5)得出果蝇最优味道浓度值及相应的判定值和果蝇相应位置，更新种群中果蝇的位置，根据第2.1节中MFOA算法的步骤计算此次迭代的最佳味道浓度判定值；

7) 返回到4)，直到满足终止条件(MFOA算法迭代终止)。

3 仿真研究

自1977年Mackey和Glass发现时滞系统中的混沌现象[15]以来，时滞混沌系统便引起了人们的广泛关注，并常常用其作为检验非线性系统模型性能的标准。应用本文的MFOA-LW方法对Mackey-Glass混沌时间序列进行建模与预测，以此来说明本文方法的有效性和鲁棒性。

Mackey-Glass混沌时间序列用微分方程描述为

(17)

此方程描述的是在正常呼吸和不正常呼吸时动脉的CO2浓度，属于一类有混沌行为的时延方程。其中τ为时滞参数，τ≥17时，方程(17)处于混沌状态，其分形维数近似为2.1，并且τ值越大，混沌程度越高。图2(a)和图2(b)给出了τ=17时的混沌时间序列及其相图，初始条件x(0)=1.2。本文中，τ=17,a=0.2,b=0.1。混沌时间序列预测的目标是用t时刻以前的值预测t+p时刻的值。通常，取间隔为Δ的D个历史时刻的值，建立[x(t-(D-1)Δ) …x(t-Δ)x(t)]T到x(t+p)的映射关系。

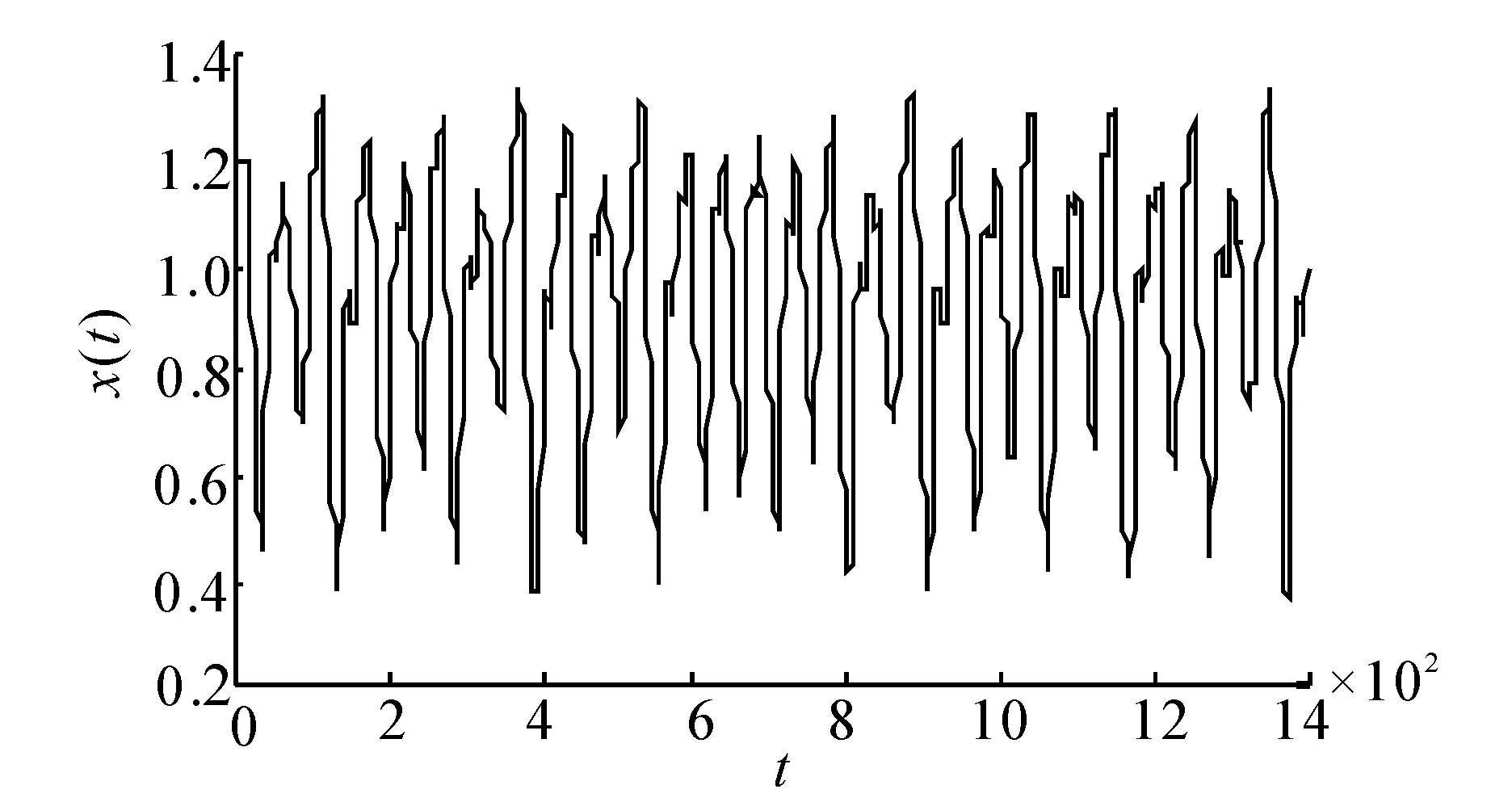
(a) Mackey-Glass混沌时间序列

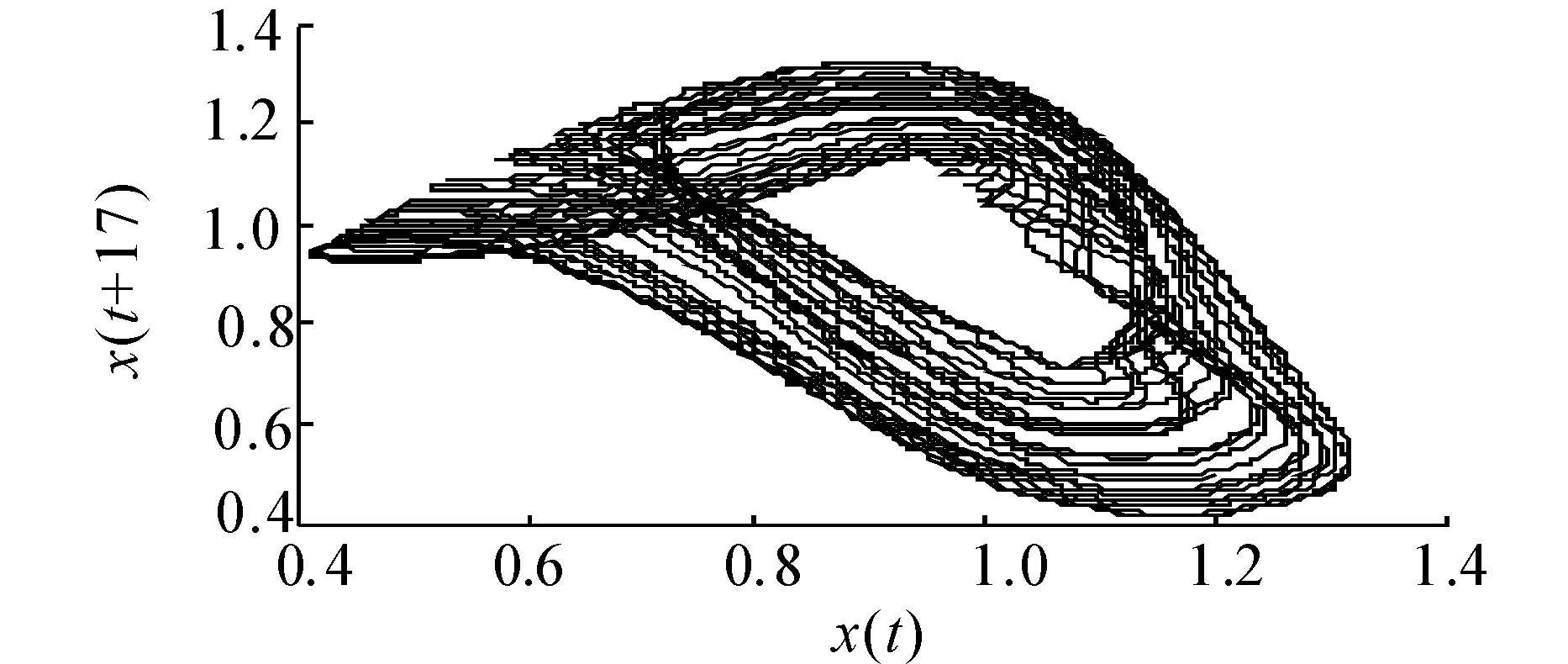
(b) 系统相图图2 τ=17时Mackey-Glass时滞混沌系统Fig.2 Mackey-Glass time delay chaotic system whenτ=17

本文中取D=3,Δ=1,p=1，那么模型输入向量X为[x(t-2)x(t-1)x(t)]Τ，输出Y为x(t+1)。x(0)-x(17)赋初值为1.2。在t=117和t=617之间采集500个数据作为建模数据。模糊划分数c=4。

MFOA参数:最大迭代次数maxgen=500，种群数目sizepop=40。随机初始化果蝇群体的位置区间为[0,20]，迭代过程中果蝇搜寻食物的随机飞行方向与距离区间为[-5,5]，β采用式(3)形式，其中g定义为在[-0.5,0.5]上均匀分布的随机变量。

首先验证MFOA算法在辨识方面的优越性，将MFOA算法的优化结果与粒子群算法(PSO)、菌群优化算法(BFO)进行比较。分别采用MFOA，PSO，BFO优化模糊模型的前提参数，递推最小二乘法(RLS)优化结论参数[18]。本文所选参数均为相关文献常用参数。

PSO算法参数为：学习因子c1=1,496 2，c2=1.496 2；惯性权重ω=0.729 8；最大迭代次数MaxDT=1 000；初始化群体个体数目N=40。

BFO算法参数：种群数目S=100，趋向性操作数Nc=100，在同一方向上前进的最大限制步数Ns=4，复制操作数Nre=8，迁徙操作数Ned=2，细菌迁徙概率Ped=0.5，趋向性行为步长C(i)=0.1，细菌间引力深度dattractant=0.01，引力宽度wattractant=0.2，斥力高度hrepellant=0.01，斥力宽度wrepellant=10。

RLS算法初始条件为：P0=0,S0=αI，α是一个很大的实数，0<α<，本文取α=104。

表1给出了3种优化算法的参数和仿真结果的RMSE。图3～5分别给出仿真结果的逼近曲线和误差曲线。由仿真结果可以看出，较其他算法相比，MFOA-RLS算法辨识精度高，计算量小，能够有效预测混沌时间序列。

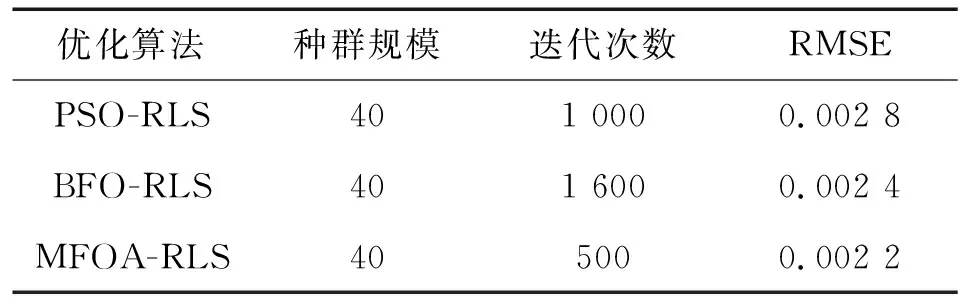
表1 不同优化算法的建模结果(RMSE)

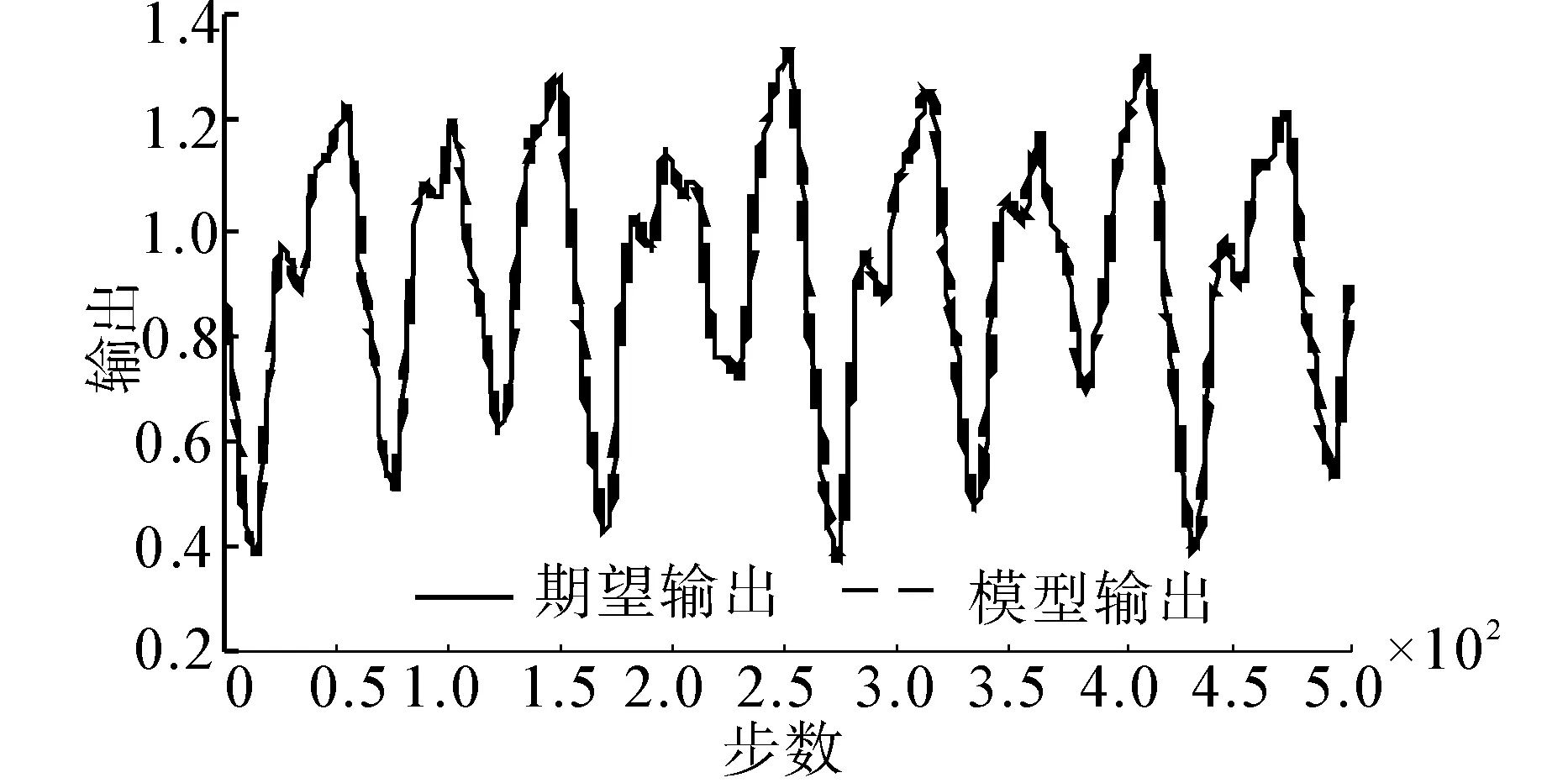
(a)建模逼近曲线

(b) 建模误差曲线图3 MFOA-RLS预测结果Fig.3 Prediction result of MFOA-RLS

(a)建模逼近曲线

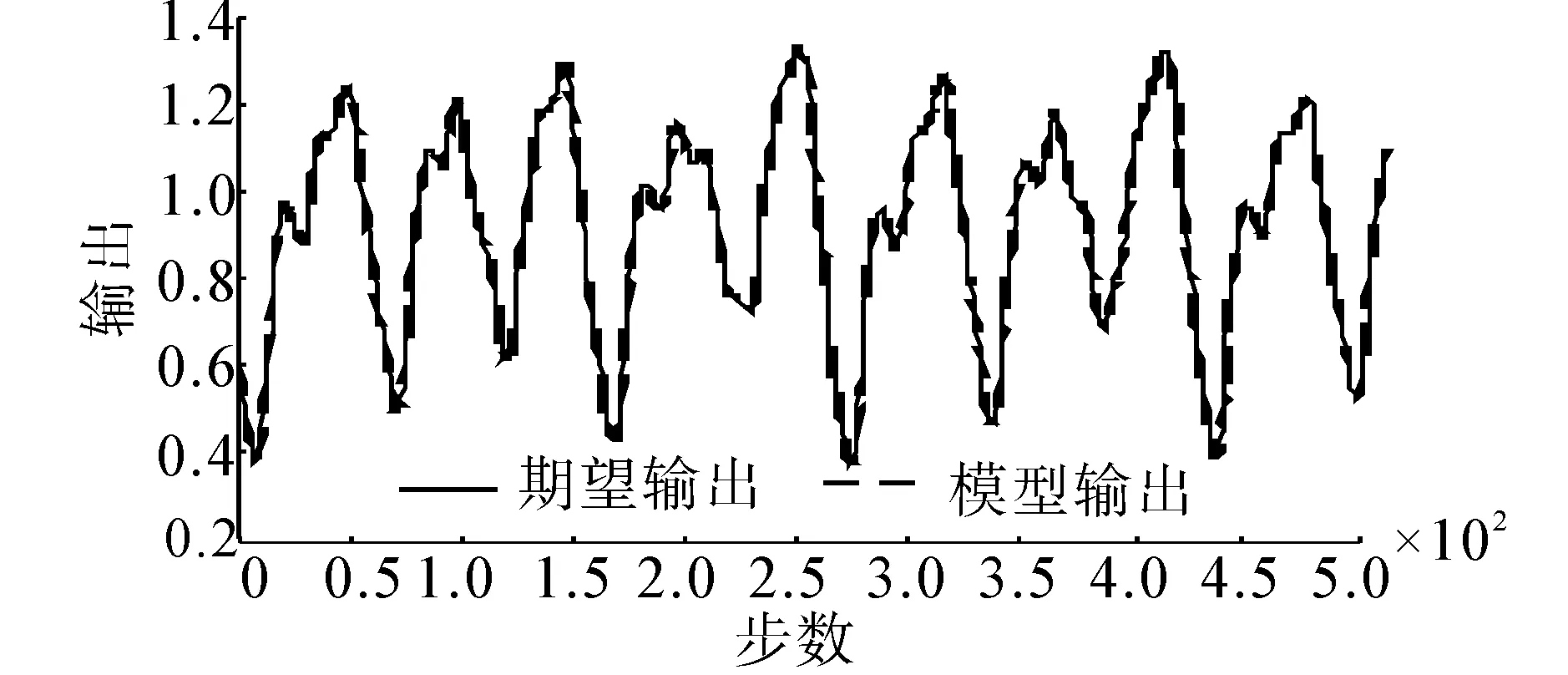
(b) 建模误差曲线图4 PSO-RLS 预测结果Fig.4 Prediction result of PSO-RLS

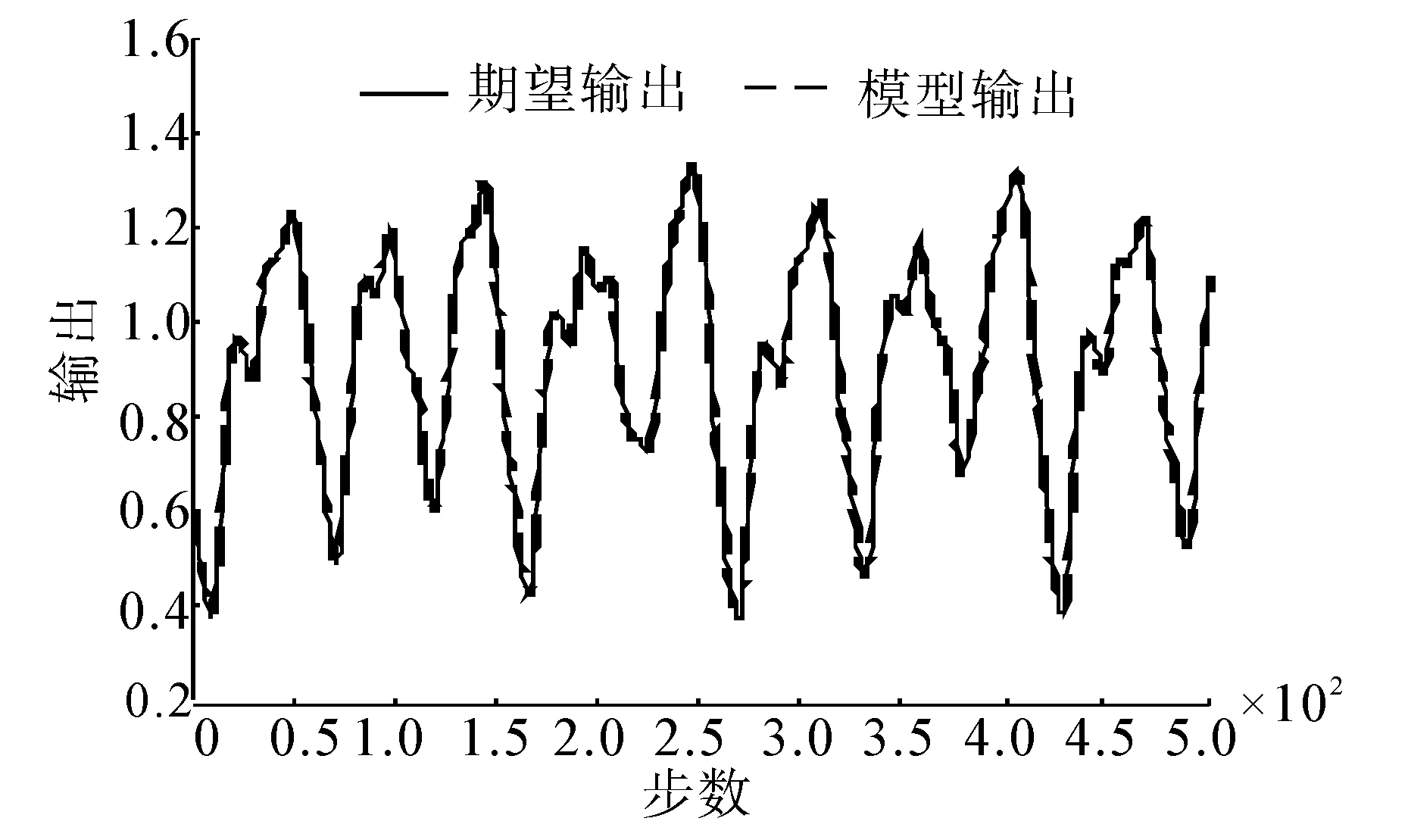
(a)建模逼近曲线

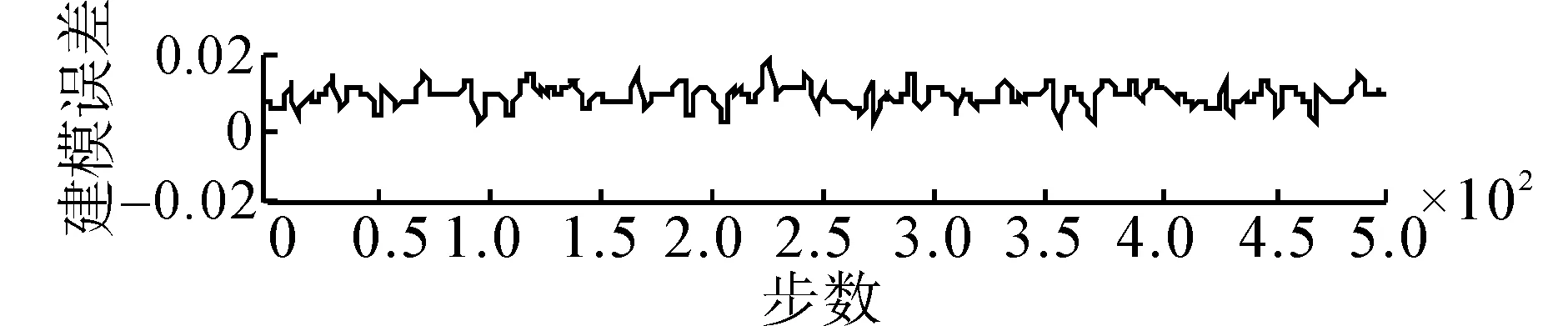
(b) 建模误差曲线图5 BFO-RLS 预测结果Fig.5 Prediction result of BFO-RLS

为了检验MFOA-LW建模的鲁棒性，在建模数据集中加入一定比例的例外点：随机选取per%的建模数据对，输入保持不变，输出加上[-15，15]的均匀分布的随机数。为了充分体现LW方法的鲁棒性，不断地增加例外点的比例(0～50%)。LW中，最大实验次数L_max=1 500，学习率η=0.09。为了表现本文方法的鲁棒性，仿真结果与MFOA-RLS方法进行比较。

表2给出了在建模数据集中加入不同比例的例外点时，2种方法的均方根误差，由于输入加入的是随机数，为了克服仿真结果的偶然性，每个结果均为20次仿真结果的平均值。

表2 含有不同比例例外点时，2种方法的预测误差(RMSE)

图3和图6分别为不包含例外点(0%)时RLS方法和LW方法的建模结果，图7和图8是含30%例外点时的建模结果。

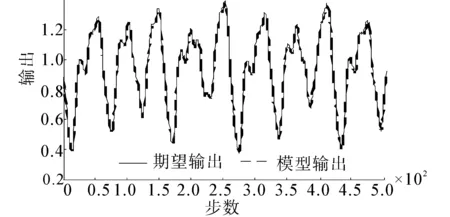
(a)建模曲线

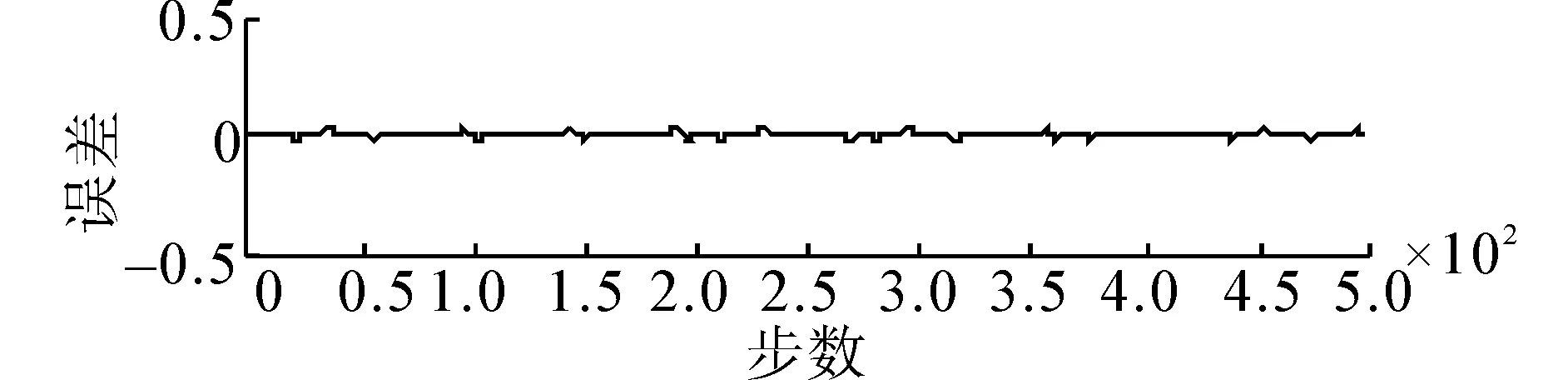
(b) 误差曲线图6 MFOA-LW方法的建模结果(无例外点) Fig.6 Modeling result of MOFA-LW (without outliers)

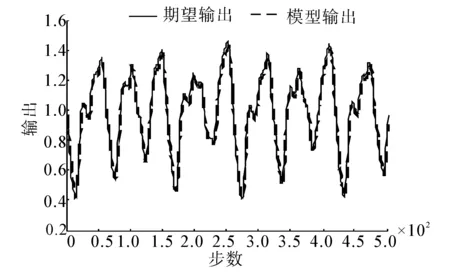
(a)建模曲线

(b) 误差曲线图7 MFOA-LW方法的建模结果(30%例外点)Fig.7 Modeling result of MOFA-LW (with 30% outliers)

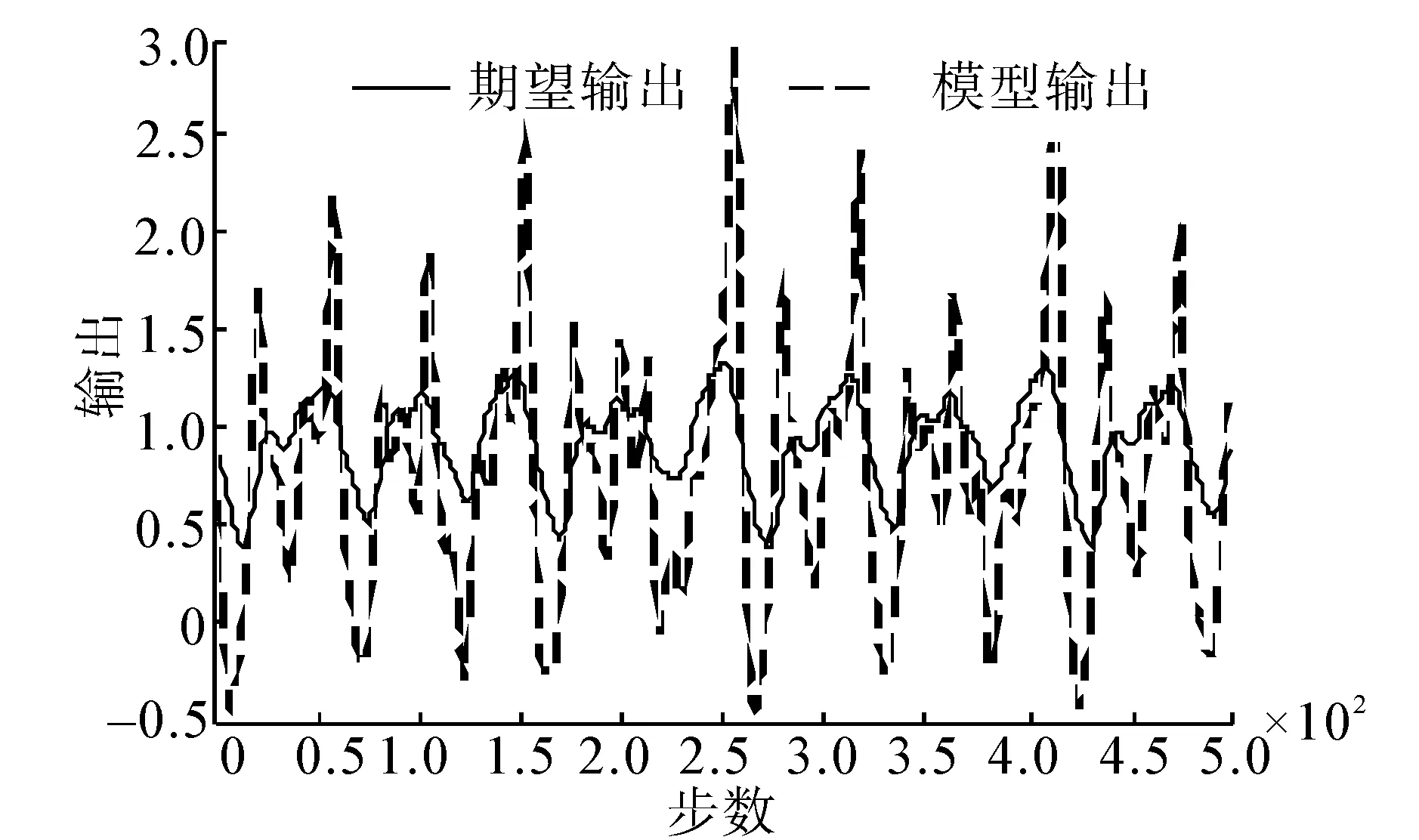
(a)建模曲线

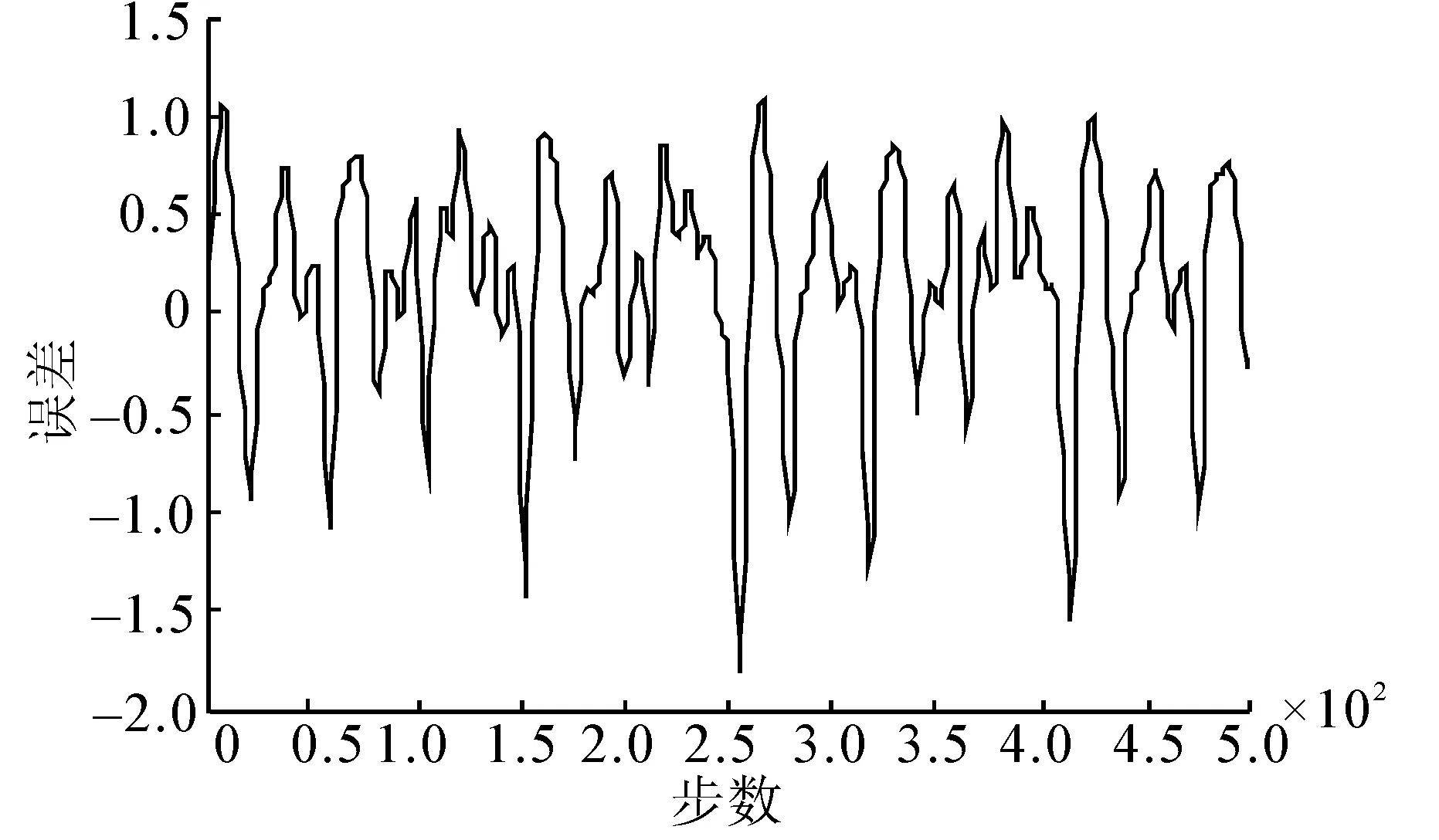
(b) 误差曲线图8 MFOA-RLS方法的建模结果(30%例外点)Fig.8 Modeling result of MOFA-RLS (with 30% outliers)

由以上的仿真结果可以看出，在含有例外点(10%～50%)时，MFOA-LW方法明显地对例外点有较强的鲁棒性，建模精度高出一个数量级，能较准确地建立混沌时间序列的模糊预测模型。

4 结束语

针对混沌时间序列预测问题，本文提出了一种基于MFOA-LW方法的鲁棒模糊预测算法。MFOA优化模型的前提参数，LW方法优化模型的结论参数，实现了模糊模型的全局优化。MFOA算法具有计算简单，容易编程，收敛速度快和成熟收敛等优点，应用在模糊模型辨识方面具有很大的优越性。最小Wilcoxon方法辨识模型具有鲁棒性，当训练数据中出现例外点时，LW方法仍然可以有效地辨识出模糊模型。为了检验所提方法的有效性，用本文方法对Mackey-Glass混沌时间序列进行了建模和预测，并与其他方法进行了比较。仿真结果表明，在系统不存在例外点时，采用MFOA-RLS方法的建模精度高于PSO-RLS、BFO-RLS等方法，这证明了MFOA的优越性；在系统存在例外点时，MFOA-LW方法辨识出的模型仍然具有较高的精度，可以满足辨识要求，但MFOA-RLS方法的辨识精度很低，根本无法有效地预测混沌时间序列，这充分验证了本文方法的鲁棒性，表明在存在例外点的情况下，这是一种有效的混沌时间序列预测方法，在复杂有干扰的非线性系统的研究中有较高的实用价值。

参考文献:

[1]毛剑琴,姚健,丁海山. 基于模糊树模型的混沌时间序列预测[J]. 物理学报, 2009, 58(4): 2220-2230.

MAO Jianqin, YAO Jian, DING Haishan. Chaotic time series prediction based on fuzzy tree[J]. Acta Physica Sinica, 2009, 58(4): 2220-2230.

[2]王宏伟,马广富. 基于模糊模型的混沌时间序列预测[J]. 物理学报, 2004, 53(10): 3293-3297.

WANG Hongwei, MA Guangfu. Prediction of chaotic time series based on fuzzy model[J]. Acta Physica Sinica, 2004, 53(10): 3293-3297.

[3]刘福才,张彦柳,陈超. 基于鲁棒模糊聚类的混沌时间序列预测[J].物理学报, 2008, 57(5): 2784-2790.

LIU Fucai, ZHANG Yyanliu, CHEN Chao. Prediction of chaotic time series based on robust fuzzy clustering[J]. Acta Physica Sinica, 2008, 57(5): 2784-2790.

[4]PAN W T. A new fruit fly optimization algorithm: taking the financial distress model as an example [J]. Knowledge-Based Systems, 2012, 26(2): 69-74.

[5]许智慧, 王福林, 孙丹丹, 等. 基于FOA-RBF神经网络的外贸出口预测[J]. 数学的实践与认识, 2012,42(13): 14-19.

XU Zhihui, WANG Fulin, SUN Dandan, et al. A forecast of export trades based on the FOA-RBF neural network[J]. Mathematics in Practice and Theory, 2012, 42(13): 14-19.

[6]潘文超. 应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估[J]. 太原理工大学学报:社会科学版, 2011, 29(4): 1-5.

PAN Wenchao. Using fruit fly optimization algorithm optimized general regression neural network to construct the operating performance of enterprises model[J]. Journal of Taiyuan University of Technology: Social Sciences Edition, 2011, 29(4): 1-5.

[7]王雪刚, 邹早建. 基于果蝇优化算法的船舶操纵响应模型的辨识[J]. 大连海事大学学报:自然科学版, 2012, 38(3): 1-4, 8.

WANG Xuegang, ZOU Zaojian. Identification of ship manoeuvring response model based on fruit fly optimization algorithm[J]. Journal of Dalian Maritime University: Natural Science Edition, 2012, 38(3): 1-4, 8.

[8]HOGG R V, MCKEAN J W, CRAIG A T. Introduction to mathematical statistics[M]. 6th ed. Englewood Cliffs, NJ: Prentice-Hall, 2005: 531-570.

[9]SUN T Y, TSAI S J, TSAI C H. Nonlinear function approximation based on least Wilcoxon Takagi-Sugeno fuzzy model[C]//The Eighth International Conference on Intelligent Systems Design and Applications. Kaohsiung, China, 2008: 312-317.

[10]MAJHI B, PANDA G. Robust identification of nonlinear complex systems using low complexity ANN and particle swarm optimization technique[J]. Expert Systems with Applications, 2010, 38(1): 321-333.

[11]NITHIN V G, PANDA G. A robust evolutionary feedforward active noise control system using Wilcoxon norm and particle swarm optimization algorithm[J]. Expert Systems with Applications, 2012, 39:7574-7580.

[12]TAKAGI T, SUGENO M. Fuzzy Identification of system and its application on modeling and control[J]. IEEE Trans on Systems, Man and Cybernetics, 1985, 15(1):116-132.

[13]LI C Q, XU S P, LI W, et al. A novel modified fly optimization algorithm for designing the self-tuning proportional integral derivative controller [J]. Journal of Convergence Information Technology, 2012, 7(16): 69-77.

[14]刘福才. 非线性系统的模糊模型辨识及其应用[M]. 北京:国防工业出版社, 2006: 41-44.

[15]MACKEY M C, GLASS L. Oscillation and chaos in physiological control systems[J]. Science, New Series, 1977, 197(4300): 287-289.