带有高斯扰动的混沌神经网络及应用

许楠, 刘桂阳 ,徐耀群

(1.黑龙江八一农垦大学 信息技术学院，黑龙江 大庆 163319； 2.哈尔滨商业大学 系统工程研究所，黑龙江 哈尔滨 150028)

制造混沌神经计算机一直是人们追求的目标，然而由于元器件的不稳定性，在一定情况下势必会出现微小扰动从而对网络模型产生影响，扰动的引入使得混沌神经网络具有更加复杂的动力学特性，同时对网络的应用产生一定影响，影响严重时会导致网络失稳，因此研究神经网络的抗扰动能力是有必要的。高斯函数是径向基函数[1]的一种，同其他径向基函数一样存在宽度参数，本文在Chen’s混沌神经网络基础上引入高斯函数扰动，对网络内部状态进行改进，分析了混沌神经元模型的动力学特性，以及宽度参数对扰动强弱的影响，在此基础上研究混沌神经网络的抗扰动能力，并在引入高斯函数扰动情况下，利用该网络解决旅行商最短路径(traveling salesman problem，TSP)问题，仿真结果表明，网络具有较高的抗扰动能力。

1 带高斯扰动的暂态混沌神经元模型

在Chen’s混沌神经网络模型基础上[2]，加入由高斯函数构成的扰动项，现将新模型的单个神经元模型描述如下：

x(t)=1/(1+exp(-y(t)/ε0))

(1)

y(t+1)=ky(t)-z(t)(x(t)-I0)+f(y(t))

(2)

z(t+1)=(1-β)z(t)

(3)

f(u)=exp(-u2/δ2)

(4)

式中：ε0是输出函数x(t)的陡度参数；神经元的激励函数x(t)选取Sigmoid函数；k为神经隔膜的阻尼因子，0≤k≤1；y(t)为神经元的内部状态，其t+1时刻状态受到t时刻状态影响；z(t)是自反馈连接项；f(u)为高斯函数，它用来作为内部函数扰动项；δ是径向基函数的扩展常数或称宽度；β是退火参数，其值对z(t)有着决定性影响；I0为一正参数。

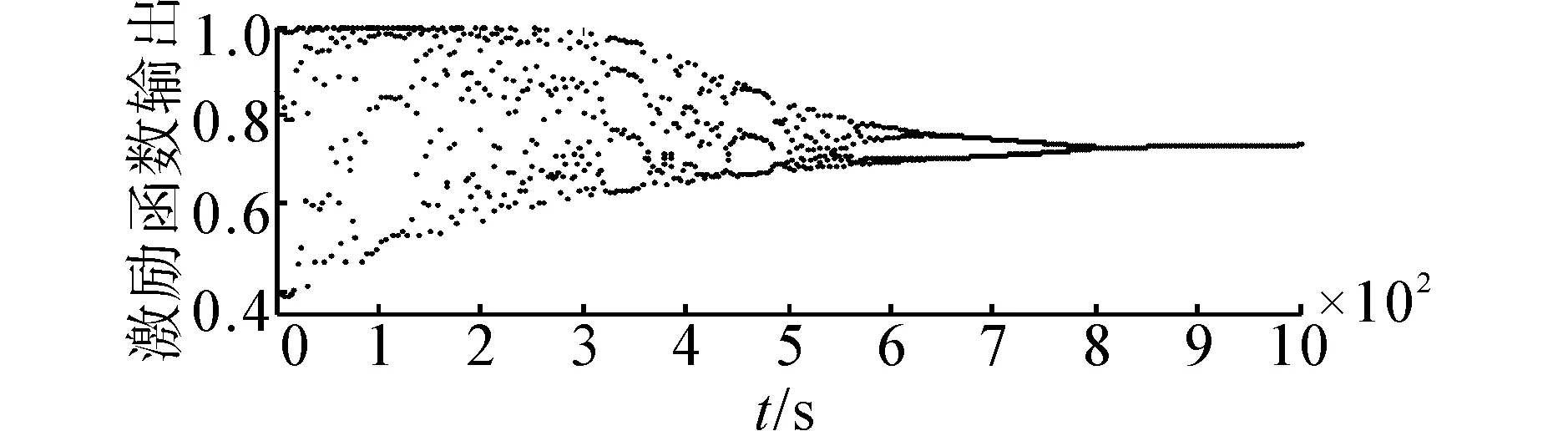
当参数选取ε0=0.1，y(1)=0.5，z(1)=0.5，k=0.9，I0=0.45，δ=0.05固定不变时，分别选取β=0.003与β=0.002 5时神经元的倒分岔图和最大Lyapunov指数时间演化图如图1、2所示。

(a)神经元倒分叉图

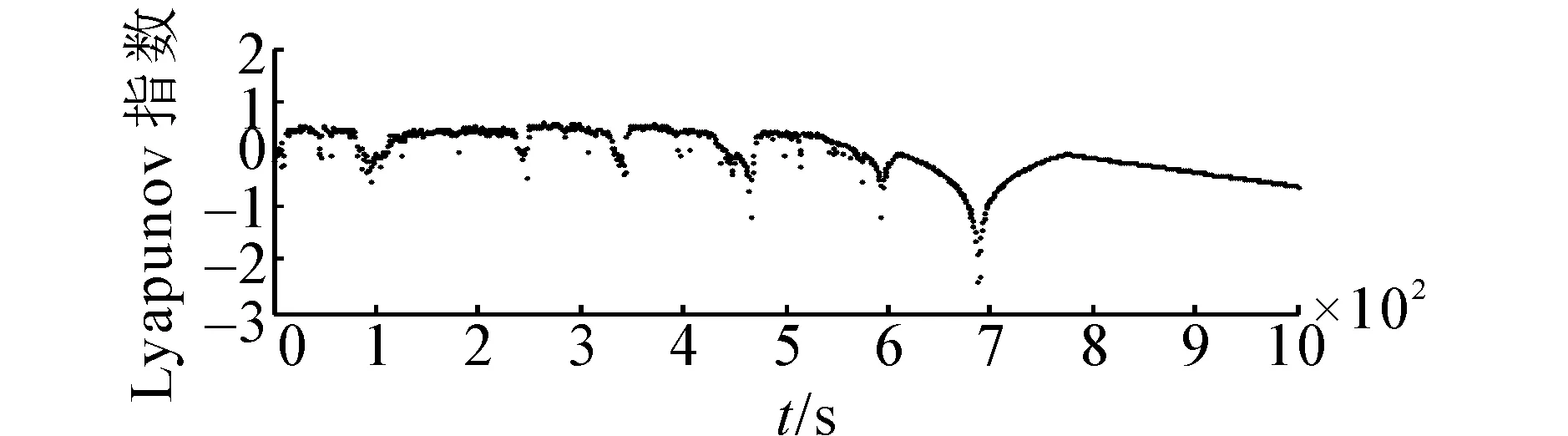
(b)最大Lyapunov指数时间图1 β=0.003时神经元倒分叉图与最大Lyapunov指数时间演化图Fig.1 State bifurcation and the time evolution of the maximal Lyapunov exponent of the neuron when β=0.003

(a)神经元倒分叉图

(b)最大Lyapunov指数时间图2 β=0.002 5时神经元倒分叉图与最大Lyapunov指数时间演化图Fig.2 State bifurcation and the time evolution of the maximal Lyapunov exponent of the neuron when β=0.002 5

由图1、2可知，加入了高斯扰动的混沌神经元具有暂态混沌动力学行为，网络的搜索及收敛快慢依赖于模拟退火参数β的值，β为0.003时收敛点在t为800处，β为0.002 5时收敛点在t为950处。由式(3)不难分析出：β越小，模拟退火温度[3]z(t)下一时刻较上一时刻变化越不明显，温度降低较慢，这就使得混沌搜索能够充分发挥作用，相对搜索时间较长，从而可以逃离局部极小点限制，找到全局最小点；β较大时，模拟退火温度z(t)下一时刻较上一时刻变化明显，温度较低、较快，这使得收敛速度得以加快，但若β过大，进入平衡点太过迅速，易使搜索陷入局部极小点，而不能求得全局最优解，因此应适当选取β值。

模拟退火参数β值对神经元模型的影响可以通过数学推理得出：β取值范围在0<β<1,通过式(3)不难看出z(t)是一个递减过程，递减速度由(1-β)控制，而(1-β)随着β值的增大而减小，也就是说，β值越大，z(t)递减得越快，β值越小，z(t)递减得越慢，相对的模拟退火温度冷却较缓慢。

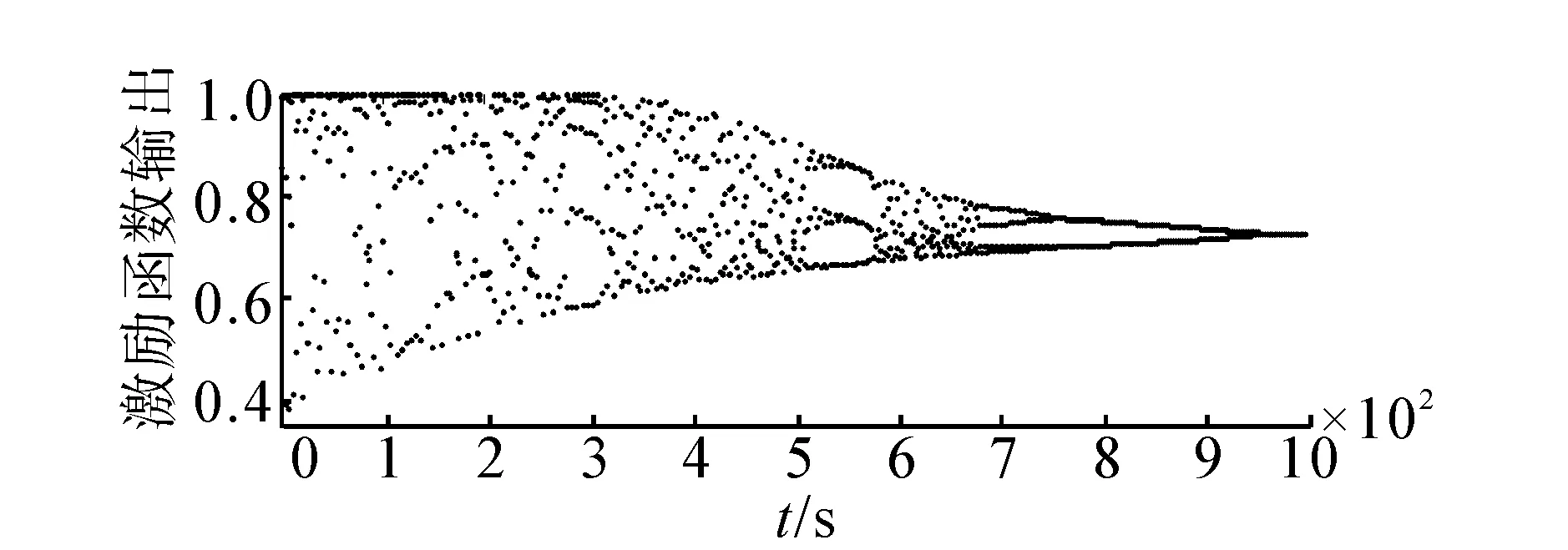
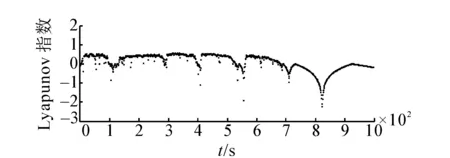
下面考查高斯函数的宽度参数δ对该神经元动力学特性的影响。当参数选取ε0=0.1，y(1)=0.5，z(1)=0.5，k=0.9，I0=0.45，β=0.003固定不变时，选取δ=0.07时神经元的倒分岔图和最大Lyapunov指数时间演化图如图3所示。

当β=0.003时，δ=0.05的倒分岔图和最大Lyapunov指数时间演化图与图3比较不难看出：δ=0.07混沌搜索进入稳定状态的位置是t为700左右，很明显比δ=0.05时稳定位置t为800左右搜索过程缩短，收敛点提前。说明δ越小加入到内部状态y(t)中的扰动就越大，从而影响了网络混沌搜索的随机性及轨道遍历性[4]，随机性可以保证大范围搜索能力，轨道遍历性使系统按自身的演化行为不重复地遍历所有可能状态，它具有使网络避免陷入局部极小的能力求解能力，因此δ取值应控制高斯函数所产生的扰动在一定范围内，才能使网络能够快速、有效的求解全局最小点。

(a)神经元倒分叉图

(b)最大Lyapunov指数时间图3 δ=0.07时神经元倒分叉图与最大Lyapunov指数时间演化图Fig.3 State bifurcation figure and the time evolution figure of the maximal Lyapunov exponent of the neuron when δ=0.07

由式(4)可以通过仿真试验做出如图4所示的高斯曲线。

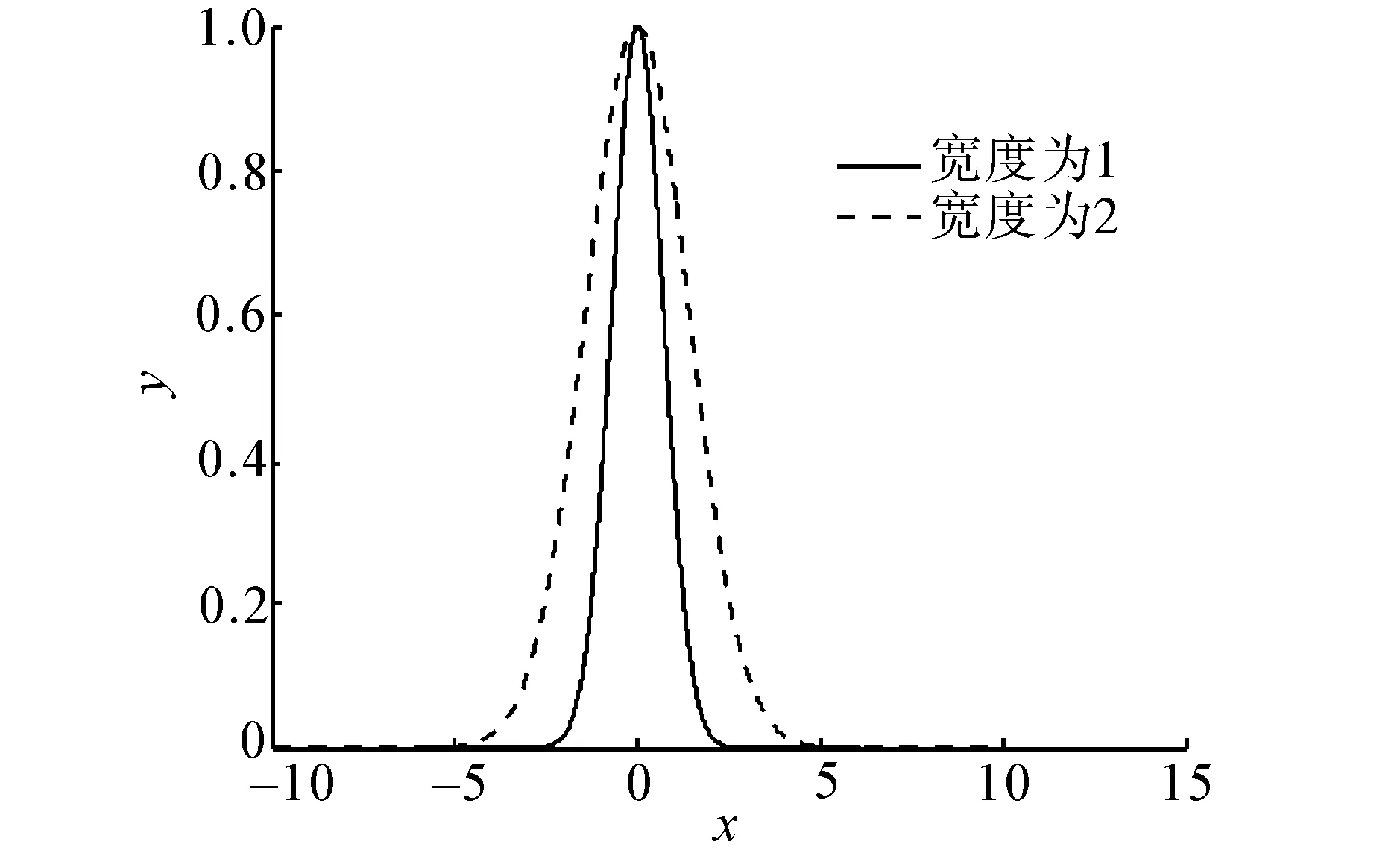
图4 δ=1与δ=2时的高斯曲线Fig.4 Gaussian function when δ=1 and δ=2

由该图可以看出：宽度越小，高斯曲线数值在0值两端变化越迅速，曲线较“陡峭”且趋向于垂直横轴；宽度越大，高斯曲线数值在0值两端变化缓慢，曲线较“平稳”，趋向于弧线。这说明对于径向基函数而言，宽度参数决定该函数的选择性，宽度越小，函数的选择性[5]越大，产生的扰动比较强烈；宽度越大，函数的选择性降低，所产生的扰动相对而言不是很大，对网络的求解能力影响减弱。

2 带高斯扰动的混沌神经网络模型

根据上述带有高斯扰动的混沌神经元模型，构造如下带有高斯函数扰动的暂态混沌神经网络模型：

x(t)=1/(1+exp(-y(t)/ε0))

(5)

yi(t+1)=kyi(t)+f(y(t))+

(6)

zi(t+1)=(1-β)zi(t)

(7)

f(u)=exp(-u2/δ2)

(8)

网络模型中i=1,2,…,n；xi(t)是由Sigmoid函数构成的激励函数；yi(t)为内部状态；k为神经隔膜的阻尼因子，0≤k≤1，表示网络记忆保留或遗忘内部状态的能力，其值越接近1越表明下一时刻内部状态变化不大，保留能力较强，其值越接近0表明下一时刻内部状态有很大变动，遗忘能力较强；zi(t)自反馈连接项，其值是不断减小的，当减小到趋近0值时，网络将结束混沌搜索状态，进入稳定平衡状态；β是模拟退火参数；wij为从神经元j到神经元i的连接权值，且wij=wji，wii=0；Ii为神经元i的输入偏差；γ为输入的正的尺度参数，代表着能量函数对动态特性的影响，γ过大则能量函数影响太强，有可能无法得到暂态混沌现象，γ过小则能量函数影响太弱，有可能无法收敛到最优解；I0为一正参数；f(u)为高斯函数，其中δ为宽度参数。

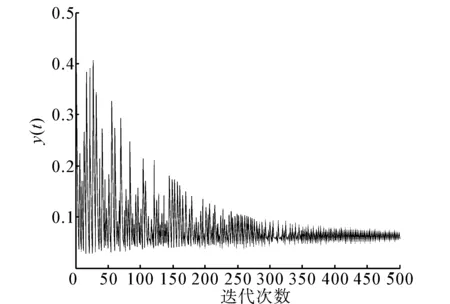
图5 δ=0.03时内部状态y(t)随迭代次数的变化曲线Fig.5 The curve for the change of y(t) when δ=0.03

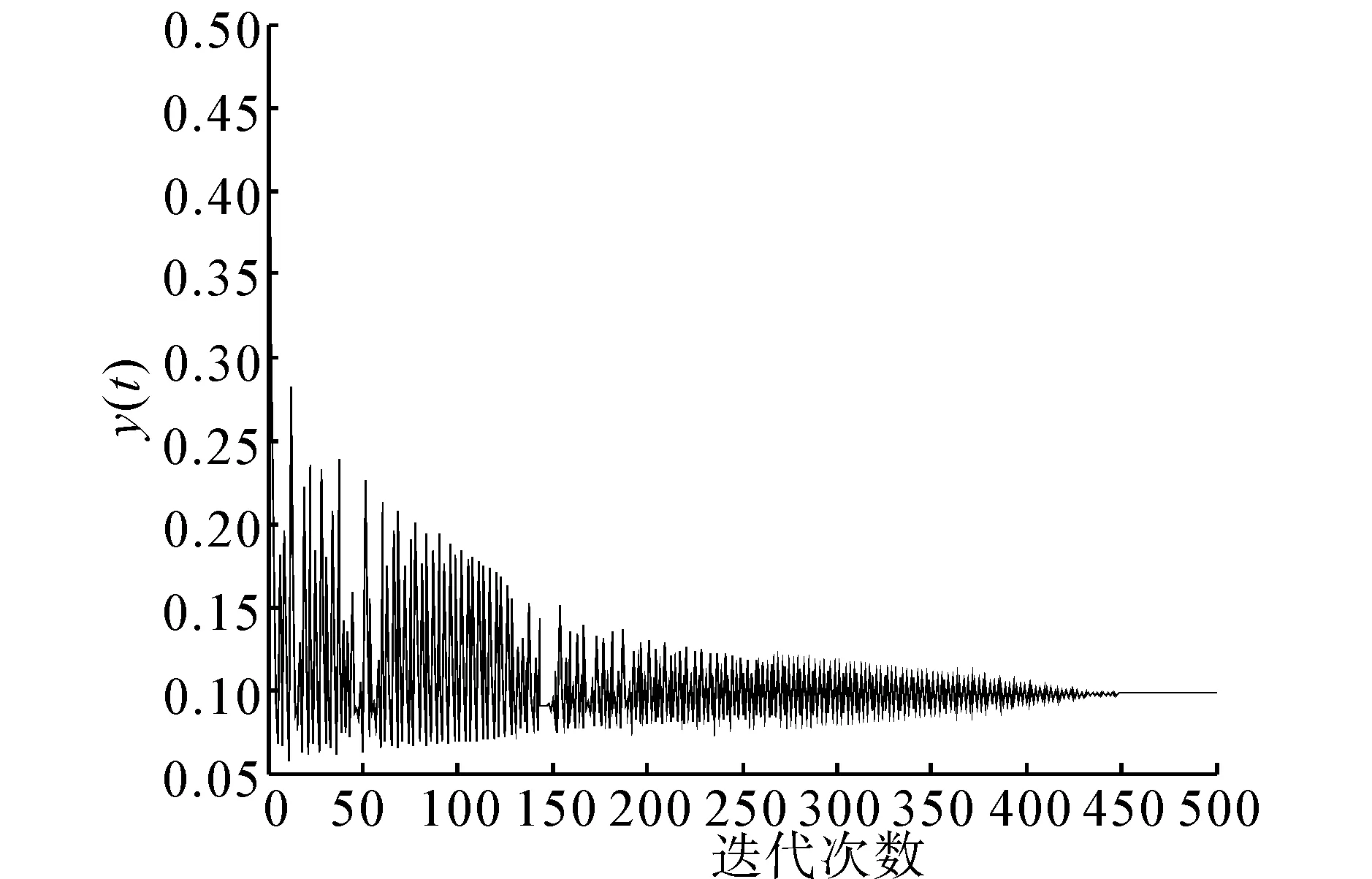
图6 δ=0.05时内部状态y(t)随迭代次数的变化曲线Fig.6 The curve for the change of y(t) when δ=0.05

随着时间t的推移，y(t)变化幅度越来越小，δ为0.03时，y(t)稳定在0.06附近，而δ为0.05时，y(t)稳定在0.1附近，不妨通过式(8)对此进行数学推导，δ越小，u2/δ2越大，exp(u2/δ2)越大，但是exp(-u2/δ2)却反而越小，因此，δ越小，扰动项f(u)对内部状态改变会增强，而随着时间的推移，内部状态会稳定在较低值，由此，更能理解上述结果。

3 解决旅行商最短路径问题(TSP)

旅行商最短路径问题(TSP)[7]可描述为：给定n个城市以及每2个城市之间的距离，若要使旅行商经过每个城市且各城市仅经过一次，求最短路线。

所求最短路径并满足TSP问题约束条件的一个能量函数如式(9)描述。

(9)

式中：Vxi为神经元输出，代表第x个城市在第i次序上被访问，dxy为城市x、y之间的距离。由于行列式的对称性，系数A=B，一个全局最小的E值代表一条最短的有效路径。本文采用以下经典归一化后的10个城市坐标：(0.4, 0.443 9); (0.243 9, 0.146 3); (0.170 7, 0.229 3); (0.229 3, 0.71 6); (0.517 1,0.941 4); (0.873 2, 0.653 6); (0.687 8, 0.521 9); (0.848 8, 0.360 9); (0.668 3, 0.253 6); (0.619 5, 0.263 4)。该10城市最短路径为2.677 6，路径如图7。

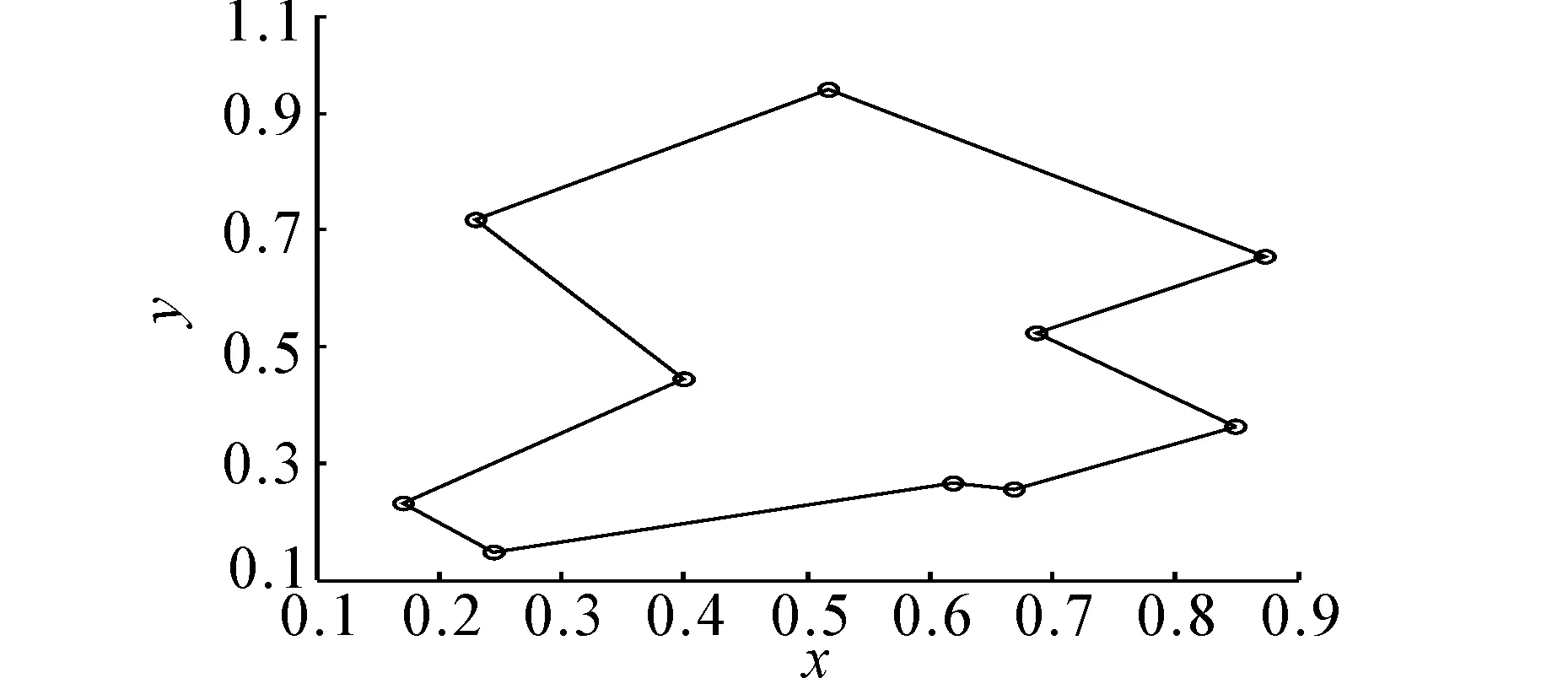
图7 10个城市TSP问题的最优解Fig.7 The optimal distance of 10 city TSP

当取ε0=0.2，z(1)=0.5，k=0.88，I0=0.9，β=0.3，A=2，D=5，γ=0.6固定不变时，分别选取不同的宽度参数δ值，研究其对TSP求解的影响，表1是该情况下200次随机分配初始值的仿真数据结果。

表1 在不同δ值条件下200次随机分配初始值的试验数据

由表1可以看出： 当宽度参数δ的值在[0.676,0.710]时网络的合法路径比例均为100%，最优路径比例均在85%以上，说明δ若在此区间取值，扰动不是很强烈，不会对网络的寻优能力造成很大影响；但随着δ取值的不断减小，网络的合法路径以及最优路径比例均有所下降，说明随着δ的减小，高斯函数产生的扰动越来越强烈，使网络不能很好地利用混沌的全局遍历特性，致使求解能力下降，尤其当δ取值小于0.664时，合法路径与最优路径比例下降迅速，因此，网络的抗扰动能力随着宽度值的减小而变弱。

除了径向基函数的宽度参数外，神经隔膜阻尼因子[8]k对网络的寻优能力也有很大影响，当取ε0=0.2，z(1)=0.5，δ=0.7，I0=0.9，β=0.3，A=2，D=5，γ=0.6固定不变时，分别选取不同的k值，研究其对TSP求解的影响，表2是该情况下200次随机分配初始值的仿真数据结果。可以看出，在δ及其他参数固定情况下，高斯函数形成的扰动作用于网络，此时的网络具有一定的抗干扰能力，但也较敏感依赖于神经隔膜阻尼因子的取值，当k值在[0.876,0.882]范围内时，网络的合法路径比例为100%，最优路径比例均在80%以上，但随着k值的减小，合法路径及最优路径比例均明显下降，说明该网络在内部状态记忆能力较强时，可以逃离极小点限制，而在内部状态遗忘能力较强时，网络求解组合优化问题的能力大大降低，网络不易求得全局最优解。

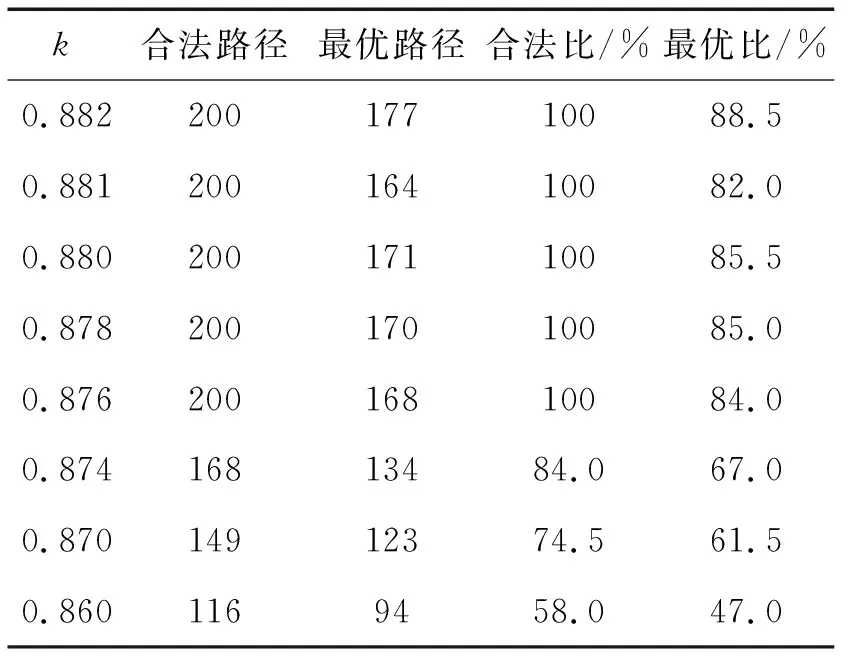
表2 在不同k值情况下200次随机分配初始值的试验数据

由表2上述仿真实验结果，受到网络模型各个参数的制约，某一参数改变会影响全局结果，这也是混沌神经网络的特性之一，即敏感依赖于网络参数初值，因此上述结果是在其他参数值固定不变的情况下得出的优化性能情况，并不具备普遍性，特在此说明。

4 结束语

本文将高斯扰动加入混沌神经网络的内部状态中，通过神经元倒分岔图以及Lyapunov指数演化图，分析了其混沌动力学行为，说明了高斯函数的宽度参数对混沌行为的影响。在带有高斯扰动的神经元模型基础上构建混沌神经网络模型，通过简化能量函数，模拟分析了内部状态随着迭代次数的变化情况，说明了宽度参数值越小，对网络的扰动就会越强烈。将该网络模型应用于求解TSP问题，通过仿真试验可知，网络具有较强的抗扰动能力，选取适当参数值，且扰动不是很强烈的情况下，仍然能以85%以上的最优路径比例求得全局最优解。

参考文献:

[1]黄永聪，张旭，吴义纯，等. 改进的径向基函数网络的研究及应用[J]. 计算机技术与发展， 2010， 20(5): 164-167.

HUANG Yongcong, ZHANG Xu, WU Yichun, et al. Research and application of improved genetic algorithm- based RBFANN[J]. Computer Technology and Development，2010， 20(5): 164-167.

[2]CHEN L, AIHARA K. Chaotic simulated annealing by a neural network model with transient chaos[J]. Neural Networks, 1995, 8(6): 915-930.

[3]张慧，刘湘南，黄刚. 基于模拟退火遗传算法的GMDH网络模型[J]. 华中师范大学学报：自然科学版， 2013， 47(2): 24-28.

ZHANG Hui，LIU Xiangnan，HUANG Gang. The GMDH network model based on simulated annealing and genetic algorithm[J]. Journal of Huazhong Normal University: Natural Sciences Edition, 2013, 47(2): 24-28.

[4]HOPFIELD J. Neural networks and physical systems with emergent collective computational abilities[C]//Proceedings of the National Academy of Sciences. [S.l.], 1982, 79: 2554-2558.

[5]许楠，刘丽杰. 径向基函数混沌神经元系统及其应用[J].计算机工程与应用，2014, 50(4): 73-76.

XU Nan， LIU Lijie. RBF chaotic neuron system and its application[J]. Compter Engineering and Application, 2014， 50(4)： 73-76.

[6]徐耀群，何少平，张莉. 带扰动的混沌神经网络研究[J]. 计算机工程与应用， 2008, 44(36)： 66-69.

XU Yaoqun， HE Shaoping， ZHANG Li. Research on chaotic neural network with disturbance[J]. Compter Engineering and Application， 2008， 44(36)： 66-69.

[7]代桂平，王勇，侯亚荣. 基于遗传算法的TSP问题求解算法及其系统[J]. 微计算机信息， 2010， 26(4): 15-17.

DAI Guiping， WANG Yong， HOU Yarong. A TSP solving algorithm and system based on genetic algorithm[J]. Microcomputer Information， 2010， 26(4): 15-17.

[8]徐耀群，杨雪玲. 一类具有反三角函数自反馈的混沌神经网络及其应用[J]. 哈尔滨商业大学学报：自然科学版， 2010(3)： 72-76.

XU Yaoqun，YANG Xueling. A class of chaotic neural networks with anti-trigonometric function self-feedback and its application[J]. Journal of Harbin University of Commerce: Natural Sciences Edition，2010，6(3)： 72-76.