基于二进制区分矩阵的离散化算法

侯利娟，史长琼

长沙理工大学计算机与通信工程学院，长沙 410004

基于二进制区分矩阵的离散化算法

侯利娟，史长琼

长沙理工大学计算机与通信工程学院，长沙 410004

提出离散化中基本二进制区分矩阵的定义及其简化方法和基于简化二进制区分矩阵的离散化算法，把符号运算转变成二进制运算，有效地节约了存储空间和运算时间。从区分度和区分率两个不同层次考察断点的重要性，引导求解过程趋于最优化，只采用新增加的断点对应位与矩阵的行相应位进行运算，进一步提高计算效率。实例分析表明算法是正确有效的。

粗糙集理论；离散化；二进制区分矩阵；简化二进制区分矩阵

1 引言

数据离散化是粗糙集理论中的预处理问题之一，处理结果的好坏，直接影响到属性约简和值约简，人们对基于粗糙集模型的离散化方法已经取得了一些有价值的研究成果。Nguyen等人提出了粗糙集与布尔逻辑方法[1]，该方法具有完备性，即理论上可以找出所有可能组合的离散化断点集，但是其算法复杂度是指数级的，无法在实际问题中应用，离散化问题都是在此基础上提出的启发式算法。文献[2]提出的贪心算法，是基于断点对实例的可分性，属于局部寻优搜索算法，算法时间复杂度和空间复杂度较高，更适合小样本数据集；文献[3-4]提出的基于属性重要性的算法，优先选取重要性高的属性上的断点。用判别函数对候选断点进行筛选是一类较常用的离散化算法，文献[5-8]给出了基于信息熵的离散化算法，该算法用信息熵作判断标准，从候选断点中选择合适的断点，然后删除一些冗余的断点来优化离散结果；文献[9]提出改进粒子群优化的离散算法；文献[10]提出一种新的区间拆分方法；文献[11]提出了连续属性决策表信息系统的图论形式和离散化的图论方法；文献[12]提出了一种基于密度分布函数聚类的连续属性离散化算法。根据基于聚类思想的离散化算法是否考虑连续属性的互补性和相关性；文献[13]将算法分为整体属性离散化算法和单个属性离散化算法；文献[14]提出一种基于超立方体聚类的连续属性整体离散化算法；文献[15]提出基于传统区分矩阵的数据离散化算法，把所有候选断点集中到区分矩阵中，以断点核为起点，根据候选断点在区分矩阵中出现的频率作为启发信息，逐次选择最重要的断点加入到断点子集中。

最小断点集的计算问题是一个NP问题[1]，论域规模的增加和属性值的组合爆炸对各种算法的效率影响很大。文献[15]用断点集合表示矩阵元素，消耗了大量的存储空间，且所生成的区分矩阵在求解时，需要大量的符号逻辑运算。本文提出了基本二进制区分矩阵的定义及其简化方法和在简化二进制区分矩阵基础上的离散化算法，和文献[15]相比可以有效地减少矩阵的存储空间，在矩阵运算上，采用二进制的与运算代替符号运算，可以有效地节约运算时间。

2 离散化问题的描述

3 基本二进制区分矩阵

3.1 基本二进制区分矩阵的定义

文献[15]中传统区分矩阵的元素是断点的集合，消耗了大量的存储空间，可以把它转换成基本二进制区分矩阵，用二进制元素代替符号集合，节约存储空间，基本二进制区分矩阵的定义如下：

定义1基本二进制区分矩阵BM构造如下：

3.2 基本二进制区分矩阵的分析

基本二进制区分矩阵有下面四种主要的形式：

（1）如果某一列中所有的元素都为1，则这列所对应的断点能区分由所有断点区分的所有实例对，这个断点是决策表的一个最小断点集，这种情况非常少见。

（2）如果某一列中所有的元素都为0，则这列所对应的断点不能区分任何一个实例对，因此，它是不必要的。

（3）如果某一行中元素1的个数为1，则元素1所对应的断点是能区分这个实例对的唯一断点，因此，它是必要的，把这样的断点称为断点核。

（4）某一列中元素1所占的比例越大，相应断点能区分的实例对个数就越多，断点的重要程度就越大。

4 简化二进制区分矩阵SBM

基本的二进制区分矩阵将传统区分矩阵中的元素用二进制整数表示，其所占存储空间比用符号表示的矩阵要少，另外，在由区分矩阵计算最小断点集时，将符号逻辑运算转换成了位逻辑运算，从而提高了效率。

但基本二进制区分矩阵中还存在着大量的重复信息，仍占用比较大的存储空间，根据符号逻辑运算中的吸收律，设计了一个算法用于形成简化的二进制区分矩阵，简化算法如下：

5 基于简化二进制区分矩阵的离散化算法

5.1 最小断点集的二进制表示

5.2 算法的核心思想

假设SBM(i，j)m是简化二进制区分矩阵的第m行，相应的实例对为(xi，xj)，CBmin中值为1的位和SBM(i，j)m中的相应位与运算的结果如果全为0，则(xi，xj)将不能被Cmin区分。基于这种思想，设计一种直观的算法，首先，选择一个CBmin，然后将CBmin中值为1的位与SBM的每一行相应位进行与运算，如果所有行运算结果的每一位都为0，则重新选择CBmin，否则保留CBmin中的值为1的位，重复这个过程直到遍历了所有的行，最终所得的CBmin就是一个最小断点集的二进制表示。

算法的关键就是如何选择CBmin，即选择哪些断点。为了衡量每个断点的重要性，给出了两个定义——断点的区分度和区分率，用它们来衡量断点的重要性，从而引导断点的选取。

根据这两个定义，选择断点时，可以优先选择重要性大的断点，避免盲目选择。

5.3 算法步骤

6 实例分析

表1 未离散化的决策表

表2 表1的基本二进制区分矩阵BM

根据二进制区分矩阵的简化方法可以得到表1的简化二进制区分矩阵如表3，和基本的二进制区分矩阵相比，矩阵元素进一步减少。

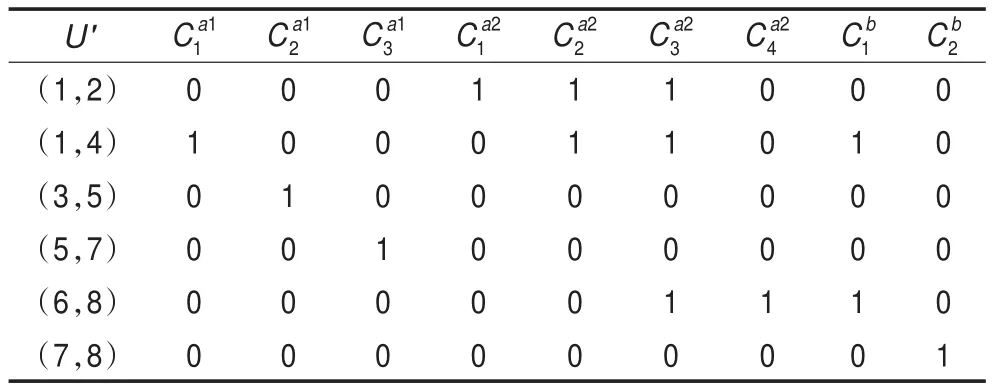
表3 表1的简化二进制区分矩阵

7 算法分析与比较

文献[15]用断点集合表示矩阵元素，由于矩阵是对称矩阵，只需要存储下三角矩阵即可，假设决策表有n个实例，所有条件属性共有m个候选断点，则文献[15]的步骤2中存储断点信息所需要的最大存储空间为n× (n-1)×m×2k比特（k为一整数，具体的值和开发平台有关，如C语言中k为8）。用本文中提出的基本二进制区分矩阵存储断点信息，最大需要存储空间为n×(n-1)×m比特，若用简化的二进制区分矩阵存储，存储空间将会进一步减少，但简化的二进制区分矩阵的规模和决策表的数据相关，最坏情况下需要的存储空间为n×(n-1)×m比特，是文献[15]的1/（2k），节约了较多的存储空间。

文献[15]主要的时间开销是步骤5中计算频率最高的断点，其基本操作是字符串的比较，每得到一个频率最高的断点最坏需要进行n×(n-1)×m×β次字符串的比较（0＜β≤1，当决策表不存在断点核时β=1）。本文5.3节中步骤5遍历简化二进制区分矩阵得到一个频率最高的断点需要的二进制与运算的次数最坏的情况为n×(n-1)×β次，节约了较多的运算时间。

8 结束语

本文提出离散化中基本二进制区分矩阵的定义及其简化方法和基于简化二进制区分矩阵的离散化算法，用二进制形式矩阵来代替传统矩阵表示对象之间的不可区分关系，把符号运算转变成二进制运算，有效地节约了存储空间和运算时间。通过对二进制区分矩阵的特点进行分析，定义了区分度和区分率两个概念，从不同层次考察断点的重要性，引导离散化过程趋于最优化。在矩阵的行和断点的二进制位与运算时，采用新增的断点对应的位和矩阵中行的相应位进行与运算，进一步节约运算时间，对大数据量的决策表的离散化具有重要的意义。下一步的工作可以用并行程序设计的方法设计在简化二进制矩阵过程中涉及到的两个二进制串的与运算。

[1]Nguyen H S，Skowron A.Quantization of real values attributes，rough set and Boolean reasoning approaches[C]// Proc of the 2nd Joint Annual Conference on Information Science.Wrightsville Beach：[s.n.]，1995：34-37.

[2]Nguyen S H，Nguyen H S.Some efficient algorithms for rough set methods[C]//Proc of Conference on Information Processing and Management of Uncertainty in Knowledge-based Systems，1996.

[3]侯利娟，王国胤.粗糙集理论中的离散化问题[J].计算机科学，2000，27（12）：89-94.

[4]王国胤.Rough集理论与知识获取[M].西安：西安交通大学出版社，2001.

[5]谢宏，程浩忠，牛东晓.基于信息熵的粗糙集连续属性离散化算法[J].计算机学报，2005，28（9）：1570-1574.

[6]白根柱，裴志利.基于粗糙集理论和信息熵的属性离散化方法[J].计算机应用研究，2008，25（6）：1701-1703.

[7]高建国，崔业勤.基于信息熵理论的连续属性离散化方法[J].微电子学与计算机，2011，28（7）：187-189.

[8]岳海亮，闫德勤.一种基于信息论的决策表连续属性离散化算法[J].计算机科学，2010，37（4）：231-233.

[9]汪凌，胡培.基于改进粒子群优化的粗糙集连续属性离散化[J].计算机工程与应用，2010，46（15）：115-117.

[10]李慧，闫德勤.一种基于粗糙集理论的连续属性离散化新算法[J].计算机应用研究，2010，27（1）：77-78.

[11]卢鹏，王锡淮.连续属性决策表离散化的图论方法[J].计算机工程与应用，2012，48（6）：13-16.

[12]李兴生，李德毅.一种基于密度分布函数聚类的属性离散化方法[J].系统仿真学报，2003，15（6）：804-806.

[13]苗夺谦.Routgh Set理论中连续属性的离散化方法[J].自动化学报，2001，27（3）：296-302.

[14]于金龙，李晓红，孙立新.连续属性的整体离散化[J].哈尔滨工业大学学报，2000，32（3）：48-53.

[15]秦川，黄欢.基于区分矩阵的数据离散化算法[J].计算机工程与应用，2008，44（35）：148-150.

HOU Lijuan,SHI Changqiong

School of Computer and Communication Engineering,Changsha University of Science and Technology,Changsha 410004,China

This paper puts forward the definition of the basic binary discernibility matrix and it’s simplify method in discretization.Discretization algorithm based on simplify binary discernibility matrix is proposed.It changes symbolic computation into binary operation,can save the storage space and computing time efficiently.Cut significance is investigated at two different levels,which can lead the solution to optimization.Only using the new adding cut’s corresponding bit operate with the rows of the matrix corresponding bit,can reduce computing time further.Analysis of the example shows that the algorithm is correct and efficient.

rough set theory;discretization;binary discernibility matrix;simplify binary discernibility matrix

A

TP18

10.3778/j.issn.1002-8331.1212-0373

HOU Lijuan,SHI Changqiong.Discretization algorithm based on binary discernibility matrix.Computer Engineering and Applications,2014,50（21）：214-217.

湖南省教育厅资助科研项目（No.09C083）。

侯利娟（1973—），女，讲师，研究领域为粗糙集理论与应用，数据挖掘等；史长琼（1968—），女，副教授，研究领域为计算机网络，数据挖掘等。E-mail：hlj1215@163.com

2013-01-04

2013-03-06

1002-8331（2014）21-0214-04

CNKI出版日期：2013-03-21，http://www.cnki.net/kcms/detail/11.2127.TP.20130321.0939.006.html