图像多尺度配准的小波域SURF算法

卫建龙，田铮，2，延伟东，范明

1.西北工业大学理学院，西安 710129

2.中国科学院遥感应用研究所遥感科学国家重点实验室，北京 100101

图像多尺度配准的小波域SURF算法

卫建龙1，田铮1，2，延伟东1，范明1

1.西北工业大学理学院，西安 710129

2.中国科学院遥感应用研究所遥感科学国家重点实验室，北京 100101

针对SURF描述子仅利用特征点的局部邻域信息而对于局部场景发生变化的图像容易产生误匹配的现象，提出了图像多尺度配准的小波域SURF算法。该方法对图像进行小波分解，利用低分辨率上得到的变换参数剔除高分辨率上的错误匹配，得到精确匹配点对，对图像进行配准。实验结果表明，该方法能有效地剔除误匹配点，提高图像配准的精度。

图像配准；加速稳健特征（SURF）；小波域；多尺度

1 引言

常用的描述子包括：不变矩描述子[4]、Fourier描述子[5]、线特征描述子[6]、SIFT描述子[7]、PCA-SIFT描述子[8]、GLOH描述子[9]、ICA-SIFT描述子[10]、SURF描述子[11]等。其中Lowe提出的SIFT局部特征描述子对于图像的平移、尺度、旋转及一定的视角变化都具有良好的不变性，因此被广泛应用于图像配准领域。但是SIFT算法明显的缺点是计算量大，时间复杂度很高，导致对SIFT特征提取和匹配所消耗的时间很长。因此Bay等人基于SIFT提出了SURF描述子，SURF与SIFT描述子类似，也具有对尺度和旋转的稳健性，并且在大大降低时间复杂度的基础上也能保证特征点的提取质量。Luo Juan等人用实验证明了由于SURF算法采用了积分图像、DoH近似及降低特征描述向量的维数使得SURF算法与SIFT相比在速度上有明显优势[12]，但是其匹配正确率却并不高，存在误匹配。

图像多尺度配准的特点是在图像的不同尺度上提取特征并建立特征间的对应关系。而小波变换良好的时频分析特性，使得小波域多尺度方法得到了较广泛的应用。Gang Hong介绍了一种基于小波的高分辨率遥感图像的配准方法[13]。在特征点检测阶段，利用小波的多分辨率的性质由细到粗产生金字塔图像来表示参考图像和待配准图像，通过寻找小波系数能量的局部最大值可以得到很多显著的特征点；在特征点匹配阶段，首先利用规范化的互相关方法初始化特征点之间的匹配关系，然后利用概率松弛方法剔除误匹配。

由于大多数的基于小波多尺度的图像配准方法都没有综合利用不同尺度上得到的变换参数，因此本文基于SURF描述子研究了图像多尺度配准的小波域SURF算法，综合利用了不同尺度上的特征匹配信息，以减少误匹配对数，提高正确匹配率。通过在光学遥感图像及SAR图像上的应用，验证了本文方法在剔除误匹配方面的有效性和可行性。

2 SURF算法

2008年Bay等人提出了SURF描述子，SURF算法整体流程与SIFT类似，但在每个步骤中采用了与SIFT不同的方法。SURF算法主要包含下面四个步骤：

（1）特征检测：特征检测方法也是基于尺度空间理论。Bay等人将Hessian矩阵中Gauss二阶微分与图像的卷积转化为盒子滤波运算，并用积分图像来加速卷积以提高计算速度，用Hessian矩阵求出极值后，在3×3×3的立体邻域内进行3D非最大值抑制，找到候选特征点，然后在尺度空间和位置空间进行插值运算，得到稳定的特征点位置及其尺度值。

（2）主方向确定：为了得到主方向值，Bay设计了一个以特征点为中心，张角为π/3的扇形滑动窗口，以步长0.2 rad左右，旋转滑动窗口，并对滑动窗口内图像Haar小波响应值dx、dy进行累加，主方向为最大Haar响应累加值所对应的方向，对得到的特征点逐个进行计算，可得每一个特征点的主方向。

（3）特征描述向量的生成：以特征点为中心，沿主方向将20 s×20 s的图像划分为4×4个子块。利用尺寸为2 s的Haar小波对每个子窗口图像进行响应值计算，分别得到沿主方向的响应值dy和垂直于主方向的响应值dx。然后以特征点为中心，对dy和dx进行Gauss加权计算，其中σ=3.3 s。最后分别对每个子块的响应值进行统计，得到每个子块的向量：

事实上，作者对自身事迹的书写，首先是对人们坚持追求幸福的有力呼吁，其次也是对时代变化的反映。易卜生的“娜拉”后，是因为千千万万个“娜拉”在中国出现，这才推翻了媒妁之言父母之命；同样的，也是因为千千万万个像“我”一般大胆追求幸福的新女性之存在，这才推动近代婚恋观念彻底向现代化方向蜕变。可以断言，张雅文女士所要写的，不仅仅是某一个体幸福，更是时代的幸福。

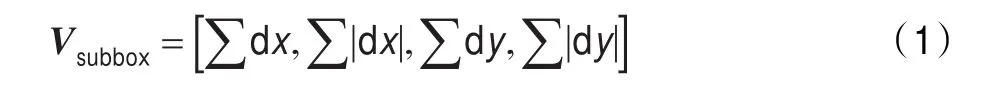
由于共有4×4个子块，SURF特征描述子共由4×4× 4=64维特征向量组成，再对向量进行归一化，从而使其对光照也具有一定的稳健性。

（4）特征匹配：从两幅图像中检测出特征点并得到64维的SURF描述子后，此时采用最近距离与次近距离之比作为特征点间的相似性度量，设定阈值，小于这个阈值的被认为是匹配点对。当然可以通过降低阈值的方式来增加SURF特征匹配的稳定性，但应注意，若阈值很小，那么匹配对数会很少，影响配准效果。

对于局部场景发生变化的图像，如地震前后或者包含噪声的图像，SURF算法在进行特征匹配时，也会产生误匹配，为了提高正确匹配率，本文提出了图像多尺度配准的小波域SURF算法。

3 图像多尺度配准的小波域SURF算法

在对SURF特征进行匹配时通过调节阈值参数可以获得大量的匹配点对，但是由于SURF本身就是一种特征描述子，它仅利用了特征点的局部信息，忽略了全局信息，对于具有特殊成像机理的图像而言（例如SAR图像），由于受到斑点噪声和局部场景变化的影响，会产生一定数目的误匹配，针对这个问题，本文研究了图像多尺度配准的小波域SURF算法。小波变换可将图像逐层分解为低频和高频部分，低频部分包含图像的整体结构信息，高频部分包含图像的局部细节信息。经过小波变换后的低分辨率图像受图像局部细节影响大大降低，这也使得在该尺度上提取的SURF特征更加稳健。利用在低分辨率下获得的变换参数作为初始变换参数，然后利用这些初始值指导高分辨率下的特征匹配，剔除其中明显的误匹配，通过设定阈值即可获得相对精确的匹配对。图像多尺度配准的小波域SURF算法步骤如下所示。

图像多尺度配准的小波域SURF算法：

步骤1对参考图像和待配准图像进行N层小波分解。

步骤2对参考图像和待配准图像的第i=N层低频子图像分别提取SURF特征，并进行特征匹配，得到该尺度下的匹配对，估计初始变换参数。

步骤3对第i=N-1层低频子图像提取SURF特征，然后进行特征匹配，并利用上层得到的初始变换参数剔除误匹配，并更新变换参数。

步骤4重复步骤3，直至参考图像和待配准图像，剔除误匹配，并估计变换参数。

步骤5得到最终的变换参数后，利用双线性插值法将待配准图像重采样至参考图像的坐标系下即可得到配准结果。

在上述步骤中，需要注意在步骤2中对第i=N层低频子图像提取SURF并匹配时，鉴于其中也有可能存在误匹配，而且它是最底层的，无法利用上层的变换参数，此时可以利用最小二乘法剔除与变换参数距离最大的匹配对，直到所有的匹配对与变换参数的差异小于某个特定的像素阈值为止。在步骤3中剔除误匹配是通过剔除与上层的变换参数距离大于某个阈值的匹配对来完成的。经过上述步骤，就能得到比原始SURF方法更高的正确匹配率，降低误匹配对对变换参数的影响。

4 实验结果及分析

本文中所有实验均由MATLAB7.0实现，运行计算机的处理器为Intel CoreTMi5-2400 CPU@3.1 GHz，内存2.99 GB。为了验证本文方法在剔除误匹配方面的有效性，下面分别针对光学遥感图像和SAR图像进行配准实验。实验首先采用SURF匹配算法对参考图像和待配准图像进行特征匹配，可以得到原始图像最初的匹配对，然后利用本文提出的多尺度配准的小波域SURF算法，利用上层得到的变换参数，逐层剔除误匹配，直至最后参考图像和待配准图像的配准。

图1 SURF算法初始匹配对，距离比为0.75

（1）光学遥感图像的配准

图1（a）（b）所示为两幅Landsat TM图像，大小均为600×600；对于SURF算法，当距离比为0.55时在两幅图中仅可以找出6个匹配对，随着参数的增大会出现更多的匹配，但其中明显的误匹配数目也随之增加，如图1（c）所示，无法进行有效的参数估计；应用本文方法对参考图像和待配准图像进行N=2层小波分解，提取SURF特征，并利用最小二乘法剔除错误匹配，可以得到8个精确的初始匹配对，如图2（a）所示，计算初始的变换参数，并利用这个初始的变换参数剔除第一层小波分解上的误匹配，得到50个精确的匹配对，如图2（b）所示，计算变换参数，利用这个变换参数剔除第零层小波分解图像上的误匹配，可得到最终的46个精确的匹配对，如图2（c）所示，利用这46个匹配对估计参考图像和待配准图像间的变换参数，对图像进行重采样并得到最终的配准结果，如图2（d）所示。图3所示为另外两幅Landsat TM图像的配准结果，初始匹配对为164对，存在错误匹配，利用本文方法逐层剔除误匹配，得到最终的28个精确匹配对，如图3（c）所示。对于光学遥感图像，在剔除误匹配时本文中设定像素阈值为4，因为像素阈值太小的话最终得到的正确匹配点对个数非常少，会影响配准精度。

图2 本文算法得到的配准结果（光学遥感影像1）

图3 本文算法得到的配准结果（光学遥感影像2）

图4 本文算法得到的配准结果（唐家山堰塞湖SAR影像）

图5 本文算法得到的配准结果（白水河水库SAR影像）

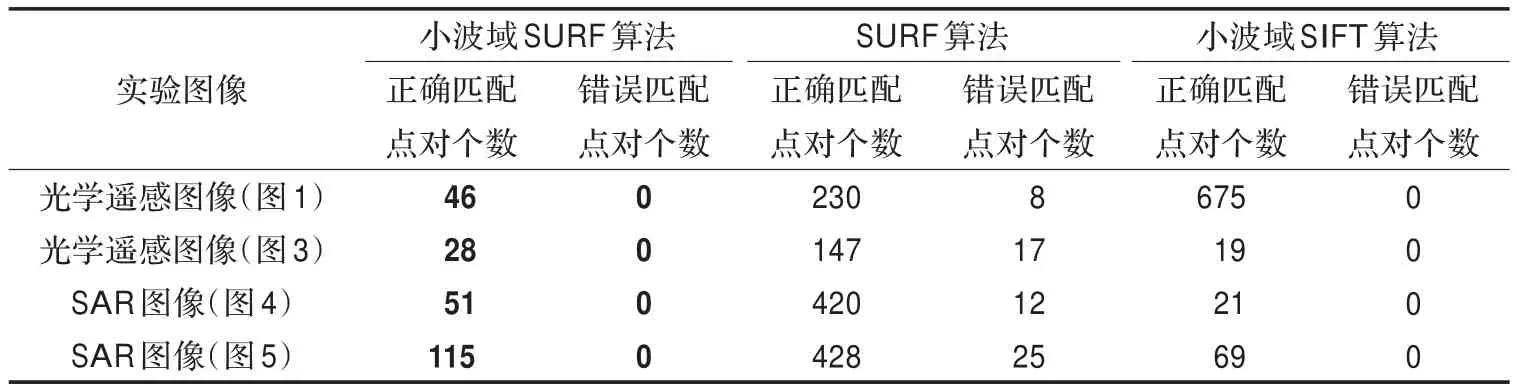
表1 结果比较1（正确匹配对与错误匹配对个数）

表2 结果比较2（配准误差与运行时间1））

（2）SAR图像的配准

2008年5月我国四川汶川地区发生了大地震，本文使用汶川地震前后唐家山堰塞湖及其周边地区的图像，对两幅图像进行配准得到432个初始匹配对，存在错误匹配，利用本文方法逐层剔除误匹配，得到最终的51个精确匹配对。图4为本文方法所得到的结果。图5为对绵阳市白水河水库震前和震后的图像利用本文方法得到的配准结果。对于SAR图像，其本身提取的SURF特征点数较多，因此在剔除误匹配时可将像素阈值设定相对较小，本文中设为1.5。

对于上面的光学遥感图像和SAR图像，将本文方法与原始的SURF方法及小波域SIFT方法[14-15]进行了比较，对比结果如表1和表2所示。

由表1和表2的结果可以看出，无论是对于光学遥感图像还是SAR图像，小波域SURF算法都能较好地剔除原始SURF算法中的错误匹配，提高了配准精度；运行时间比原始SURF算法长是因为本文算法对图像进行了小波分解，对于各层不同分辨率的分解图像都要进行SURF特征提取，并不是只对原始图像进行特征提取。

本文算法与小波域SIFT算法相比，配准精度要优于小波域SIFT算法，并且对于两幅SAR图像而言，RMSE均小于一个像素，说明本文方法在应用于SAR图像配准时也较为有效。在运行时间上，对于特征点数较少的光学遥感图像而言二者的运行时间相差不大，但是对于SAR图像而言，由于其提取的特征点数较多，本文算法的效率明显高于小波域SIFT算法。

5 结论

由于SURF描述子仅利用了特征点的局部邻域信息，对于局部场景发生变化的图像容易产生误匹配，进而影响变换参数的估计及最终的配准精度。针对这个问题，本文研究了图像多尺度配准的小波域SURF算法，先对图像进行小波分解，然后利用低分辨率图像上得到的变换参数剔除高分辨率图像上的错误匹配，得到相对精确的匹配点对，提高了正确匹配率。通过在真实图像上的实验结果分析，验证了本文方法的有效性和可行性。

[1]Brown L G.A survey of image registration techniques[J]. ACM Computing Surveys，1992，24（4）：326-376.

[2]延伟东.SAR图像配准的几类结构模式匹配方法研究[D].西安：西北工业大学，2012.

[3]刘向增.SAR图像配准的几类稳健局部特征描述子研究[D].西安：西北工业大学，2011.

[4]Wang S，Xiao J，Jiao L，et al.Fast and accurate automatic SAR image registration using seven invariant moments and improved chain coding of region boundaries[C]//Proceedings of SPIE MIPPR 2007：Multispectral Image Processing，2007.

[5]Castro E D，Morandi C.Registration of translated and rotated images using finite fourier transforms[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1987，9（5）：700-703.

[6]Wang Z，Wu F，Hu Z.MSLD：a robust descriptor for line matching[J].Pattern Recognition，2009，42（5）：941-953.

[7]Lowe D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision，2004，60（2）：91-110.

[8]Ke Y，Sukthankar R.PCA-SIFT：a more distinctive representation for local image descriptors[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition，2004：506-513.

[9]Mikolajczyk K，Schmid C.A performance evaluation of local descriptors[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27（10）：1615-1630.

[10]Duan C，Meng X，Tu C.How to make local image featuresmoreefficient anddistinctive[J].IET Computer Vision，2008，2（3）：178-189.

[11]Bay H，Ess A，Tuytelaars T，et al.Speeded-Up Robust Features（SURF）[J].Computer Vision and Image Understanding，2008，110（3）：346-359.

[12]Juan L，Gwun O.A comparison of SIFT，PCA-SIFT and SURF[J].International Journal of Image Processing，2009，3（4）：143-152.

[13]Hong Gang，Zhang Yun.Wavelet-based image registration technique for high-resolution remote sensing images[J]. Computers&Geosciences，2008，34：1708-1720.

[14]武建明，田铮，刘向增.图像多尺度配准的小波域SIFT方法[J].西北工业大学学报，2011，29（1）：17-21.

[15]武建明.SAR图像多尺度配准的两类变换域SIFT方法[D].西安：西北工业大学，2011.

WEI Jianlong1,TIAN Zheng1，2,YAN Weidong1,FAN Ming1

1.School of Science,Northwestern Polytechnical University,Xi’an 710129,China
2.State Key Laboratory of Remote Sensing Science,Institute of Remote Sensing Applications,Chinese Academy of Sciences, Beijing 100101,China

A method to correct Speed-Up Robust Features（SURF）mismatching combining wavelet transform with SURF is proposed to solve the mismatching in the registration of the images broken in the locate structure.This paper applies wavelet decomposition to the images.It utilizes the transformation parameters derived from images of lower resolution,and a number of mismatching points of higher resolution are eliminated.Then images are registrated using the exact matching points.The experimental results on optical-remote sensing images and SAR images show that the proposed algorithm can eliminate the mismatching points effectively and enhance the registration accuracy.

image registration;Speed-Up Robust Features（SURF）;wavelet domain;multiscale

A

TP391

10.3778/j.issn.1002-8331.1211-0273

WEI Jianlong,TIAN Zheng,YAN Weidong,et al.Image multiscale registration in wavelet domain using SURF. Computer Engineering and Applications,2014,50（21）：200-204.

国家自然科学基金（No.60972150，No.61201323）；西北工业大学基础研究基金（No.JC20110277）。

卫建龙（1987—），男，在读硕士，主要研究方向：图像处理与模式识别；田铮（1946—），女，教授，主要研究方向：遥感图像处理与模式识别，谱图理论，非线性时间序列的理论与方法，多尺度随机模型等；延伟东（1979—），男，博士，讲师，主要研究方向：遥感图像处理。E-mail：841217489@qq.com

2012-11-23

2013-01-10

1002-8331（2014）21-0200-05

CNKI出版日期：2013-03-13，http://www.cnki.net/kcms/detail/11.2127.TP.20130313.0946.008.html