基于统计假设测试的噪声方差估计方法
王静,王晅,蒋平
1.陕西师范大学物理学与信息技术学院,西安 710062
2.榆林学院,陕西榆林 719000
基于统计假设测试的噪声方差估计方法
王静1,王晅1,蒋平2
1.陕西师范大学物理学与信息技术学院,西安 710062
2.榆林学院,陕西榆林 719000
在数字图像处理中,噪声方差估计是一个重要的研究课题。提出一种针对加性高斯噪声的噪声方差估计方法。利用一种基于统计假设测试的方法来度量图像结构特征度,基于图像结构特征度找出平滑子块和非平滑子块(含有边缘或纹理子块);以平滑子块中的最小方差为参考方差,选择出方差与参考方差相差在一定范围内且不含边缘的所有子块;从选出的子块中求以图像结构特征度为权重的方差平均值作为噪声方差估计值。相比于现有的噪声估计方法,该方法具有非常高的估计精度,适合感染高斯噪声的各种图像。
白高斯噪声;噪声图像;噪声估计;统计假设测试
1 引言
在数字图像处理过程中,很多图像处理算法把噪声方差作为已知参数,例如:去噪算法[1-3]、运动检测算法[4]、图像分割算法[5]等,但是在实际中噪声图像的噪声方差是未知的,所以如何精确地估计噪声方差是一个重要的研究课题。
现有的噪声方差估计算法主要分为两类:基于滤波方法[6-8]和基于分块方法[9-11]。基于滤波方法的主要思路是从噪声图像中分离出高频信息,再从分离出的高频信息中估算出图像的噪声方差。由于分离出的高频信息中含有图像的边缘或纹理信息,对边缘纹理信息较为丰富的图像,此类方法会产生较大的估计误差。针对滤波方法存在的这一问题,随后出现了基于分块的方法,该类方法是把噪声图像分成很多小块,从这些小块中寻找平滑子块,然后基于这些平滑子块估计图像的噪声方差。这类算法的性能主要取决于如何在含噪图像中精确定位平滑子块。此外,还有一些其他的方差估计算法[12-14]。
2005年,Shin等提出了一种使用自适应高斯滤波器的基于分块的噪声估计方法[9],该方法与传统分块方法有所不同,它是一种分块与滤波结合的混合方法,先通过局部方差最小的方法来寻找平滑子块,找出所有平滑子块后,对这些平滑子块使用自适应高斯滤波算法,便可估计出噪声方差。但是局部方差最小并不是度量平滑度的最好方法,因此该方法对于低噪声图像的估计效果较好,而对于高噪声图像的估计效果很差。2005年,Amer提出了一种面向结构的估计高斯白噪声方差的方法[10],该算法使用一种结构分析器来计算平滑度,然后以平滑度最小的三个子块的方差中值为参考方差,找出所有方差与参考方差相差小于阈值的子块,然后对这些块的方差求平均。该方法有两个缺点:一是存在非常严重的过估计,二是估计结果很不稳定。2012年,J.Tian等提出了一种使用变化的自适应进化算法来估计噪声方差的方法[11],该方法通过蚁群技术来寻找平滑区域,在低噪声时对复杂图像的估计结果不理想,高噪声时效果非常好,但是这个技术需要大量的计算,时间复杂度较高。
2005年,Kim等提出了一种利用统计假设测试原理来度量图像结构特征的方法[15],通过图像结构特征度可以判断出图像局部区域是结构区域还是平滑区域。该方法主要应用于各种视频增强算法中,例如当存在时变的噪声信号时对视频进行降噪和清晰度增强。基于此,本文提出了一种基于统计假设测试的噪声方差估计方法,该方法根据图像结构特征度找出平滑子块和非平滑子块(含有边缘或纹理子块);然后以平滑子块中的最小方差为参考方差,选择出方差与参考方差相差在一定范围内且属于平滑子块的所有子块;最后从选出的子块中求以图像结构特征度为权重的方差平均值作为噪声方差估计值。实验结果表明,本文的方法估计精度高稳定性好,计算复杂度低,适合感染高斯噪声的丰富纹理图像。
2 本文方法
2.1 基本原理
大多数的图像噪声方差估计算法中,噪声信号通常假设为独立同分布的加性的具有固定零均值的高斯噪声,对于方差未知的零均值加性高斯噪声图像一般有如下模型:

其中I(x,y)是噪声图像,S(x,y)是原始图像,η(x,y)是加性高斯噪声。噪声估计的目的就是从噪声图像中估计噪声方差。
以像素I(i,j)为中心,大小为W×W的平滑子块表示为:
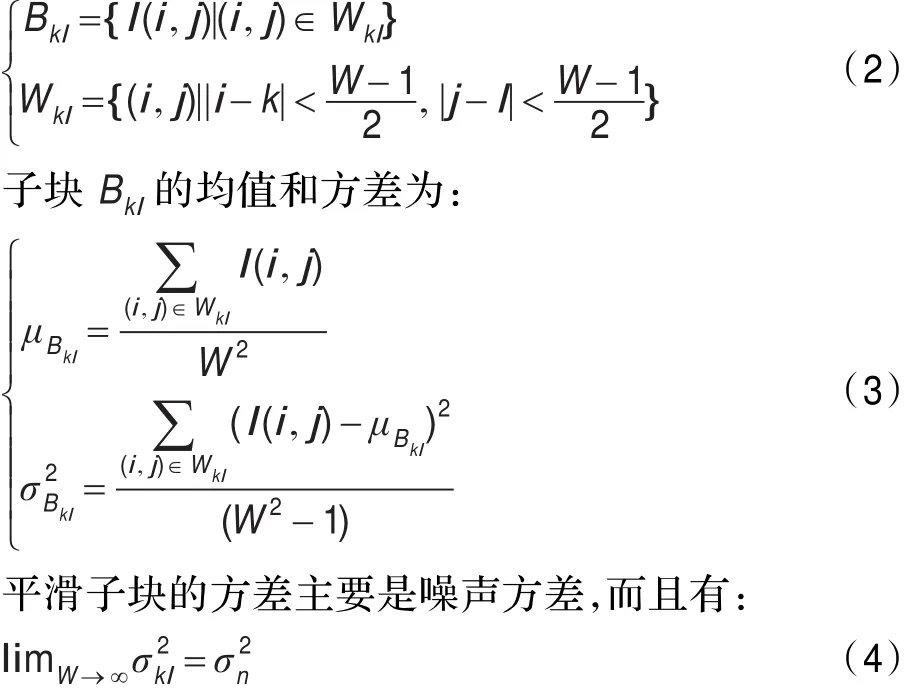
所以只要有足够的平滑子块就能精确地估计出σ2n。本文提出的方法主要有两个步骤:平滑块的选择以及对这些平滑块进行噪声方差估计。
2.2 图像结构特征度
Kim等提出了一种利用统计假设测试原理来度量图像结构特征的方法[15],通过图像结构特征度可以判断出图像局部区域是结构区域还是平滑区域。该方法的基本思想就是在一个结构区域至少在某一个方向上具有很强的采样关系,而在纯噪声区域则没有一个方向上具有很强采样关系。简单地说,如果一个区域是结构区域,则该区域至少有一条明显的边缘或纹理,而在平滑区域则没有明显的边缘或纹理方向。在四个方向上重新排列像素值的示例如图1所示。
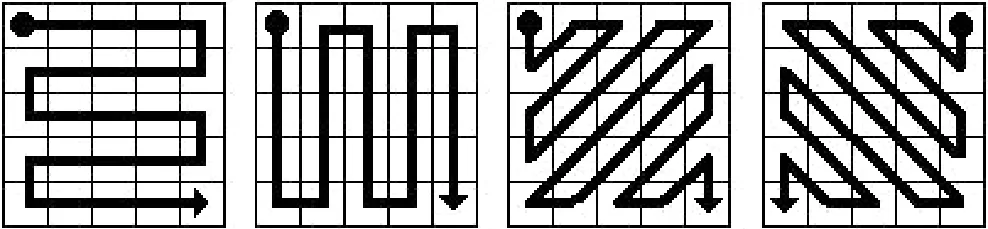
图1 在四个方向上重新排列像素值的示例
定义图像结构特征矢量如下:

其中θ={θ1,θ2,…,θm},是把区域Bkl的像素值按照方向θ重新排列后的结果。图1是对5×5的区域按照4个方向进行像素值重列的示例,其方向θ={0°,90°,45°,135°},如图中的箭头所示。
为了更直观地理解采样关系,重新定义图像结构特征如下:


2.3 自适应选择平滑子块方法
虽然通过图像结构特征度δkl可以找出非常平滑子块,但是在丰富纹理图像中非常平滑子块的数量很少,不足以估计出噪声方差,所以需要另外一种寻找平滑子块的方法。

第一个条件确保被选择子块的方差于参考方差相差在一定范围内,第二个条件保证含边缘或纹理的子块不被选中。δkl为0的非常平滑子块中必定含有真正的平滑子块,参考方差不会远超过实际噪声方差,所以不会产生过估计。并且δkl为0的子块数量很多,尤其是在较少纹理图像中有成百上千块,从大量子块中选择出的参考方差要比只从三个子块中选择的参考方差稳定得多,所以估计结果比较稳定。
2.4 加权估计噪声方差
找到大量平滑子块后,就从这些子块中计算出噪声方差,一般方法是求这些子块方差的平均值。本文方法选择出的所有平滑子块中,并不是所有子块的δkl都趋近于0,有的子块含有一些小结构,应该减小这些子块对结果的影响,例如:δkl越大,对结果的影响越小。所以本文以δkl为加权来计算估计方差σ2e,方法如下:

其中V是平滑子块的集合。
3 实验仿真及分析
为了说明本文算法的有效性,分别在9幅512×512的图像(图2)上测试本文算法,添加的测试噪声的标准差σn分别为0,5,10,20,30,40。本文对每幅图像每个方差都进行10次实验,实验中对图像进行分块为大小5×5且不重叠的块,参数C0和C1取值分别为1.105和2.604(详见文献[15])。

图2 512×512测试图像
第一个实验是本文方法与参考文献[6-11]其他的一些经典方法进行的对比,通过计算估计结果的平均误差和误差方差来度量算法的性能。平均误差和误差方差的计算方法如下:
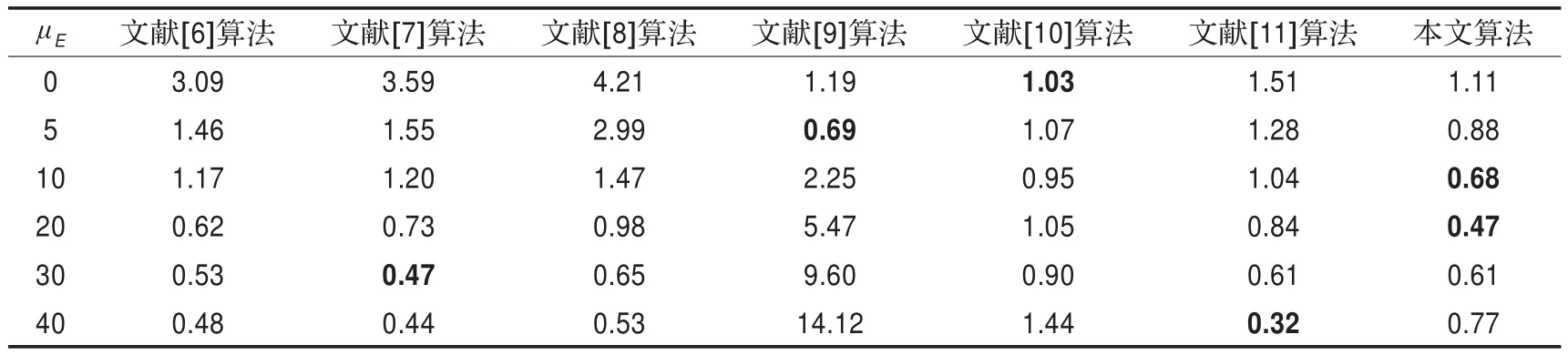
表1 本文方法与其他方法的平均误差比较
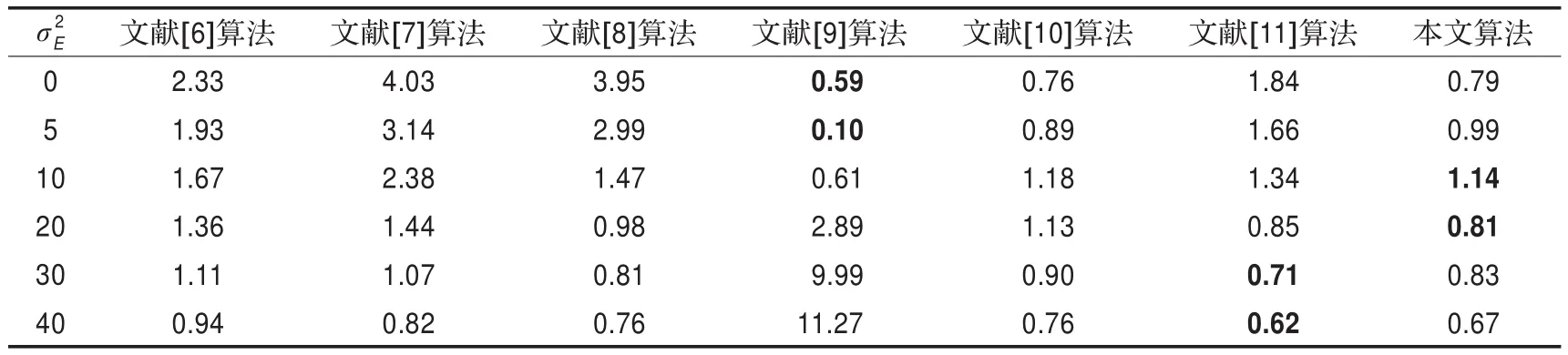
表2 本文方法与其他方法的误差方差比较
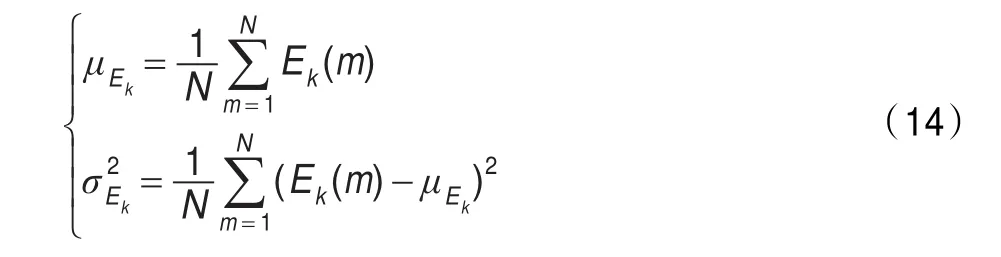
其中Ek=|σn-σe|是估计误差,N是图像数量。
表1和表2给出了平均误差和误差方差的对比结果。从表1和表2中可以看出本文算法具有一定的优势,大多时候比其他算法具有更好的性能,并且估计结果比较稳定。与文献[9-11]这三种基于分块方法进行比较,可以看出,在低噪声水平时,本文算法和文献[9-10]算法比其他算法明显有优势,这是因为这几种算法适合低噪声复杂图像,而其他算法受到边缘纹理影响有比较大的误差。在高噪声水平时,文献[9]的估计效果非常差,因为该算法是以局部方差最小的子块为平滑块,噪声方差越大,子块最小的方差于真实方差相差就越大,因此导致高噪声时估计误差很大。文献[11]和本文算法在高噪声时性能较好,适合于感染高噪声的复杂图像的方差估计。
第二个实验是本文方法与Amer方法在过估计和稳定性方面进行的对比。表3是从实验中所挑选出的一些Amer方法存在严重过估计的情况。从表3中的参考方差和估计方差的结果明显能看出,Amer方法可能发生严重过估计,而本文方法不存在这个问题。表4给出了两种方法的参考标准差σr和估计方差σe。该数据是对Lena图像随机添加噪声的标准方差为σn=30然后进行了10次实验得出的,从表4中看出,Amer方法的参考方差不稳定,导致最终的估计结果不稳定,本文方法的估计结果比Amer方法稳定。这里只列举了对σn=30的Lena图像的10次实验结果对比,实际上在所有实验中本文方法都比Amer方法稳定。
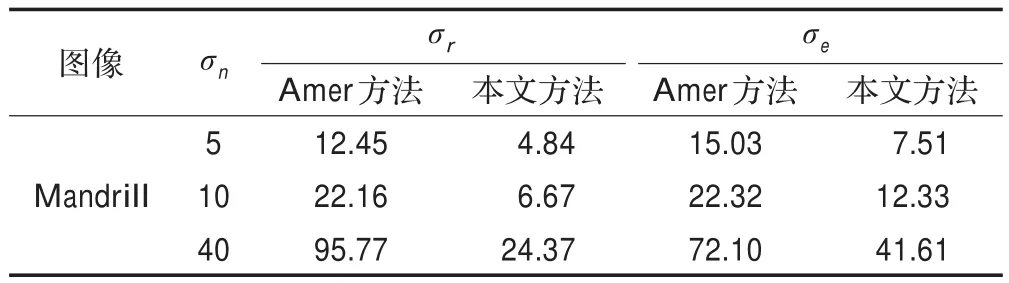
表3 Amer方法在实验中的一些严重过估计
最后,对算法的执行时间进行对比。模拟实验用的计算机配置为奔腾双核1.60 GHz、1 GB内存,操作系统为XP,程序语言是MATLAB7.0。本文算法和文献[6-11]中算法的执行时间如表5所示,从表5中可以看出,基于滤波方法文献[6-8]的算法计算时间要短一些,因为滤波方法计算复杂度低。基于分块方法中本文方法和文献[9-10]算法的计算复杂度相对来说是比较小的,执行时间比较快,而文献[11]的方法计算需要大量的计算时间,计算复杂度高。

表4 本文方法与Amer方法的稳定性比较(σn=30的Lena图像)

表5 本文方法与其他方法的计算复杂度比较
4 结束语
本文提出了一种基于统计假设测试的噪声方差估计方法,该方法估计精度高、稳定性好,计算复杂度低,适合感染高斯噪声的丰富纹理图像,与一些传统方法相比较,本文方法在高噪声和低噪声都具有较好的性能,并且本文方法有两个优点:一是在估计含有边缘和丰富纹理图像的噪声方差时,估计精度高,不会产生过估计;二是估计结果稳定性好。
[1]Lee J S.Digital image enhancement and noise filtering by use of local statistics[J].IEEE Trans on Pattern Anal Mach Intell,1980,2(2):165-168.
[2]Gilboa G,Sochen N,Zeevi Y Y.Estimation of optimal PDE-based denoising in the SNR sense[J].IEEE Trans on Image Processing,2006,15(8):2269-2280.
[3]Wong A,Mishra A,Zhang W,et al.Stochastic image denoising based on Markov-chain Monte-Carlo sampling[J].Signal Processing,2011,91(8):2112-2120.
[4]Calvagno G,Fantozzi F.Model-based global and local motion estimation for video conference sequences[J].IEEE Trans on Circuits and Systems for Video Technology,2004,14(9):1156-1161.
[5]Spann M,Wilson R.A quad-tree approach to image segmentation which combines statistical and spatial information[J]. Pattern Recognition,1985,18(3/4):257-269.
[6]Olsen S I.Estimation of noise in images:an evaluation[J]. CVGIP:Graphical Models and Image Processing,1993,55(4):319-323.
[7]Donoho D L,Johnstone I M.Ideal spatial adaptation by wavelet shrinkage[J].Biometrika,1994,81(3):425-455.
[8]Immerkær J.Fast noise variance estimation[J].Computer Vision and Image Understanding,1996,64(2):300-302.
[9]Shin D H,Park R H,Yang S,et al.Block-based noise estimation using adaptive gaussian filtering[J].IEEE Trans on Cousumer Electronics,2005,51(1):218-226.
[10]Amer A,Dubois E.Fast and reliable structure-oriented video noise estimation[J].IEEE Trans on Circuits and Systems for Video Technology,2005,15(1):113-118.
[11]Tian J,Chen L.Image noise estimation using a variationadaptive evolutionary approach[J].IEEE Signal Processing Letters,2012,19(7):395-398.
[12]Hashemi M,Beheshti S.Adaptive noise variance estimation in Bayes shrink[J].IEEE Signal Processing Letters,2010,17(1):12-15.
[13]Yang S M,Tai S C.Fast and reliable image noise estimation using a hybrid approach[J].Journal of Electrical Imaging,2010,19(3).
[14]Pei Z J,Tong Q Q,Wang L,et al.A median filter method for image noise variance estimation[C]//Second International Conference on Information Technology and Computer Science,Kiev,Ukraine,2010.
[15]Kim Y H,Lee J.Image feature and noise detection based on statistical independent tests and their applications in image processing[J].IEEE Trans on Consumer Electronics,2005,51(4):1367-1378.
WANG Jing1,WANG Xuan1,JIANG Ping2
1.College of Physics and Information Technology,Shaanxi Normal University,Xi’an 710062,China
2.Yulin University,Yulin,Shaanxi 719000,China
Image noise estimation is a very important research topic in digital image processing.This paper presents a fast and reliable noise estimation algorithm for additive white Gaussian noise.The proposed algorithm provides a way to measure the degree of image feature based on Statistical Hypothesis Tests(SHT).The proposed algorithm distinguishes homogeneous blocks and non-homogeneous blocks by the degree of image feature.It sets the minimal variance of these homogeneous blocks as a reference variance.And then it finds more homogeneous blocks whose variances are similar to the reference variance and which not contain edge.The noise variance is estimated from these homogeneous blocks by a weighted averaging process according to the degree of image feature.Compared with the existing noise estimation methods,the proposed algorithm performs well in the estimation precision and suitable for the Gaussian noise-infected images.
white Gaussian noise;noisy image;noise estimation;statistical hypothesis tests
A
TP391
10.3778/j.issn.1002-8331.1211-0281
WANG Jing,WANG Xuan,JIANG Ping.Noise variance estimation method based on statistical hypothesis tests. Computer Engineering and Applications,2014,50(21):166-170.
王静(1983—),女,硕士研究生,主研方向:图像处理,噪声估计;王晅(1966—),男,博士,教授,主研方向:图像处理、模式识别;蒋平(1979—),男,讲师,主研方向:计算机视觉。E-mail:2008-ytt@163.com
2012-11-23
2013-01-21
1002-8331(2014)21-0166-05
CNKI出版日期:2013-02-28,http://www.cnki.net/kcms/detail/11.2127.TP.20130228.1148.019.html

