基于FPGA的KLT特征点多层次归并排序
柴志雷,方万元
江南大学物联网技术应用教育部工程研究中心,江苏无锡 214122
◎图形图像处理◎
基于FPGA的KLT特征点多层次归并排序
柴志雷,方万元
江南大学物联网技术应用教育部工程研究中心,江苏无锡 214122
KLT算法已在多个领域得到成功的应用,其中特征点的排序是用来选择好的特征点跟踪的关键。针对传统排序算法计算耗时、实时性差的缺点,提出一种可并行的多层次归并排序算法并在FPGA中实现了其并行计算,同时分析了其周期精确的计算时间。结果表明该归并排序算法可以O(N)的时间复杂度完成特征点的排序,能够满足高清分辨率的图像/视频数据中KLT特征点排序的实时性要求。
归并排序;KLT;现场可编程门阵列(FPGA)排序
Kanade-Lucas-Tomasi(KLT)[1-4]算法是一种基于特征点的跟踪算法。它的计算实时性和算法稳定性使其在图像处理的各个领域受到广泛关注。KLT算法分为特征点提取和特征点跟踪。特征点提取之后,选取合适的特征点是提高跟踪鲁棒性的关键。一般选取的方法利用特征点的特征值进行排序,特征值较大的点为较好的跟踪特征点。
随着高清时代的到来,传统的通用PC下的KLT算法对于高清资源,例如720P(1 280×720),1 080P(1 920× 1 080)的图片处理无法再达到实时的要求。硬件平台下的实时KLT算法就显得尤为重要。FPGA提供了一个灵活的快速原型设计和并行计算的平台。
排序算法在科学计算领域已经有极其详尽的研究,已有许多成熟的排序算法[5]。近年来,在不同的应用下也提出了多种基于FPGA的排序方法。根据应用的不同,基于FPGA的排序一般分为两类:基于网络的排序[6-7]和基于线性数组的排序[8]。
基于网络的排序一般使用两输入的交换比较器来排序。Zhang Y.采用了固定大小的排序网络[7],分为输入队列、乒乓排序网络和输出检测模块。Martinez等[6]提出了应用在块排序压缩上的网络排序算法,采用了乒乓操作,实现数据循环处理。排序单元处理128个字符,最终的结果显示可达到的最大时钟频率为50 MHz左右。基于线性数组的排序基于可扩展的线性数组。Paraham,Kwai[8]采用比较/插入单元。每个单元包含比较器,乘法器和控制单元。可扩展线性数组包含一系列的单元。
K.Ratnayake和A.Amer提出了计数排序算法[9]。不过是在BRAMS上实现排序算法,较为复杂。M.Edahiro[10]在EDK的开发环境下实现了并行的排序算法。吴彦宏的堆排序算法[11]是在SRAM上实现基于队列的数据堆排序,实现较为复杂。
纵观以上排序算法,有的是针对特殊应用的排序,有的在对有限的数据排序的时候,资源利用率较高的同时,最大时钟频率很低。无法满足对于高清实时图片的特征点排序的要求。
本文首先分析了通用PC下的基于归并操作的归并排序,然后提出了一种基于FPGA的并行的多层次归并排序结构,并将其应用于KLT特征点的排序。多层次归并排序结构由分为基于寄存器的归并组件实现和基于FIFO的归并组件构成。可以根据FPGA开发板的寄存器和FIFO资源灵活配置组件。分析了多层次归并排序结构的时间周期。在ISIM仿真之后又在XC5VSX50T-1ff1136开发板上得以实现,在此基础上分析了其在开发板上的资源利用率和最大时钟周期。结果表明本文的归并排序完全可以满足高清图片下KLT特征点的实时排序要求。
1 经典归并排序
1.1 归并操作
归并操作是将两个(或两个以上)有序队列合并成一组新的有序表。若已知两组有序队列分别为1,3,5和2,4,6。如图1所示为两路归并操作。A,B分别为已排完序的有序队列。C为A,B的归并结果。图1为一次完整归并操作的示意图。
归并步骤:
(1)分别取A,B的队头,设为a,b。比较a,b两者的大小(比较操作)。
(2)将a,b中较大者出队,放入缓存tmp中(出队操作)。
(3)将tmp压入C的队尾(入队操作)。
重复(1)~(3)直到A,B中一个为空。执行(4)。
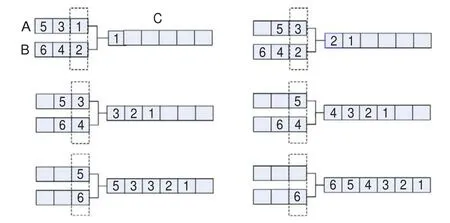
图1 归并操作示意图
(4)若A/(B)为空,将B/(A)队头放入tmp中(出队操作)。
(5)将tmp压入C的队尾(入队操作)。
重复(5)~(6)直到A,B两者都为空。
1.2 基于归并操作的排序
设待排序的数列为D[n],数列长度为N。
归并排序步骤:
将D[n]分为N个已排完序的长度为1的队列。两两之间运行用1.1节中的归并操作,合并成floor[n/2]个两两有序的队列。
循环进行上述步骤,两两之间进行归并操作,直到最后合并成一个N有序的队列。
归并排序的如图2。

图2 基于归并操作的归并排序
基于PC的归并操作时间复杂度是O(N lg(N))。空间复杂度是O(N)。
2 可并行归并排序
观察经典的PC下的归并排序。队列可以用寄存器或者FIFO实现。分别用寄存器和FIFO来实现归并操作。当待排序的队列长度较小时使用基于寄存器的归并。当长度较大时使用基于FIFO的队列。
归并排序可以分解为若干层归并操作,每一层的归并操作的输入是上一层的输出。每层的归并操作的差别是队列的长度。归并操作的硬件结构为:(1)存储的队列;(2)比较器;(3)辅助的控制器。归并操作的行为:(1)队列的基础行为(出队,入队,判断空满);(2)归并输入;(3)归并输出。假设待排序的队列长度为N。
2.1 基于寄存器的归并操作
硬件结构:
队列:队列长度为N:N个寄存器R1,R2,…,RN,其中R1为队头,RN为队尾。
比较器:排序的数据位n位,采用n位的比较器。由上升沿触发。
辅助控制器:每个队列有一个标记位FLAG,用一个标记位FLAG来计数。初始为0,入队时标记加1,出队时标记减1。一组队列(两个)有一个标记位BUFFFLAG。用来判断组之间的输入输出切换,实现多组的乒乓操作。
行为描述(以下操作均为一个时间周期内,由上升沿触发):
2.1.1 队列行为
(1)出队操作,OUT<=R1;R1<=R2;R2<=R3;…;R(N-1)<=RN。
(2)入队操作,R1<=R2;R2<=R3;…;R(N-1)<= RN;RN<=IN。
(3)判断队列是否为空,FLAG为0时,队列空;FLAG等于N,队列满。
2.1.2 归并输入
(1)在T∈[1,N]时,A依次入队,队列标记位加1。组标记位加1。
(2)在T∈[N+1,2N]时,B依次入队,队列标记位加1。组标记位加1。
2.1.3 归并输出
(1)在A,B非空时(即A_FLAG>0,B_FLAG>0),比较A,B的队头。输出其中较大者;并将其队头出队;将其队列标记减1。组标记位减1。OUTENABLE为1。
(2)当A,B任一为空时,依次输出另一队列,将其标记减1,组标记位减1。OUTENABLE为0;直到A,B均为空,OUTENABLE为0。
以上步骤可见基于寄存器的归并操作步骤和经典的PC操作几乎一样。因为在基于寄存器实现的时候,出队,入队,取队头,比较大小都可以在同一个时钟周期内实现,所以可以直接用时序逻辑实现。
硬件结构图如图3所示。
2.2 基于FIFO的归并操作
当基于FIFO实现的时候,入队,出队要依靠W,R信号位来控制。当一个上升沿后设置R=1,等一个时钟周期才能获得FIFO队头数据。若比较器用时序逻辑实现,则需要再等一个时钟周期之后,才能比较两个队头数据。那么数据的输出比输入多一倍的时钟周期,无法组合成乒乓操作和并行的多层次结构。所以将FIFO的控制用时序逻辑实现,而将比较器用组合逻辑实现。从而实现输入,输出的时钟周期数相等。
硬件结构:
队列:FIFO队列。FIFO长度为2M(大于等于N)。
FIFO的硬件结构见图4。有数据输入输出端口,和读信号W,写信号R,以及空满信号。

图3 乒乓操作的寄存器归并操作

图4 基于FIFO的归并操作
比较器:排序的数据位n位,采用n位的比较器。采用组合逻辑实现。
时序逻辑辅助控制器:每个队列有一个读信号:W,写信号R1,有一个标记位FLAG,用一个标记位FLAG来计数。初始为0,入队时标记加1,出队时标记减1。一组队列(两个)有一个标记位BUFFFLAG。用来判断组件的输入输出切换,实现多组的乒乓操作。
组合逻辑辅助控制器:每个队列有一个额外的读信号R1,由比较器的比较结果控制R2。
2.2.1 队列行为
(1)出队操作,FIFOIN<=IN;R<=1。
(2)入队操作,OUT<=FIFOOUT;W<=1。
(3)判断队列是否为空,FIFO自己空满信号。不过一般FIFO的长度和有序队列的长度不等,所以还是用FLGA来判断。FLAG为0时,队列空;FLAG等于N,队列满。
2.2.2 归并输入
将A的队头和B的队尾衔接。数据始终由A的队尾插入,再由A的队头插入B的队尾。AB由A_FIFOOUT和B_FIFOIN衔接。等价模型就是AB中间加了2个寄存器;具体见图4。
(1)A的队头和B的队尾衔接;B_FIFIIN<=A_ FIFOOUT。
(2)数据输入A,T∈[1,2N]时,A_W<=1。
(3)数据输入B,T∈[N+1,2N]时B_W<=1。
(4)AB中有2个寄存器,所以A的R信号要比B的W信号提取2个周期,即T∈[N-1,2N-2]时A_R1<=1。
2.2.3 归并输出
输出的控制分为时序逻辑和组合逻辑,FIFO的控制用时序逻辑,由上升沿触发。比较器及依据判断结果设置R2,用组合逻辑。
时序逻辑:
当T=2N-1,同时取AB队头,即A_R1<=1;B_R1<=1。
组合逻辑:
当T∈[2N,4N]时,T时刻设置A,B的R2信号,T+1,A,B的队头更新,比较两者大小,根据比较结果设置AB的R2信号。
(1)A_R<=A_R1|A_R2;B_R<=B_R1|B_R2。
(2)在A,B非空时(即A_FLAG>0,B_FLAG>0),比较A,B的队头。输出其中较大者,并将其队头出队,设置其R2等于1,将其标记减1。组标记位减1。OUTENABLE为1。
(3)当A,B任一为空时,依次输出另一队列,将另一队列标记减1,组标记位减1,设置另一队列R2等于1,OUTENABLE为0。直到A,B均为空,OUTENABLE为0。
2.3 乒乓的归并操作
如图3,图4中设置两队列,实现乒乓操作。用BUFFFLAG切换每一组的输入输出。
(1)T∈[1,2N]时,组AB输入;OUTENABLE<=0。
(2)T∈[2N+1,4N]时,组AB输出,组CD输入;OUTENABLE<=1。
(3)T∈[4N+1,6N]时,组CD输出,组AB输入;OUTENABLE<=1。
循环执行(2),(3)直到所有的数据都变成2N有序的输出。
2.4 基于归并操作的排序
不论是基于寄存器的归并操作,还是基于FIFO的归并操作,都可以看成一个归并组件,作为归并排序的一层。它们拥有统一的接口。
归并组件接口:
输入:
INDATA:待排序数输入端口
INENABLE:输入使能信号。INENABLE为1时INDATA有效
输出:
OUTDATA:待排序数输出端口
OUTENABLE:输出使能信号。OUTENABLE为1时OUTDATA输出有效
如同1.2节所述,将归并排序分多层,首先是长度为1,最后一层是长度为N/2。上一层的输出和下一层的输入衔接,并通过上一层的OUTENBALE信号,控制下一层的归并的开始。第一层输入原始的待排序数据,最后一层无需乒乓操作,只使用一组队列就可以输出排序之后的数据。
可以灵活地选用基于寄存器的组件和选用基于FIFO的组件搭配,实现小规模数据和大规模数据下不同的配置。
在KLT跟踪算法里实际使用的是图片特征点的坐标位置,所以在排序的存储队列中,将一个点的特征值和坐标位置同时存储。归并排序时的比较器只使用特征值比较,排序之后,输出特征点的坐标位置和特征值。
3 实验
多层次归并排序,一层的输出作为下一层的输入。通过乒乓操作形成流水操作。每一层的输出周期即为下一层的输入时间周期。所以总的时间周期分为两部分:每一层的输入时间周期和最后一层的输出时间周期。设总时间周期为T,第i层的输入时间为Ti,最后一层的输出周期数为T′。待排序队列长度为N,排序层数为M。

即并行归并排序时间复杂度为O(N)。优于传统的O(N lg(N))的归并排序。
系统首先使用ISIM仿真,验证结构正确性。然后在Xilinx Virtex5 SXT FPGA(XC5VSX50T-1ff1136)开发板上实现。KLT特征提取算法提取出4 096个特征点,设为1~4 096。要求从大到小排序。待排序的数据使用32位的整数,点的位置坐标X,Y使用10位。所以寄存器,或者FIFO内存储52位数据。FIFO的实现采用Xilinx提供的IP Core。
4 096个数据采用11层的结构,1到4层为基于寄存器的实现,5~11层为基于FIFO的实现。第11层不使用乒乓操作直接输出最终结果。排序部分结果如图5所示。
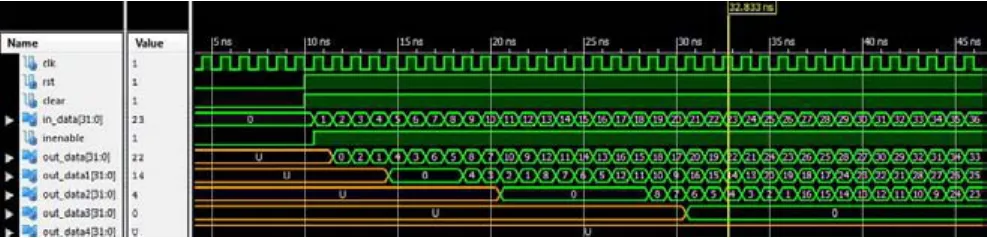
图5 仿真部分结果
表1和表2总结了本文的归并排序结构在Virtex5 SX50T开发板上的资源利用率。
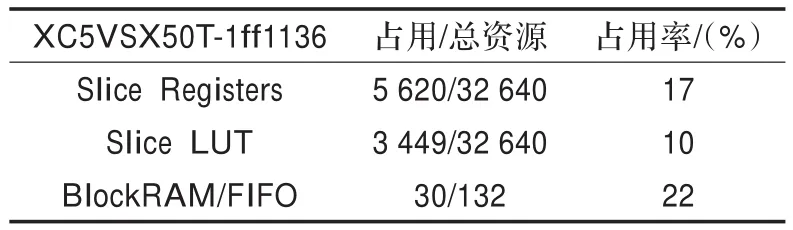
表1 综合归并排序的资源报告1

表2 综合归并排序的资源报告2
在对1 024×1 024的高清图片的特征点进行排序时,最高时钟频率可以达到159.795 MHz。即每秒可以处理100张以上分辨率为1 024×1 024的图片特征点排序。完全可以达到高清图片的实时处理要求。
4 结语
首先分析了经典的归并排序算法然后将其归并操作的结果和行为拓展到FPGA结构和硬件行为。提出了两种基于FPGA的归并操作,分别是基于寄存器的归并操作和基于FIFO的归并操作。两种操作都可以采用乒乓操作实现排序的完全流水。其中基于寄存器的结构采用时序逻辑。基于FIFO的结构采用时序逻辑和组合逻辑。最后在FPGA的归并操作基础之上,采用多层次构架,可以灵活地选用不同的归并组件,实现资源和效率的最大化。实验结果证明本文的归并排序完全可以满足高清图片KLT跟踪算法的实时排序。
[1]Lucas B D,Kanade T.An iterative image registration technique with an application to stereo vision[C]//International Joint Conference on Artificial Intelligence,1981:674-679.
[2]Tomasi C,Kanade T.Detection and tracking of point features,CMU-CS-91-132[R].Pittsburgh,PA:Carnegie Mellon University,1991.
[3]Shi Jianbo,Tomasi C.Good features to track[C]//IEEE Conference on Computer Vision and Pattern Recognition,1994:593-600.
[4]Birchfield S.Derivation of Kanade-Lucas-Tomasi tracking equation[Z].1997.
[5]Knuth D E.The art of computer programming,Vol.3-sorting and searching[M].[S.l.]:Addison Wesley,1973.
[6]Mart J,Cumplido R R,Feregrino C.An FPGA-based parallel sorting architecture for the Burrows Wheeler transform[C]//Proceedings International Conference on Reconfigurable Computing and FPGAs,Puebla City,Mexico,2005:28-30.
[7]Zhang Y,Zheng S Q.An efficient parallel VLSI sorting architecture[J].VLSI Design,2000,11:137-147.
[8]Parhami B,Kwai D M.Data-driven control scheme for linear arrays:application to a stable insertion sorter[J]. IEEE Trans on Parallel and Distributed Systems,1999,10(1):23-28.
[9]Ratnayake K,Amer A.An FPGA architecture of stablesorting on a large data volume:application to video signals[C]//41st Annual Conf on Information Sciences and Systems(CISS’07),2007.
[10]Edahiro M.Parallelizing fundamental algorithms such as sorting on multi-core processors for EDA acceleration[C]// Asia and South Pacific Design Automation Conference(ASP-DAC’2009),2009.
[11]吴彦宏,陈相宁.QoS保障机制中的FPGA堆排序实现[J].计算机工程,2009,35(12):223-225.
CHAI Zhilei,FANG Wanyuan
Development Center of Internet of Things Engineering,MoE,Jiangnan University,Wuxi,Jiangsu 214122,China
The Kanade-Lucas-Tomasi feature tracker(KLT)has
special attention due to its effectiveness on image track.The sort of feature point is the key point of joining the feature detection and feature track.This paper presents a novel FPGA-based parallel merge sort architecture for the KLT feature points,then analyzes its time period.The time complexity of the parallel merge sort architecture isO(N).The result shows that the FPGA-based merge sort can solve the real-time KLT feature points sort problem for HD image/video resolution.
parallel merge sort;Kanade-Lucas-Tomasi(KLT);Field Programmable Gate Array(FPGA)sort
A
TP391
10.3778/j.issn.1002-8331.1211-0179
CHAI Zhilei,FANG Wanyuan.FPGA-based multi-level parallel merge sorting architecture for KLT feature points. Computer Engineering and Applications,2014,50(21):157-161.
国家自然科学基金(No.60703106,No.61170121,No.61202312)。
柴志雷(1975—),男,副教授,研究生导师,主要研究方向:嵌入式系统;方万元(1988—),男,硕士研究生,主要研究方向:视频压缩、图像处理。E-mail:zlchai@jiangnan.edu.cn
2012-11-15
2013-03-11
1002-8331(2014)21-0157-05
CNKI出版日期:2013-09-05,http://www.cnki.net/kcms/detail/11.2127.TP.20130905.1048.006.html

