热光二阶关联的影响因素实验研究

田 甲，林海龙，高 禄

(中国地质大学(北京) 数理学院，北京 100083)

1 引 言

1956年，汉勃雷-布朗(R. H. Brown)和特威斯(R. Q. Twiss)为测量恒星角直径而设计著名的实验[1]，后来人们就以他们的名字命名该实验为“HBT”实验. HBT实验第一次证实了光的强度关联效应, 实验本身也成为测量强度关联的典型方法,在量子光学发展史上具有里程碑的意义. 1995年,美国马里兰大学的Yanhua Shih等人利用自发参量下转换的纠缠光子对完成了奇特的成像实验——鬼成像(ghost imaging)[2],此实验使得在没有物体的闲散光路中获得物体的空间信息成为了可能. 当时人们认为这是一种量子现象,只有采用纠缠双光源才能实现鬼成像. 2002年, Rochester大学的Boyd等人巧妙地利用随机旋转的反射镜反射激光获得了空间频率随机分布的热光源,通过光场的强度测量获得了透射物体的鬼成像[3]. 该实验结果表明鬼成像实验也可以利用经典光源实现，而并非是量子光源所特有的现象. 这一实验报道更是引起了科学界的一场争辩：鬼成像实验是否是一种量子现象？ 随后，国内外很多研究组在热光二阶关联测量方面开展了理论和实验研究工作[4-7]. 研究结果表明热光源可以模仿纠缠双光子源实现鬼干涉、鬼成像等双光子关联测量实验.

在研究热光二阶关联特性的实验中，HBT测量是一个必要的实验基础，因此对于HBT影响因素的研究极为关键. 本实验中，采用激光照射旋转毛玻璃形成空间频率随机分布的热光源，通过改变热光源的横向尺寸及物光和参考光光程差，研究光源特性及光路设计对热光二阶关联的影响.

2 实验原理

HBT的实验原理如图1所示. 非相干热光源发出的光被非偏振分束器分成2束，分别自由传递到达探测器D1和D2. 将其中一个探测器探测面上某一固定点的光强值与另一个探测器探测面上各个点的光强值进行强度关联测量，即可获得HBT值.

图1 HBT实验原理图

根据高斯矩定理,满足高斯统计分布光场的高阶关联可以用一阶关联函数表示，则热光场的二阶关联函数可以表示为

(1)

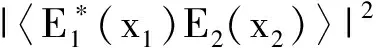
光场从光源横截面到探测器的探测面自由传播的脉冲响应函数可以表示为

(2)

其中k=2π/λ为光场的波数，z是从光源横截面到探测器的探测面的距离，xj和x0分别表示探测面和光源横截面的空间横向坐标. 在近轴近似条件下，式(2)可以写为

(3)

假设理想情况下，热光源发出的光具有无穷小的相干长度，热光源横截面的一阶关联函数可以表示为

〈E0(x)E0(x′)〉=S0δ(x0-x0′) ,

(4)

这里假设光场强度分布为常量S0. 将式(3)和(4)代入到式(1)中的关联项，可以得到光场的一阶互关联函数为

(5)

其中r为光源发光面的尺寸半径. 于是，可以得到HBT实验的二阶关联函数为

(6)

固定一个探测器，扫描另一个探测器就可以得到

(7)

式(7)表示非相干热光源HBT实验测得的二阶关联函数形式，其归一化形式可以表示为

(8)

从式(8)中可以看到，归一化HBT曲线的半高宽与光源距探测面的距离z、光源的尺寸r及波长λ有关. HBT曲线的半高宽随着z的增加而增大，随r的增加而减小. HBT理论曲线如图2所示.

图2 HBT理论曲线图

3 实验研究

3.1 实验装置

实验光路如图3所示. 波长为632.8 nm的激光器发出的激光经过平面镜M反射，依次通过偏振片P1和P2，它们的作用是保证光源为线偏振光，同时可以组合调节光强. 扩束透镜N可以调整激光光斑的大小. 经扩束后的激光照射在转动的毛玻璃G上形成空间频率随机分布的赝热光源. P3为放置在热光源附近的光阑，用来调节热光源的横向尺寸. BS为50/50非偏振分束器，可以把光源发出的光束分为2束，2束光分别自由传递到达探测器D1和D2的探测面. 两探测器的探测面距离热光源G的距离分别为d1和d2. 2个探测器分别连接计算机中采集卡的端口，由相应的采集程序进行数据采集和测量，并将数据存储到计算机中.

图3 HBT实验装置图

依据HBT原理，本实验所采用的采集方式为：取探测器D1探测面上某一固定点值与另一个探测器D2探测面上的各个点的光强值进行关联测量，对采集到的数据进行归一化关联计算，从而得到光场的二阶关联HBT值.

3.2 实验过程及结果

首先,固定光阑P3的直径为3 mm，通过改变探测器D2距离光源的光程，改变物光和参考光两光路的光程差，测量相应的HBT值. 探测器D1保持位置不变，距离分束器BS的距离为d1=31.80 cm,探测器D2的位置依次变化使光程差分别为Δd=d2-d1=0,5,10,20 cm. 实验结果如图4所示. 当Δd=0 cm时，归一化的HBT值达到了1.935，接近理想值2;随着探测器到光源光程差的增加，HBT值逐渐减小. 当光程差Δd达到20 cm时，二阶关联的HBT值减到1.221，二阶关联值变得较低. 实验结果表明：热光二阶关联随着2个光路光程差的增大而下降，同时曲线的半高宽也随之增大，导致二阶关联测量的分辨率降低. 所以在上述热光二阶关联实验测量系统中，在光源尺寸是直径为1 mm的圆形区域情况下，物光和参考光两光路的光程差不能大于20 cm,否则二阶关联特性将消失.

图4 HBT值随光程差变化曲线

其次，固定探测器D1和D2的位置，即d1=d2=31.80 cm. 通过改变光阑P3的直径即热光源的横向尺寸，测量相应的HBT值. 实验测量结果如图5所示. 实验结果表明：当光阑直径为1 mm时，关联值达到1.797；随着光阑直径的增大，HBT值逐渐减小，当直径增加到10 mm时，二阶关联值下降到1.361. 由此可见，强度关联值随着热光源横截面尺寸的增大而降低. 同时，HBT曲线的半高全宽随着光阑直径的增加而减小，这说明热光二阶关联测量系统的分辨率随着光阑直径的增加而提高.

图5 HBT值随光阑直径变化曲线

4 结 论

热光的归一化二阶关联HBT值与物光和参考光光程差及光源的横截面尺寸有紧密联系. 研究结果表明：随着热光二阶关联测量系统中物光和参考光光程差增加，HBT值会随之降低，而且曲线的半高全宽也随之增加，导致系统的测量分辨率降低. 随着光源横截面尺寸增加，即实验装置中光阑P3直径增大，HBT值也会随之降低，但是曲线的半高全宽却随之减小，系统的测量分辨率提高. 这说明尽管光源横截面尺寸的增加可以提高热光关联系统的测量分辨率，但是要以降低图像可见度为代价.

参考文献：

[1] Brown R H, Twiss R Q. Correlation between photons in two coherent beams of light [J]. Nature, 1956,177:27-29.

[2] Pittman T B, Shih Y H, Strekalov D V, et al. Optical imaging by means of two-photon quantum entanglemen [J]. Phys. Rev. A, 1995,52:R3429-R3432.

[3] Bennink R S, Bentley S J, Boyd R W. “Two-photon” coincidence imaging with aclassical source [J]. Phys. Rev. Lett., 2002,89(11):113601-1-4.

[4] Cao De-zhong, Wang Kai-ge. Sub-wavelength Interference in macroscopic observation [J]. Phys. Lett. A, 2004,333:23-29.

[5] GAO Lu, XIONG Jun, ZHANG Shu-heng, et al. Improving visibility of diffraction pattern with pseudo-thermal light [J]. Chin. Phus. Lett. , 2008,25(4):1277.

[6] 李璐，关东石，刘宏超，等. 光的偏振性对Hanbury Browm-Twiss实验的影响[J]. 量子光学学报，2009(3):201-206.

[7] 高禄，张颖涛，汪凯戈. 相位物体的热光关联成像[A]. 第十二届全国量子光学学术会议论文集[C]. 南昌：2006.