橡皮筋热缩性质的定量表示及应用

孙楚旻

(北京师范大学 物理学系，北京 100875)

1 橡皮筋的热缩现象

生活中可以观察到橡皮筋具有受热收缩的性质. 通过以下实验可以简单地演示该现象：橡皮筋上端固定，下端悬挂1把普通剪刀，可以在剪刀上加重物使橡皮筋处于较明显的伸长状态. 调整橡皮筋上端的固定点的高度，使剪刀的下端恰好触碰到某一水平面. 用普通家用电吹风加热橡皮筋，可以观察到加热后剪刀刀尖脱离原来所在的平面，即橡皮筋受热收缩(图1) .

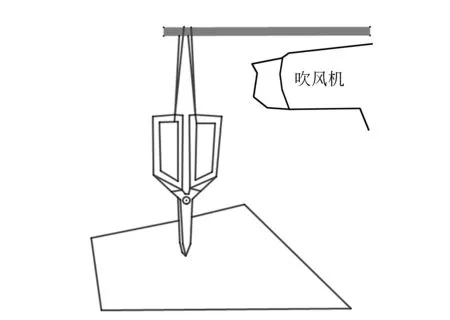
图1 橡皮筋热缩性质的定性演示实验

由上面实验结果可以得知，如果让橡皮筋保持定长，橡皮筋上所受外力将随着温度升高而增大. 以下的理论将解释这一现象的成因，而实验可以定量研究这一现象. 数据分析结果符合理论分析.

2 原 理

利用热力学知识可以解释橡皮筋受热收缩的原因. 通常说来，假定橡皮筋试样在等温下受到拉伸力f，试样被拉长了dl，外界对试样所作的功为fdl[1]. 因为拉伸过程中橡胶体积不变，对于等温可逆过程有

dU=TdS+fdl,

(1)

其中U是试样的内能，T是外界温度. (1)式可改写成

(2)

另外，根据Gibbs自由能的定义

F=H-TS=U+pV-TS,

(3)

所以有

dF=dU+pdV+Vdp-TdS-SdT.

(4)

对于橡胶弹性体来说，在拉伸过程中体积不变，而且实验是在恒压下进行的，故

dF=fdl-SdT.

(5)

从(5)式可得

(6)

则

(7)

因此(2)式可以改写成

(8)

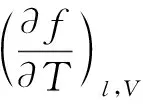
忽略Gibbs自由能和Helmholz自由能的区别，有

F=U-TS.

(9)

熵力是指一个系统中的一种宏观作用力，表现为整个系统对于熵增加的统计趋势. 定义熵力为自由能对于长度的偏导数[2-3]，则

(10)

因此，橡皮筋处于平衡态时，其熵力与外力大小相等，方向相反.

3 实 验

3.1 测量温度场实验

实验采用的热源是400 W的NSB-80小金鱼取暖器，其中热源部分是1根石英管(约19 cm). 电子温度计为实验室常用的长管水银温度计，量程是20～100 ℃，精度为1 ℃. 固定温度计尖端对准取暖器灯管中心以及中心外其他点，测得温度计示数近似相等. 用游标卡尺测量温度计针尖到取暖器铁丝网的不同距离，读出温度计在此距离的示数，多次测量取平均值，得到距取暖器铁丝网的距离与温度的关系. 对上述关系作出最小二乘法光滑函数拟合之后，可以计算距取暖器铁丝网的一段距离处的温度近似值.

3.2 橡皮筋热缩性质的定量表示

假设橡皮筋在某一温度下放置一段时间以后达到热平衡状态，此时橡皮筋熵力大小与所受外力大小相同. 可以通过电子秤测量橡皮筋所受的外力的大小，即熵力的大小，并用温度场拟合的结果得出橡皮筋定长时熵力与温度的关系.

实验装置如图2所示. 铁架台上固定不易形变的刚性杆，将橡皮筋上端套在杆上，下端悬挂能使其伸长的重物，如砝码. 实验时注意取暖器灯管与拉长的橡皮筋平行(图3). 用游标卡尺控制刚性杆到橡皮筋下端的距离为定长L(图4).

待灯泡温度场较稳定且电子秤示数也较稳定后再读数，并多次读数取平均值.

将电子秤的示数转化为橡皮筋的熵力的方法是：先用电子秤测出砝码和橡皮筋的总质量M，再将橡皮筋上端套在刚性杆上，测出室温下橡皮筋定长时橡皮筋与砝码的总质量M′，先调零电子

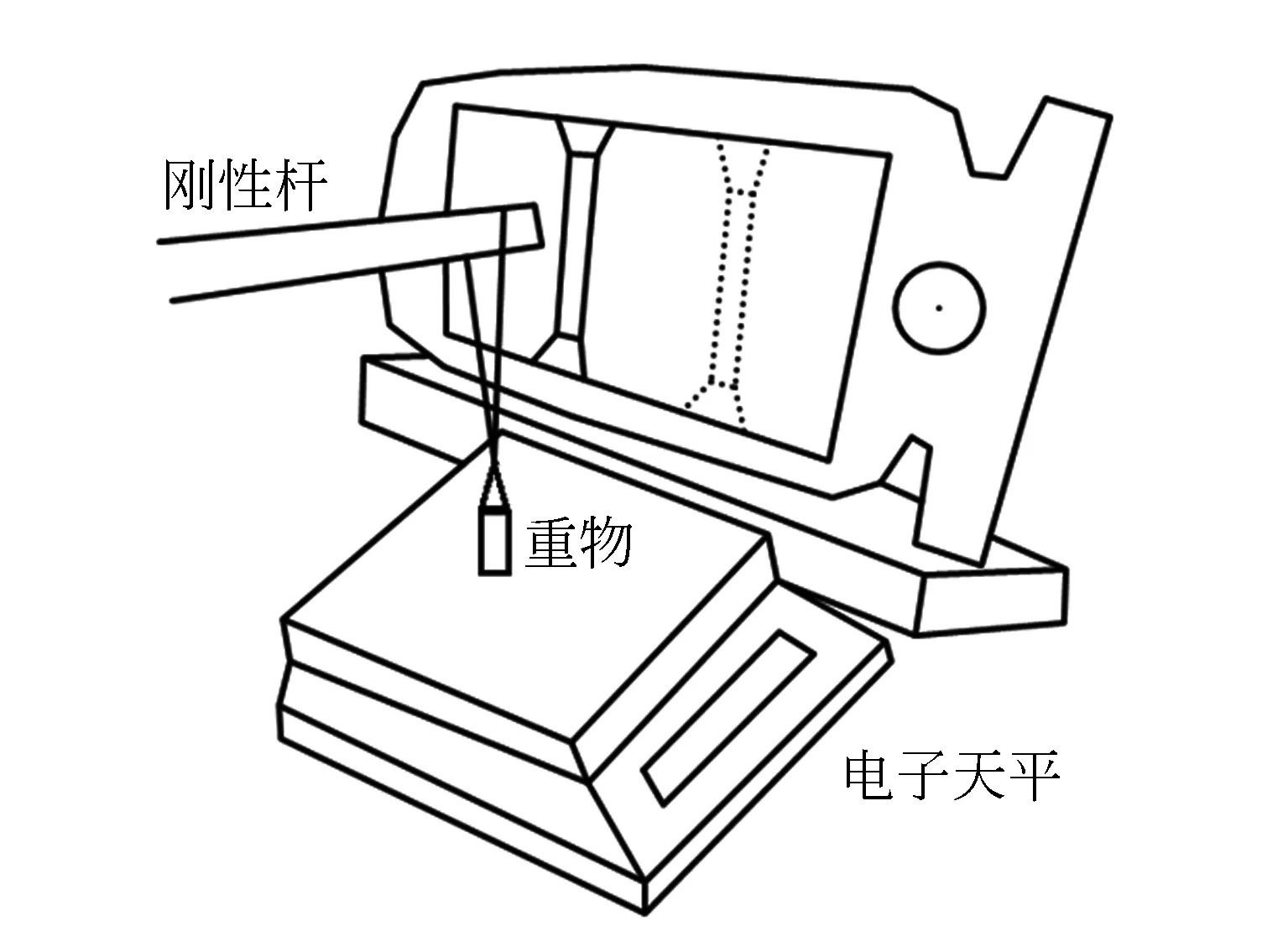
图2 定量测量橡皮筋热缩性质的实验装置

图3 取暖器灯管与拉长的橡皮筋平行

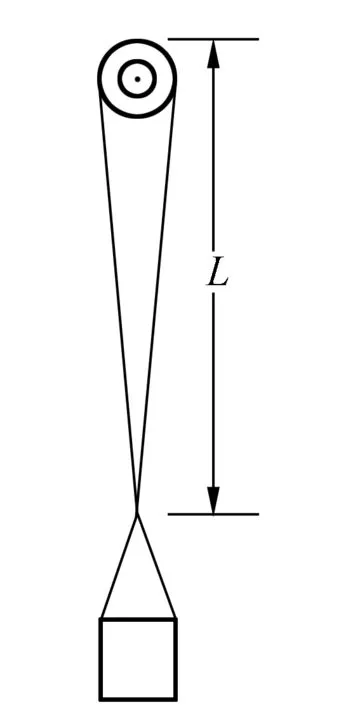
图4 橡皮筋定长

秤，设在实验加热过程中，电子秤的读数变为m. 则橡皮筋在某一温度下所受的熵力大小为

fa=[m+(M-M′)]g.

(11)

取该纬度重力加速度大小为g=9.809 0 m/s2.

假设此时的温度即上一实验中得到的拟合温度场的温度,这样，可以作出一系列不同定长时的熵力与温度曲线.

4 数据分析

4.1 温度场测量实验

直接测量的温度数据如表1所示.

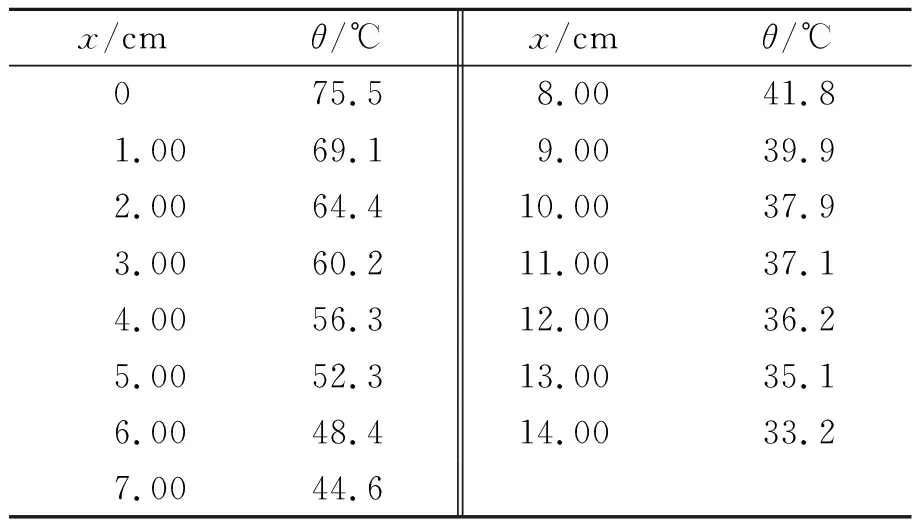
表1 温度场测量数据

用最小二乘法拟合得到的温度场曲线如图5所示，温度场函数是四次函数，R2=0.999. 根据这一拟合结果可计算出距取暖器铁丝网不同距离的温度.

图5 温度场原始数据的拟合曲线

4.2 橡皮筋热缩性质的定量表示

首先用3种不同的橡皮筋做定长时熵力大小与温度的关系实验. 分析数据发现线性拟合结果良好且截距均为正数，验证了橡皮筋的热力学理论，即构象熵对长度的偏导数与温度无关，而内能对长度的偏导数是正值.

取热缩现象较为明显的橡皮筋，研究其不同长度时熵力与温度的关系，结果如图6所示.

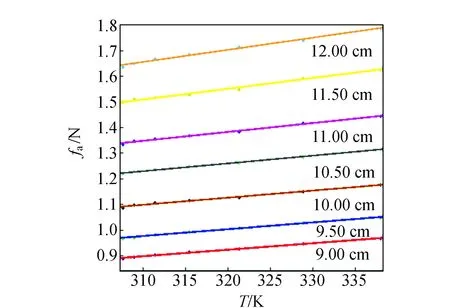
图6 橡皮筋不同长度时熵力与温度的关系

4.3 橡皮筋不同长度时其熵对长度的偏导数和内能对长度的偏导数与长度的关系

取橡皮筋不同长度时熵力与温度关系的斜率，即橡皮筋构象熵对长度的导数，做出熵力随长度关系的变化如图7所示.

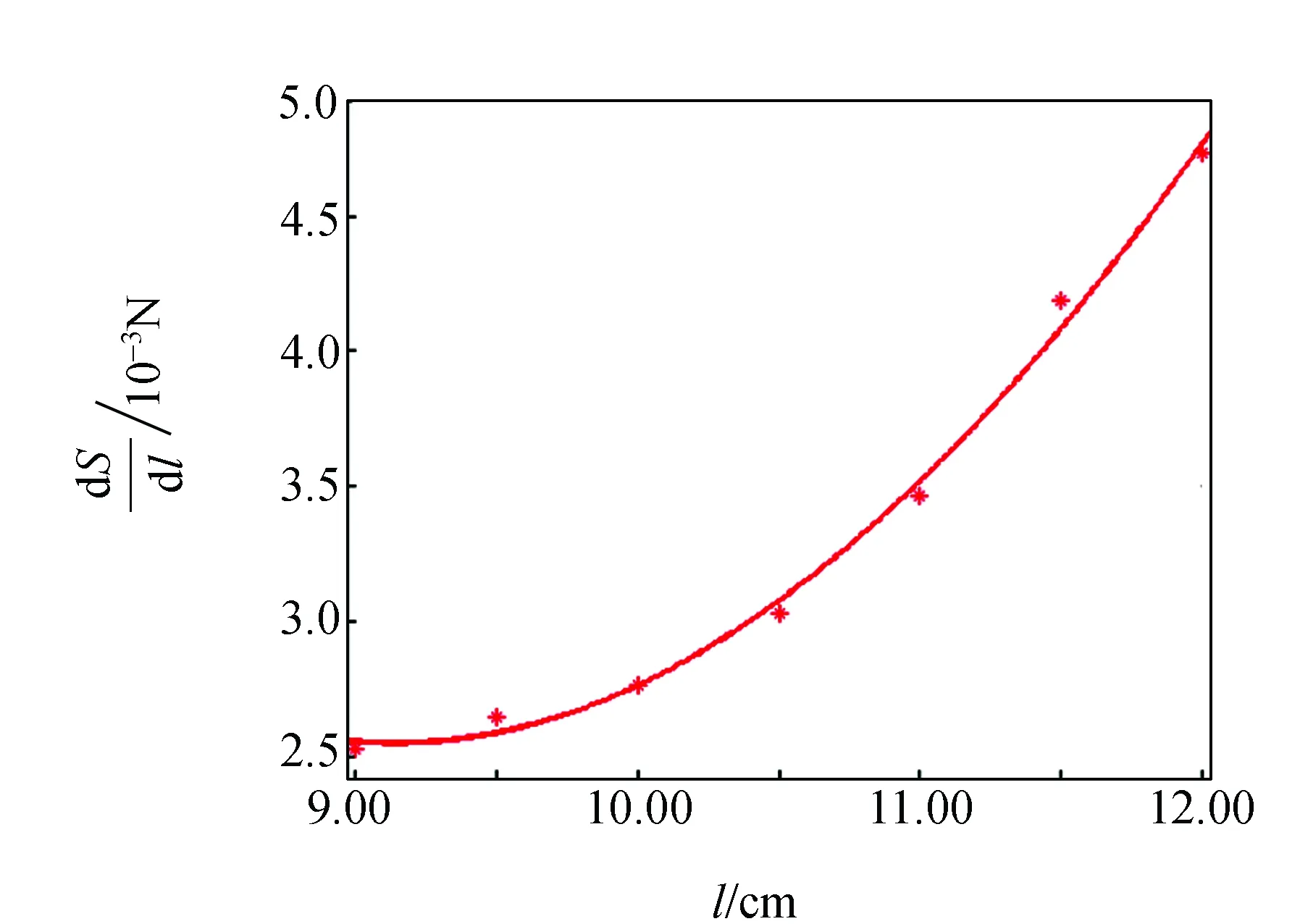
图7 熵对长度的偏导数与橡皮筋长度的关系

分析数据得出橡皮筋构象熵对长度的导数随长度的增加而增加，且三次函数拟合R2=0.994 9，而橡皮筋内能对长度的导数(即截距)是正值，它随着长度增加的变化不定，其中可能有实验误差原因，也可能是事实如此，理论分析有待进一步探讨.

4.4 常温下不同长度时构象熵和内能对橡皮筋弹力的贡献比例

利用拟合温度场数据以及定长时橡皮筋熵力与温度关系的数据，可以分析一定温度范围内不同长度时构象熵和内能对熵力的贡献比例.

计算20 ℃时2部分对橡皮筋弹力的贡献比例，如图8所示. 这组数据中由内能引起的橡皮筋弹力的百分比的平均值是17.953%；由构象熵变化引起的橡皮筋弹力的百分比的平均值是82.047%. Folry测量了内能对橡皮筋弹性的贡献,约为11%～18%[4]. 实验在精度范围内给出的数据大致与这一结果相符.由此可见常温下橡皮筋的弹力主要由构象熵引起. 可以推断一定温度下构象熵对橡皮筋弹力的贡献比例远大于内能对弹力的贡献比例.

图8 常温下橡皮筋不同长度时构象熵和内能对橡皮筋弹力的贡献

5 应 用

利用橡皮筋的热缩性质制作橡皮筋热机[5]，实验装置图如图9所示. 转轮由长度为89.50 cm的铁丝围成的圆环(直径28.00 cm)，芯盘为1根长铁丝穿过直径为8.00 cm的小圆盘，在圆环与圆盘之间盘上有88根橡皮筋辐条，成品架于支架上，在其一侧固定加热灯或取暖器[图10(a)].

图9 橡皮筋热机实验装置图

图10 橡皮筋热机原理图

该装置的原理为：加热热机一侧，橡皮筋产生热缩现象[图10(b)]，造成圆环重心的偏移产生重力矩，最后导致圆环转动. 热机转动一定角度后，由于力矩的变化及橡皮筋散热恢复原长，转动停止.一段时间后，由于热缩热机又继续转动，如此即为所谓的“走走停停现象”.

5.1 关于转动平均速率的测量及优化

测量一定时间内热机转动的角度，除以所用时间，得出的平均速率即为转动平均速率ω. 为了优化这一属性，对热机光照角度进行了优化.

如图11所示，受热区中心点与水平方向所成角度称为光照角度α. 可以通过测量热机不同光照角度下10次转动的角度φ和与转动所需时间t的关系来确定最佳的光照角度，测量结果如表2所示.

(a) (b) (c)图11 橡皮筋热机光照角度优化

α/(°)φ/(°)t/sω/[(°)·s-1]-306332043.10-204741752.71-104232032.0803511801.94102841631.74202171921.13301791840.97

当光照角度为-40°时，热机由于阻力矩过大的原因几乎无法转动. 由表1得出结论：当光照角度为-30°左右时热机平均转动速率最大.

关于负角度平均转动速率普遍比较大的理论解释为：开始时虽然所受重力力矩比0°时的力矩小，但是随着转动的继续，重力力矩会经历逐渐增大到逐渐减小的过程，作用时间也较长. 而0°及正角度动力矩在逐渐减小，所以负角度时平均转动速率也较大.

5.2 关于转动顺畅度的测量及优化

热机多次受热放热后单次转动角度会逐渐稳定在一定的角度范围内. 所谓转动顺畅度，即多次受热后热机单次能转过的平均角度，也是能反映热机性能的重要指标. 同样对其光照角度进行优化，图12为热机在不同光照角度下转动角度φ与转动次数N之间的关系.

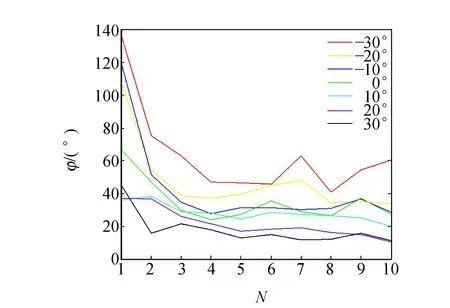
图12 热机在不同光照角度下转动角度φ与转动次数N的关系

同样可以得出光照角度为-30°左右时热机转动最为顺畅.

6 结束语

这一组实验验证了关于橡皮筋的热学知识，定量表示热缩物质的性质，开发了适合普通物理实验教学的创新性实验，对于帮助学生直观地理解相应的热力学理论很有意义. 橡皮筋的热缩性质可以应用于诸如橡皮筋热机等演示仪器，方便此性质的演示及实验教学，但因其机械效率低下(低于1%)限制了其应用发展. 进一步拓展关于橡皮筋的热力学实验，可以思考如何测量宏观意义上柔软且热缩物体的线胀系数，橡皮筋状态方程的验证，等等.

参考文献：

[1] 何曼君,陈维孝,董西侠，等. 高分子物理[M]. 上海：复旦大学出版社，1990:221-223.

[2] 周江玥. 橡胶带热机原理及制作[D]. 北京：北京师范大学，2005:1-3.

[3] 朱平平. 高聚物的高弹性[D]. 合肥：中国科学技术大学,2005:2-3.

[4] Marx G， Ogborn J， Tasnadi P. Rubber as a medium for teaching thermodynamics [J]. Eur. J. Phys., 1984,5:232-233.

[5] 粟岳，李晋，刘德华. 橡皮筋热机的设计和制作[J]. 周口师范高等专科学校学报，1999，16(5)：82-85.