复杂介质的土坝渗流计算分析

，，

(1.河南灵捷水利勘测设计研究有限公司,河南 南阳 473000;2.南阳市水利建筑勘测设计院,河南 南阳 473000)

复杂介质的土坝渗流计算分析

杜跃亭1，贾鹏生2，张丽丽1

(1.河南灵捷水利勘测设计研究有限公司,河南 南阳 473000;2.南阳市水利建筑勘测设计院,河南 南阳 473000)

在早期修建的土石坝水利工程中，由于地质勘查相对落后，不能准确查清坝基地质条件，加上施工过程中取材有差异，导致坝体、坝基局部相邻介质的渗透性相差较大。常规的渗流计算方法得到的渗流计算结果不合理，通过增设渗流过渡区域的手段，降低相邻介质渗透系数偏差，较好地解决了复杂介质的渗流计算问题。

复杂介质；土石坝;渗流分析

早期的土石坝，大多为“三边”工程，加之当时的地质勘察技术相对落后，不能很清楚地探明坝址区域内的地层情况，导致很多坝基未清理至发育较好的岩层、土层即开始筑坝，或者直接对山体进行削坡后即作为坝体的一部分。另外，由于早期施工过程中，取材有差异，导致坝体材料非常复杂，相邻的两层介质渗透性可能相差1～4个量级。由于早期水库运行水位较低，渗流问题不是很明显，然而随着经济社会的发展，用水需求日益增大，这类水库的渗流问题逐渐凸显。

针对这一问题的渗流场数值分析，目前较多采用各向同性渗流理论或沿坐标轴的各向异性理论进行分析[1，2]。常规的分析结果表明：相邻两层介质的渗透系数比值小于103数量级时，可以直接进行计算，否则将出现错误的结果或迭代不收敛问题[3]。

为了避免出现相邻介质层渗透系数相差较大的情况，可通过设置过渡区域的手段加以解决。基于渗流有限元分析的基本原理, 利用Geo-studio中的SEEP /W 模块[4],模拟坝体渗流情况。

1 计算方法

1.1 有限元计算原理

对土坝的渗透分析采用基于有限元法的SEEP/W进行，通过赋予材料特性和边界条件，求得土体内部的渗流场和渗透力分布情况，分析最可能发生破坏的位置。

有限元渗流分析时水体在土体内部的流动方程符合达西规律，根据是否考虑时间效应，将计算分析划分为稳态和瞬态两种情况。稳态为理想状态，不考虑时间和初始内部体积含水量变化的影响，流体的运动方程见式(1)，实际上这种理想状态在入渗过程中很难达到。瞬态分析考虑了时间作用，用以分析库水位变化时入渗过程中水位及浸润线等随时间的变化过程，流体运动方程见式(2)，当计算时间足够长时，瞬态分析结果接近稳态分析结果。

稳态方程：

(1)

瞬态方程：

(2)

上二式中H——总水头；

kx、ky——x、y方向的渗透系数；

q——边界流量；

θ——体积含水量；

t——时间。

有限元软件SEEP/W材料本构中引入非饱和土特性，程序中反映非饱和材料特性的参数有：土体的渗透系数、基质吸力、土体体积含水量等；其中非饱和土体的渗透系数是土体体积含水量和基质吸力的函数[5]，土体体积含水量的变化受到土体应力状态和土性的影响，土体应力状态主要由(σ-ua)和(ua-uw)控制(其中：σ1土体总应力，在渗透分析中保持不变；ua为孔隙气压力)[6]，假定孔隙气压力在渗流分析中也保持恒定，则土体体积含水量只与ua-uw有关，体积含水量与时间的关系可由式(3)表示：

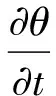
(3)

式中mw——由负孔隙水压力引起的体积变化系数，为土水特征曲线斜率。

将式(3)代入式(2)得到非饱和土体的流体运动方程：

(4)

1.2 过渡区域渗透系数及厚度的确定

由于过渡区域的渗透性和两种介质都有关系，同时也为防止因两种介质渗透性差异过大导致模型求解不收敛问题，采用下式确定过渡区域的渗透系数[3]：

(5)

式中k——过渡区域的渗透系数；

k1、k2——相邻介质1、2的渗透系数。

过渡带的厚度根据单元尺寸取0.5m。

2 工程概况

南阳西部某水库于1968年10月开工兴建，水库控制流域面积58km2,总库容2447万m3，工程等别为Ⅲ等，主要建筑物级别为3级。洪水标准为1000年一遇校核，校核洪水位258.65m(黄海高程系,下同)，相应库容2182万m3；50年一遇设计，设计洪水位257.12m，相应库容1973万m3；兴利水位253.20m，兴利库容1250万m3。主坝为黏土均质坝，坝顶高程261.30m，坝长630m，最大坝高36.3m。目前，该水库是一座以防洪、灌溉为主，兼顾发电、养鱼等综合利用的水利枢纽工程。

该水库大坝左台地段原为一条很厚的土丘岭，修建水库时在左台地上、下游取土，并按照设计坝坡坡度将天然土丘岭进行削坡，最终形成类似坝体形式的坝基(根据工程实际，为了便于模型建立和渗流分析计算，简化为坝体进行分析)。坝体材料自上而下依次为：坝体填土、泥质中砂、粉质壤土、泥质砂砾石(详见图1)。

坝体填土厚15.8～18.3m,黄褐、棕褐色，填土性质较复杂，以含砾重粉质壤土、含砾粉质黏土为主，含风化石渣、砾石及砂粒，分布不均匀。泥质中砂以透镜体形式分布于241.90～244.50m高程，层厚0.8～4.2m, 渗透系数4.65×10-5m/s，强透水层，局部贯通形成渗漏通道。粉质壤土层厚9.7～14.0m，含少量砾石、砂粒，砂粒分布不均匀。泥质砂砾石层顶高程229.1～234.1m,层厚2.0～7.3m，渗透系数9.2×10-4m/s，强透水层，泥质含量21.4%，砂粒含量50.4%，卵、砾石含量28.2%，卵石粒径5～10cm，成分以灰白色砂砾岩为主。

由于水库除险加固前一直为低水位运行，未形成渗流破坏。近年来随着水资源日益紧缺，工程除险加固后，水库开始长期高水位运行，强透水层渗流问题逐渐显现，水位在254.60m时，散浸面积达780m2，水位在250.00m时，散浸面积也有150m2。为此，设计采取塑性混凝土防渗墙工程措施来进行除险加固。

图1 最大坝高断面地层分布

3 计算模型及参数

结合土石坝坝址区地形地质条件,以坝段最大坝高剖面为对象,建立平面有限元计算模型，采用 3节点和4节点平面等参单元对坝体及坝基划分单元,单元总数8951个, 节点总数9165个,二维有限元模型见图2。各分区材料的渗透系数见下表。

图2 SEEP/W单元网格模型

坝体及过渡区域材料渗透系数表

4 计算成果及分析

本文仅选取正常水位工况下坝体渗流场的计算结果进行分析，计算结果见图3、图4。

图3 未设置渗流过渡区域渗流场分布 单位：m

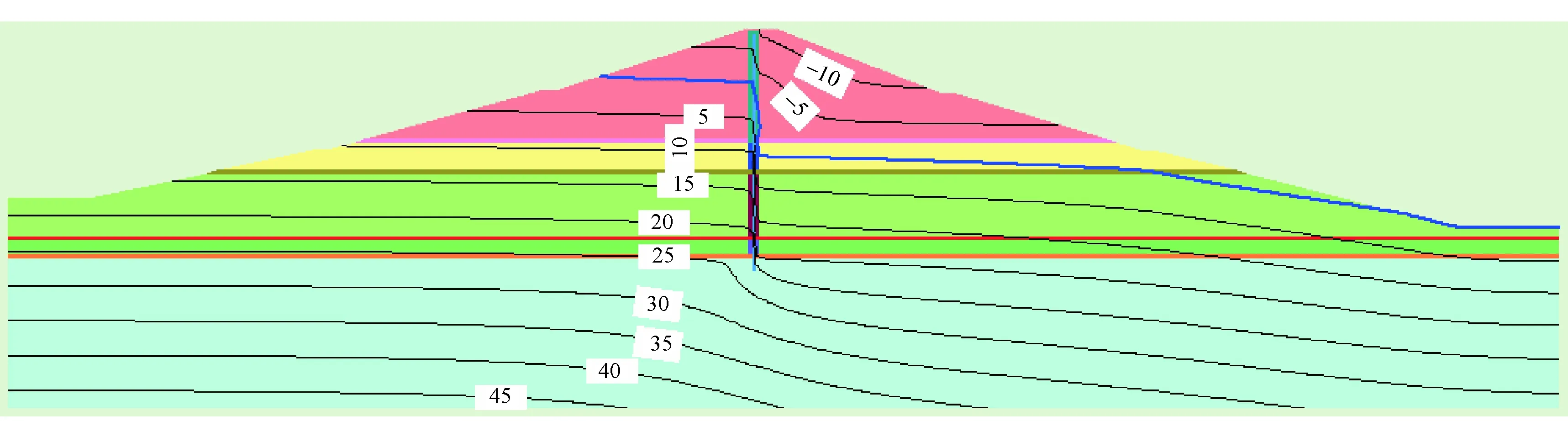
图4 设置渗流过渡区域渗流场分布 单位：m

由图3、图4正常水位工况下坝体坝基的渗流场可以发现，当坝体未设置渗流过渡区域时，浸润线经塑性混凝土心墙时折减较小，坝体浸润线呈不规则分布，背水坡中部出现封闭的渗流场，且出现二次逸出的现象，出现该种情况的原因是相邻两层介质的渗透系数太大，导致有限元计算时形成的渗透系数矩阵出现奇异。当坝体设置渗流过渡区域时，可以看出浸润线经塑性混凝土心墙时折减较大，渗流场分布合理，浸润线呈光滑渐变，逸出点位置合理，说明增设渗流过渡区域可以较好地解决相邻介质渗透系数相差较大的渗流计算问题。另外，通过在坝体设置的浸润观测管观测数据，其形成的浸润线与增设过渡区域后的渗流计算结果接近，这也进一步说明本文的结果是合理的。

5 结 语

早期修建的土石坝，地质勘查技术相对落后，未准确查清地质情况即开始筑坝，导致清基不彻底，坝体比较复杂，相邻介质的渗透性相差较大，常规的渗流计算方法得到的渗流计算结果大多不合理甚至错误。本文通过在渗透性相差较大的相邻介质中间增设渗流过渡区域的手段，降低相邻介质渗透系数偏差，较好地解决了复杂介质的渗流计算问题。

[1]Brunone B.，Romano N.，Santini A.Numerical Simulations of one-dimensional infiltration into layered soils with Richards equation using different estimates of the interlayer conductivity [J].Vadose Zone Journal，2003(2): 193-200.

[2]Lima-Vivancos V.，Voller V.R.Two numerical methods for modeling variably saturated flow in layered Media [J].Vadose Zone Journal，2004(3): 1031-1037.

[3]刘昌军,丁留谦,宁保辉,张顺福.心墙土石坝渗流场的无单元法模拟[J]. 水力发电学报，2012(3).

[4]Fredlund D G， Rahardjo H.Soil Mechanics for Unsaturated Soils[M].New York:Wiley,1993.

[5]Fredlund D G， Morgenstern N R. Constitutive relations for volume change in unsaturated soils [J]. Can Geotech J.,1976(13)：261-276.

CalculationAnalysisofEarthDamSeepageinComplicatedMedium

DU Yue-ting1,JIA Peng-sheng2, ZHANG Li-li1

(1.HenanLingjieHydraulicInvestigationandDesignResearchInstituteCo.,Ltd.,Nanyang473000,China;

2.NanyangHydraulicBuildingInvestigationandDesignInstitute,Nanyang473000,China)

During early process of constructing earth and rock dam hydraulic project, geological condition on the foundation of the dam can not be found precisely due to geological investigation was relatively lagged behind, plus there was difference in using materials during the process of construction, causing greater differences of penetration in local neighbored medium in dam body and the foundation of dam. Seepage calculation result obtained from regular seepage calculation methodology is not reasonable, and seepage calculation issue of complicated medium can be better solved with means of adding seepage transition area and reducing deviation of penetration coefficient of neighbored medium.

complicated medium; earth and rock dam; seepage analysis

TV641

A

1673-8241(2014)09-0067-04