随机边界元法及其在水工结构可靠度分析中的应用研究

(中国水电顾问集团贵阳勘测设计研究院，贵阳 550081)

科学研究及工程设计

随机边界元法及其在水工结构可靠度分析中的应用研究

贾景伟

(中国水电顾问集团贵阳勘测设计研究院，贵阳 550081)

对于一些计算精度要求比较高、计算量比较小、结构比较复杂的施工结构，通常会使用边界元法进行计算，基于此，本文对随机边界元法及其在水工结构可靠度的分析运用进行了研究。

水工结构；随机边界元法；可靠度分析

材料加工时，在各种因素的影响下，工程结构的几何参数和空间位置会有一定的随机性，而且，外界条件和结构荷载也会随着时间和空间的变化出现变化。在电脑信息技术条件下，有效解决了工程施工中的荷载问题，而且在进行数学模型建模过程中，考虑了客观事物的随机性，更加重视问题性质，符合实际情况；在结构设计时，使用结构可靠度比较高的设计方法，解决了传统安全系数设计过程中存在的问题。

1 计算结构的可靠度

结构的功能函数主要是对结构的状态进行描述，可以使X=(X1，X2…,Xn)T这一随机变量表示为g(X)=g(X1，X2，…,Xn)，得出极限状态下的方程式g(X)=0，一般情况下，在功能函数中会包含一个用来对结构抗力和结构强度进行标示的随机变量R=R(X)=(R1，R2，…,RK)T,比如材料的断裂韧度、屈服极限、摩擦系数、疲劳强度、允许位移、黏聚力等，R作为X的显函数，以及一个用来对荷载效应进行标示的随机变量S=S(X)=(S1,S2,…SL)T,比如应力强度因子、应力、裂缝宽度、位移等，X的显函数为R,但是X的显式不能为S,这主要是因为荷载效应和荷载之间存在相互转换的关系，因此，可以使用如下功能函数进行表示：

Z=g(X)=g(R，S)

本文对结构的可靠性指标进行计算时，使用一次二阶矩法进行计算，计算时要对功能函数g在设计验算点x=(x1,x2,…,xn)T处X的偏导数进行考虑，通常没有办法得到g(X)的解析式，也就没有办法得到X偏导数的表达公式，根据复合函数的求导法则和公式可以得出如下矩阵形式：

在公式中Jacobi矩阵为

在计算结构可靠度时，由于结构功能函数一般只能使用荷载效应S显式和强度R进行标示，在实际工程应用中，利用数理统计只可以得到一个基本的随机变量的随机信息，为了可以使用一次二阶矩法对β进行计算，需要将设计验算点X处S=S(X)和R=R(X)值，以及Js值和JR值，一般X处的JR值和R值都可以很容易得到，而Js值和S需要使用数值计算法进行计算，本文使用随机边界元法对X处的Js值和S值进行计算[1]。

2 随机边界元法在水工结构可靠分析中的运用

在使用随机边界法编制程序时，方程求解和结构边界离散方面的处理方法和边界元法是一致的，本文以混凝土重力坝为实际案例进行探讨。

通常设计混凝土重力坝的时候，需要考虑稳定破坏和强度破坏两个方面，对于重力坝的可靠度主要包含了温度可靠度和强度可靠度，本文只对重力坝满库运行时正常荷载下的可靠度进行考虑，根据Mohr应力圆和Mohr-Coulomb公式可以建立起极限状态下抗剪强度和抗拉强度函数。由于坝趾附近压应力很大，在所有荷载的组合下，重力坝可以使坝体保持平衡，多在基岩的接触面和坝底出现重力坝失稳的情况，由于该处单位面积会承受比较大的水平剪力，坝基表面的岩体为破碎岩体，无法和坝底混凝土很好接触，混凝土在出现温度收缩和凝固收缩时，会在接触表面出现一些小的裂缝，在设计过程中，需要对重力坝沿坝基面的抗滑稳定性进行校核。假设坝基面水平的情况下，按照抗剪断公式，极限状态下抗滑稳定函数为

g4=f′∑w+c′A-∑P

式中，黏聚力、摩擦系数、坝基面面积分别为c′,f′和A，总滑动力为∑P，指向下游为正，总垂直力为∑w，垂直向下为正。本文通过使用子域法进行计算，将坝基面作为基岩和坝体的公共边界，划分单元后，可使用如下公式进行标示：

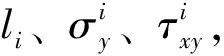
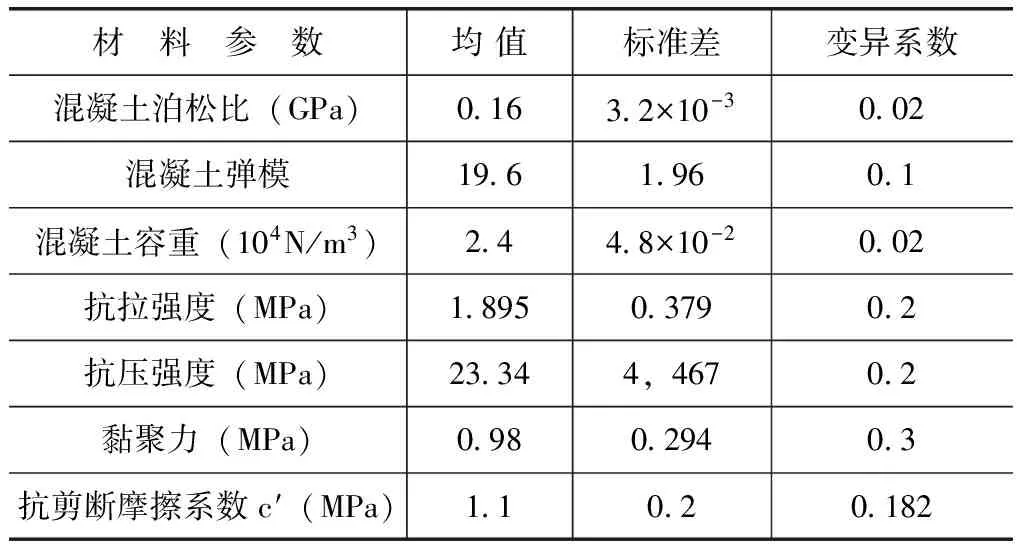
表1 统计后的各个随机变量的特征值

本文将高度为110m的重力混凝土坝作为研究对象，下游坝坡度为1∶0.8，上游坝坡为垂直坝坡，只考虑坝体上游水压荷载和坝体自身重量的作用，边界元划分简图和计算范围如图1所示。

图1 边界元划分简图和计算范围

考虑到混凝土的容重，在大坝修建前，坝基岩石容重会导致基础出现变形，在计算过程中，取计算中的基岩容重为零，库水会导致基础出现位移，而且位移会随计算过程中基础范围出现变化，根据以往计算结果，在计算过程中，把岩基影响范围从坝踵向上游移动到1倍深水中[2]。在使用均匀弹性体对高重力坝应力进行计算时，距离上游坝踵点比较近的位置有一个拉应力区，该区域水的深度是大坝底部宽度的9%～13%，且在坝踵点的周围应力出现了剧烈变化，导致抗拉可靠指标出现了快速变化。当前，在进行重力坝坝踵拉应力计算时，有限元方法还没有得到公认，为了对坝踵抗拉可靠度进行说明，研究具体的变化规律，使用坝基面距离坝踵点3.50m处的拉应力。由于河道坝址位置的天然基岩是由多种因素形成的，不同因素的物理学特征差异比较大，其中岩基变形模量对坝的稳定和应力的可靠度有比较大的影响，在假设基础岩石和坝体混凝土都确定的情况下，使用随机边界元法对重力坝可靠度受基岩的变形特征的影响进行研究。坝趾处抗压强度可靠指标和坝踵附近抗拉强度的可靠指标变化情况如图2所示。

图2 坝趾处抗压强度可靠指标和坝踵附近抗拉强度的可靠指标变化

由图2可知，在岩基弹模不断增加的情况下，岩基会进一步增加对坝体的约束力，导致坝踵四周的应力明显增加，主拉应力也随之增加，这样就会更加容易使坝踵四周出现受拉破坏的情况，因此，在n不断增加的情况下βt会降低。与之对应，在岩基弹模量不断增加的情况下，坝趾位置的主压应力会随着降低，坝趾处更加容易受到压力破坏，使得βc在n不断增加的情况下变大[3]。在弹模比n为1 的时候，βt和βc都可以达到规定的要求，因此，在选择重力坝的坝址时，要使用和坝体混凝土比较接近的弹性模量基岩，坝基弹性模量不可以过高或过低。当基岩变形模量相同的时候，基岩的黏聚力和抗剪断摩擦系数存在一定的差异性，在Ed、Ef不断增加的情况下，c′和f′也会增加，在对坝体沿坝基面的抗滑稳定性进行可靠性指标研究时，如果坝基的岩体都一致，没有容易出现滑动的结构面，坝基面的c′和f′可以根据下页表2进行取值。

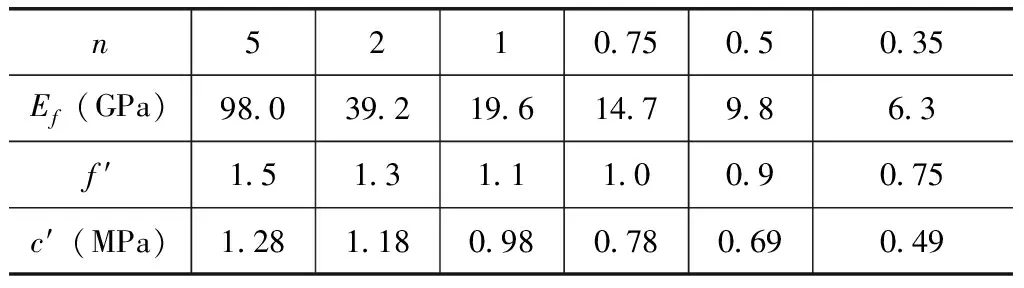
表2 坝基面抗剪断摩擦系数f ′和黏聚力c′

经过计算得出，在基岩变形模量不断增加情况下，坝基面的抗滑稳定性也会增加，因此，在设计重力坝时，要在保证坝踵四周抗拉强度的基础上，选择坝线时，除了要避开容易滑动的结构面外，还需要选择变形模量比较大的基岩，也可以使用基础处理措施提高f′、c′值，进而保证重力坝的可靠性和稳定性[4]。

3 结 语

综上所述，当前我国使用的应力计算方法和可靠度计算方法还处于发展初期，本文只是对边界元法和一次二阶矩法的应用进行了讨论，虽然一次二阶矩法比较实用，但是，使用这种方法会增加随机边界元法工作量，因此，要对一次二阶矩法和随机边界元法的结合问题进行研究，找出与可靠度计算方法相适应的随机数值计算方法，进而寻找出更加适合结构可靠度的应力分析法和计算法。

[1]潘军校,周泽,陈养源.重力坝深层抗滑稳定的可靠度分析[J].水力发电学报,2007(5):93-94.

[2]彭辉,刘德富,田斌.混凝土重力坝安全可靠性时变模型研究[J].水力发电,2009(8):104-105.

[3]张建涛,李俊杰,李留强.重力坝应力的临界能量误差限自适应有限元分析[J].中国科技论文在线,2008(7):117-118.

[4]周伟,常晓林,徐建强.基于分项系数法的重力坝深层抗滑稳定分析[J].岩土力学,2007(2):49-50.

RandomBoundaryElementMethodandItsStudyontheAnalysisandApplicationofHydraulicStructureReliability

JIA Jing-wei

(GuiyangEngineeringInstituteofHydroChinaConsultationGroup,Guiyang550081,China)

Construction structures which have higher requirements for calculation precision, less calculation volume and more complicated structures are usually calculated with boundary element method, thus, this paper studies random boundary element method and its analysis and application on hydraulic structure reliability.

hydraulic structure; random boundary element method; reliability analysis

TV31

A

1673-8241(2014)09-0041-04