波粒二象性理论与波速问题探讨

黄志洵

(中国传媒大学信息工程学院，北京100024)

1 引言

1687年I.Newton[1]的著作《自然哲学之数学原理》出版，标志着经典力学诞生。239年后，即在1926年，E.Schrödinger[2]在量子理论基础上撰写的系列论文发表，在现代意义上创建了波动力学。自那时以来，量子力学著作大量涌现，而且人们不仅关注波动力学的发展[3]，还深入思考波粒二象性(wave-particle duality)，即波动和微观粒子的动力学问题[4]。2008年，笔者的论文“波动力学的发展”[5]发表。它是根据给博士生们讲课的教案经修改整理而成的，论述范围涉及：波动力学的基础；波方程的早期发展；de Broglie波的含意；相对论性波方程；Schrödinger波动力学；用Schrödinger方程分析缓变折射率光纤；波浪理论及水面孤立波；非线性Schrödinger方程(NLS)；逆散射变换法；等。自那时以来已过去了5年，在这期间笔者对波科学问题的研究范围较广；又感到有必要对波科学基础理论及波速问题再作论述，故本文是[5]的姊妹篇。我们特别重视波动的特殊性、波速的本质、波速与粒子速度的关系。为行文方便，我们用CM代表经典力学，QM代表量子力学，WM代表波动力学，QED代表量子电动力学，SR代表狭义相对论，GR代表广义相对论。

2 半经典理论中的粒子轨道与速度[6，7]

正如大家所知，波动光学是用满足线性微分方程组(Maxwell方程组)的电场、磁场矢量来描写电磁波。在几何光学中，光传播被认为是光线沿确定路径(轨道)前进的行为。可以把几何光学看作波动光学的极限情况，即波长趋于零(λ→0)时波动光学转为几何光学。与此类似，在QM中是用满足某种线性偏微分方程的波函数(即微分方程的解)来描述微观粒子和量子波动。在CM中，粒子被看成质点，在由运动方程确定的轨道上运动。通常可把CM看作QM的极限情形，即标志量子化程度的常数(Planck常数)趋于零(ћ→0)时的情况。

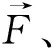
有一个英文词quasi-classic(准经典的)，它有时写作semi- classic(半经典的)。其理论有一个假定是，对这种物理系统而言波函数可取下述形式(de Broglie-Bohm假设)：

ψ=AejS/ћ

(1)

其中S是作用量；之所以作此假定是考虑了波动光学向几何光学过渡时的情况，其时电磁波场分量正是用Aejφ来表达其振幅和相位的。那么对Schrödinger方程而言，当采用上述极限表示的波函数时，代入单粒子在外场中的运动方程(Schrödinger波方程)：

(2)

式中U=U(x，y，z)是势能函数；代入并作微分运算后，按实、虚分开可得以下两个方程：

(3)

对前者取ћ=0，得到

此即单粒子作用量的经典的Hamilton方程。对后者来讲可写作

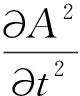
(6)

此即连续性方程，可以看成粒子的几率密度(|Ψ|2=A2)按CM方式的运动状态描写，其速度是经典的粒子速度：

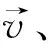
3 关于几率波[8，9]

波函数(wave functon)概念虽然在经典波动中其实也有，但只有在QM中方显得特别突出。先看经典波动中的波函数，例如电磁波中的均匀平面波，电场分量写作：

Ex(z，t)=Re[E0ejφx·e-jkz·ejωt]

=E0cos(ωt-kz+φx)

(8)

这里z是波传播方向，k=2π/λ是波传播单位距离的相位变化，e-kz因子的部分解代表向正z方向传播的波，φx是初始相位。这种波表示法对经典力学也一样，例如对弹性波可以写出

这是时间因子取ejωt的写法。如取e-jωt，写法应为

两种写法在本质上并无不同。这里ψ表示一种扰动随时间、空间的分布状态，例如在弹性波中ψ表示质点离开平衡位置的距离，而在电磁波、光波的情况下ψ表示电场或磁场的某一分量。波动的描写方法与描述质点的力学方法(坐标、动量)是很不相同的。

QM中波函数的复杂化来源于非经典波动的复杂性。这里可以比较光波和与电子运动相伴随的波动。电磁波传播时展布于空间的波动是有能量、动量的客体，具有物质性特征。与此相对照，电子的物质波仅为几率波(probability waves)。波函数最早由Schrödinger方程提出，但他过份强调波动性，认为一切物理现象均可归纳为波，力学过程可归结为波群的运动，波函数是描写物质波振幅的函数。那么究竟什么是粒子?在他看来粒子不过是集中起来的波群，或者说粒子不过是Schrödinger方程(SE)的本征解叠加而成的波包(wave packet)。N.Bohr对此作了批评，指出波包在传播过程中不断“发胖”导致了不稳定性，而粒子实际上却是稳定的。因此，Schrödinger虽然提出了著名的QM波方程而作出了划时代的贡献，但存在不足，未能正确解释波函数的本质。针对这种情况，后来有人开玩笑说：“Schrödinger方程比Schrödinger更聪明。”

这是波函数归一化条件。

根据电子双缝实验可以总结以下两条：①对处在同一状态下的大量粒子(电子)而言，波函数模的平方|Ψ(x·y·z，t)|2与t时刻在空间(x，y，z)处单位体积内的粒子数成正比；亦即在波强度大的地方粒子数必定也大。②对单个粒子(电子)而言，波函数模的平方|Ψ(x·y·z，t)|2与t时刻在空间(x，y，z)处单位体积内发现粒子的几率(即几率密度)ρ(x，y，z)成正比。因此，无论对处于相同条件下的大量粒子的一次性行为，或者单个粒子的多次重复性行为，Born的波函数统计解释都有效。上述情况的第②是特别令人感兴趣的；电子通过双缝的干涉代表单个电子的波的干涉，即一个电子自身的干涉，电子的干涉条纹是许多处于相同状态下电子体系的多次积累效应。

因此，不能认为必须由一群粒子组成波，因为实验已表明那怕只有一个电子也具有波动性。虽然我们不能根据波函数预言粒子在某时刻一定会在某处出现，但却可知道粒子在该时该处出现的几率有多大。由此可得出两点结论，首先，微观粒子的波动性在很大程度上是由统计性规律决定的；其次，波函数所代表的是一种几率波。因此，在QM中讨论的波与过去人们熟悉的经典波有很大的不同。

4 真空中光速的性质和波速的标量性

为什么光(确切说法是光波)在真空中的行进速度c等于光(光波)在真空中的波长与光(光波)频率f的乘积？认识到这一事实是由于20世纪初期人类在理论认识上的进展。正如N.Bohr所说，Einstein对早期量子理论的突出贡献在于认识到光电效应之类的物理现象是取决于个体的量子效应。或者说，任何频率f(波长λ)的辐射均有粒子性，而粒子的能量E及动量p为

E=hf

(9)

p=h/λ

(10)

式中h是Planck常数；现在讨论在真空中运动的光子(质量m)，其动量p、能量E为

p=mc

(11)

E=mc2

(12)

联立以上4个方程，可作如下运算：

故得

c=λf

(13)

这个推导过程清楚地表明，c既是光子的运动速度，又是光波的传播速度。笔者在2013年6月发表了一篇文章[12]中的结尾处的若干说法是错了，当时自己评论说：“国际计量组织所定义的真空中光速c，暗含一个前提‘光是波动’，因而c仅由是标量的f、λ决定”。以上推导则表明，由真空中光波长λ和真空中光的频率f这两个量(它们均可极为精确地测定)相乘而得到的c，虽从表面上看是由波动参数得到的，但它无疑也是作为粒子的光子在真空中飞行时所具有的速度。……因此，[12]的一些后续说法也错了，我们已作改正。

真空中光速c是一个由两个标量所确定的标量，这是事实。如回顾国际计量界在上世纪后期精测作为基本物理常数之一的c值的情况，对此会有更深刻的认识。1958年以前，已有的测c方法的精确度不能令人满意。英国物理研究所(NPL)的科学家K.D.Froome发明了被称为“自由空间微波干涉仪”的技术，把光速测量提高到误差小于±100m/s；1958年他在72GHz频率上得到的值c=(299792.5±0.1)km/s。到这时，测量精度已达3.3×10-7，此后科学界曾长期使用Froome的数据。微波方法的缺点是：波长大，测量准确度受到限制，衍射带来较大误差。1960年发明了激光，它为精密测量c值带来了全新的可能性。到1969年，国际上已测出氦氖激光器的波长为：λ=3.392 231 376μm (按氪谱线重心线定义)，或λ=3.392 231 404μm (按氪谱线最大光强点定义)。这意味着波长测量精确度已达到3.5×10-9的水平。把激光波长乘每秒产生的波的数目，就得到每秒内激光走过的距离(光速c)。可见，需要精测激光频率；具体说，需要完成一个光频测量链，技术要求高，由一个国家的最高计量机构来研究是最恰当的。1972年美国标准局(NBS)K.M.Evenson等[13]采用高度复杂的技术对甲烷(CH4)稳定激光完成了测频；实验中采用了铯(Cs)原子频标出发的激光频率链，其中包括6台不同的激光器和5个微波速调管；结果得到

fCH4=88.376181627×1012Hz

(14)

测量精度达6×10-10；故可算出真空中光速

c=λCH4fCH4=299792456.2m/s

(15)

误差仅1.1m/s，即精度3.6×10-9。这样一来，光速c的测量精度比微波方法提高了100倍。人类终于能把光速测得这么精确，确实是巨大的进步。

在实现了光频测量之后，如何确定c的标准值(也叫国际推荐值)，曾经历了一个过程。最后定下来的值并不是K.M.Evenson于1972年报告的值。我们知道，计量学中的长度基准(米定义)自1960年以来是采用Kr-86的605.7nm谱线作为基准，但该谱线存在轮廓不对称性，造成其重心点与光强最大点之间有1×10-8的波长差异。这一情况在研究光速c的问题时成为有价值的参考。甲烷(CH4)谱线的波长值约为3.39μm，1972～1973年间国际上的著名计量学机构曾得出下述的精确测量值：

λCH4=3.392231376(12)μm 美国标准局(NBS)

3.392231376(8)μm 国际计量局(IBS)

3.39223140(2)μm 加拿大国家研究委员会(CNRC)

前两个是按重心点定义，后一个是按中间点定义。国际米定义咨询委员会(CCDM)于1973年6月决定，采用以下数据作为甲烷谱线波长的标准值(推荐值)：

λCH4=3.392 231 40 μm

(16)

不确定度为4×10-9。和前述的NBS的fCH4测定值相结合，可得c=299792458.33m/s。故CCDM于1973年将c的标准值确定为

c=(299792458±1.2)m/s

(17)

不确定度为4×10-9。后来(1972～1974年)虽然又出现了几个新的测量值，但均在上述标准值的不确定度范围内。因而，1973年国际天文联合会、1975年国际计量大会都认可了这个值。这样，现在有了c的真实值(真值)，其误差在±1.2m/s以内。

精测真空中光速c的成功有重要意义。正如大家所知，基本的计量单位有7个，即米、千克(公斤)、秒、安[培]、开[尔文]、摩[尔]、坎[德拉]。在这些基本物理单位中，精度最高的是时间(频率)；2014年1月有报道说，美国国家标准与技术研究院(NIST)新制成的锶晶格钟(原子钟的一种)获得了破记录的精准度，50亿年不差1秒，水平之高令人吃惊。我们知道在1957年制成铯(Cs133)原子钟；1967年国际上规定的秒定义为，“Cs-133原子基态的两个超精细能级之间跃迁所对应辐射的9192631770个周期的持续时间”；自此确立了与天文时间不同的原子时间。但铯钟的精准度为1×10-13，即30万年不差1秒。40多年后的今天，原子钟的水平提高了4个数量级，达到1×10-17。

其次要考虑的基本计量单位是长度，正是它与c值有联系。米定义方法早期用原器，1960年才开始按原子的辐射跃迁来定义，即“Kr-86原子的2p10和5ds能级之间跃迁所对应的辐射在真空中波长的1650763.73倍”；相应的长度基准称为Kr-86基准。尽管按原子状态来定义比起过去优越，但仍存在的问题：对同一辐射(同一跃迁)，波长是一种单位，频率又是一种单位，二者互相独立，建立计量基准的方法也不同；这就不合理，能否统一起来，从而减少一个基本单位? 当时认为由于精测真空中光速c达到了高水平，出现了用下式定义长度的可能：

式中c是恒量，频率f是基本单位，波长λ成为导出单位。这样，长度不再是基本单位，而是导出单位，解决了前述第1个问题。1983年，国际上规定了新的米定义：lm是平面电磁波在真空中在(299792458)-1s内走过的距离(规定平面波是为了避免曲率半径修正)。由于国际上对光速c的测量取得了重大突破，c成为指定值(299792458m/s)，计量学跃上了一个台阶。……当时这种作法是以光速c的绝对不变性、恒定性、稳定性为基础的，现在来看还须作进一步研究。而且，在实际中出现(应用)的电磁波与平面波相去甚远；从这些方面看，这个米定义是存在问题的！正如计量学家沈乃澂指出的，现在需要研究光速恒定性的适用范围及可能的微小变化，这对物理学、计量学进一步修改单位的定义非常重要。

为测定光速的值，人类探索了很久，最后才找到这个方法——计量同一光波(电磁波)的频率f和真空中波长λ，再用c=λf得出真空中光速的精确值。这是已知方法中最好的方法，其实现有3个要点：首先是激光的发明(激光不是自然界天然存在的)，提供了供实验用的单色性极好的光；其次是标量方程c=λf，这个方程来源于人类对自然界的基本而重要的认识，而且好的光源保证方程的有效性和精确可实现性；最后是科学家们的高度智慧，使整个测量具备了可操作性。……实验的成功又使人们认识到电磁波波速的“标量性”(characterity of scalar)，并把WM和CM区别开来。研究波科学确实不能完全沿用过去的经典性、习惯性思维。而近年来众多的负群速(NGV)实验的成功，进一步证明把测到的负波速(vp<0或vg<0)仅看作“运动方向反了过来”是不妥的。当然，有的科学名著(例如Born和Wolf[14]的书)也对“波速是标量”作了理论上的推导和证明。……总之，对电磁波(包括光)而言频率f、波长λ、幅度A、相位Ф、相速vp、群速vg都是经典的标量，认识这一点很重要。

在Born和Wolf的论述中，把波方程的实解写为更一般的形式：

式中A(>0)和g是位置的标量函数，而g(r)=常数是等相面(波面)；相速定义为

两位作者明确指出，相速不能作为一个矢量。另一方面，群速被定义为

式中ω0是中心频率；对平面波而言，就有

群速同样不是矢量。过去有一些电磁理论、微波理论的著作[15-17]，都回避讨论波速是矢量还是标量的问题。Born和Wolf的书(近年来一直由Wolf主持修订和再版)并不回避。而且在第7版中还根据2000年《Nature》发表的WKD实验[18]，补充了以下的话语：“在反常色散区域，群速可超过真空中光速或变为负；但这与SR并不冲突”。

5 物质波波速和de Broglie科学思想演变[3，19]

法国物理学家L.de Broglie(1892—1987)的早期工作是WM的起点。20世纪初科学界的研究重点是电子和原子，其间有3件大事为：Planck量子假设(1900年)、Einstein光子学说(1905年)、Bohr定态跃迁原子模型理论(1913年)的提出。光子学说问世后，人们已开始关注波动和粒子的关系；然而如果研究一个电子束流，也会看到波动现象。电子具有波粒二象性，能产生衍射现象。问题在于波长是多少？这可由衍射环的间距而作判断；测量显示波长λ取决于电子的速度，而速度由对电子加速的电压决定。总之，结果表明λ与速度v成反比(λ∝1/v)，电子越快波长越短。这个实验关系有一个常数存在，而它恰为Planck常数与电子质量之比(h/m)，故得

上式中分母为电子的动量(p=mv)，故有

上述关系式是在1924年由de Broglie发现和证明的。现在可以看出，v和p是对粒子的描写，λ是对相应的波的描写，而Planck常数(h)把二者联系起来。而Einstein此前的发现是类似的，正是h把光波频率f与光量子能量E联系起来(E=hf)。

1923年de Broglie为了解释Bohr原子理论与实验的矛盾，参考了光子学说形成的“波—粒二元体系”思想，在其博士论文(1924年发表)中提出了物质波(matter waves)的概念，为后来Schrödinger创建WM作了准备。物质波思想认为凡微观粒子(不限于光子)均由波伴随，其频率为

式中E.为粒子能量；而物质波波长为λ=h/p；后一关系式被1927年的电子衍射实验所证明，故1929年的Nobel物理学奖授予de Broglie。此后的发展表明，de Broglie波长对于认识一个物理体系具有重要意义，当物理系统的特征长度与该波长可比拟时，物质波就很重要(原子中的电子即为一例)。

一个波的参量不仅有波长λ，还有频率f、波速vp，它们之间的关系为

λf=vp

(26)

在光波情况下，vp=c。对电子波而言，需要掌握的参数是f或vp；但不幸的是无法由实验确定电子波的f和vp，故需从理论上作进一步考虑。现在我们面对的是粒子速度v和波速度vp，可否假设v=vp？回答是不行，因为已知λ强烈地取决于v，因而这会使λ强烈地取决于vp——借用光学中的语言，这是强色散。我们知道在光学中(或说在电磁波理论中)波速度有相速(vp)、群速(vg)之分，见公式(20)和(22)，由于k=2π/λ；故可得

除非vp与λ无关，否则vg与vp是不一样的。我们都知道对描写电磁脉冲(波脉冲)而言必须用vg；它也称为波包，并无单一的确定波长。一个波包含有相速不同的多个频率成分，中心频率f0(对应波长λ0)；可以认为波包的速度是vg(λ0)，它不同于vp(λ0)。当然，对光脉冲而言，色散小时两者可认为是近似地相同的。

在电子波情况，一个粒子类似于一个小波包，可以取

v=vg

(28)

即粒子速度等于群速；这一假设有实验事实证明[3]。因此可写出

把λ=h/mv(de Broglie波长关系式)代入，可以导出

故有

也就是

等式右方为粒子动能E，它对应频率f的电子波能量：

E=hf

(30a)

在电子波情况下，v=vg关系式可由另一途径而证明；首先推出：

vp=λf=(h/mv)·(mc2/h)=c2/v

(31)

以上推导引用了质能关系式；根据SR，v≤c，故有vp>c，即在遵循SR理论时物质波的相速大于光速。de Broglie认为相速不传递信息，完成此功能的是群速vg，并证明

vgvp=c2

(32)

故粒子速度即群速(v=vg)；必须注意，只有承认相对论正确(粒子不可能运动得比光速快)，才有de Broglie波速(相速)比光速快的结论；而群速仍然是亚光速。

既然de Broglie波的相速不是信息的速度，也不是粒子的运动速度，过去几乎无人重视de Broglie波的超光速，不认为是一个问题。但在这里，我们却看到物质波与电磁波(光波)的重大区别，对后者而言在自由空间(真空)中传播的速度就是vp=c；如果vp>c，便称为“异常传播”，需要特殊的理解和解释。故电磁波与物质波之间存在奇怪的不对等。

总之，物质波(实物粒子波)与机械波(水波、声波)和电磁波(光波)很不一样。机械波的发生是由于介质中质点的振动，电磁波是电场、磁场的振动在空间的传播。物质波却没有这种直接的物理意义。由于其强度代表粒子出现几率的大小，故物质波本质上是几率波。

在物质波现存理论中还有一个关系式：

这也是不好理解的——vg与vp怎么会有确定的数值关系?! 但正如W.Heitler[3]所说，这个关系式不具有重要性。实际上，电子波的vp缺少真正的物理意义，也不是可测的物理量(电子波频率f也不是可测量)。电子波相速只有纯数学的意义。……诸如此类情况都和电磁波(光波)不一样！

为了深化对波科学的认识，回顾和思考de Broglie科学思想的演变是必要的。1927年10月在比利时Bruxell召开了第5届Solvy会议，以“电子和光子”作为中心议题。在W.Bragg和A.Compton作学术报告之后，de Broglie最先发言。他回顾Schrödinger波方程和M.Born对函数ψ的几率性粒子诠释方面的工作，表示在波动力学和粒子力学方面确已取得了进展。然后，de Broglie问道：“能量呈点状集中的理论，以及假定有ψ波存在的理论，都很成功；但二者如何协调一致?粒子和波的联系是什么?”随后，他提出了自己的波导引理论(la théorie de Lónde-pilote)，它强调的是粒子而不是波。1927年的de Broglie双重解理论还不是非线性的；它是说QM波方程有两个解：其一是连续波函数ψ，是单色平面波；其二是奇异解，奇点代表粒子。并且，前者为后者导向(导航)，而粒子仿佛是跨在波上。波导引理论在会议上未受支持(以后de Broglie自己也认为有问题)。20世纪50年代以后，de Broglie重视和强调的是一个非线性方程的双重解理论。

1940年，de Broglie认为现有QM形式体系不可能与GR相协调。1953年，Einstein在致de Broglie的信中说：“你建议以下式表示物理实在的完整描述，即

ψ=ψΩ

(34)

式中余因子ψ代表波结构，Ω代表粒子结构。无疑这里包含着能在实验上接受的令人满意的双重结构概念。”……在后来的双重解理论中，de Broglie以下式代替前式，即

ψ=Aexp(jS/ћ)

(1a)

式中A为粒子结构，而指数项表示波。故相速在指数项中大于光速，而群速在A中小于光速。

总之，de Broglie认为物质波应被描述于物理空间而非组态空间，而粒子必须永久局域在物质波中。自20世纪50年代起，他开始重视非线性的作用，认为要正确描写波和粒子的缔合必须有两个方程：一个是描写波动的线性方程；另一个是描写粒子结构的非线性方程。从20世纪50年代初de Broglie开始关注非线性方程，并引用19世纪发现的孤立波(solitary waves)的例子。1956年de Broglie指出，与物质波相缔合的粒子形状与孤立波十分相似，方程中的非线性项将使表征粒子的奇异解成为可能。de Broglie和他的学生们所说的“驼峰波”、“驼峰解”实际上就是孤立波和孤立子(solitons)，并体现了de Broglie的下述思想：粒子就是局域于波中的峰。

联系到后来对非线性Schrödinger方程(NLS)的研究，1971年Zaharov和Shabat用逆散射变换法求解NLS，得到亮孤子解，后来用于描述反常色散时窄脉冲在单模光纤中的传播。孤子的特点是恒速运动和相互作用后不变形，呈现出鲜明的粒子性质。问题是，NLS方程的单孤子解是单个粒子还是系综?为分析起见，必须回忆de Broglie的一个论点：“只有群速才等于粒子的运动速度”。现在，孤立波所在的有效区间称为“奇异区”。de Broglie曾证明，如奇异区的运动速度代表粒子速度，则它必为小于光速的群速。但Schrödinger方程(包括NLS)中的速度▽S/m只是相速。而且，由于Schrödinger方程没有相速、群速之分，故该奇异区不可能是单个质点(de Broglie说粒子速度只能是群速)。因而，NLS方程的单孤立子解可能不是单粒子而是系综。

总之，de Broglie对波动力学的创立和波粒二象性的研究做出了很大贡献，对他的工作仍有许多深入讨论的余地。例如，de Broglie的物理思想与Bohr不同；Bohr相信一种两面性的物理实在，即某种情况下表现为粒子的东西在另一种情况下表现为波。而de Broglie则认为，只有一种东西——波和粒子的缔合，在同一时刻既是波、又是粒子。再如，如何从物质波出发研究超光速性(superluminality)。……笔者同意物理学家艾小白的意见——对de Broglie波的研究仍是待开垦的处女地。

6 关于光波和光子的本质

前已述及，对光的研究的一项成果是认识到光波速度和光子速度的一致性。但长期以来对光波和光子的本质仍然缺乏清晰的认识，对光的波粒二象性仍在激烈地争论[20-22]。查阅物理学史书籍可知，1672年I.Newton叙述了他所做的实验，用三角形玻璃棱镜把日光分开为不同折射角的光就得到了7色光谱。在同一时期Newton又用光的微粒性假说解释光在界面上的反射。1690年C.Huygens提出“光是一种波动”的理论，其中包含了“子波”、“波前”等概念。1802年T.Young做了光的双缝干涉实验，对“光是波动”提供了实验证明。1818年A.J.Fresnel计算了狭缝、圆孔、圆板等障碍物造成的衍射花样，与实验相符；Fresnel被认为发展了Huygens原理。至此，多数物理学家相信光的波动说。1865年J.C.Maxwell提出光是一种“按电磁规律通过场传播的电磁扰动”，即电磁波；1887年H.Hertz以实验发现了电磁波。光的波动说的发展暂告一个段落，整个过程经历了大约200年。据此人们建立了电磁波谱图，在这个图上可见光(visiable light)只是中间的一个与人眼能力相适应的狭窄区段。

在1905年QM尚未问世，Einstein的光量子假说是从经典物理学出发而论述的。Einstein认为，用连续空间函数来运算的光的波动理论，在描述纯粹的光学现象时，已被证明是十分卓越的，似乎很难用任何别的理论来替换。可是光学观测都同时间平均值有关，而不是同瞬时值有关。尽管衍射、反射、折射、色散等等理论完全为实验所证实，但仍可以设想，当人们把用连续空间函数进行运算的光的理论应用到光的产生和转化的现象上去时，这个理论会导致和经验相矛盾。因此Einstein假设，从点光源发射出来的光束的能量在传播中不是连续分布在越来越大的空间之中，而是由有限个数的、局限在空间各点的能量子所组成，这些能量子能够运动，但不能再分割，而只能整个地被吸收或产生出来。

Einstein的光子假说成功地解释了用经典电磁理论无法说明的光电效应。1905年—1914年，R.Millikan以长期实验证实了Einstein光电方程的正确性。1921年和1923年，Einstein和Millikan分别获Nobel物理奖。1924年，A.H.Compton测到了X射线被石墨散射时波长变长的现象。在解释时考虑了光子的动量，当光子碰撞电子时是可以计算X光被散射时产生次级X光波长的变化，计算与实测一致。至此，光子假说得到进一步的证明，Compton获1927年Nobel物理奖。因此我们看到，到1924年为止“光是波动”一说并未被谁否定掉，与此同时又确立了“光由许多光子组成”。这样，就出现了后来的复杂情况。

2004年，M.Chown在《New Scientist》杂志上发表了一篇文章，其中说：

“迄今没有多少人知道Einstein对巴西的访问。那次旅行是1925年3月5日从汉堡(Hamburg)出发的，做3个月的南美之行。……当时，巴西科学家们齐聚在里约热内卢(Rio Janeiro)，期待着听Einstein讲相对论。但他本人却另有想法；对Einstein而言，相对论只是19世纪经典物理学的扩展，而在他一生中的革命性成果却是光子概念，这才是他要讲的东西。但波伸展在整个空间，而粒子却是分立的实体，如何统一这两者?Einstein并未找到答案。

纽约城市大学(City Univ.of New York)的R.Campos现在把档案馆中的文稿译成了英文。在文稿中，Einstein不能解释光子为何可以既是波又是粒子，无法得出能说明两方面矛盾性质的数学图景。当然，由于Einstein使用经典物理学，这是不可能做到的……。在Einstein的巴西讲学的一个月后，德国的W.Heisenberg发明了一种新的物理学，即量子理论。Einstein看不到(不能看到又不想看到)的要点是，光子不是一个经典的东西。1925年5月7日在巴西科学院作报告的那个夜晚，标志着Einstein作为前沿科学家生涯的终结。直到去世，Einstein都不接受Heisenberg的量子理论，该理论用不确定性取代确定性。Einstein在里约热内卢的讲话，表示他仍绝望地希冀他于1905年放出的‘妖怪’(光子)仍可用老的经典物理去驯服。”

|nk〉=ћ

(35)

光子数算符(k模式)为

(36)

以上各式中|nk〉代表nk个光子的状态，而其光场平均值为零。

用谐振子量子化方法可得出相同的结论。总起来讲，量子化之后的电磁场是用光子数算符的本征态|nk〉来描述的，它代表含有nk个k模光子的态。因此，现在我们统一地用较简单的下式表示，即对单模电磁场有

=ћ

(36)

由此可知，k模电磁场的能量不是nћω，而多出一项。当空间不存在光子时(n=0)，模的能量不为零，而是ћω/2。这叫零点能(zero point energy)，它的发现正是电磁场量子化理论本身的成就。现在，真空在量子理论中看作基态，记为|0〉。可求出基态能量为

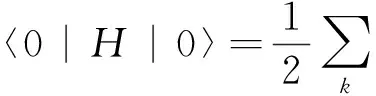
(37)

实际上是说零点能量为

上述分析用电磁场的量子化方法对波粒二象性提供了基本的数学解释，即连续性的电磁场(以及电磁波)在量子化之后得到的结果是光子，因而场(以及波)被看成粒子数目极大的系统。但仍不能给出具体形象化描述。回答不了“光子是什么”的问题。

1951年Einstein[24]曾企图仍从Maxwell方程组探求光量子的物理起源和本质，但未见成效。正是在这一年他说：“经50年思考还不能回答光量子是什么”[25]。自那时至今又过去了63年，那么我们现在是否清楚地了解光子是什么?人们仍在就“波粒二象性”展开争论，说明问题仍未解决。实际上，关于光子的粒子性质是一个难办的课题。人们都承认，把光子当作点粒子是不正确的。另一方面，遵循SR的观点，光子没有静质量(m0=0)，故CM难于在这种“无质量粒子”的身上应用。使用相对论力学也是困难重重，因为对光子而言，

m成为任意大小，是不可接受的；如取m0≠0，m=∞，这也不可接受。相对论力学处理光子这种客体显得力不从心。

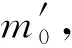
上式等号左端是入射情况，fi是入射光子频率；等号右端是碰撞后情况，v′是反冲电子速度，f是被电子散射后的光子频率；再引入动量守恒，联立这些方程可得

由于Compton效应，许多人把电子、光子都想象为圆形球体，但这是荒谬的！尽管Compton实验证明了光子和电子一样都是物质实体，具有正实数的动质量，又证明了在微观粒子的单个碰撞事件中动量守恒、能量守恒；但光子却不是一个弹子球，不能主要依靠经典物理学去处理。例如我们如果企盼“测出光子直径”，恐怕永远都不会有结果。按照自己熟悉的宏观概念去看待光子是徒劳的。

如果使用波粒二象性的描述方式，那么在这方面电子的情况比光子要好。光的波粒二象性，其中的“波”是什么波？虽然电子的波动是几率波，但光子的波动一方面是经典性的电磁波，但又似乎可能是几率波。然而经典电磁波并不是几率波，这就发生了矛盾。电子几率波对应Schrödinger方程，有一种观点认为“光子几率波”(假如成立)却没有可对应的波方程。可否对光子摒弃几率波概念?可是在双光子纠缠分析中还用得到这一概念。……诸如此类的矛盾和问题仍在困扰着物理学家[22]，期望今后有更好的理论和实验来说明有关的物理现象。

英国刊物《New Scientist》曾在2004年、2007年连续报道一个关于波粒二象性的实验[26，27]，研究者是在美国工作的伊朗科学家Afshar。文章说，Afshar的实验和理论大大动摇了量子论，在物理学界引起了很大的震动。实验挑战了由Bohr在80年前提出的一个原理。它和亚原子例如电子和光子有关，这些亚原子似乎在某些实验中具有粒子的特性而在另外一些实验中又具有波的特性。根据Bohr的说法，这些粒子特性和波动特性是互补的，没有一个实验可以同时显示这两个特性。在Afshar得出结论之前，似乎没有任何实验和这个原理相矛盾。他实验的设置是以双缝实验为基础，但在小孔屏幕的远端有一个透镜。透镜重新将分散的光束聚焦到两个镜子上，镜子会将光束分别反射到两个粒子探测器上，这可以让Afshar找到光子的路径。根据Bohr的互补性原理，那意味着没有干涉图像存在的证据，Afshar观察到的是光的粒子性，而不是波动性。通过在干涉条纹暗条纹的地方将金属丝放置在透镜前方的方式间接地观察到了干涉现象。Afshar争论说，如果光子没有干涉，那么将没有暗条纹并且金属丝将挡住一些击中透镜的光子，减少探测器捕捉到的粒子数量。但是信号中看不到这样的迹象，这暗示着光确实形成了干涉，这和互补性原理不符。后来，Afshar改进了他的实验以便可以测量光子的路径，同时可以观察它们的波动，比如干涉图像。修订的实验发表在期刊Foundations of Physics (37卷，295页)，这本期刊现在的主编是Nobel奖获得者物理学家G.Hooft，他也相信“量子论有着基础性问题”(New Scientists，2006年5月6日，8页)。……

我们认为，上述情况说明波粒二象性研究离彻底解决问题还很远，有关探索都值得鼓励。但说量子理论已被动摇(或颠复)，则为无稽之谈！我们知道，在Bohr看来，对一个微观粒子而言，既然同时测量位置和动量是互相排斥的，人们只能在互补的意义上去获取对客体的认识。亦即在QM中位置和动量是一对互补的可观察量。实际上对“互补性”可作如下表述——对每个动力学自由度存在一对互补的可观察量。笔者认为，当人们谈论“波粒二象性”的时候也就是在谈论“互补性”。这在本质上既是从QM出发所作的阐述，又是对QM的捍卫。今天我们如果承认QM 80年来的成就辉煌，就不会认为Bohr错了(至少是无大错)。至于Afshar说“我怀疑光子的存在很长时间了”，这更是荒唐！作为物理学家，应当知道单光子(single photon)的产生和应用技术已有很大发展[28-34]；而且光子学说的基本理论前提也是正确的。

7 讨论

负责分析处理微观粒子的力学，无论称之为QM或WM都可以，它在诞生后取得了巨大的成就。这门学科基础扎实、精采纷呈；例如虽然Schrödinger方程可以看成一个理论假设，但它的正确性、预见性是由于与实验一致而确立的；并且在实际上Schrödinger先创立了不含时方程，后来才创立含时方程。而在λ→0的极限时，预期含时Schrödinger方程(它是WM的基础)将还原为Newton第2定律(CM的基础)。不仅如此，质量为m的粒子在势能U的区域运动时，波函数Ψ所服从的波方程即Schrödinger方程，粒子性和波动性巧妙地通过一个方程式联系了起来。波函数Ψ的内涵丰富，而QM在本质上是统计性的。所有这一切优美地结合地一起，卓越地证明着人类智慧对自然的深刻理解。

Heisenberg[35]的不确定性原理(uncertainty principle)也是如此；它不是空想的产物，而是来源于对电子束通过狭缝时的实验表现的分析。正是波粒二象性限制了同时测定粒子的位置和动量的能力——位置测量越是精确，动量测量的误差就越大。笔者曾论述过量子波动[36]，简单地证明它与测不准关系式之间有内在的一致性。实际上，波粒二象性与测不准关系也是互相印证地一致。

回到波速问题；说“速度是一个宏观概念”无疑是正确的。在QM中速度表示什么？其实无法回答。然而在实际上仍然需要和使用速度概念——真空中光速c就是速度，难道QM对c采取排斥态度不予承认？不确定性原理也是QM的一个组成部分，对其物理意义的讨论就离不开速度。经典理论并非一无可取，我们必须正确看待经典物理与量子物理的关系；前者有局限性并不表示它已被彻底推翻。又如我们都知道对光子的解释需要使用QM和QED，但人们可以继续使用Maxwell方程组来研究光子在空间的传播，就是一个很好的例子。对CM中的速度概念也应作如是观，否则就会陷入迷茫。众多事实已经表明，波速概念的运用不仅充实和丰富了WM，而且推动了波科学的发展。……我们曾在[36]中讨论研究负波速(NWV)的意义和进展情况，有关实验虽然有一些是经典物理性质的，但也有另外一些却是真正的量子光学(Q0)实验。尽管对NWV的解释各种各样，但仍在使用速度这个参量却是事实。

对波粒二象性，许多人会说这是老课题，早已解决没有再研究的价值。但也有众多物理学家认为它仍是现代物理学最大谜团之一！我们认为从理论和实验再作探讨是有益的，但不应过分追求具体化、形象化的结果。这是因为在量子世界中，粒子和波之间的关系紧密，二者的区别变得非常模糊；人们习惯的“大、小”、“快、慢”之类的概念也变得含糊不清缺乏意义。因此对问题的追讨恐怕也有个限度。况且不能忘记，迄今为止尚不存在能解释一切物质和物理现象的完善的理论。

8 中国学者的若干意见和贡献

至于笔者对电磁波的研究，是从1963年开始的；其时黄宏嘉先生的《微波原理》刚出版[17]，我们立即仔细研读了该书。同年笔者在《电子学报》发表论文[41]，对利用消失场(evanescent fields)状态的截止波导衰减器作理论分析和实验研究，这是我们对波科学研究的开始。几十年来研究工作大致沿着以下方向：①对各种形式的导波系统作深入分析和探索，重点放在两种最常见的器件(圆波导、矩形波导)上；但它们是使用电介质和金属的混合系统[42-44]，普遍的理论应当能够处理，而在近似条件满足时就成为纯金属系统的理论；②通过对波导普遍化的特征方程(即本征值方程)的推导了解和掌握全频域的物理特性[45]，但在有截止频率的情况下对低于截频(f

在我们的语境中，2000年曾把多国所报道的超光速实验称为“电磁波异常传播”(anomalous propagation of EM waves)[74]；但在2001年又把波的负折射研究称为“微波异常传播”(anomalous propagation of microwaves)[72]。这是早期情况，后来一般不这样说，因“异常传播”的含意不甚清晰。……总的讲，由于50年来笔者对电磁波的多角度的探索，波科学的内涵逐步展示，其规律逐步被掌握。涉及范围也不限于导波系统(如TEM传输线、波导、光纤等)，而深入到一些不为人注意的地方——例如天线的近区(near region)。……虽然多数研究工作的开拓(正如黄宏嘉先生所说)是依靠经典电磁理论而完成的；但我们极为重视对量子理论的学习和应用[66，67，75]。而且一直密切关注学术界的动向，例如，范洪义教授的著作《从量子力学到量子光学》[76]一书的出版，就是中国学者的出色贡献，值得推荐！

9 结束语

2003年，量子光学专家A.Zajonc[77]说“光量子不可捉摸……我们对它的无知与Einstein当年差不多”；这是指1951年Einstein的言论(“经50年思考仍不知光子是什么”)[25]。因此有人说至今“光的本性问题尚未解决”[22]也就不奇怪了。此说如成立，对电磁波会有同样的判断，即研究工作尚在起始而非终结。至于物质波、几率波，也都还需要再作探索。“波粒二象性”的谜团也仍未破解。

科学家的本性就是总在发现问题而非计数成绩；“生有涯而知无涯”。自然的深奥和神秘就这样引导着人们不断地向前！

[1]Newton I.Philosophiae naturalis principia mathematica[M].London：Roy Soc，1687.(中译：牛顿.自然哲学之数学原理[M].王克迪，译.西安：陕西人民出版社，2001.)

[2]Schrödinger E.Quantisation as a problem of proper values[J].Ann d Phys，1926，79(4)：1-9.(又见：Schrödinger E.Lectures of Schrödinger.中译本：范岱年、胡新和，译，薛定谔讲演录[M].北京：北京大学出版社，2007.)

[3]Heitler W.Elemantary wave mechanics[M].Oxford：Clarendon Press，1956.

[4]黄志洵.波粒二象性理论的成就及存留问题[J].北京广播学院学报(自然科学版)，2000，(4)：1-16.(又见：黄志洵.波粒二象性理论的若干问题[J].中国工程科学，2002，4(2)：54-63.)

[5]黄志洵.波动力学的发展[J].中国传媒大学学报(自然科学版)，2008，15(4)：1-16.

[6]Bohm D.Quantum Theory[M].London：Constable and Co，1954.

[7]Landau L，Lifshitz E.量子力学 (非相对论理论)[M].严肃，译.北京：高等教育出版社，2008.

[8]周公度，段连运.结构化学基础[M].北京：北京大学出版社，1997.

[9]倪光炯，陈苏卿.高等量子力学[M].上海：复旦大学出版社，2004.

[10]Maxwell J C.A dynamic theory of electromagnetic theory[J].Phil Trans，1865，(155)：459-512.

[11]鲁绍曾，等.现代计量学概论[M].北京：中国计量出版社，1987.

[12]黄志洵.“光障”挡不住人类前进的脚步——纪念第242次香山科学会议召开10周年[J].中国传媒大学学报(自然科学版)，2013，20(3)：1-16.

[13]Evenson K M，et al.Accurate frequency of molecular transitions used in laser stabilization：the 3.39μm transition in CH4and the 9.33 and 10.18μm transition in CO2[J].Appl Phys Lett，1973，22：192-198.

[14]Born M，Wolf E.Principles of optics(7th.Ed)[M].Cambridge：Cambridge University Press，2003.

[15]Stratton J A.Electromagnetic theory[M].New York：McGraw Hill，1941.

[16]Brillouin L.Wave propagation and group velocity[M].New York：Academic Press，1960.

[17]黄宏嘉.微波原理(I)[M].北京：科学出版社，1963.

[18]Wang L J，Kuzmich A，Dogariu A.Gain-assisted superluminal light propagation[J].Nature，2000，406：277-279.

[19]de Broglie L.Nonlinear wave mechanics[M].New York：Elsevier Publ.，1960.

[20]黄志洵.光是什么[J].中国传媒大学学报(自然科学版)，2009，16(2)：1-11.

[21]黄志洵.论单光子研究[J].中国传媒大学学报(自然科学版)，2007，14(4)：1-9.

[22]佘卫龙.光的本性问题[A].1000个科学难题[C].北京：科学出版社，2009，328-332.

[23]Chown M.Einstein’ s Rio requiem[J].New Scientist，2004，(Mar 6)：50-51.

[24]Einstein A.The advent of the quantum theory[J].Scientist，1951，113：82.

[25]Einstein A.50年思考还不能回答光量子是什么[A].范岱年，赵中立，许良英，译.爱因斯坦文集(第2卷)[C].北京：商务印书馆，1977.

[26]Chown M.Quantum rebel[J].New Scientist，2004，(Jul 24)：30-35.

[27]Chown M.Quantum rebel wins over doubters[J].New Scientist，2007(Feb.17)：13.

[28]McKeever J.Deterministic generation of single photon from one atom trapped in a cavity[J].Science，2004，303：1992-1994.

[29]Kurtsiefer C，Mayer S.Stable solid-state source of single photon[J].Phys Rev Lett，2000，85：290-293.

[30]Moreau E.Single mode solid-state single photon source based on isolated quantum dots in pillar microcavities[J].Appl Rev Lett，2001，79：2865-2867.

[31]Santori C.Indistinguishable photons from a single photon device[J].Nature，2002.419：594-597.

[32]Keller M.Continuous generation of single photon with controlled waveform in an iontrap cavity system[J].Nature，2004，431：1075-1078.

[33]卢苏燕.法科学家成功追踪光子活动[N].科学时报，2007-03-15.

[34]Editoril.Speed of light computing，one photon at a time [J].New Scientist，2007，(July 21)：28.

[35]Heisenberg W.Uber den anschaulichen inhalt der quanten theoretischen kinematik und mechanik[J].Zeit für Phys，1927，43：172-178.

[36]黄志洵.负波速研究进展[J].前沿科学，2012，6(4)：46-65.

[37]黄宏嘉.现代微波理论与技术的发展[C].中国电子学会文集：微波理论与技术.北京：科学出版社，1980.

[38]中国物理学会.中国大百科全书(物理学)[M].北京：中国大百科全书出版社，2009.

[39]宋文淼.矢量偏微分算子[M].北京：科学出版社，1999.

[40]宋文淼，等.实物与暗物的数理逻辑[M].北京：科学出版社，2006.

[41]黄志洵.H11模截止衰减器的误差分析[J].电子学报，1963，1(4)：128-141.

[42]朱敏，黄志洵.金属壁内生成氧化层对高精密圆截止波导传播常数的影响[J].凯山计量，1984，(1)：1-12.

[43]Huang Z X(黄志洵)，Zeng C(曾诚).The general characteristic equation of circular waveguides and it’s solution[J].中国科学技术大学学报，1991，21(1)：70-77.

[44]黄志洵，徐诚.用介质片加载时矩形波导内的场分布[J].中国传媒大学学报(自然科学版)，2007，14(2)：1-9.

[45]Huang Z X(黄志洵).Zeng C(曾诚).Attenuation properties of normal modes in coated circular waveguides with imperfectly conducting walls[J].Microwave and Opt Tech Lett，1993，6(6)：342-349.

[46]黄忠洵.截止波导理论导论(第二版)[M].北京：中国计量出版社，1991.

[47]黄忠洵.论消失态[J].中国传媒大学学报(自然科学版)，2008，15(3)：1-19.

[48]黄志洵，孙金海.消失模波导滤波器的设计理论与实验[J].中国传媒大学学报(自然科学版)，2006，13(3)：1-8.

[49]黄志洵.消失态与Goos-Hänchen位移研究[J].中国传媒大学学报(自然科学版)，2009，16(3)：1-14.

[50]黄志洵.消失场能量关系及WKBJ分析法[J].中国传媒大学学报(自然科学版)，2011，18(3)：1-17.

[51]黄志洵.截止下圆波导衰减常数的精确公式[J].无线电计量，1975，(2)：13-20.

[52]Huang Z X(黄志洵)，Pan Z(潘津).Exact calculations to the propagation constants of circular WBCO[J].Acta Metrologica Sinica，1987，8(4)：267-270.

[53]黄志洵，马晓庆，郭允晟.美国Narda 8801横电磁波传输室性能的测量[J].电子工业标准化通讯，1983，(5)：21-26.

[54]Huang Z X(黄志洵)，Li T S(李天舒)，Yang Q S(杨青山).A new TEM transmission cell using exponential curved taper transition[J].Acta Metrologica Sinica，1992，13(2)：127-138.

[55]黄志洵，冀建军.吉赫横电磁室的实验研究[J].北京广播学院学报(自然科学版)，1994，(3)：48-56.

[56]黄志洵，赵爱军，贺涛.GTEM室内场强分布的计算分析[J].计量学报，1997，18(1)：63-71.

[57]黄志洵，冀建军.用于BP机测试的小型横电磁传输室[J].北京广播学院学报(自然科学版)，1999，(1)：8-14.

[58]黄志洵.超光速研究——相对论、量子力学、电子学与信息理论的交汇点[M].北京：科学出版社，1999.

[59]黄志洵.超光速研究新进展[M].北京：国防工业出版社，2002.

[60]黄志洵.电磁波经典波速理论及存在问题[J].北京广播学院学报(自然科学)，2004，11(2)：1-11.

[61]黄志洵.超光速研究理论与实验[M].北京：科学出版社，2005.

[62]黄志洵.超光速研究及电子学探索[M].北京：国防工业出版社，2008.

[63]黄志洵.超光速实验的一个新方案[J].前沿科学，2010，4(3)：41-62.

[64]黄志洵.论Bessel波速超光速现象[J].中国传媒大学学报(自然科学版)，2013，20(5)：1-14.

[65]黄志洵.自由空间中近区场的类消失态超光速现象[J].中国传媒大学学报(自然科学版)，2013，20(2)：40-51.

[66]黄志洵.波导截止现象的量子类比[J].电子科学学刊，1985，7(3)：232-237.

[67]黄志洵.超光速研究的量子力学基础[J].中国工程科学，2004，6(4)：15-25.

[68]Huang Z X(黄志洵)，Lu G Z(逯贵祯)，Guan J(关健).Superlurninal and negmive group velocity in the electromagnetic wave propagation[J].Eng Sci，2003，1(2)：35-39.

[69]黄志洵.负波速研究进展[M].前沿科学.2012，6(4)：46-65.

[70]黄志洵.无源媒质中电磁波的异常传播[J].中国传媒大学学报(自然科学版)，2013，20(1)：4-20.

[71]黄志洵.电磁波负性运动与媒质负电磁参数的研究[J].中国传媒大学学报(自然科学版)，2013，(4)：1-15.

[72]黄志洵.微波异常传播中的负折射率问题[J].物理，2001，30(11)：689-692.

[73]黄志洵.负折射率研究中的若干理论问题[J].北京广播学院学报(自然科学版)，2005，12(4)：1-11.

[74]黄志洵.超光速问题与电磁波异常传播[J].中国工程科学，2000，2 (10)：80-92.

[75]黄志洵.论量子超光速性[J].2012，19 (3)：1-28；19 (4)：1-17.

[76]范洪义.从量子力学到量子光学[M].上海：上海交通大学出版社，2005.

[77]Zajonc A.Light reconsidered[C].Opt & Photon，New Trends，2003，3(1)：S2.