连续型目标信息系统的属性约简

王秀秀, 王阿岩, 王长忠(渤海大学 数理学院, 辽宁 锦州 121000)



连续型目标信息系统的属性约简

王秀秀, 王阿岩, 王长忠
(渤海大学 数理学院, 辽宁 锦州 121000)

针对连续型数据的属性约简问题, 提出了一种新的属性约简方法----基于分配可辨识矩阵的属性约简方法。给出了基于连续型数据的分配协调集的概念, 研究了基于连续型数据的分配协调集的基本性质, 定义了基于分配协调集的辨识矩阵。在此基础上提出了基于辨识矩阵的连续型数据的属性约简方法, 并给出了计算辨识矩阵的算法。实例分析表明, 该方法能有效地对连续型数据进行属性约简。

粗糙集； 辨识矩阵； 属性约简； 连续值域信息系统

0 引 言

粗糙集理论[1,2]是由波兰数学家Pawlak[3]于1982年提出的一种数据分析理论, 目前已发展成为一种处理模糊和不确定性知识的数学工具。近年来, 被广泛应用于人工智能[4,5]、 过程控制、 数据挖掘[6,7]、 决策支持和分析以及知识发现[8]等领域。利用粗糙集进行数据挖掘、 知识规则[9,10]和特征选择[11-13]是基于粗糙集的属性约简理论[14,15]进行的, 属性约简是粗糙集理论的重要研究内容之一。

传统的粗糙集理论是基于论域上的等价关系描述的, 由等价关系形成划分, 构造论域上的上、 下近似算子, 并研究相应的知识约简与知识获取问题。 但这只适用于离散型的数据, 对于连续型目标信息系统, 对象之间的等价关系很难构造, 或对象之间本质上没有等价关系。笔者通过构造样本之间的一种相似关系对整个样本集进行粒化, 从而得到每个样本的相似类, 然后定义上、 下近似算子[16]以及分配协调函数, 研究连续型目标信息系统的辨识矩阵以及基于辨识矩阵的属性约简。

1 连续型数据的粗糙集

定义1[16]设(U,A,F,d,G)为一个目标信息系统, 其中U是非空有限样本集,U={x1,x2,…,xn}；A是条件属性集,A={a1,a2,…,am}；d是目标属性；F是U与A的关系集,F={fk:U→Vk,k≤m},Vk是连续型数据, 是ak的值域；G是U与d的关系集,G={gd:U→Vd},Vd={1,2,3,…,r}。则称(U,A,F,d,G)为连续型目标信息系统。

设(U,A,F,d,G)是连续型目标信息系统,ε∈[0,1]。对于B⊆A, 令

RB={(x,y)∈U×U: |fk(x)-fk(y)|≤ε, ∀ak∈B}

δB(x)={y∈U: (x,y)∈RB}

Rd={(x,y)∈U×U:gd(x)=gd(y), ∀ak∈B}

显然,RB是自反和对称的, 传递性则一般不成立, 所以RB是相似关系。ε是刻画样本相似性所允许的误差。Rd显然是论域上的等价关系, 从而产生论域上的一个划分, 即U/Rd={D1,D2,…,Dr}, 其中Di={x:gd(x)=i,x∈U}。

定义2[16]设(U,A,F,d,G)为连续型目标信息系统, 对于∀X⊆U, 在关系RB下的上、 下可近似定义为

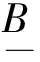
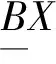
2 分配函数的概念及其性质

性质1 设(U,A,F,d,G)为连续型目标信息系统, 给定ε≥0, 设B⊆A, 则PosB(D)⊆PosA(D)。

定义3 设(U,A,F,d,G)为连续型目标信息系统, 给定ε≥0, 对于B⊆A, 记φB(x)={Dl:Dl∩δB(x)≠Ø}, 称φB(x)为相关决策类函数。若∀x∈U,φB(x)=φA(x), 则B是ε分配协调集。当B是ε分配协调集, 且∀C⊆B, ∃x0使φA(x0)≠φc(x0), 则B为ε分配约简。

性质2 设(U,A,F,d,G)为连续型目标信息系统, 给定ε≥0, 当B⊆A时, 则φA(x)⊆φB(x)(∀x∈U)。

证明 因为B⊆A, 所以RA⊆RB, 即∀x∈U,δA(x)⊆δB(x)。因为φB(x)={Dl:Dl∩δB(x)≠Ø}, 所以φA(x)⊆φB(x)。

3 连续型目标信息系统的辨识矩阵以及属性约简

定理1 设(U,A,F,d,G)为连续型目标信息系统,B⊆A, 若B是ε分配协调集, 当且仅当∀x,y∈U, 当gd(y)∉φA(x)时有y∉δB(x)。

证明1 充分性。∀x,y∈U, 若y∈δB(x), 则gd(y)∈φB(x)。因为B是ε分配协调集, 所以φB(x)=φA(x), 从而gd(y)∈φA(x), 得证。

证明2 必要性。∀x∈U, 若Dj∈φB(x), 则δB(x)∩Dj≠Ø, 所以∃y∈δB(x)使gd(y)=Dj。若y∈δB(x), 则gd(y)∈φB(x), 即Dj∈φA(x), 所以φB(x)⊆φA(x)。 因为B⊆A, 所以φA(x)⊆φB(x), 从而φA(x)=φB(x)。

定义4 设(U,A,F,d,G)为连续型目标信息系统。若∀x∈U, |φA(x)|=1, 则称(U,A,F,d,G)为一致连续型目标信息系统。

定理2 设(U,A,F,d,G)为连续型目标信息系统,B⊆A。则PosA(D)=PosB(D)当且仅当∀x∈U, 当|φA(x)|=1时, 有|φB(x)|=1。

证明 略。

定义5 设(U,A,F,d,G)为连续型目标信息系统, ∀x,y∈U, 定义

称E(x,y)为ε分配可辨识矩阵。

定理3 设(U,A,F,d,G)为连续型目标信息系统,B⊆A。B是约简当且仅当∀x,y∈U,B满足

B∩E(x,y)≠Ø, ∀b∈B, {B-b}∩E(x,y)=Ø。

基于分配协调集的辨识矩阵算法如下。

Input： 数据库系统D=(U,A,F)以及参数ε//ε是样本相似时所允许的误差。

Output：E//E是辨识矩阵。

1) 将样本集进行归一化处理。

2) 计算样本的个数row, 条件属性个数col。

3) 求d//d是个数组是样本的决策形成的等价类。

4) 求h//h是个数组, 每个细胞数组表示一个样本的相似类。

5) 求Q//Q是个数组, 每个细胞数组表示一个样本的相关决策类。

6)E={}；

7) fori=1:row

forj=1:row

ifgd(xj)∈Q(xi)//Q(xi)表示xi的相关决策类。

E{i,j}=1:col

Else

nosimilei={k∈A: |fk(xi)-fk(xj)|>ε}//k表示第k个条件属性。

E{i,j}=nosimiler

End

End

End

定义6 设(U,A,F,d,G)为连续型目标信息系统, 定义基于辨识矩阵的辨识公式

M=∧{∨{ai:ai∈E(x,y)}:x,y∈U}。

辨识公式M的最小表达式为

则M最小表达式的每一项为连续型目标信息系统的约简。

4 实例分析

表1是石油勘探信息表, 其中No为石油井编号,a1为平均振幅,a2为能量半衰减时间,a3为瞬时频率,a4为均方根振幅,d为决策。

表1 石油信息表Tab.1 The information of petroleum

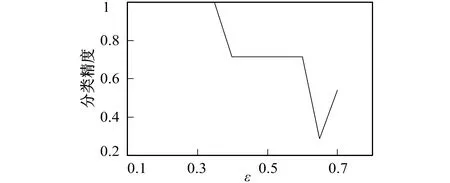
图1 分类精度Fig.1 Accuracy of selected features

笔者采用Matlab实现对笔者算法有效性进行检验, 实验结果如图1所示。

从图1明显可以看出, 当ε∈[0.1,0.35]时精度最高, 可以达到100%, 所以笔者的算法是有效的。例如, 当ε=0.3时, 分类精度是100%, 应用上述求辨识矩阵算法可得： 在ε=0.3时表1的辨识矩阵如表2所示。

表2 表1的辩识矩阵Tab.2 Discernibility matrix of table1

根据辨识公式

M=∧{∨{ai:ai∈E(xi,xj)}:i,j≤7}=∧{∨(E(xi,xj)):i,j≤7}=(a2∨a3)∧(a1∨a2∨a3)∧(a1∨a2∨a3∨a4)∧a2∧(a1∨a2∨a4)∧(a2∨a3∨a4)=a2

表1在参数ε=0.3的情况下, 属性{a1,a2,a3,a4}的约简是{a2}, 即在保持样本相关决策类不变的情况下, 属性可约简为{a2}。

5 结 语

笔者根据基于辨识矩阵的符号型信息系统的属性约简方法提出了基于辨识矩阵的连续型数据的属性约简方法, 并通过实例测试了方法的有效性。实例分析说明了方法能有效地对连续型数据进行属性约简。由于连续型数据的属性约简方法比较匮乏, 以后笔者还可以就变精度连续型数据的属性约简以及变精度优势关系下的属性约简进行研究。

[1]BONIKOWSKI Z, BRYNIARSKI E, WYBRANIEC U. Extensions and Intentions in the Rough Set Theory [J]. Information Sciences, 1998, 107: 149-167.

[3]PAWLAK Z, SKOWRON A. Rudiments of Rough Sets [J]. Information Sciences, 2007, 177: 3-27.

[4]WITOLD PEDRYCZ, SONG Mingli. Analytic Hierarchy Process(AHP) in Group Decision Making and Its Optimization with an Allocation of Information Granularity [J]. IEEE Transactions on Fuzzy System, 2011, 19(3): 527-539.

[5]任海军, 张晓星, 肖波, 等. 基于概念格的神经网络日最大负荷预测输入参数选择 [J]. 吉林大学学报: 理学版, 2011, 49(1): 87-93. REN Haijun, ZHANG Xiaoxing, XIAO Bo, et al. Input Parameters Selection in Neural Network Load Forecasting Made Based on Concept Lattice [J]. Journal of Jilin University: Science Edition, 2011, 49(1): 87-93.

[6]YAO Yiyu, ZHAO Liquan. A Measurement Theory View on the Granularity of Partitions [J]. Information Sciences, 2012, 213: 1-13.

[7]WANG Changzhong, CHEN Degang, SUN Baiqing, et al. Communication between Information Systems with Covering Based Rough Sets [J]. Information Scienceset, 2012, 216: 17-33.

[8]SWINIARSKI R W, SKOWRON A. Rough Set Methods in Feature Selection and Recognition [J]. Pattern Recognition Letters, 2003, 24(6): 833-849.

[9]BLASZCZYNSKI J, SLOWINSKI R, SZELAG M. Sequential Covering Rule Induction Algorithm for Variable Consistency Rough Set Approaches [J]. Information Sciences, 2011, 181(5): 987-1002.

[10]DU Y. Rule Learning for Classification Based on Neighborhood Covering Reduction [J]. Information Science, 2011, 181(5): 5457-5467.

[11]杨杰明, 刘元宁, 曲朝阳, 等. 文本分类中基于综合度量的特征选择方法 [J]. 吉林大学学报: 理学版, 2013, 51(5): 887-893. YANG Jieming, LIU Yuanning, QU Chaoyang, et al. Feature Selection Algorithm Based on Comprehensive Measurement for Text Categorization [J]. Journal of Jilin University: Science Edition, 2013, 51(5): 887-893.

[12]鲍捷, 杨明, 何志芬. 基于SVM评价准则的高维数据混合特征选择算法 [J]. 吉林大学学报： 理学版, 2012, 50(6): 1192-1198. BAO Jie, YANG Ming, HE Zhifen. Ensemble Feature Selection Algorithm Based on SVM-Based Criteria for High-Dimensional Data [J]. Journal of Jilin University: Science Edition, 2012, 50(6): 1192-1198.

[13]JENSEN R, SHEN Q. New Approaches to Fuzzy-Rough Feature Selection [J]. IEEE Transactions on Fuzzy Systems, 2009, 17(4): 824-838.

[14]WU W Z. Attribute Reduction Based on Evidence Theory in Incomplete Decision Systems [J]. Information Sciences, 2008, 178: 1355-1371.

[15]MAJI P, GARAI P. Fuzzy-Rough Simultaneous Attribute Selection and Feature Extraction Algorithm [J]. IEEE Transactions on Cybernetic, 2013, 43(4): 1166-1177.

[16]张文修, 梁怡, 吴伟志. 信息系统与知识发现 [M]. 北京： 科学出版社, 2003. ZHANG Wenxiu, LIANG Yi, WU Weizhi. Information System and Knowledge Discovery [M]. Beijing: Science Press, 2003.

(责任编辑： 张洁)

Attribute Reduction in Numerical Decision Systems

WANG Xiuxiu, WANG Ayan, WANG Changzhong
(College of Mathematics and Physics, Bohai University, Jinzhou 121000, China)

A method which aims at attribute reduction based on assignment set in numerical data sets is proposed. Firstly, the concept and some important properties of assignment set based on numerical data sets was presented. Then, authors defined dicernibility matrix based on assignment set, and proposed a new method for attribute reduction based on discernibility matrix in numerical data sets. Finally, an algorithm for computing discernibility matrix was presented. Example analysis show that this method can effectively handle attribute reduction in numerical decision systems.

rough sets； discernibility matrix； attribute reduction； numerical decision systems

1671-5896(2014)05-0534-05

2013-11-13

国家自然科学基金资助项目(61070242); 辽宁省优秀人才支持计划基金资助项目(LR2012039)

王秀秀(1988— ), 女, 辽宁庄河人, 渤海大学硕士研究生, 主要从事粒计算与模式识别理论与方法研究, (Tel)86-15241622803(E-mail)wangxiuxiujiayou@126.com； 王长忠(1968— ), 男, 内蒙古商都人, 渤海大学副教授, 博士, 硕士生导师, 主要从事粒计算、 模式识别和数据挖掘研究, (Tel)86-15041656439(E-mail)changzhongwang@126.com。

TP18

： A