基于前馈补偿的球磨机系统多变量解耦PI控制

薛美盛，胡岸，薛生辉，任俊超

(中国科学技术大学 自动化系，合肥 230026)

PID控制器在工业控制领域取得了广泛的应用，一方面它使用简单、容易操作，另一方面是由于它对于绝大多数工业对象都能够提供良好的控制性能。当控制要求较高时，可以组合额外的控制方案显著地提高控制性能(设定点权重、前馈控制等)。然而，这些方案大多都是针对单输入单输出(SISO)系统[1]。对于钢球磨煤机等一类多变量、大时滞的工业控制对象，要复现上述方案会比较困难。以往的控制系统常常以手动控制为主[2]。文献[3]将鲁棒整定的PID引入了球磨机控制中并取得了较好的控制效果，但由于未加入解耦环节，两个回路间的耦合较严重，使得该方法仍有一定的局限性。

对于球磨机存在耦合的温度和负压回路，用热风量控制球磨机出口温度，再用循环风量控制其入口温度可得到双输入双输出(TITO)控制系统。针对该特性，笔者首先设计解耦环节来实现完全解耦，再根据稳态裕量模型简化法将开环传递函数H(s)中元素降阶为一阶加纯滞后(FOPFT)形式。然后，根据简化模型设计出前馈补偿环节并整定PI参数。最后将本文提出的方法与现有方法进行仿真对比验证有效性。

1 解耦环节设计

解耦环节应该满足如下的要求[4]： 开环传递函数PD应该为对角形；不具有高通滤波特性；应该尽可能少地含有动态特性和时滞环节；应该能够满足自动控制系统的一些特殊要求。

带有纯滞后的TITO系统传递函数矩阵形式如下：

(1)

式中：pi j(s)=ki jpo i j(s)e-θi js，其中i，j=1， 2;po i j(s)——无滞后、正则且稳定的传递函数；ki j——稳态增益。解耦矩阵可以表示为如下形式：

(2)

那么解耦后的开环传递函数可以表示为

(3)

如果令副对角线上元素为0，系统可以被等效地转化为2个SISO系统，从而输入到输出可以实现完全解耦。由上面逻辑得到方程组：

(4)

(5)

为便于物理实现，解耦矩阵的所有元素不能含有超前项，可对矩阵元素配置如下：

(6)

(7)

为了获得期望的解耦目标函数，也可以利用下面的配置方法：

(8)

根据式(8)，可以确定出相应的解耦矩阵形式：

(9)

2 基于稳态裕度的模型简化规则

由于加入解耦矩阵后开环传递函数的形式如式(3)，具有比较复杂的动态特性，传统的PID整定原则无法使用，模型简化技术就显得比较重要。很多文献都提到过将复杂模型用FOPDT模型来近似[5]。虽然FOPDT模型不能体现复杂模型的所有特点，但是它在稳态增益、时间常数和过程等效时滞等方面对系统特性比较合理地进行描述。笔者将以上特点针对一些动态过程不是十分剧烈的被控对象，根据稳定裕度等频率特性，弱化过渡过程对系统的影响，提出一种近似的模型简化技术。

设化简前的传递函数为h(s)，化简后的FOPDT模型如下：

(10)

化简前系统的穿越频率为ωx，满足

∠h(jωx)=(2k+1)π

(11)

q(s)传递函数包含3个未知参数。利用简化前后方程的幅值裕度与穿越频率相同，在穿越频率处两者相角也相同，即得到3个方程：

(12)

对上述方程组进行计算，可以得到结论：

(13)

式中：h——穿越频率处的幅值裕度。注意： 有时由于传递函数的特殊性，无法获得穿越频率，需要利用截止频率ωc处的相角特性和幅值特性构建方程，其计算方法如下：

|h(jωc)|=1

(14)

q(s)传递函数同样包含3个未知参数，需要构建3个方程。利用简化前后的相角裕度相同，并且在截止频率处相角也相同，即可得到如下方程组：

(15)

式中：γ——h(s)的相角裕度。

为了验证上述化简方法，将Wood-Berry[6]蒸馏塔模型解耦后获得的广义开环传递函数对角元素如下：

为了使用下文中的PI控制器，应该将h1(s)和h2(s)化简成为FOPDT的形式，利用上述方法得到化简后的对象表达式为

通过对简化前后的h(s)和q(s)的阶跃响应曲线进行对比，发现该简化方法较好地复现了原函数的特性，如图1所示。

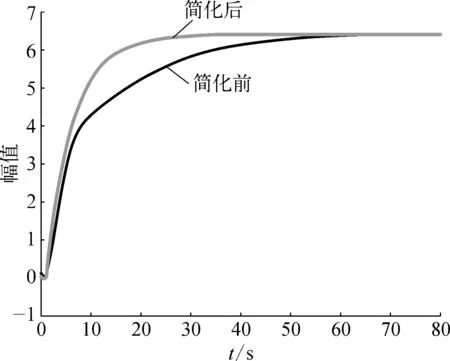
a) h1(s)与q1(s)的阶跃响应曲线

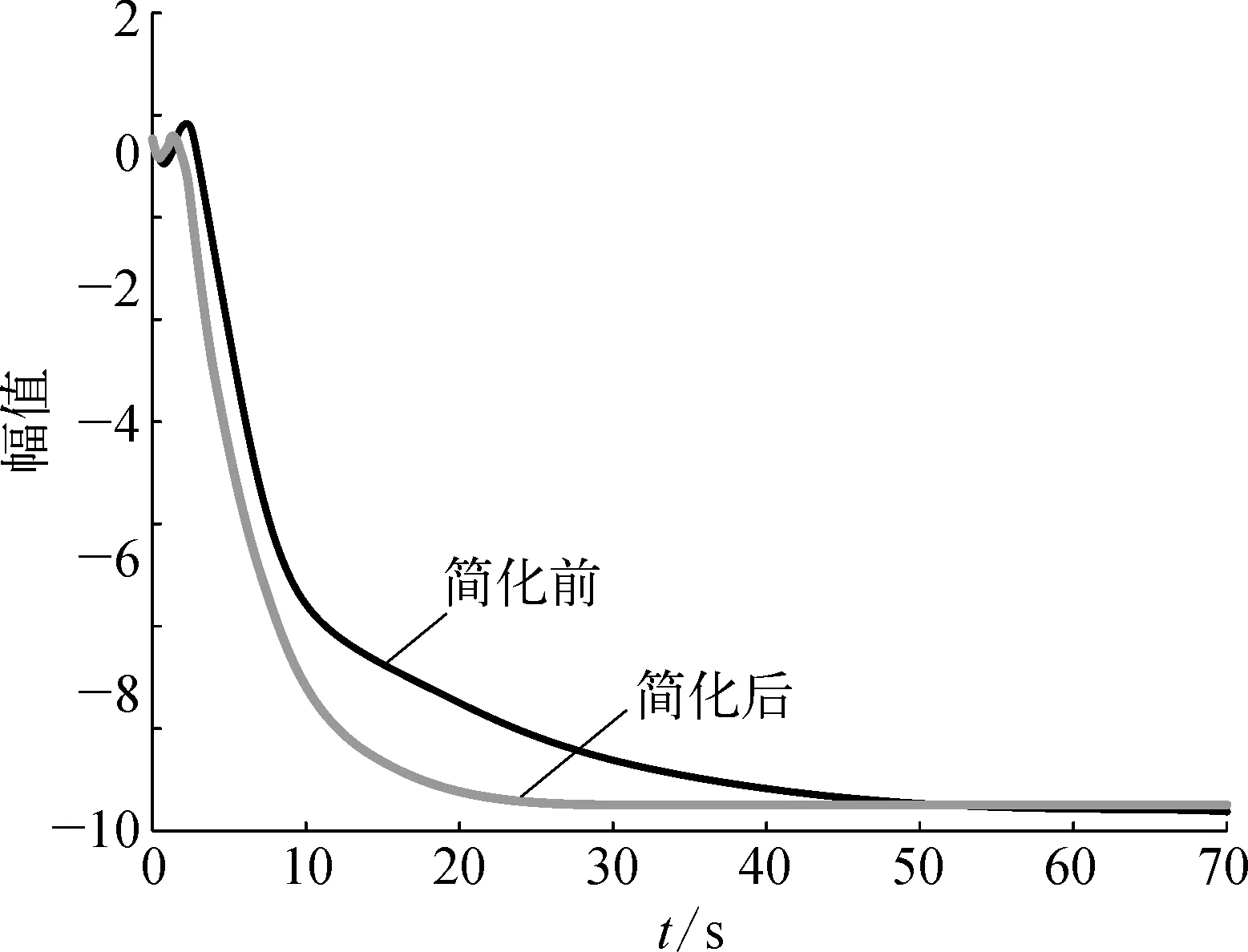
b) h2(s)与q2(s)的阶跃响应曲线

3 前馈补偿环节和PI控制器设计

3.1 前馈补偿环节

前馈补偿环节能够提高系统的设定点跟踪性能，针对SISO系统已有很多成功的应用，如设定点权重[7]、Bang-Bang控制[8]等。然而，如何应用到如球磨机等TITO对象还没被太多的研究过，笔者将从这一点出发对其进行探索。SISO对象的前馈补偿加PID环节的控制结构如图2所示。

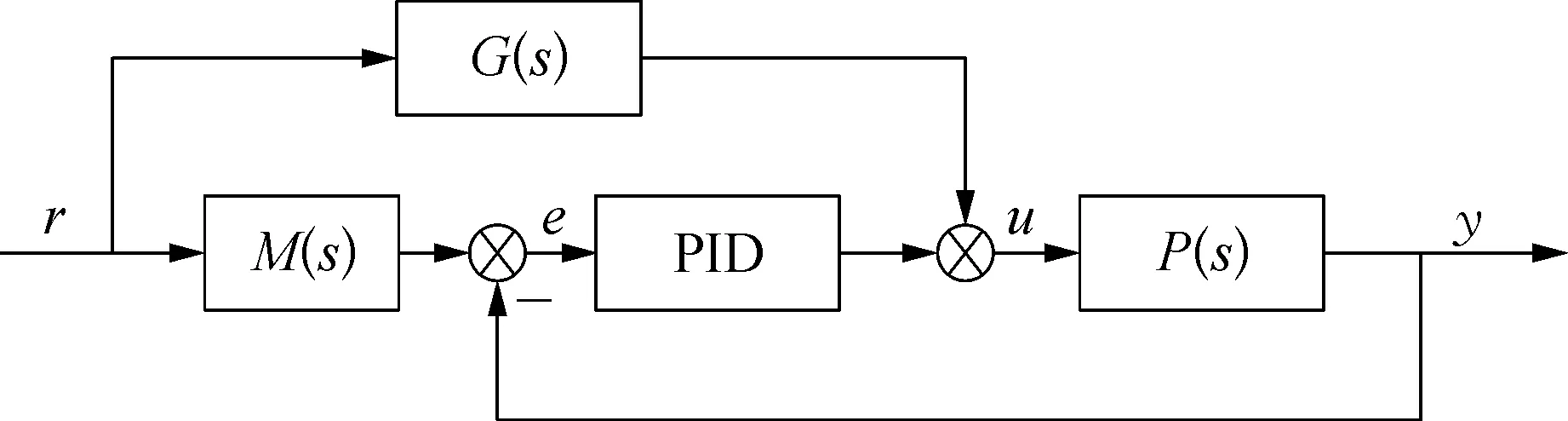
图2 针对SISO对象的前馈补偿加PID环节的控制结构示意

令M(s)为参考模型，用于确定系统对于设定点变化的期望响应，并且应该包含被控对象传递函数P(s)的非最小相位环节。由于M(s)与P(s)的阶次相同，从而可以确定出G(s)的形式：

(16)

使用该种补偿方法，前馈补偿器包含了一个对象模型和超前滞后网络[9]。如果M(s)的时滞小于P(s)时，该方法并不能够直接应用到多输入多输出(MIMO)环节，甚至是TITO环节。因为前馈环节会出现纯超前的形式，无法物理实现。

设经过解耦并化简后的模型为FOPDT形式，有以下模型简化方法：

(17)

根据解耦后对象的输出响应的特点，同时为了确保方案的可实现性，将参考模型的形式设定为如下形式：

(18)

在实际对系统快速性要求比较高而执行器性能较好的控制场合，也可以根据需要将上式的纯滞后环节去掉，进而使得响应过程更迅速。因此可以得到：

(19)

3.2 PI整定规则

为便于在DCS使用，对于球磨机采用PI控制器：

(20)

对于PI控制器参数的选择，可以使用Hagglund[1]使用的IAE整定规则，即

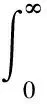
(21)

式中：e(t)——系统的控制误差。根据Visioli[10]提出的ITAE指标，使得下面目标函数(i=1， 2)：

(22)

最小的情况下选取相应的参数KC，TI。在计算准确的情况下，上述方法均可获得良好控制效果。在工业条件下，为了在方便地整定参数的同时获得良好的控制效果，笔者在查阅相关PID参数整定文献后，做了大量仿真实验，确定出专门针对球磨机的参数整定公式：

(23)

TI=Tm

(24)

4 仿 真

下面通过文献[3]中提出的球磨机的模型来对上述控制效果进行分析和验证。

通过分析，被控对象输出之间存在较大的耦合作用和明显时滞，采用传统方法无法对其进行较好地控制。由前述的解耦规则得到解耦矩阵：

解耦后的开环传递函数：

从对角元素的表达式可以看出传统的PID整定规则无法使用，应先使用模型降阶技术将其简化为FOPDT形式，再使用文中整定规则。穿越频率ω11X=0.8935，ω22X=7.782K11=0.803，T11=5，τ11=2；K22=20.8，T22=5.17，τ22=1.2。

注意： 在实际应用中得到的近似参数可能不会很好地匹配原来的对象模型，从而可对其作出一些调整，以达到满意的效果，这里将τ22的取值调整为2。化简后的模型传递函数为

化简前后模型对阶跃输入的响应曲线如图3所示。除了存在较小的稳态误差外，模型t11能够很好地复现复杂传递函数H11的响应特性，而H22的阶跃响应特性可以被t22近似完全复现。由此，模型化简方法可以得到很好的效果。

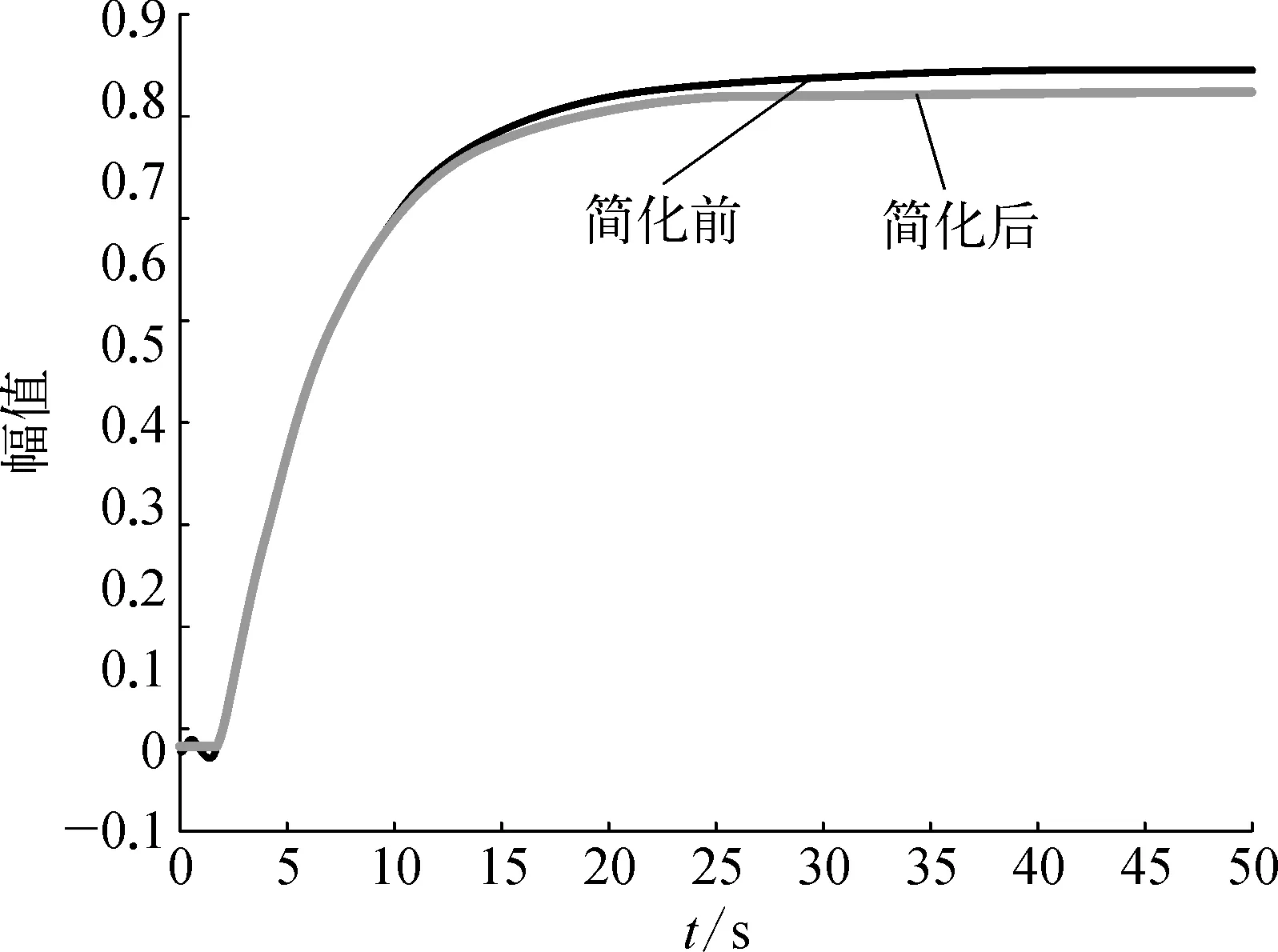
a) H11简化前后的阶跃响应曲线对比

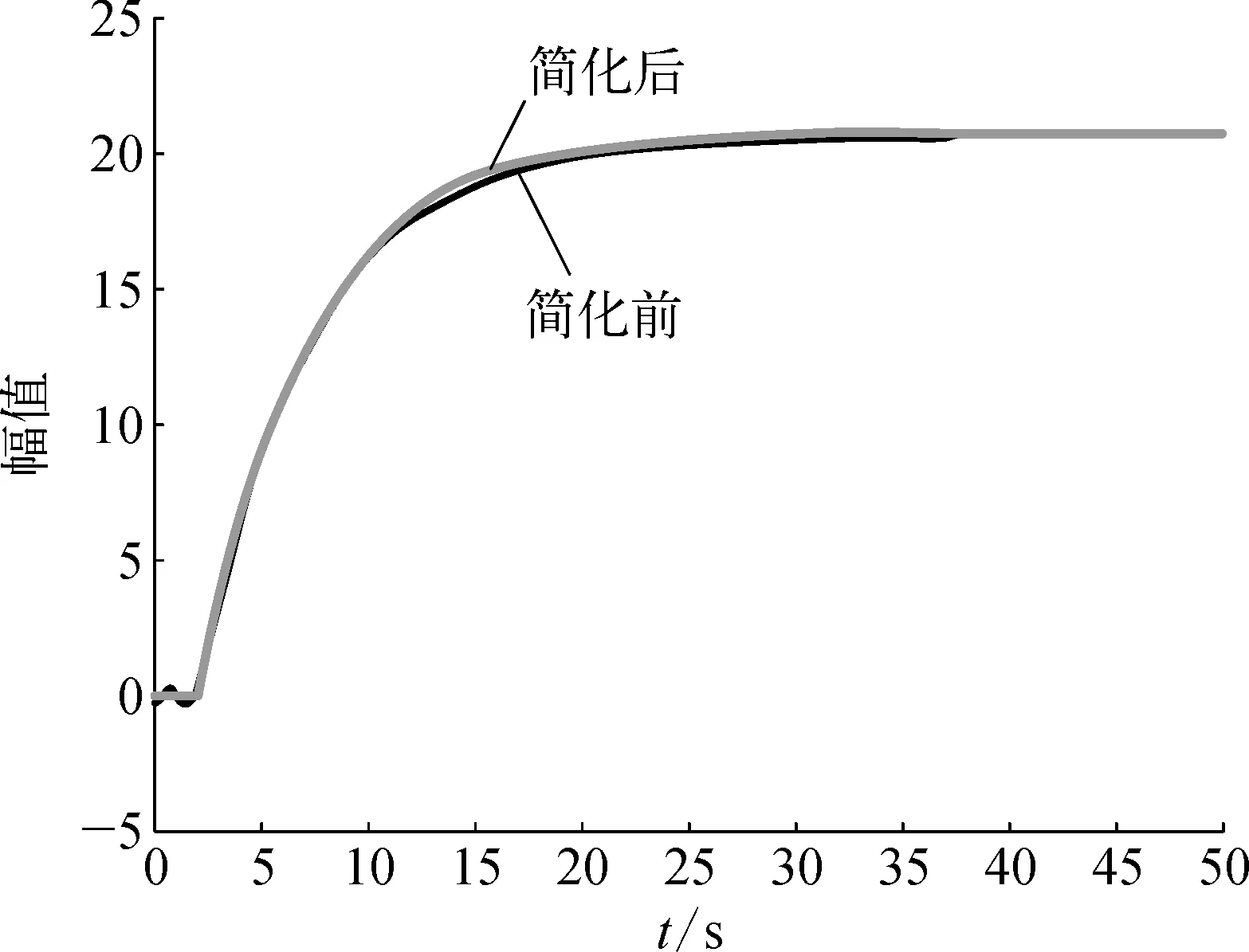
b) H22简化前后的阶跃响应曲线对比

由文中PI整定规则，控制器C11(s)，C22(s)的相关参数选取：KP11=1.037，TI11=5，KP22=0.0414，TI22=5.17。

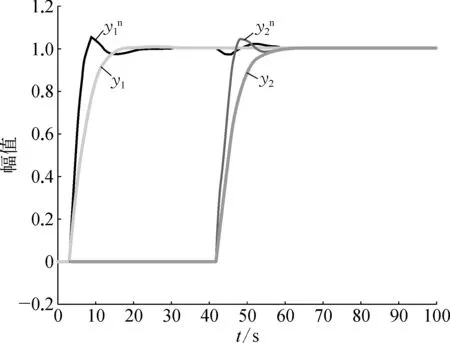
图4 无前馈环节的控制效果与文献[3]整定方法的对比曲线

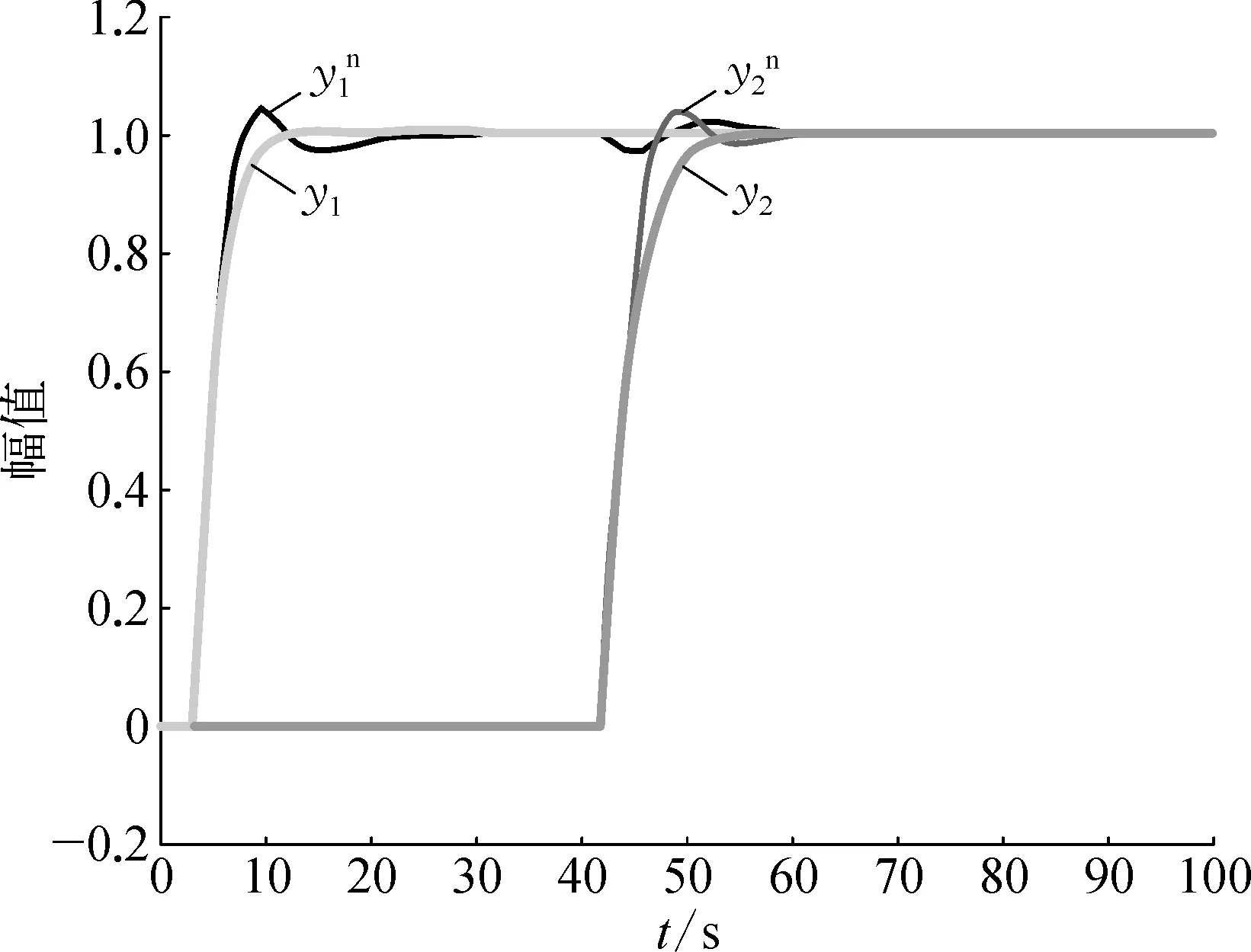
图5 加入前馈环节后与文献[3]整定方法对比

从图5中看到，加入前馈环节后系统仍无超调，响应速度迅速提高，并且阶跃响应曲线十分光滑，设定点跟踪性能获得显著提升。图6为当发生意外，使得PID参数变化后(KP1=1.4，KP2=0.05)时对应的阶跃响应曲线。其中a)图中为加入前馈环节后的响应曲线，在PID参数失配时仍无超调，且响应速度比无前馈环节要快；b)图中无前馈环节，曲线发生明显的超调。

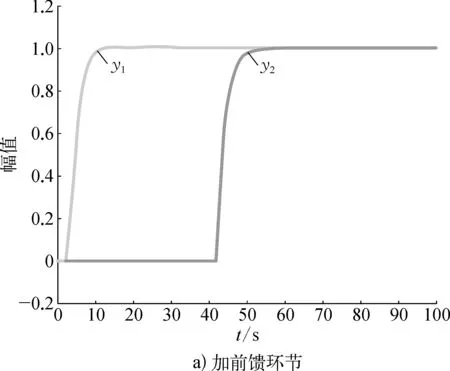
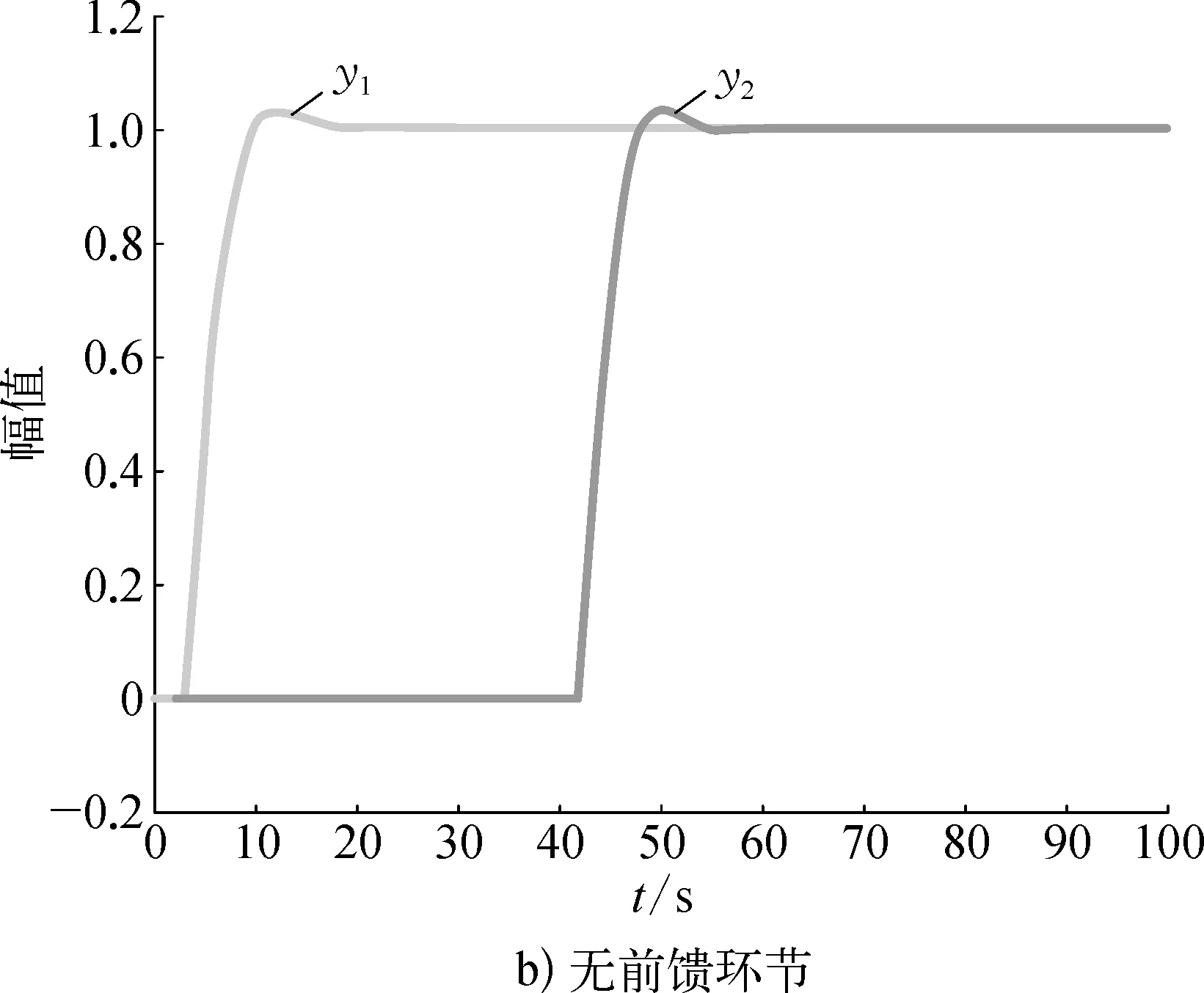
图6 控制器失配情况下系统阶跃输出响应曲线

5 结束语

文中提出了针对球磨机的前馈补偿环节，给出了一种有效的模型降阶方法，且提出的PI控制器整定规则简单。仿真结果表明，该方法具有良好的设定点跟踪性能，能够有效地消除输出间的耦合作用。

参考文献：

[1] ASTROM K J， HAGGLUND T. Advanced PID Control [M]. ISA， 2006.

[2] 王东风.钢球磨煤机制粉系统的优化控制[J].动力工程，2002，22(03)： 1793-1797.

[3] 綦守荣，王东风，韩璞，等.基于鲁棒整定的球磨机系统多变量PID控制[J].系统仿真学报，2005，17(12)： 3001-3003.

[4] NORDFELDT P， HGGLUND T. Decoupler and PID Controller Design of TITO Systems [J]. Journal of Process Control， 2006， 16(09)： 923-936.

[5] WANG Q G， HUANG B， GUO X. Auto-Tuning of TITO Decoupling Controllers from Step Tests [J]. ISA Transactions， 2000， 39(04)： 407-418.

[6] 靳其兵，袁琴.双输入双输出过程解耦内模控制[J].控制工程，2009，16(01)： 5-7.

[7] ARAKI M， TAGUCHI H. Two-Degree-of-Freedom PID Controllers [J]. International Journal of Control Automation and Systems， 2003(01)： 401-411.

[9] VISIOLI A. A New Design for a PID Plus Feedforward Controller [J]. Journal of Process Control， 2004， 14(04)： 457-463.

[10] VISIOLI A. Practical PID Control [M]. Springer， 2006.

[11] 王东风.制粉系统球磨机控制方法综述[J].河北电力技术，2001，20(02)： 10-13.

[12] 程启明，王勇浩.火电厂中间储仓式球磨机制粉系统控制技术发展综述[J].上海电力学院学报，2006，22(01)： 48-54.